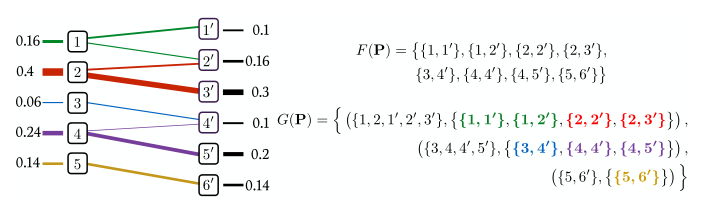Computational Optimal Transport 精読会 記録 (#8: 3.6)

背景

• 前回: Computational Optimal Transport 精読会 記録 (#7: 3.5)はGW前の4/23に開催，今回はGW後の5/8に開催
• 職場でCOTを読んでおり，{自己満足,復習,将来のため}などの理由で記録をしている

今回の範囲の内容

• 双対上昇法 (Dual Ascent Method)

アンチョコ

• Kantorovich problem: $L_C(\mathbf{a,b}) = \min_{\mathrm{P}\in U(\mathbf{a, b})} \langle C, P \rangle$, $U(a, b) = \{\mathrm{P}\in \mathbb{R}_+^{n\times m}\mid \mathrm{P} \mathbb{1}_m = \mathbf{a}, \mathbf{P}^T \mathbb{1}_n = \mathbf{b} \}$

• Dual problem $L_C(\mathbf{a,b}) = \max_{(\mathbf{f, g})\in R(C)} \langle \mathbf{f, a}\rangle + \langle \mathbf{g, b}\rangle$, $R(C) = \{(\mathbf{f,g})\in\mathbb{R}^n\times \mathbb{R}^m \mid \mathbf{f \oplus g} \leq C\}$

• $G({\bf P})$は輸送が存在する山の間に辺をはった二部グラフ

• complementary: もし${\bf P}_{i,j} > 0$ (輸送する)ならば，$C_{i,j} = {\bf f}_i + {\bf g}_j$であること

• feasible: $\mathbf{f} \oplus \mathbf{g} \leq \mathbf{C}$であること

§3.6 Dual Ascent Method

• ここではネットワークフローを用いた一般的なDual Ascent Methodのフレームワークについて説明する

• 歴史的には§3.5で学んだnetwork simplex法よりも古く，関連するアルゴリズムとして二部グラフマッチングなどで利用されているハンガリアン法がある

• 前回まで作成していた二部グラフを思い出す: Figure 3.3

• 送り元(左側)の頂点集合を$S$，送り先(右側)の頂点集合を$S'$で書き，それぞれ$\mathbf{1}_S, \mathbf{1}_{S'}$は集合ベクトル（集合の要素に対応する位置が1になっている0-1ベクトル）

• 前提

  • $\mathbf{f, g}$はfeasibleとする
  • $\mathbf{f}_i + \mathbf{g}_j = C_{i,j}$が既に成り立っている辺をbalancedと呼び，その集合を$\mathcal{B}$で表す
  • 成り立っていない辺をinactiveと呼ぶ

Prop 3.5

• やりたいこと

  • 現在の解 $\mathbf{f, g}$ を少しだけ変えた新しい解 $\mathbf{f',g'}$ を作り，より良い解が得られるようにしたい
  • 定義: $\mathbf{f}' = \mathbf{f} + \epsilon \mathbf{1}_{S}, \mathbf{g}' = \mathbf{g} - \epsilon \mathbf{1}_{S'}$
    • お互い$\epsilon$ずつズラすので，既にbalancedな辺については，balancedが崩れないようになっている
    • Prop 3.5の証明で等号を入れるべきでズレているところがあるっぽい

• 操作: 今inactiveなペアを考える

  • ある$i$に対して，inactiveな頂点先の集合を$\mathcal{I}_i$で表す
  • ある$i, j$がinactiveであるとき，$\epsilon_i = \min_{j\in I_i} C_{i,j} - \mathbf{f}_i - \mathbf{g}_j$ を定義する
    • これは最もinactive度合いが小さいペアを探してくる操作に対応

• 言いたいこと: balancedな$(i, j')$であるえば，$j'$は$S'$に含まれる

  • 補題1: よって$(i,j')$がbalanceではないとき，feasibleになることを示す（場合分け）
  • 補題2: balanceであるとき，$j'\in S'$のみを示す（場合分け）
  • 両方成り立つので，Prop3.5が成り立つ

• 操作の比較

  • network simplex
    • feasible primal solution $P$からはじまる
    • complementary feasible dual pair $(f, g)$を計算する
    • これをcomplementaryかつfeasibleであるように修正しながら進む
  • dual ascent method
    • feasible dual pair $(f, g)$からはじまる
    • これを修正できる$(f', g')$に変化させながら更新していく
    • 更新していくときの目的関数値の性質がProp 3.6

Prop 3.6

• $(f, g)$を$(f', g')$に更新したとき（ある性質を満たす$S$と$S'$が存在），目的関数値が良化する，もしくは最適値である
• 証明でネットワークフローを利用するが，使われているLabelingアルゴリズムがどういうものか明示されていないので想像になる（図も間違っているかもしれない）
• Labelingアルゴリズムで，フロー容量が飽和していないところを抽出でき，集合$S$と$S'$を得られるということになっている（不明）
• サチっているところ(balanced)とそれ以外に区別
• ここでフロー量(A, B, C, D)の釣り合いなどにより，主題が成り立つ
• このあたりは証明がテクニカルなのと外部参照なので，読んだときはわかった気になったけど，振り返ると難しいままな感じになっている（反省）
• Dual Ascent Methodの場合はextremal pointかどうかも関係ないので，少し性質が異なる
• ここの深い理解は課題…

次回

• 少し間があいて5/23に開催