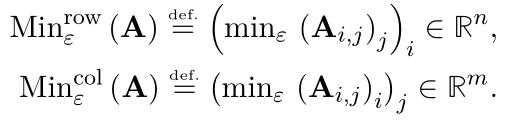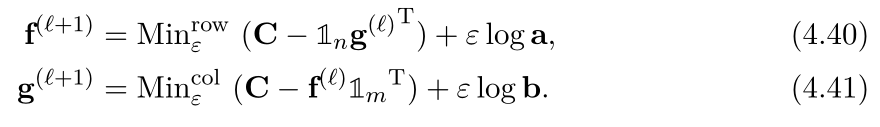背景
- 前回: Computational Optimal Transport 精読会 記録 (#15: 4.3 その2,4.4 その1)は7/16に開催,今回は7/26に開催
- 職場でCOTを読んでおり,{自己満足,復習,将来のため}などの理由で記録をしている
前回の振り返りと今回の内容
- エントロピー正則化付きの輸送問題
- $L^\varepsilon_C({\bf a}, {\bf b}) = \min_{{\bf P}\in U({\bf a},{\bf b})} \langle {\bf P}, C\rangle - \varepsilon H({\bf P})$
- Sinkhornアルゴリズム最高 → ちゃんと収束するし,高速化できるよ.安定化するためにはLogドメインが必須だよ.
- $\mathbf{u}^{(l+1)} = \frac{\mathbf{a}}{\mathbf{Kv}^{(l)}}$, $\mathbf{v}^{(l+1)} = \frac{\mathbf{b}}{\mathbf{K}^T\mathbf{u}^{(l + 1)}}$
- エントロピー正則化付きのdual問題
- $L_C^\varepsilon(a,b) = \max_{f, g} \langle f, a\rangle + \langle g, b\rangle - \varepsilon \langle \exp(f/\varepsilon), K\exp(g/\varepsilon)\rangle$
- 今回: 詳細を確認していく
Remark 4.21
- Sinkhornアルゴリズムは$u, v$を交互に更新していくので,これをblock coordinate ascentとして見てみよう
- それぞれ$f, g$について偏微分すると(4.33), (4.34)を得る
- (4.33) $\nabla|_f Q(f, g) = a - \exp(f/\varepsilon) \odot (K\exp(g/\varepsilon))$
- (4.34) $\nabla|_g Q(f, g) = b - \exp(g/\varepsilon) \odot (K^T \exp(f/\varepsilon))$
- $f$と$g$側をそれぞれcoordinateとみなして,交互に更新すると,(4.35), (4.36)を得る
- 例えば式(4.33)=0とした場合
- $a = \exp(f/\varepsilon) \odot K \exp (g / \varepsilon)$
- 両辺の対数を取って
- $\varepsilon \log a = f + \varepsilon \log (K\exp(g / \varepsilon))$
- $f$を更新する形の式にすると
- $f^{(l+1)} = \varepsilon a - \varepsilon \log (K\exp(g^{(l)} / \varepsilon))$ → 式(4.35)
Remark 4.22
- 更新式(4.35)と(4.36)はblock coordinate ascentとしても見ることができるが,soft-minimumとしても見ることができる
- soft-minの定義
$$\min_\varepsilon \mathbf{z} = -\varepsilon \log \sum_i \exp(-\mathbf{z}_i / \varepsilon)$$
-
目を薄めてみると,式(4.35), (4.36)の更新式はsoft-minをしていると考えられる
-
soft-minの記号($\min_\varepsilon$)で更新式を書き直す
- (4.35)を書き直した(4.38): $f^{(l+1)}) = \min_\varepsilon \{ (C_{ij} - \mathbf{g}_j^{(l)}) \} + \varepsilon \log a$
- ちょっと記号が怪しいかもしれない(添字)
- (4.35)を書き直した(4.38): $f^{(l+1)}) = \min_\varepsilon \{ (C_{ij} - \mathbf{g}_j^{(l)}) \} + \varepsilon \log a$
-
この操作を簡単に書くために2つのオペレータを定義
- これを用いて式(4.40), (4.41)のような更新式が得られる
- これはエントロピー正則化付きのC-変換みたいな操作になっている
- 実装的な話をすると,機械学習でよく出てくるlog-sum-expも使ってね
Next
- 式が多すぎてQiitaエディタ入力が面倒になった
- 次回は§4.5に沿って近似解法についてやっていく