Julia Advent Calendar 2017の記事です。JuliaはPython/Numpyは遅いけどC++書きたくないときや、Matlabで謎の行列計算プログラムがあるけどMatlab起動したくないときに代わりに使っています。データもなんとか読めますしね。過去記事の宣伝…。

Einsum.jlの概要

Python/Numpyで一部の層にニッチな受容があるnp.einsumというメソッドがあるのですが、それをJuliaでも使えるパッケージがEinsum.jlです。マクロで実装されています。例えば三次元ベクトル$A=(A_1, A_2, A_3)$と$B=(B_1, B_2, B_3)$について、その内積は$A\cdot B = A_1 B_1 + A_2 B_2 + A_3 B_3$と書けるわけですが、この「要素iについて演算して足す」に相当する部分をEinsum.jlが担います。例えば次のような記事を読んで頂ければ、どういうものなのかもう少し真面目に具体的に分かると思います。

アインシュタインの縮約表記 - 大人になってからの再学習

インストールは普通にやります。

Pkg.add("Einsum")

内積の計算にEinsumを使うと次のように書きます。Σの中身をそのまま書いているような雰囲気になります。

using Einsum.jl
A = randn(3);
B = randn(3);
AB = 0;
@einsum AB = A[i] * B[i] 
println(AB)         # Einsum.jlによる計算
println(dot(A, B))  # build-in functionによる計算

Pythonとの比較

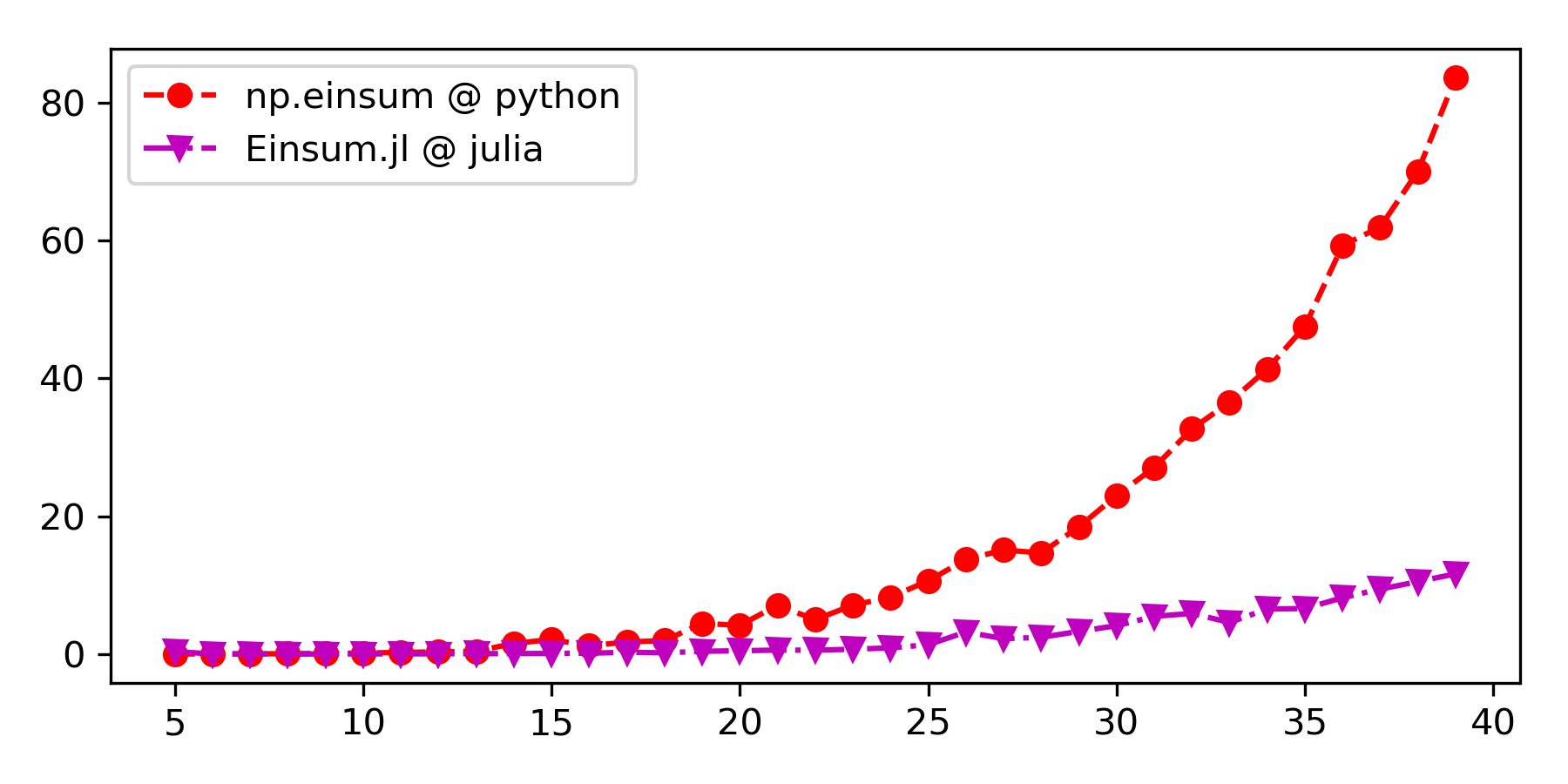
あまり真面目に比較するつもりはないですが（測定方法どうしたらいいか分からない・・・）、一応github上でベンチマーク用っぽいものを実行してみました。Pythonのnp.einsumは高次元だと遅いという噂がありますが、実際遅かったです。

using Einsum

function benchmark(;dim1=30, dim2=20)
    A = randn(dim1, dim2)
    B = randn(dim1, dim2)
    C = randn(dim1, dim2)
    D = randn(dim1, dim2)
    E = randn(dim1, dim2)
    X = zeros(dim2, dim2, dim2, dim2, dim2)
    @einsum X[a,b,c,d,e] = A[r,a] * B[r,b] * C[r,c] * D[r,d] * E[r,d]
end

Pythonとnumpyで同じ計算を実行した結果のグラフ。雰囲気だけお楽しみください。

実装詳細の話

最初に少し触れましたが、実装はマクロでされています。なぜマクロが必要なのかというと、Einsumの式が

X[a,b,c,d,e] = A[r,a] * B[r,b] * C[r,c] * D[r,d] * E[r,d]

のように、Juliaの式で渡されるからです。Python/Numpyでは、これをra,rb,rc,rd,rd->abcdeというような文字列で渡して実行しています。一方Juliaでは、この式がパースされたデータ構造Exprで渡ってきます。実際に行列積の場合を例に、Exprの中身を見てみると、なんとなくこれをパースしていけば、上のEinsum計算を実行するfor文に変換できそうですね（これをEinsum.jlがやってます）。余談ですが、与えられた行列（BやC）の型を見てAの型を決定するために、promote_typeやeltypeが使われています。Juliaerにしたら常識かもしれないですが、自分はこの関数たちは使ったことなかったです。

julia> expr = :(AB[i, k] = A[i, j] * B[j, k])
:(AB[i,k] = A[i,j] * B[j,k])

# 第一引数を見てみる
julia> expr1 = expr.args[1]

# dumpで中身を可視化 (xdumpはdeprecated)
julia> dump(expr1)
Expr
  head: Symbol ref
  args: Array{Any}((3,))
    1: Symbol AB
    2: Symbol i
    3: Symbol k
  typ: Any

# 実際にevalしてみる
julia> A = zeros(2, 2, 2); i = 1; j = 1; k = 1;

julia> eval(expr1)
0.0 # zeros(2, 2, 2)の[1, 1, 1]要素

オマケ

公式のgithubには特別書かれてないですが、左辺の行列インデクスに出てこない右辺の行列インデクスについて和を取るという仕組みが実装されていました。動作確認してみましょう。

A = zeros(2)
B = rand(2, 2)
C = rand(2, 2)
@einsum A[i] = B[i, j] * C[j, k]  # kが浮いている

これはCの行方向が浮いている状態なので、Cを行方向に和したベクトルで置き換えられます。つまり上のAは下のA2と同じ結果になります。

C2 = sum(C, 2)
@einsum A[i] = B[i, j] * C2[j]

まとめ

Einsum.jlの簡単な使い方を説明して、中身を少し読んでみました。300行程度の短いコードなので、1行ずつ読んでいってもなんとかなりますね。本題には関係ないですが、今回の記事の内容はGitbookで書きました。テンプレート環境などを構築して下さった方に感謝します（もちろん作者にも）。

Einsum.jlの紹介

Einsum.jlの概要

Pythonとの比較

実装詳細の話

オマケ

まとめ