Graph Laplacian Matrix の実装に関するメモ

Points

• Graph Laplacian matrix を実装し、具体的な数値例で確認。

Reference

1. A Tutorial on Spectral Clustering

Data

def create_data(n_input, dim, n_classes):

  n_input_per_class = n_input // n_classes

  x_1 = np.random.normal(loc = [7.0, 7.0], scale = [0.5, 0.5], size = [n_input_per_class, dim])
  x_2 = np.random.normal(loc = [5.0, 1.0], scale = [0.5, 0.5], size = [n_input_per_class, dim])
  x_3 = np.random.normal(loc = [2.0, 4.0], scale = [0.5, 0.5], size = [n_input_per_class, dim])

  x = np.concatenate([x_1, x_2, x_3], axis = 0).astype(np.float32)

  y_1 = np.array([0] * (n_input_per_class))
  y_2 = np.array([1] * (n_input_per_class))
  y_3 = np.array([2] * (n_input_per_class))

  y = np.concatenate([y_1, y_2, y_3]).astype(np.int32)
  y_one_hot = np.identity(n_classes)[y].astype(np.int32)
  
  return x, y, y_one_hot

  
n_input = 9
dim = 2
n_classes = 3

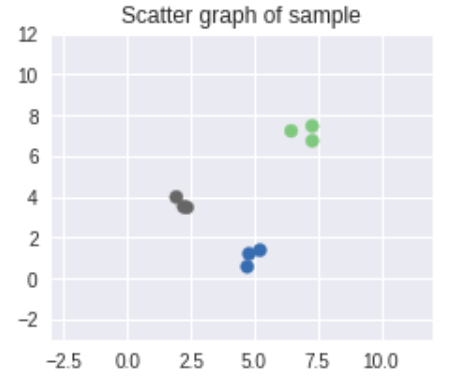
x, y, y_one_hot = create_data(n_input, dim, n_classes)

fig = plt.figure(figsize = (8, 3))

ax = fig.add_subplot(1, 2, 1)
ax.scatter(x[:, 0], x[:, 1], c = y, cmap = 'Accent')  # Accent
ax.set_xlim(-3.0, 12.0)
ax.set_ylim(-3.0, 12.0)
ax.set_title('Scatter graph of sample')

plt.show()

Sample Code

x_input = tf.expand_dims(x, 1)
M = tf.tile(x_input, [1, n_input, 1])
M_T = tf.transpose(M, [1, 0, 2])

# Gaussian similarity
sig = 1.0
W = tf.reduce_sum(tf.square(M - M_T), axis = -1)
W = tf.exp(-0.5 * W / sig**2)

# unnormalized Laplacian
diag = tf.reduce_sum(W, axis = -1)
D = tf.matrix_diag(diagonal = diag)
L = D - W 
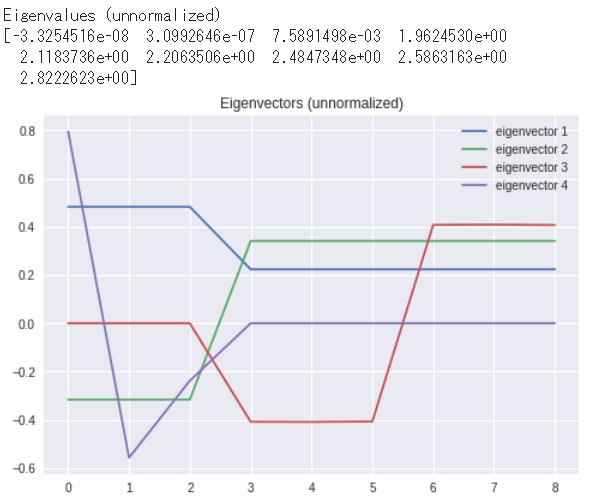
e, v = tf.self_adjoint_eig(L)

# normalized Laplacian
D_I = tf.matrix_diag(diagonal = 1.0 / diag)
L_rw = tf.matmul(D_I, L)
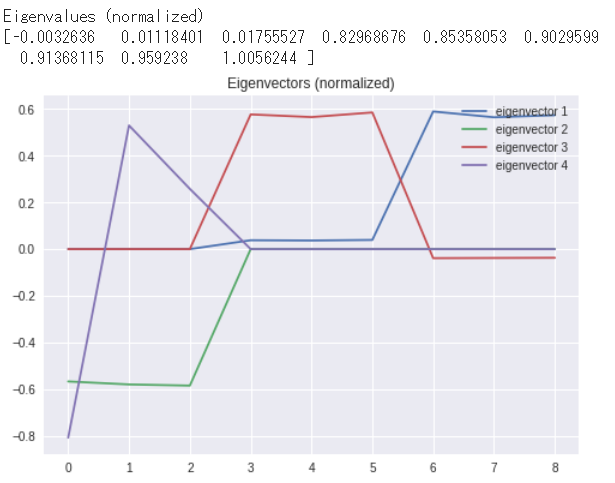
e_rw, v_rw = tf.self_adjoint_eig(L_rw)

with tf.Session() as sess:
  e = sess.run(e)
  v = sess.run(v)
  e_rw = sess.run(e_rw)
  v_rw = sess.run(v_rw)


print ('Eigenvalues (unnormalized)')  
print (e)
    
plt.plot(v[:, 0], label = 'eigenvector 1')
plt.plot(v[:, 1], label = 'eigenvector 2')
plt.plot(v[:, 2], label = 'eigenvector 3')
plt.plot(v[:, 3], label = 'eigenvector 4')
plt.title('Eigenvectors (unnormalized)')
plt.legend(loc = 'upper right')

plt.show()

print ('-' * 30)
print ('Eigenvalues (normalized)')  
print (e_rw)
    
plt.plot(v_rw[:, 0], label = 'eigenvector 1')
plt.plot(v_rw[:, 1], label = 'eigenvector 2')
plt.plot(v_rw[:, 2], label = 'eigenvector 3')
plt.plot(v_rw[:, 3], label = 'eigenvector 4')
plt.title('Eigenvectors (normalized)')
plt.legend(loc = 'upper right')