LSTM x Weight Normalization の実装に関するメモ

##ポイント

• LSTMをベースに Weight Normalization を実装。MNIST 手書き数字データでパフォーマンスを検証。
• Weight Normalization の効果を確認。
• Gradient Clipping の効果は今後、再検証。

##レファレンス
1. Weight Normalization: A Simple Reparameterization to Accelerate Training of Deep Neural Networks

##検証方法

• MNIST手書き数字データを使用。一層目の LSTM に Weight Normalization を適用。

• Base model（ Normalization なし）と比較。

• Weight Normalization

y = \phi(w \cdot x + b) \\
w = \frac{g}{||v||}v \\

　　　　　 　 　

##データ
MNIST handwritten digits

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('***/mnist', \
                                     one_hot = True)

##検証結果
数値計算例：

• n_units = 100
• learning_rate = 0.1
• batch_size = 64

Base

Weight Normalization ( no gradient clipping )

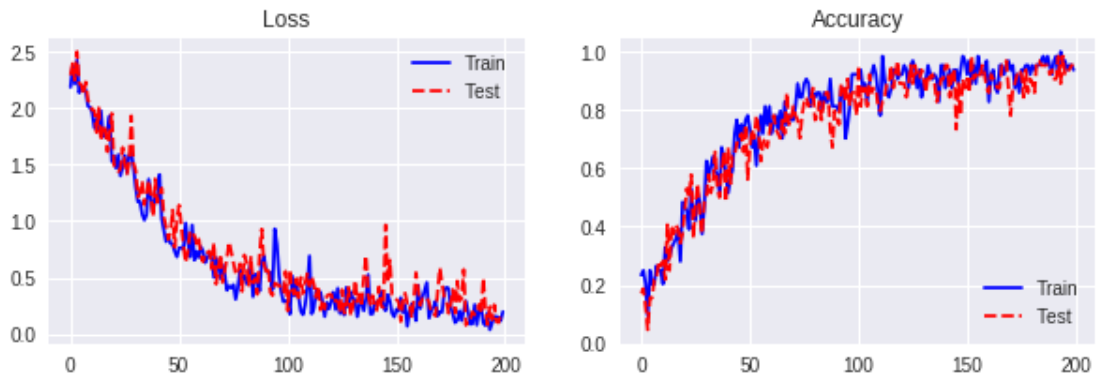
Weight Normalization ( clipped-by-norm, 0.5 )

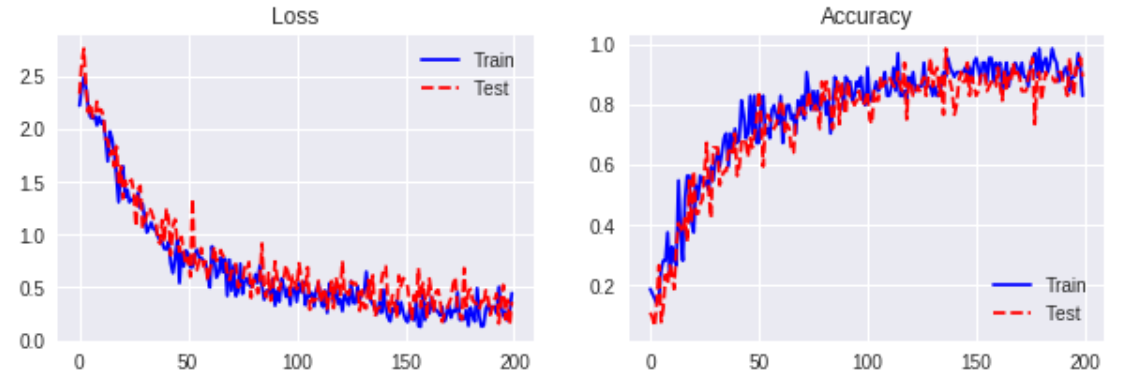
< br>

##サンプルコード

  # Weight Normalization
  def inference(self, x, length, n_in, n_units, n_out, \
                   batch_size, forget_bias):
    
    x = tf.reshape(x, [-1, length, n_in])

    h = tf.zeros(shape = [batch_size, n_units], \
                   dtype = tf.float32)
    c = tf.zeros(shape = [batch_size, n_units], \
                   dtype = tf.float32)
    
    list_h = []
    list_c = []
    
    with tf.variable_scope('lstm'):
      init_norm = tf.truncated_normal_initializer(mean = \
                   0.0, stddev = 0.05, dtype = tf.float32)
      init_constant1 = tf.constant_initializer(value = \
                   0.0, dtype = tf.float32)
      init_constant2 = tf.constant_initializer(value = \
                   0.1, dtype = tf.float32)
      
      v_x = tf.get_variable('w_x', shape = [n_in, n_units \
                   * 4], initializer = init_norm)
      g_x = tf.get_variable('g_x', shape = [n_units * 4], \
                   initializer = init_constant2)
      v_h = tf.get_variable('w_h', shape = [n_units, \
                   n_units * 4], initializer = init_norm)
      g_h = tf.get_variable('g_h', shape = [n_units * 4], \
                           initializer = init_constant2)
      b = tf.get_variable('b', shape = [n_units * 4], \
                   initializer = init_constant1)
      
      for t in range(length):
 
        v_norm_x = tf.nn.l2_normalize(v_x, axis = [0])
        w_x = g_x * v_norm_x
        t_x = tf.matmul(x[:, t, :], w_x)

        v_norm_h = tf.nn.l2_normalize(v_h, axis = [0])
        w_h = g_h * v_norm_h
        t_h = tf.matmul(h, w_h)
      
        i, f, o, g = tf.split(tf.add(tf.add(t_x, t_h), b), \
                         4, axis = 1)

        i = tf.nn.sigmoid(i)
        f = tf.nn.sigmoid(f + forget_bias)
        o = tf.nn.sigmoid(o)
        g = tf.nn.tanh(g)

        c = tf.add(tf.multiply(f, c), tf.multiply(i, g))
        h = tf.multiply(o, tf.nn.tanh(c))
        
        list_h.append(h)
        list_c.append(c)
        
    with tf.variable_scope('pred'):
      w = self.weight_variable('w', [n_units, n_out])
      b = self.bias_variable('b', [n_out])

      y = tf.add(tf.matmul(list_h[-1], w), b)
      y = tf.nn.softmax(y, axis = 1)
      
      return y

  def training(self, loss, learning_rate, clip_norm):
    optimizer = tf.train.AdamOptimizer(learning_rate = \
                   learning_rate)

    grads_and_vars = optimizer.compute_gradients(loss)
    clipped_grads_and_vars = [(tf.clip_by_norm(grad, \
           clip_norm = clip_norm), var) for grad, \
           var in grads_and_vars]
    train_step = \
        optimizer.apply_gradients(clipped_grads_and_vars)
    
    return train_step