0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

Day 19

身の回りの困りごとを楽しく解決！ by Works Human Intelligence Advent Calendar 2025

@takeru@github

1980年代のパズルを2025年のテクノロジーで力技で解く

Posted at

1980年代のパズルを2025年のテクノロジーで力技で解く

むかしむかし、だいたい今年の暑い夏の頃、実家にバラバラの青い棒のパズルが落ちていました。

3歳がバラバラにしたらしい。
このパズルおじさんが3歳の時からあったやつだぞ。

なおしたいなー。

これはなに？

いまは2025年、YouTubeで解き方動画あるやろ。。。
棒が6本、向きが8パターン、配置が、、、これは、、、、。

検索すると、Burr Puzzleというらしい。

image.png

https://burrtools.sourceforge.net/
https://www.puzzle-place.com/wiki/Solving_Burrs
https://www.robspuzzlepage.com/interlocking.htm
https://www.cs.brandeis.edu/~storer/JimPuzzles/BURR/000BURR/READING/IbmPage.pdf

数学的なお楽しみの歴史があるみたいでした。

データ構造

いや、でも、数学は無理ですので、力技で解きます。

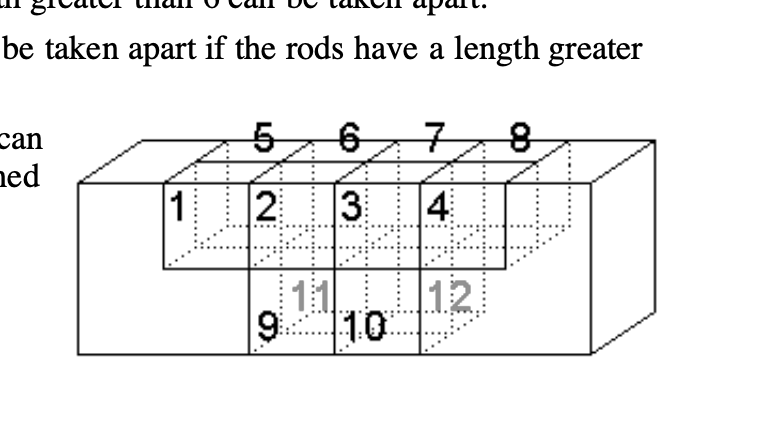
先輩たちのWeb情報によると、パズルの構造は以下のようになっています。

image.png

  • 棒が6本
  • 棒中央の欠けてる部分のルール
    • 上2x4
    • 下2x2(両端は欠けない)

よって、青いパズルのデータは以下のようになりました。

----
0001
0110
1001
1111
----
0011
0011
1111
1101
----
0000
0001
1111
1101
----
1110
1100
1111
1001
----
1000
0000
1001
1111
----
0001
0011
1101
1111
----

バー1本が占める範囲は2x2x4で、6本がうまくハマると4x4x4の範囲になります。

総当り、の前に

総当りで組み上がるパターンを見つけるだけ！

  • 初期位置での回転 4方向
  • 初期位置での向き 2パターン
  • 配置6箇所の組み合わせ 6 * 5 * 4 * 3 * 2

((4 * 2) ** 6) * (6 * 5 * 4 * 3 * 2) = 1.8億

どうだ？いけるのか？

data.py

marimoノートブックになっています。

marimo edit data.py

  • 初期位置での回転+向き → ローカル回転
  • 配置6箇所 → グローバル回転

になっていて、

  • パズル定義ファイルの読み込み
  • 回転と配置をした後のボクセル座標の計算

などがあります。

bits_to_voxels

バーの形状データ → ローカル回転 → グローバル回転 → 配置後の座標に変換する関数です。
回転は90度単位なので、sin/cosのテーブルをつくってnumpyで計算しています。
実際はこれを更にキャッシュを挟んで使っています。

def bits_to_voxels(
    bits: np.ndarray,
    local_rotation: Rotation,
    global_rotation: Rotation,
    position: Position,
):
    # bits: np.ndarray
    assert bits.shape == (4, 4)
    voxels = []
    for i, bbbb in enumerate(bits):
        y = -1 - (i // 2)
        z = i % 2 - 1
        for x, b in enumerate(bbbb):
            if b:
                voxels.append([x - 2, y, z])
    for x in [-3, 2]:
        for y in [-2, -1]:
            for z in [-1, 0]:
                voxels.append([x, y, z])

    # 90度単位の sin/cos 値の事前定義（整数値）
    # cos(0°)=1, cos(90°)=0, cos(180°)=-1, cos(270°)=0
    # sin(0°)=0, sin(90°)=1, sin(180°)=0, sin(270°)=-1
    cos_values = [1, 0, -1, 0]
    sin_values = [0, 1, 0, -1]

    # ローカル回転の中心点
    local_center = [-0.5, -1.5, -0.5]

    # 1. ローカル回転を適用
    # 回転角度を0-3の範囲に正規化
    lrx = local_rotation.x % 4
    lry = local_rotation.y % 4
    lrz = local_rotation.z % 4

    # ローカル回転行列を作成（事前定義された値を使用）
    # X軸回転
    LRx = np.array(
        [
            [1, 0, 0],
            [0, cos_values[lrx], -sin_values[lrx]],
            [0, sin_values[lrx], cos_values[lrx]],
        ]
    )

    # Y軸回転
    LRy = np.array(
        [
            [cos_values[lry], 0, sin_values[lry]],
            [0, 1, 0],
            [-sin_values[lry], 0, cos_values[lry]],
        ]
    )

    # Z軸回転
    LRz = np.array(
        [
            [cos_values[lrz], -sin_values[lrz], 0],
            [sin_values[lrz], cos_values[lrz], 0],
            [0, 0, 1],
        ]
    )

    # 合成ローカル回転行列
    LR = LRz @ LRy @ LRx

    # ローカル回転を適用
    local_rotated_voxels = []
    for v in voxels:
        # 中心点を原点に移動
        translated = np.array(
            [
                v[0] - local_center[0],
                v[1] - local_center[1],
                v[2] - local_center[2],
            ]
        )

        # ローカル回転を適用
        rotated = LR @ translated

        # 中心点を元に戻す
        final = [
            rotated[0] + local_center[0],
            rotated[1] + local_center[1],
            rotated[2] + local_center[2],
        ]
        local_rotated_voxels.append(final)

    # 2. グローバル回転を適用
    # グローバル回転の中心点
    global_center = [-0.5, -0.5, -0.5]

    # 回転角度を0-3の範囲に正規化
    grx = global_rotation.x % 4
    gry = global_rotation.y % 4
    grz = global_rotation.z % 4

    # グローバル回転行列を作成（事前定義された値を使用）

    # X軸回転
    GRx = np.array(
        [
            [1, 0, 0],
            [0, cos_values[grx], -sin_values[grx]],
            [0, sin_values[grx], cos_values[grx]],
        ]
    )

    # Y軸回転
    GRy = np.array(
        [
            [cos_values[gry], 0, sin_values[gry]],
            [0, 1, 0],
            [-sin_values[gry], 0, cos_values[gry]],
        ]
    )

    # Z軸回転
    GRz = np.array(
        [
            [cos_values[grz], -sin_values[grz], 0],
            [sin_values[grz], cos_values[grz], 0],
            [0, 0, 1],
        ]
    )

    # 合成グローバル回転行列
    # GR = GRz @ GRy @ GRx
    GR = GRx @ GRy @ GRz

    # グローバル回転を適用
    global_rotated_voxels = []
    for v in local_rotated_voxels:
        # 中心点を原点に移動
        translated = np.array(
            [
                v[0] - global_center[0],
                v[1] - global_center[1],
                v[2] - global_center[2],
            ]
        )

        # グローバル回転を適用
        rotated = GR @ translated

        # 中心点を元に戻して、最も近い整数座標に丸める
        final = np.round(
            [
                rotated[0] + global_center[0],
                rotated[1] + global_center[1],
                rotated[2] + global_center[2],
            ]
        ).astype(int)

        global_rotated_voxels.append(final.tolist())

    # 3. 位置を適用
    final_voxels = []
    for v in global_rotated_voxels:
        final_voxels.append(
            [v[0] + position.x, v[1] + position.y, v[2] + position.z]
        )

    return np.array(final_voxels)

あっているのか？

  • 書いたコードがあっているのか？
  • データ化したけど実際のパズルと一致してるのか？
  • プラスは右回り？左回り？XYZ軸？

見た目で確認できないと確信できませんので、Three.jsで可視化しました。
marimoノートブック内にThree.jsを埋め込んで表示できるようにしました。

marimo edit threejs.py

JSで書いたWidgetをmarimoノートブック内に埋め込める仕組みで、MarimoのUIで変数を変えると、リアクティブにJSの世界に反映させることができます。

with app.setup:
    # Initialization code that runs before all other cells
    import anywidget
    import traitlets

    CounterESM = """
    function render({ model, el }) {

      let button = document.createElement("button");

      button.addEventListener("click", () => {
        model.set("value", model.get("value") + 1);
        model.save_changes();
      });

      const updateInnerHTML = ()=>{
        button.innerHTML = `count=${model.get("value")} data=${model.get("data")}`;
      }
      updateInnerHTML();

      model.on("change:value", () => {
        updateInnerHTML();
      });

      model.on("change:data", () => {
        updateInnerHTML();
      });

      el.appendChild(button);
    }
    export default { render };
    """


@app.class_definition
class CounterWidget(anywidget.AnyWidget):
    _esm = CounterESM
    # Stateful property that can be accessed by JavaScript & Python
    value = traitlets.Int(0).tag(sync=True)
    data = traitlets.List([1, 2, 3]).tag(sync=True)


@app.cell
def _(mo):
    count_slider = mo.ui.slider(start=0, stop=100)
    return (count_slider,)


@app.cell
def _():
    counter_widget = CounterWidget()
    return (counter_widget,)


@app.cell
def _(count_slider, counter_widget):
    counter_widget.value = count_slider.value
    return

総当り

- 初期位置にバーを配置(4パターン)
- 2番目の位置にバーを配置(8パターン)
  - ぶつかってるなら次パターン、全パターン終わったら戻る
  - ぶつかってないなら
    - 3番目の位置にバーを配置(8パターン)
      - ぶつかってるなら次パターン、全パターン終わったら戻る
      - ぶつかってないなら
        - 4番目の位置にバーを配置(8パターン)
          - ぶつかってるなら次パターン、全パターン終わったら戻る
          - ぶつかってないなら
            - 5番目の位置にバーを配置(8パターン)
              - ぶつかってるなら次パターン、全パターン終わったら戻る
              - ぶつかってないなら
                - 6番目の位置にバーを配置(8パターン)
                  - ぶつかってるなら次パターン、全パターン終わったら戻る
                  - ぶつかってないなら
                    - 完成！

総当りとは言っても、ぶつかったパターンの先を計算するのは無駄なので省略します(バックトラック)。

@app.function
def solve(
    ctx, bars, placed_bar_and_patterns, bar_indices_to_placement, patterns
):
    # print(f"solve {placed_bar_and_patterns} {bar_indices_to_placement}")
    solutions = []
    bars_temp = []
    for placement, (bar_index, pattern) in enumerate(placed_bar_and_patterns):
        bar = bars[bar_index]
        bar.set_placement(placement)
        bar.set_pattern(pattern)
        bars_temp.append(bar)
    placed_voxcels = bars_to_voxels(bars_temp)

    for bar_index in bar_indices_to_placement:
        # print(f"bar_index={bar_index}")
        new_bar_indices_to_placement = [
            bi for bi in bar_indices_to_placement if bi != bar_index
        ]
        for pattern in patterns:
            new_bar = bars[bar_index]
            new_bar.set_placement(len(placed_bar_and_patterns))
            new_bar.set_pattern(pattern)
            new_bar_voxels = new_bar.voxels()
            has_collision = has_common_fast_numpy(
                placed_voxcels, new_bar_voxels
            )
            new_placed_bar_and_patterns = placed_bar_and_patterns + [
                (bar_index, pattern)
            ]
            if has_collision:
                pass
            else:
                if len(new_bar_indices_to_placement) == 0:
                    solution = new_placed_bar_and_patterns
                    ctx["callback"]({"solution": solution})
                    solutions.append(solution)
                else:
                    solutions += solve(
                        ctx,
                        bars,
                        new_placed_bar_and_patterns,
                        new_bar_indices_to_placement,
                        patterns,
                    )
    return solutions

完成！

これが2025年のおじさんが力技で解いた青いパズルの192パターンの解だ！

でも、どのバーも動かないんですけど！！デッドロック的な！

(つづく)

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?