LoginSignup
26
23

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@takeru0x5569(takeRu)

CORDICをFPGAに実装する

Posted at

CORDICアルゴリズム使用した論理回路を作成したので紹介をします。

今回の目標

三角関数（SINθ）を算出する回路をFPGAに実装します。

前提条件

  • アルゴリズムについての説明は割愛

    • FPGAに落とし込む際の具体的な方法について置き説明します

  • 固定小数を使用

    • 回路実装が容易な固定小数で実装します

  • 最後の除算はしない

    • CORDIC演算の最後の処理でX,Y座標を変換ベクトルで割る処理はしません（除算回路を入れたくないから）
    • 代替案としてX,Y座標の初期位置（1,1）のベクトル(√2)を、変換ベクトルで予め割った値を初期値とします。

  • 精度目標

    • 正弦波振動しているデバイスの基準信号(1周期に1トリガ)から、現在の角度を求めたい
    • 小数２桁くらいまで正確にもとめたい

  • パイプライン型の回路実装とする

    • 入力角度が毎サイクル更新される条件に対応したいため

  • 入力値（角度）

    • 固定少数で正数9bit,小数10bit
    • 正の数のみ
    • 360°以上の値を入力した場合は無効値として処理する（出力ENAをネゲートする）

  • 出力値

    • 16bitの２の補数表現とする

実装前準備

下準備として以下の２つを計算します。

  1. 角度参照テーブル
  2. XY座標初期値

角度参照テーブル

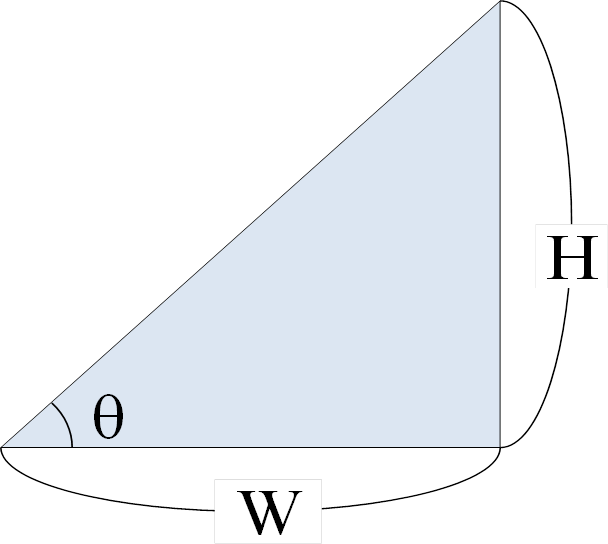
底辺がＷ、高さＨの直角三角形を用意し、角度をθとします。

TRI.png

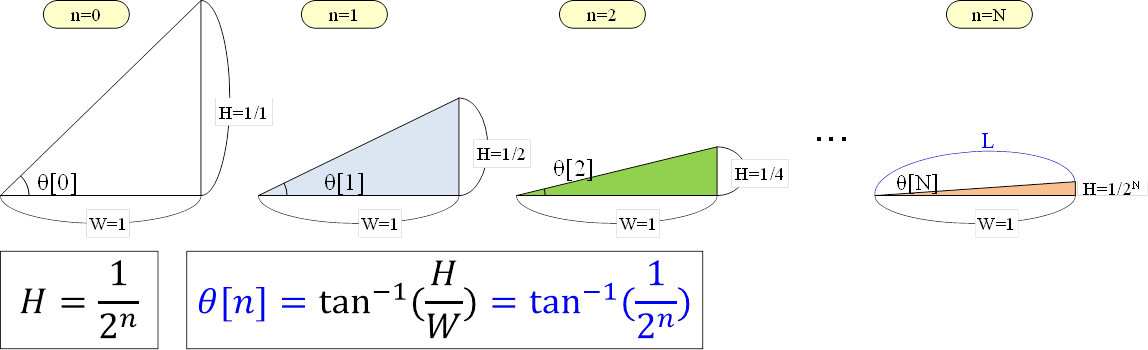
以下のとおり三角形をＮ回変形させて、角度θをテーブル化します。

  • 底辺Ｈは１に固定
  • 高さＨの 初期値を１ として、 Hを1/2^n倍ずつ 小さくする。
  • 角度θをアークタンジェントをnの関数として算出。（下図中の式参照）

TBL.png

XY座標初期値

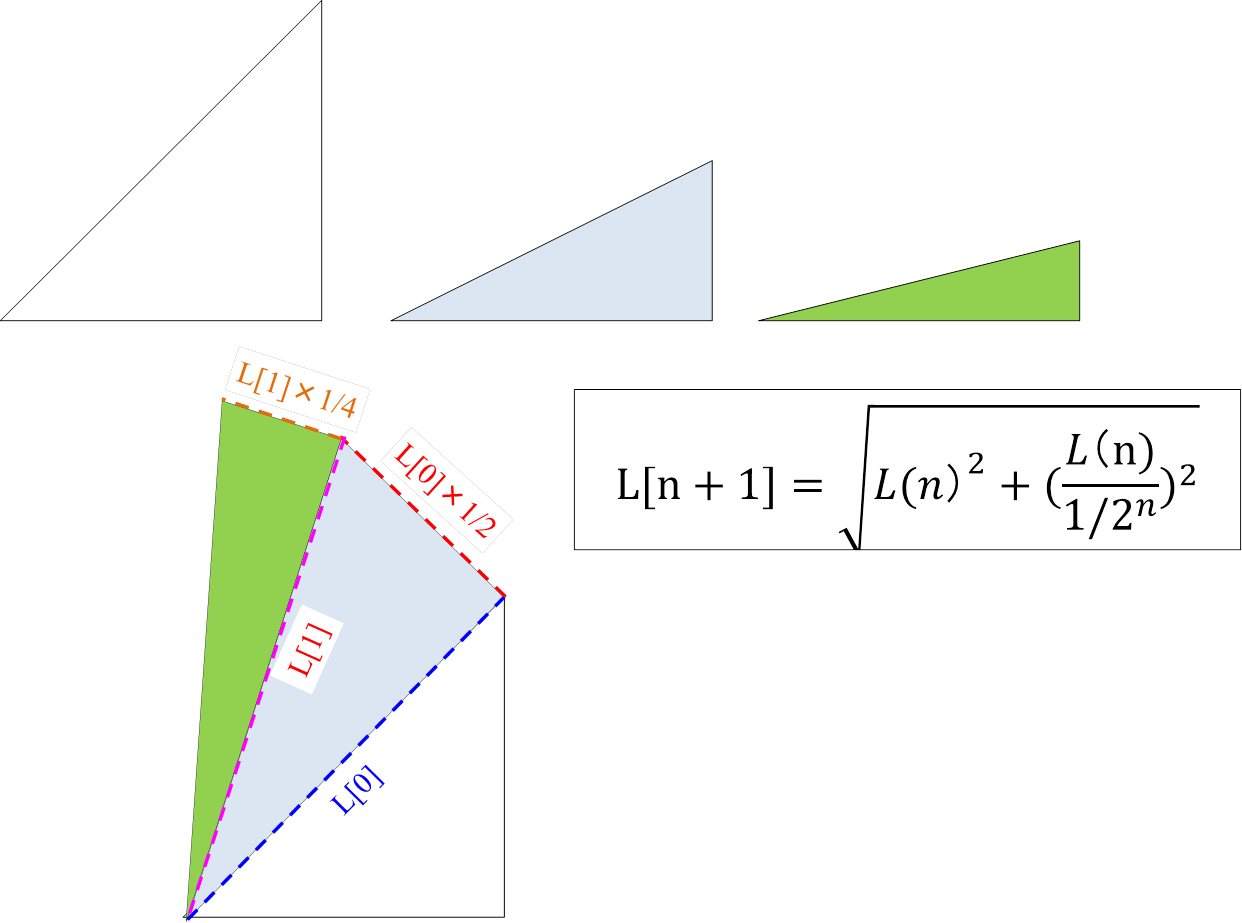
角度参照テーブルで求めた角度をもつ直角三角形を下図のように連結してゆきます。
このときn+1番目の三角の底辺Ｗがn番目の三角形の斜辺に一致するように、拡大しながら連結します。

このとき、以下の法則が成り立つので、拡大したｎ番目の三角形の斜辺Ｌ［ｎ］はピタゴラスの定理により算出できます。

  • ｎ番目の三角形の底辺Ｗ ＝ ｎ-1番目の斜辺
  • ｎ番目の三角形の高さＨ ＝ 底辺Ｗの　1/2＾n　

最終Ｎ番目の三角形の斜辺の長さ【Ｌ】が変換ベクトル【Ｒ】 です。
1/Ｒを予め求め、固定小数に変換した値を"ＸＹ座標の初期値"として適用することで除算回路を省略します。

CAL.png

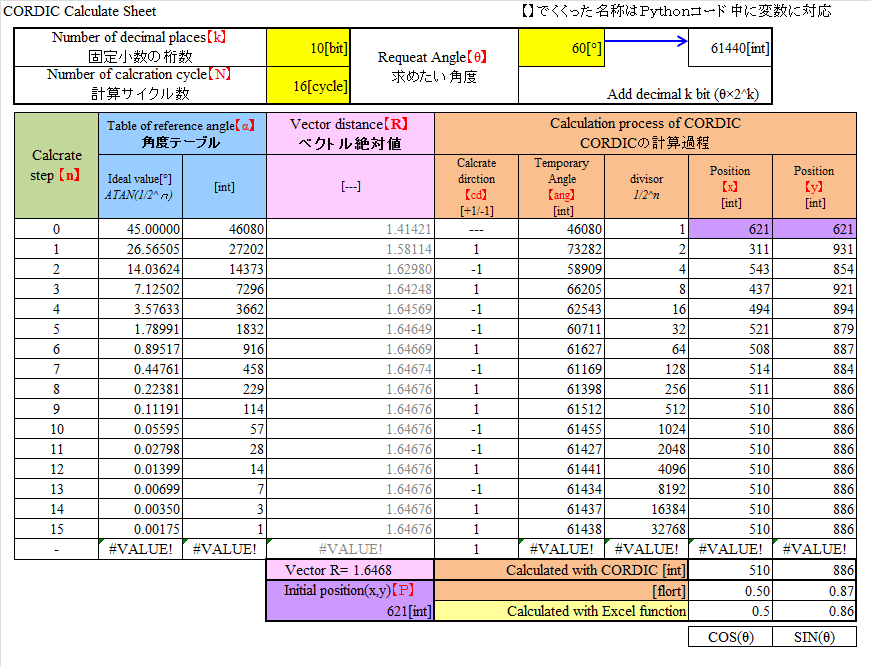
桁数と計算サイクル数

必要な桁数（小数bit幅）と計算サイクル数を予めＥｘｃｅｌで当たりをつけて以下のとおりとしました。

  • 小数桁数Ｋ＝10[bit]
  • 計算サイクル数Ｎ＝16[cycle]

誤差は出ていますが・・・

今回はパイプライン型の回路を組む為なるべくbit数/サイクル数は増やしたくないという理由で、この程度にとどめておきました。

CALC.png

事前検証

回路実装する前にPythonで事前検証した際のコードと結果を紹介します。

# -*- codinng:utf-8 -*-
import math
import sys

N=16   #計算サイクル数【Ｎ】
K=10    #固定小数点桁数【Ｋ】

# -----------------------------------------------
# 角度テーブル【α】を求める
# -----------------------------------------------
def table_gen():
    alph = []  #角度テーブル
    for i in range(N):
        # 1/2^n から高さが 1,1/2,1/4,1/8…となる角度(ラジアン)を算出
        rad = math.atan( 1/(2**i))
        #ラジアンから度に変換
        deg = math.degrees(rad)
        #固定小数分下駄をはかす
        ang_int =int(deg * (2**K))
        #角度テーブルに追加
        alph.append( ang_int )
    return alph

# -----------------------------------------------
# 座標の初期値
# -----------------------------------------------
def init_pos():
    #ベクトルＲの初期値は√２（45°の斜辺の長さ）
    r=math.sqrt(2)
    for i in range(1,N):
        #三角形の高さ（短い方の辺の長さ）＝1つ前の三角形の斜辺の長さの 1/(2^n)
        h = r / (2**i)
        #次の斜辺：ピタゴラスの定理で求める
        r = math.sqrt( (r**2) + (h**2) )
    #固定小数分下駄をはかせた１をＲで割って整数型にまるめる
    return int((2 ** K) / r)

# ------------------------------------------------------
# ＣＯＲＤＩＣ演算：SINθの演算
#   入力は0～360°以内とする
# ------------------------------------------------------
def cordic(theta , alph , init_position):
    #入力範囲逸脱チェック
    if theta>360 or theta<0 :
        print("inpur theta error!!")
        sys.exit()

    #求める角度:固定小数分下駄をはかせて端数捨て整数にする
    theta_int =int( theta * (2**K) )
    
    #360°を90°で4分割したエリアの該当位置判定　（pol：出力極性 　rvs：入力左右反転）
    grp = theta_int // (90 * 2**K)
    if grp ==0:     pol = 1 ;   rvs=False   #0～90°の場合
    elif grp ==1:   pol = 1 ;   rvs=True    #90～180°の場合
    elif grp ==2:   pol = -1 ;  rvs=False   #180～270°の場合
    elif grp ==3:   pol = -1 ;  rvs=True    #27～360°の場合

    #求めたい角度が0～90°の範囲になるようにする。
    nom_ang =  theta_int % (90 * 2**K)
    if rvs ==False:
        tgt_ang =  nom_ang
    else:
        tgt_ang =  90 * 2**K - nom_ang
    #x,ｙ座標の初期値
    x = init_position
    y = init_position
    #角度の初期値：45°に固定小数分下駄をはかせる
    ang = 45 * (2**K)

    for n in range(1,N):
        #演算方向決定
        if ang >= tgt_ang:
            cd = -1
        else:
            cd = 1
        #角度移動
        ang = ang + (cd * alph[n])
        #座標演算用シフト処理
        xd = x >> n
        yd = y >> n
        #座標移動先計算
        tmp_x = x - (cd * yd)
        tmp_y = y + (cd * xd)
        #座標移動
        x=tmp_x
        y=tmp_y
    #Y座標がそのままSIN（180°以上で負数）
    sin = pol * y
    #ＳＩＮθを返す
    return sin

# ---------------------------------------------------------------
# メイン関数
# ---------------------------------------------------------------
# 角度テーブルを生成
tbl =table_gen()
# 座標初期値
ip=init_pos()

# CORDICで0～360°を0.1°ステップで計算する
for i in range(3600):
    theta = i * 0.1
    sin= cordic(theta,tbl,ip)
    #SINθの結果（固定小数）をグラフプロット用の小数にする
    print (sin/2**K)

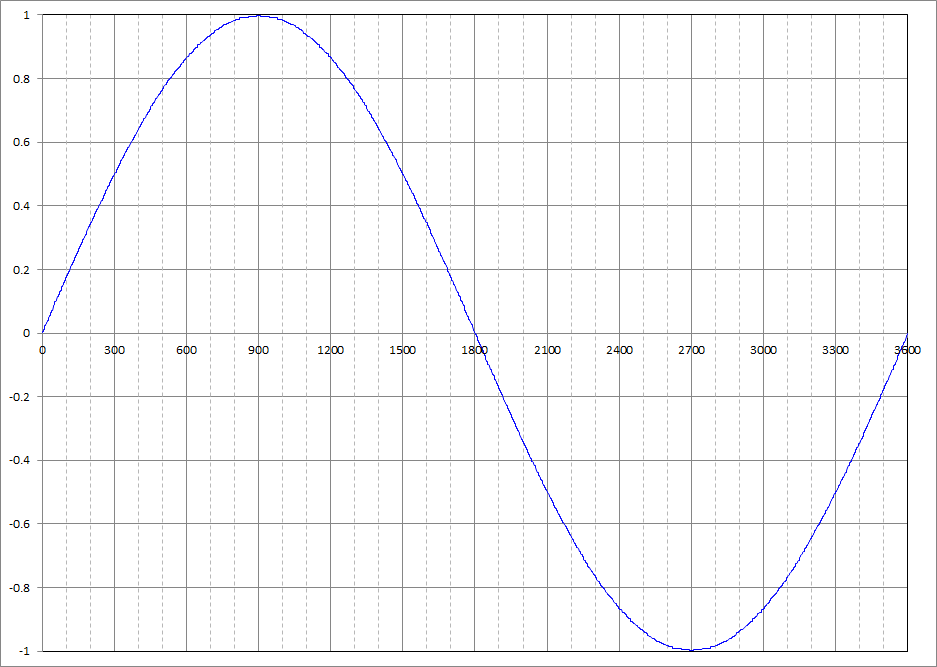
今回のbit精度から得られたSINカーブを下図に示します。（多少粗い印象ですが、要求には達していそうです）

SIN.png

RTL実装

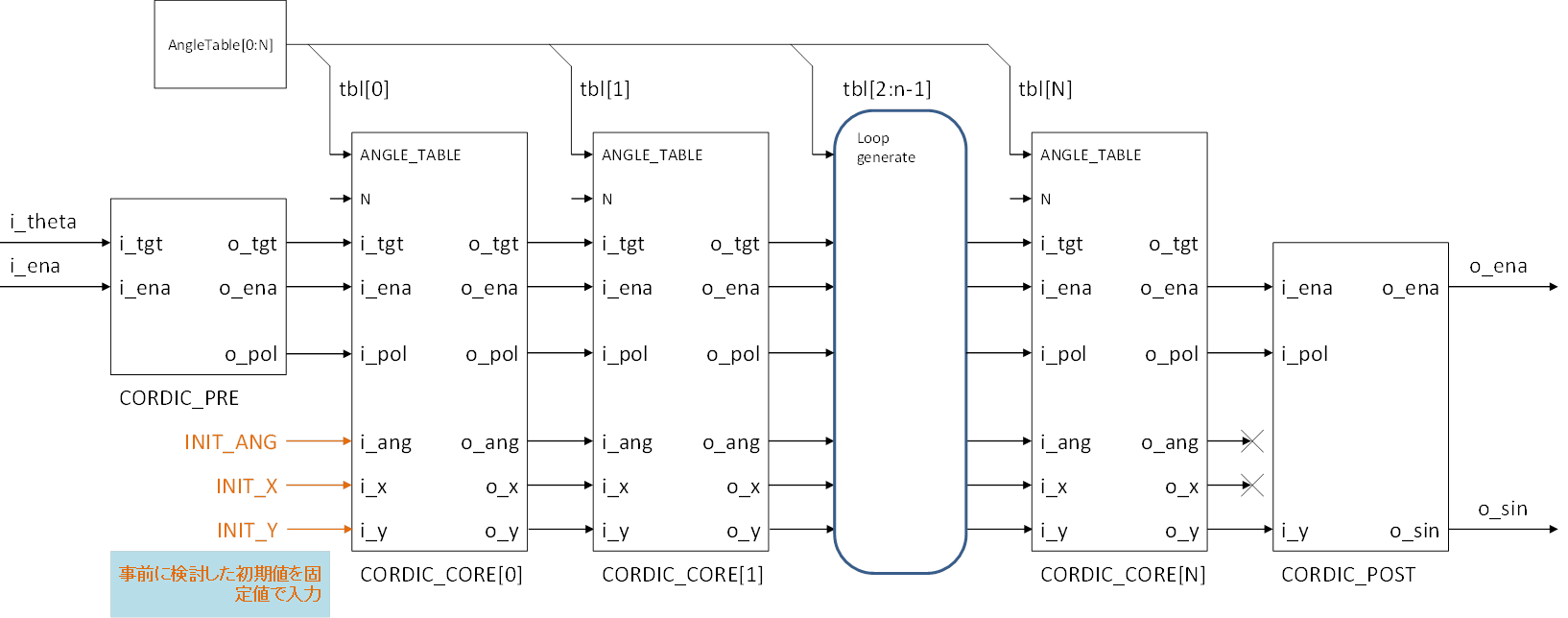
全体ブロック図

Pythonプログラムのforループ内の処理をCORDIC_COREモジュールに実装し、N段並べる構成にしました。

BLOCK.png

ブロック モジュール名 機能概要
角度テーブル AngleTable 予め計算しておいた角度デーブル（固定値）
前処理部 CORDIC_PRE 0～360°入力を0～90°に変換する。180°以上では出力極性を負数にするフラグ(o_pol)を立てる。
コア演算部 CORDIC_CORE XY座標演算のコアモジュール。Pythonコードのforループ１回転分の処理を行うモジュール。コアモジュールをシリアルN段接続してパイプラインを構成する。
後処理部 CORDIC_POST 極性フラグ(i_pol)に応じて符号反転するモジュール

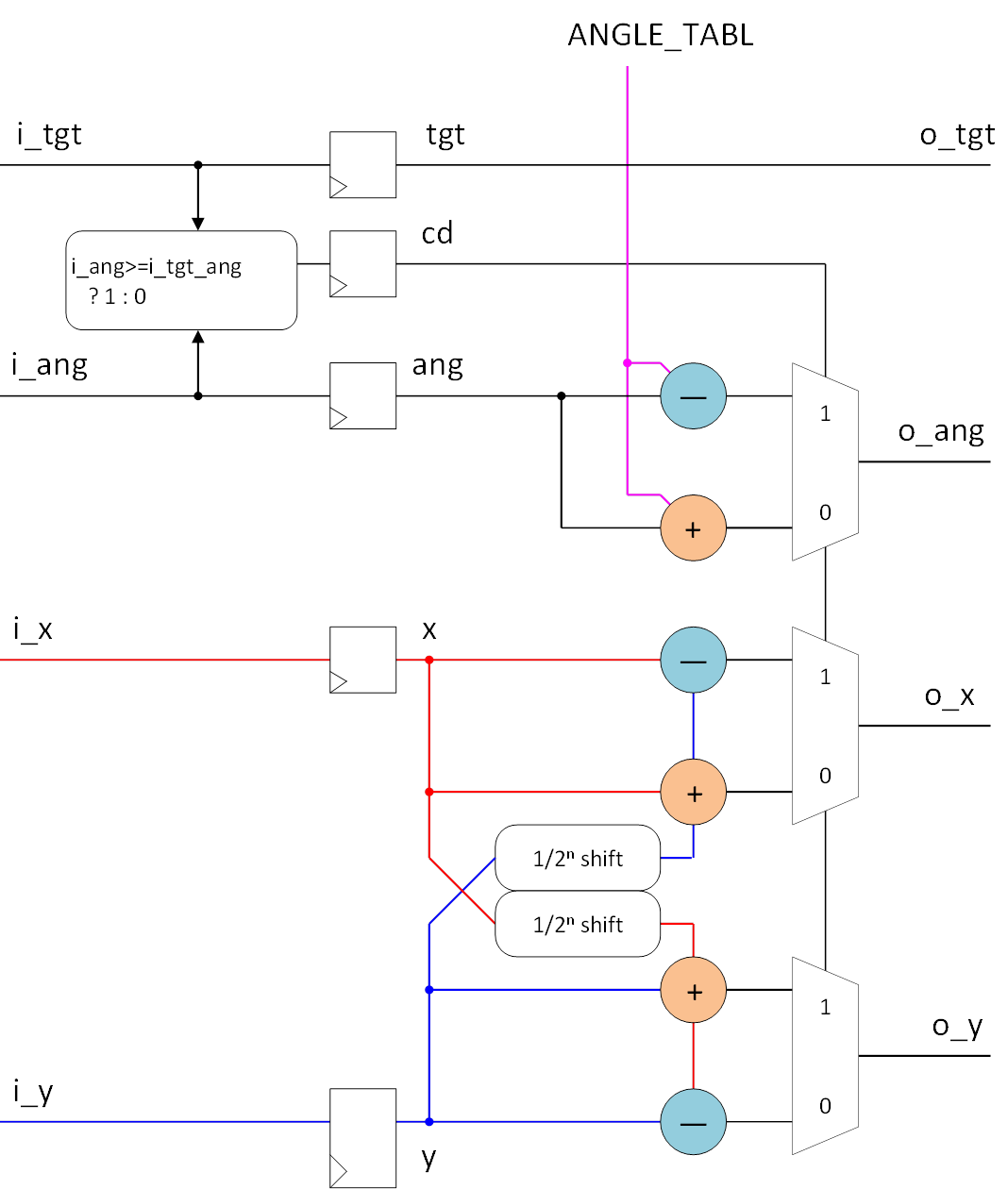
CORDICコアモジュール

RTL.png

  • 目標角度(i_tgt)と現在角度(i_ang)を比較し、cd( :Calcrate Dirctionの略)フラグを決定する
  • cdフラグに応じて加算or減算処理をセレクトする
  • 現在角度(i_ang)が負数（MSB=1)の場合は常に加算方向とする
  • シフト量nはパラメータ入力とする(ハード的には固定値)

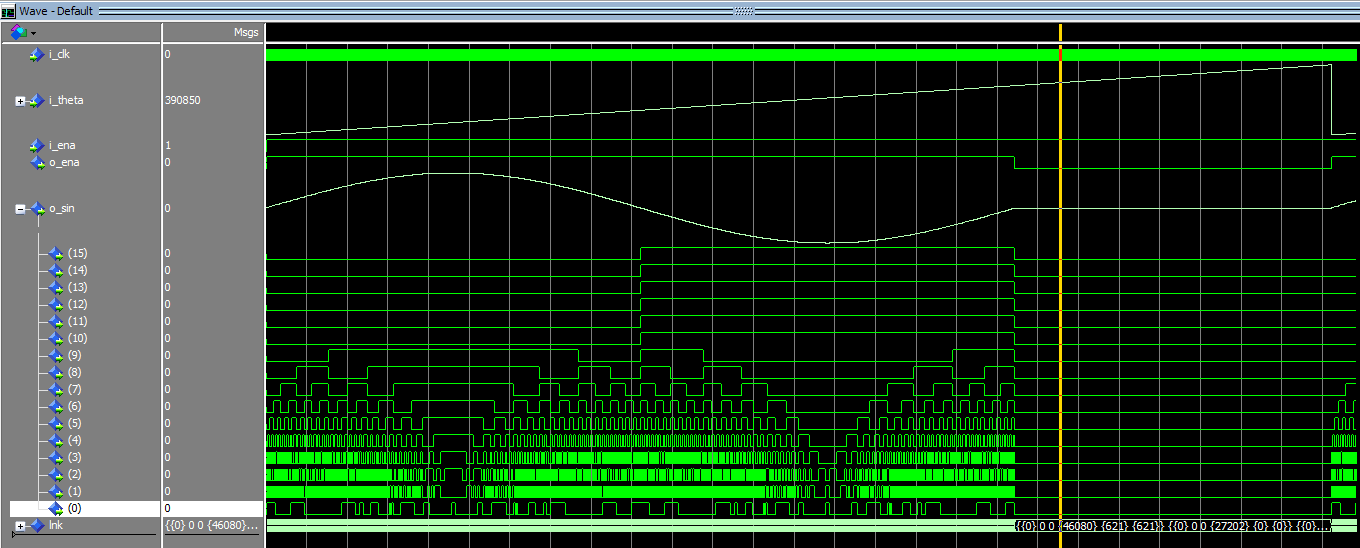
シミュレーション結果

入力角度(正数)を0から１LSBずつインクリメントしてゆくシミュレーションで、出力が正弦波（２の補数）となっていることを確認できました。

SIM.png

ソースコード

前処理部

	library ieee;
	use ieee.std_logic_1164.all;
	use ieee.std_logic_unsigned.all;
	use ieee.std_logic_arith.all;
	
	
	entity CORDIC_PRE is
		port(
		i_clk	:in		std_logic						;--クロック
		i_tgt	:in		std_logic_vector(18 downto 0)	;--目標角度0～360°(整数9bit 小数10bit)
		i_ena	:in		std_logic						;--イネーブル
		o_tgt	:out	std_logic_vector(16 downto 0)	;--目標角度0～90°(整数7bit 小数10bit)
		o_ena	:out	std_logic						;--イネーブル
		o_pol	:out	std_logic						);--出力極性フラグ()
	end entity;

architecture rtl of CORDIC_PRE is
	----------------------------------------------------------------
	--CONSTANT
	----------------------------------------------------------------
	--90,180,270度を固定少数10bitにした値
	constant	DEG90	:std_logic_vector(18 downto 0)	:=conv_std_logic_vector(90 ,9) & conv_std_logic_vector(0,10);
	constant	DEG180	:std_logic_vector(18 downto 0)	:=conv_std_logic_vector(180,9) & conv_std_logic_vector(0,10);
	constant	DEG270	:std_logic_vector(18 downto 0)	:=conv_std_logic_vector(270,9) & conv_std_logic_vector(0,10);
	constant	DEG360	:std_logic_vector(18 downto 0)	:=conv_std_logic_vector(360,9) & conv_std_logic_vector(0,10);
	
	constant	ANG90	:std_logic_vector(16 downto 0)	:=conv_std_logic_vector(90 ,7) & conv_std_logic_vector(0,10);
	----------------------------------------------------------------
	--SIGNAL
	----------------------------------------------------------------
	signal	d0_ena	:std_logic						:='0'			;
	signal	d0_tgt	:std_logic_vector(18 downto 0)	:=(others=>'0')	;
	
	signal	d1_ena	:std_logic						:='0'			;--
	signal	d1_pol	:std_logic						:='0'			;--出力極性反転フラグ(180°以上で負数に反転させる)
	signal	d1_rvs	:std_logic						:='0'			;--角度90°反転
	signal	nom_ang	:std_logic_vector(18 downto 0)	:=(others=>'0')	;--0～90°にノーマライズした角度
	
	signal	d2_ena	:std_logic						:='0'			;--
	signal	d2_pol	:std_logic						:='0'			;--
	signal	tgt_ang	:std_logic_vector(16 downto 0)	:=(others=>'0')	;--
	
begin
	
	--Stage0
	process(i_clk)begin
		if Rising_edge(i_clk) then
			--入力FF
			d0_ena	<=i_ena;
			d0_tgt	<=i_tgt;
		end if;
	end process;
	
	--Stage1
	process(i_clk)begin
		if Rising_edge(i_clk) then
			
			if(d0_tgt>=DEG360)then
				d1_ena	<='0';--360°以降は無効入力としてENAを落とす
			else
				d1_ena	<=d0_ena;
			end if;
			
			if(d0_tgt>=DEG360)then
				d1_pol	<='0';
				d1_rvs	<='0';
				nom_ang	<=(others=>'0');--360°以上が入力されたら0°として処理する
			elsif(d0_tgt>=DEG270)then
				d1_pol	<='1';
				d1_rvs	<='1';
				nom_ang	<=d0_tgt - DEG270;
			elsif(d0_tgt>=DEG180)then
				d1_pol	<='1';
				d1_rvs	<='0';
				nom_ang	<=d0_tgt - DEG180;
			elsif(d0_tgt>=DEG90)then
				d1_pol	<='0';
				d1_rvs	<='1';
				nom_ang	<=d0_tgt - DEG90;
			else
				d1_pol	<='0';
				d1_rvs	<='0';
				nom_ang	<=d0_tgt;
			end if;
		end if;
	end process;
	
	--Stage2
	process(i_clk)begin
		if Rising_edge(i_clk) then
			d2_ena	<=d1_ena;
			d2_pol	<=d1_pol;
			--90°反転フラグが立っていたら
			if(d1_rvs='0')then
				tgt_ang	<=nom_ang(16 downto 0);
			else
				tgt_ang	<=ANG90 - nom_ang(16 downto 0);
			end if;
			
		end if;
	end process;
	
	o_ena	<=d2_ena	;
	o_pol	<=d2_pol	;
	o_tgt	<=tgt_ang	;
end architecture;

コア演算部

	library ieee;
	use ieee.std_logic_1164.all;
	use ieee.std_logic_unsigned.all;
	
	entity CORDIC_CORE is
		generic(
		N				:integer 						;--シフト量
		ANGLE_TABLE		:std_logic_vector(16 downto 0)	);--角度参照テーブル
		port(
		i_clk	:in		std_logic						;--クロック
		i_tgt	:in		std_logic_vector(17 downto 0)	;--目標角度
		i_ena	:in		std_logic						;--イネーブル
		i_pol	:in		std_logic						;--出力極性反転フラグ
		i_ang	:in		std_logic_vector(17 downto 0)	;--現在角度
		i_x		:in		std_logic_vector(15 downto 0)	;--座標X
		i_y		:in		std_logic_vector(15 downto 0)	;--座標Y
		o_tgt	:out	std_logic_vector(17 downto 0)	;--
		o_ena	:out	std_logic						;--
		o_pol	:out	std_logic						;--
		o_ang	:out	std_logic_vector(17 downto 0)	;--
		o_x		:out	std_logic_vector(15 downto 0)	;--
		o_y		:out	std_logic_vector(15 downto 0)	);--
	end entity;

architecture rtl of CORDIC_CORE is
	signal	tgt		:std_logic_vector(17 downto 0)	:=(others=>'0')	;
	signal	ena		:std_logic						:='0'			;
	signal	pol		:std_logic						:='0'			;
	signal	cd		:std_logic						:='0'			;
	signal	ang		:std_logic_vector(17 downto 0)	:=(others=>'0')	;
	signal	x		:std_logic_vector(15 downto 0)	:=(others=>'0')	;
	signal	y		:std_logic_vector(15 downto 0)	:=(others=>'0')	;
	
	signal	ang_tbl	:std_logic_vector(17 downto 0)	;
	signal	sft_x	:std_logic_vector(15 downto 0)	;
	signal	sft_y	:std_logic_vector(15 downto 0)	;
	
begin
	
	--入力FF
	process(i_clk)begin
		if Rising_edge(i_clk) then
			if(i_ena='1')then
				tgt	<=i_tgt;
				ena	<='1';
				
				if(i_ang(i_ang'high)='1')then --MSBが１は負数なので常に足す
					cd	<='0';--角度足す方向
				else
					if(i_ang>=i_tgt)then
						cd	<='1';--角度引く方向
					else
						cd	<='0';--角度足す方向
					end if;
				end if;
				x	<=i_x;
				y	<=i_y;
				ang	<=i_ang;
				pol	<=i_pol;
			else
				tgt	<=(others=>'0');
				ena	<='0';
				cd	<='0';
				x	<=(others=>'0');
				y	<=(others=>'0');
				ang	<=(others=>'0');
				pol	<='0';
			end if;
		end if;
	end process;
	
	--シフト
	GEN:for i in 0 to 15 generate
		GENIF:if i >=(15-N)generate
			sft_x(i)	<=x(15);
			sft_y(i)	<=y(15);
		end generate;
		
		GENIF2:if i <(15-N)generate
			sft_x(i)	<=x(i+N+1);
			sft_y(i)	<=y(i+N+1);
		end generate;
	end generate;
	
	--符号bit付加
	ang_tbl	<='0' & ANGLE_TABLE;
	
	--目標角度
	o_tgt	<=tgt;
	
	--イネーブル
	o_ena	<=ena;
	o_pol	<=pol;
	
	--現在角度
	o_ang	<=	ang - ang_tbl when(cd='1')else
				ang + ang_tbl;
	
	--X座標
	o_x		<=	x - sft_y	when(cd='0')else
				x + sft_y;
	
	--Y座標
	o_y		<=	y + sft_x	when(cd='0')else
				y - sft_x;
	
end architecture;

後処理部

	library ieee;
	use ieee.std_logic_1164.all;
	use ieee.std_logic_unsigned.all;
	use ieee.std_logic_arith.all;
	
	
	entity CORDIC_POST is
		port(
		i_clk	:in		std_logic						;--クロック
		i_tgt	:in		std_logic_vector(17 downto 0)	;--目標角度
		i_ena	:in		std_logic						;--イネーブル
		i_pol	:in		std_logic						;--出力極性反転フラグ
		i_y		:in		std_logic_vector(15 downto 0)	;--座標Y
		o_ena	:out	std_logic						;--
		o_sin	:out	std_logic_vector(15 downto 0)	);--
	end entity;

architecture rtl of CORDIC_POST is
	----------------------------------------------------------------
	--SIGNAL
	----------------------------------------------------------------
	signal	ena	:std_logic						:='0'			;
	signal	pol	:std_logic						:='0'			;
	signal	y	:std_logic_vector(15 downto 0)	:=(others=>'0')	;
	
	signal	ena1:std_logic						:='0'			;
	signal	sin	:std_logic_vector(15 downto 0)	:=(others=>'0')	;
	
begin
	
	--Stage0
	process(i_clk)begin
		if Rising_edge(i_clk) then
			if(i_ena='1')then
				ena	<='1'	;
				pol	<=i_pol	;
				y	<=i_y	;
			else
				ena	<='0'			;
				pol	<='0'			;
				y	<=(others=>'0')	;
			end if;
		end if;
	end process;
	
	--Stage1
	process(i_clk)begin
		if Rising_edge(i_clk) then
			ena1<=ena;
			
			if(pol='0')then
				sin	<=y		;
			else
				sin	<=(not y) + 1;
			end if;
		end if;
	end process;
	
	o_ena	<=ena1;
	o_sin	<=sin;
	
end architecture;

トップ

	library ieee;
	use ieee.std_logic_1164.all;
	use ieee.std_logic_arith.all;
	use ieee.std_logic_unsigned.all;
	
entity CORDIC is
	port(
		i_clk	:in		std_logic						;--クロック
		i_theta	:in		std_logic_vector(18 downto 0)	;--目標角度0～360°(整数9bit 小数10bit)
		i_ena	:in		std_logic						;--イネーブル
		o_ena	:out	std_logic						;--イネーブル
		o_sin	:out	std_logic_vector(15 downto 0)	);--
end entity;

architecture rtl of CORDIC is
	----------------------------------------------------
	--User type
	----------------------------------------------------
	--コア間接続信号をまとめたタイプ
	type typ_LINK_CORE is record
		tgt	:std_logic_vector(17 downto 0)	;--
		ena	:std_logic						;--
		pol	:std_logic						;--
		ang	:std_logic_vector(17 downto 0)	;--
		x	:std_logic_vector(15 downto 0)	;--
		y	:std_logic_vector(15 downto 0)	;--
	end record;
	
	--コア間接続信号タイプのアレイ
	type typ_LINK_CORE_ARY is
		array(integer range<>) of typ_LINK_CORE;
	
	type typ_ANGLE_TABLE is
		array(integer range<>) of std_logic_vector(16 downto 0);
	----------------------------------------------------
	--Signal
	----------------------------------------------------
	signal	lnk	:typ_LINK_CORE_ARY(0 to 15)	;
	
	
	constant	N			:integer :=15;--パイプライン段数
	constant	INIT_ANG	:std_logic_vector(17 downto 0):=conv_std_logic_vector(46080,18);
	constant	INIT_X		:std_logic_vector(15 downto 0):='0'&conv_std_logic_vector(621,15);
	constant	INIT_Y		:std_logic_vector(15 downto 0):='0'&conv_std_logic_vector(621,15);
	
	constant	ANGLE_TABLE	:typ_ANGLE_TABLE(0 to N)
		:=	("0"&x"B400"
			,"0"&x"6A42"
			,"0"&x"3825"
			,"0"&x"1C80"
			,"0"&x"0E4E"
			,"0"&x"0728"
			,"0"&x"0394"
			,"0"&x"01CA"
			,"0"&x"00E5"
			,"0"&x"0072"
			,"0"&x"0039"
			,"0"&x"001C"
			,"0"&x"000E"
			,"0"&x"0007"
			,"0"&x"0003"
			,"0"&x"0001"
			);

begin
	--前処理部：角度0～90°正規化
	u_CORDIC_PRE:entity work.CORDIC_PRE
		port map
		(i_clk	=>i_clk
		,i_tgt	=>i_theta
		,i_ena	=>i_ena
		,o_tgt	=>lnk(0).tgt(16 downto 0)
		,o_ena	=>lnk(0).ena
		,o_pol	=>lnk(0).pol
		);
		
	--初期値 
	lnk(0).tgt(17)	<='0'		;
	lnk(0).ang		<='0'&ANGLE_TABLE(0);--INIT_ANG	;
	lnk(0).x		<=INIT_X	;
	lnk(0).y		<=INIT_Y	;
	
	--コアモジュールシリアル接続
	GEN_CORDIC: for i in 0 to N-1 generate
		u_CORDIC_CORE:entity work.CORDIC_CORE
			generic map
			(N				=>i
			,ANGLE_TABLE	=>ANGLE_TABLE(i+1)
			)
			port map
			(i_clk	=>i_clk			
			,i_tgt	=>lnk( i ).tgt	
			,i_ena	=>lnk( i ).ena	
			,i_pol	=>lnk( i ).pol	
			,i_ang	=>lnk( i ).ang	
			,i_x	=>lnk( i ).x	
			,i_y	=>lnk( i ).y	
			,o_tgt	=>lnk(i+1).tgt	
			,o_ena	=>lnk(i+1).ena	
			,o_pol	=>lnk(i+1).pol	
			,o_ang	=>lnk(i+1).ang	
			,o_x	=>lnk(i+1).x	
			,o_y	=>lnk(i+1).y	
			);
	end generate;
	
	
	CORDIC_POST:entity work.CORDIC_POST
		port map
		(i_clk	=>i_clk
		,i_tgt	=>lnk(N).tgt	
		,i_ena	=>lnk(N).ena	
		,i_pol	=>lnk(N).pol	
		,i_y	=>lnk(N).y	
		,o_ena	=>o_ena
		,o_sin	=>o_sin
		);
	
end architecture;

注意点

  • 実機検証までは至っていないので、回路規模や速度まで含めた最適化までは完了していません。
26
23
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
26
23

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?