競馬予想
Deep learning が流行っているので何かを題材に勉強してみようと思い、競馬予想をしてみたメモです。
投資競馬 Advent Calendar 2016 7日目の記事です。
環境構築
Install pyenv, python(annaconda)
↓を参考に Python 3.5.1 :: Anaconda 4.0.0 をインストール
Install Chainer
Chainer をインストールします。
pip install chainer
データ収集
JRA-VAN というJRAの子会社が運営しているサービスがあります。有料ですが1ヶ月無料トライアルもあります。
今回は無料トライアルでデータを集めます。
JRA-VAN のデータを取り込むソフトは複数あるみたいですがTARGET frontier JVというものがデータを csv 出力できるようなのでこちらを使います。
ちなみにJRA-VAN対応のソフトが Windows 用のソフトしかないのでこの作業は Windows で行います。
#データ仕様は公開されているらしいのですが自分で読み込むのは大変そうなのでパスします。
データ取り込み
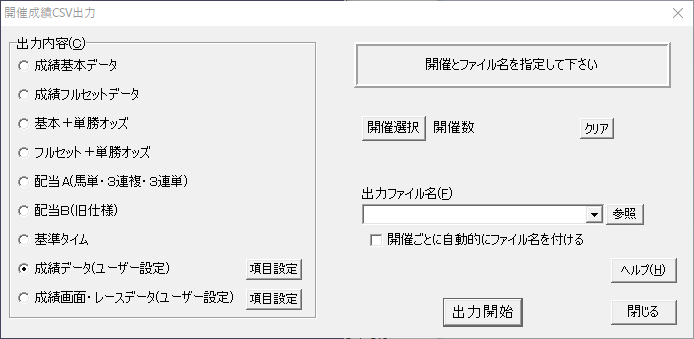
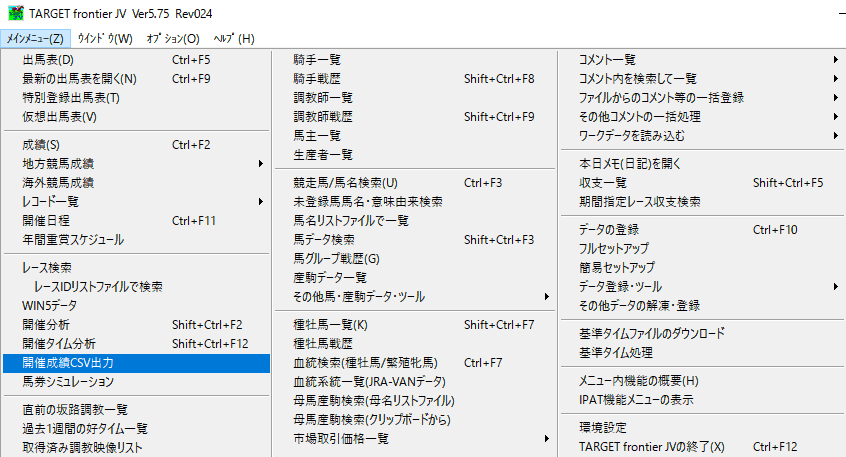
・TARGET frontier JV を起動して「メニュー」→「開催成績CSV」を選択
・「成績データ(ユーザー設定)」を選択
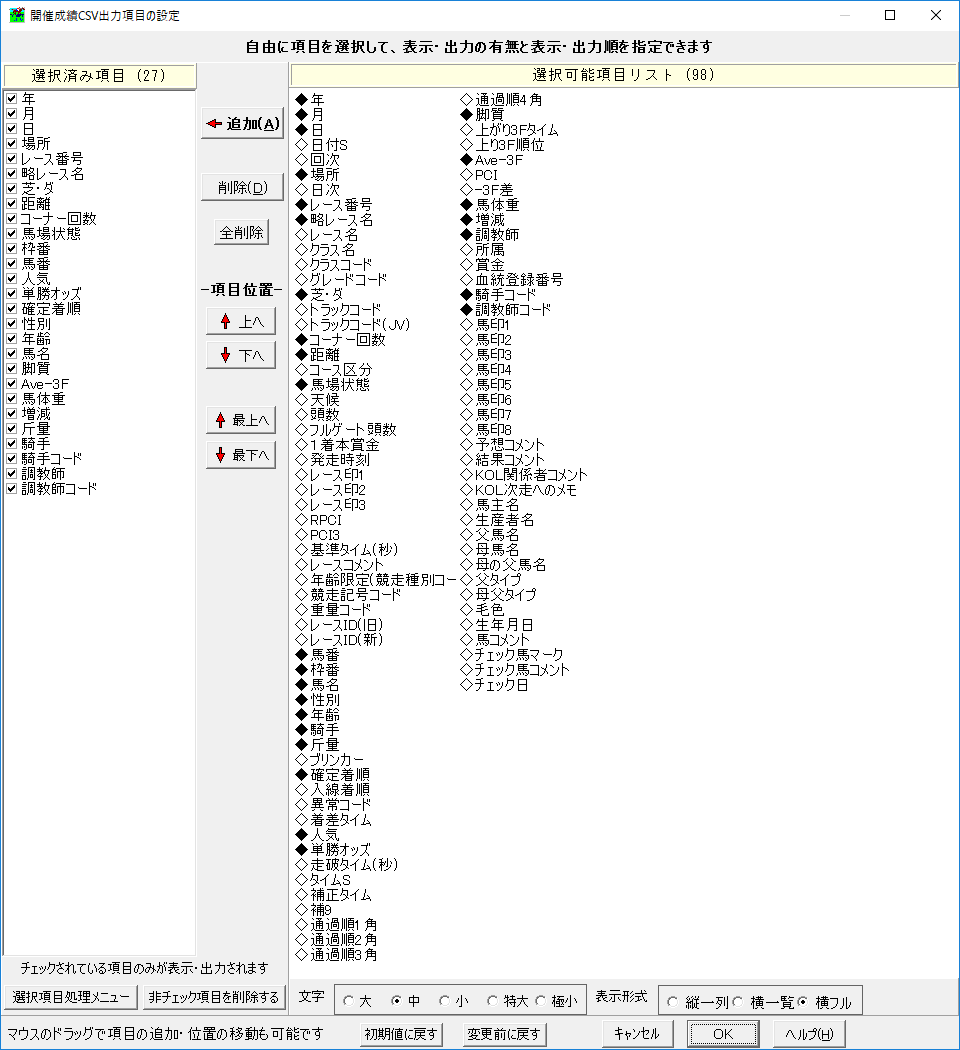
・学習に必要な項目を選択します。ここがポイントだと思いますがよくわからないのでなんとなくで決めます(下の画像参照)。
項目を決めたら出力する年数・競馬場を選択して出力します。
そうすると下記のようなデータが得られました。
07,08,11,札幌,1,未勝利*,芝,1500,3,稍,1,1,5,16.2,3,牡,2,テーオーブラック,先行,35.87,442,-14,53.0,北村友一,01102,梅田智之,01084
07,08,11,札幌,1,未勝利*,芝,1500,3,稍,2,2,6,22.8,12,牡,2,メイショウアーリー,中団,36.07,464,+4,54.0,秋山真一,01019,安田伊佐,00340
07,08,11,札幌,1,未勝利*,芝,1500,3,稍,3,3,11,162.0,11,牡,2,サンデーチャリティ,後方,36.53,424,+6,51.0,黛弘人,01109,高松邦男,00219
...
Chainer で予想
Chainer での学習については mnist のサンプルを参考に入力データを用意します。
- 入力データ:float32 の2次元配列。ここでは配列に1レース分の情報を含め、その配列を入力とします。
- 正解(ラベル)データ:int32 の配列。mnist では正解の数字が入っていましたがここでは各レースの1着の馬番を入れます。
データ読み込み
Chainer で学習させるには csv ファイルから numpy array にデータを読み込みます。一部の日程のレース結果を検証データ、その他を学習データとして読み込みます。
Chainer への入力データは float32 で統一するので csv ファイルに含まれる文字列データは数値に変換します。変換には下記のような dictionary を用意します。
self.dataMap = {
3 : { "札幌": 0, "函館": 1, "福島": 2, "東京": 3, "中山": 4, "京都": 5, "新潟": 6, "阪神": 7, "中京": 8, "小倉": 9 },
6 : { "芝" : 0, "ダ" : 1 },
9 : { "不" : 0, "重" : 1, "稍" : 2, "良" : 3 },
15 : {"牡" : 0, "牝" : 1, "セ" : 2},
18 : {"逃げ" : 0, "先行" : 1, "中団" : 2, "差し" : 3, "後方" : 4, "追込" : 5, "マクリ" : 6, "" : 7}
}
pickle
csv の読み込みもデータ量が大きくなると時間がかかるので一度読み込んだら dump しておき、学習時にはこちらを使います。
python には pickle というオブジェクトをファイルに書き出せるライブラリがあるのでそれを使います。
import pickle as P
# 書き出し
with open('train_data.pickle', 'wb') as f:
P.dump(self.train_data, f)
# 読み出し
with open('train_data.pickle', 'rb') as f:
self.train_data = P.load(f)
学習&検証
競馬予想にどのモデルが適しているのか分からないので mnist のサンプルのままで試してみました。
mnist と異なり競馬は最大18頭でレースをするので output だけ 18 に変更します。
class MLP(chainer.Chain):
def __init__(self, n_units, n_out):
super(MLP, self).__init__(
# the size of the inputs to each layer will be inferred
l1=L.Linear(None, n_units), # n_in -> n_units
l2=L.Linear(None, n_units), # n_units -> n_units
l3=L.Linear(None, n_out), # n_units -> n_out
)
def __call__(self, x):
h1 = F.relu(self.l1(x))
h2 = F.relu(self.l2(h1))
return self.l3(h2)
model = L.Classifier(MLP(args.unit, 18))
実行結果
mnist のモデルのままだと精度がほとんど上がりませんでした。データの見直しやモデルの検討がまだまだ必要そうですね。
# unit: 1000
# Minibatch-size: 100
# epoch: 40
train_data count = 33972
train_data_answer count = 33972
test_data count = 263
test_data_answer count = 263
epoch main/loss validation/main/loss main/accuracy validation/main/accuracy elapsed_time
1 53.3197 2.88323 0.072 0.086455 6.08774
2 2.8392 2.86606 0.0755 0.0778307 11.7691
3 2.80957 2.84367 0.0756471 0.081164 25.6663
4 2.79768 2.93953 0.0758407 0.081164 39.172
5 2.79359 2.81899 0.0761471 0.0831217 52.5182
6 2.78751 2.82241 0.0754118 0.0644974 65.9139
7 2.78489 2.8214 0.0740882 0.0644974 79.0856
8 2.78344 2.8256 0.0753392 0.0644974 92.4037
9 2.78374 2.80649 0.0748824 0.0644974 105.891
10 2.78153 2.81414 0.0760588 0.0644974 119.413
11 2.78305 2.80919 0.0756047 0.061164 133.375
12 2.78163 2.81012 0.0749706 0.0644974 147.492
13 2.78179 2.81818 0.0759706 0.061164 160.974
14 2.78133 2.81274 0.0743529 0.0678307 174.484
15 2.78157 2.81185 0.0747493 0.0678307 188.008
16 2.78114 2.81094 0.0746765 0.0678307 201.59
17 2.78222 2.8136 0.0759706 0.0678307 215.782
18 2.78156 2.81085 0.0758407 0.0644974 229.198
19 2.78261 2.81022 0.0743529 0.0678307 242.806
20 2.78189 2.81007 0.0737353 0.0678307 256.197
21 2.78089 2.8106 0.0752647 0.0678307 269.714
22 2.78256 2.81243 0.0749853 0.0678307 283.141
23 2.78154 2.81041 0.0757059 0.0678307 296.677
24 2.78148 2.81015 0.0744706 0.0678307 310.393
25 2.78165 2.81023 0.0750442 0.0678307 324.221
26 2.78157 2.81032 0.0757353 0.0678307 338.199
27 2.7815 2.81081 0.0756176 0.0678307 352.488
28 2.78158 2.81084 0.0752353 0.0831217 366.459
29 2.78158 2.81058 0.0738348 0.0831217 380.612
30 2.78151 2.81075 0.0745882 0.0678307 395.066
31 2.78159 2.81096 0.0750882 0.0678307 409.354
32 2.7814 2.8106 0.0756176 0.0678307 423.486
33 2.78167 2.81094 0.0741593 0.0678307 437.62
mnist に2層追加
試しに mnist のネットワークに2層追加してみました。
class MLP(chainer.Chain):
def __init__(self, n_units, n_out):
super(MLP, self).__init__(
# the size of the inputs to each layer will be inferred
l1=L.Linear(None, n_units), # n_in -> n_units\
l2=L.Linear(None, n_units), # n_units -> n_units
l3=L.Linear(None, n_units), # n_units -> n_units
l4=L.Linear(None, n_units), # n_units -> n_units
l5=L.Linear(None, n_out), # n_units -> n_out
)
def __call__(self, x):
h1 = F.relu(self.l1(x))
h2 = F.relu(self.l2(h1))
h3 = F.relu(self.l3(h2))
h4 = F.relu(self.l4(h3))
return self.l5(h4)
結果は mnist オリジナルよりも良くなったように見えますが安定してない&学習データの精度だけ上がってるので過学習になってそうでもあります。
# unit: 600
# Minibatch-size: 100
# epoch: 40
train_data count = 33972
train_data_answer count = 33972
test_data count = 263
test_data_answer count = 263
loader.train_data = float32, shape = (33972, 240)
loader.train_data_answer = int32, shape = (33972,)
loader.test_data = float32, shape = (263, 240)
loader.test_data_answer = int32, shape = (263,)
epoch main/loss validation/main/loss main/accuracy validation/main/accuracy elapsed_time
1 12.466 2.91101 0.0711765 0.0731217 5.70191
2 2.7585 2.84412 0.0864118 0.0903704 11.2326
3 2.70088 2.81017 0.0917059 0.0997884 23.8984
4 2.67644 2.7853 0.0983186 0.0942857 35.879
5 2.66051 2.82611 0.104588 0.0592063 47.6442
6 2.64653 2.84772 0.110235 0.0937037 59.3844
7 2.63512 2.81853 0.111765 0.0592063 71.0073
8 2.61773 2.84415 0.120295 0.0831217 82.6477
9 2.60187 2.80639 0.125265 0.091164 94.1596
10 2.59428 2.798 0.130412 0.0944974 105.526
11 2.57489 2.82496 0.132566 0.071164 116.915
12 2.5647 2.84402 0.134647 0.096455 128.34
13 2.54531 2.91482 0.143324 0.0850794 139.941
14 2.53773 2.83752 0.148353 0.0897884 151.488
15 2.52841 2.81961 0.152006 0.0725397 162.79
16 2.51507 2.96342 0.152412 0.071164 174.238
17 2.50024 2.97278 0.158618 0.103704 185.85
18 2.48458 3.03544 0.165074 0.0844974 197.423
19 2.46567 2.98729 0.169794 0.111746 209.066
20 2.46163 2.97408 0.168559 0.081164 220.849
21 2.43796 3.05378 0.177029 0.0878307 232.583
22 2.42934 2.86844 0.181268 0.075873 244.434
23 2.39571 2.9371 0.191206 0.096455 256.263
24 2.37371 2.95642 0.197971 0.091746 268.319
25 2.35578 2.96039 0.207345 0.0978307 280.227
26 2.32705 3.01686 0.216471 0.091746 292.061
27 2.3103 3.077 0.221088 0.0931217 304.246
28 2.26667 3.06368 0.233706 0.106455 316.494
29 2.23368 3.05979 0.248378 0.135661 328.63
30 2.19393 3.45029 0.263412 0.0878307 340.724
31 2.16578 3.47368 0.269529 0.0931217 352.725
32 2.13084 3.31725 0.281765 0.0992063 364.935
33 2.09286 3.59374 0.2959 0.0925397 377.033
34 2.04235 3.6446 0.312088 0.107037 389.009
35 1.99226 3.73125 0.329559 0.0897884 401.031
36 1.95377 3.71884 0.343717 0.109206 412.944
37 1.90421 3.77256 0.360529 0.0978307 424.951
38 1.86084 4.0408 0.377588 0.10254 436.903
39 1.7942 4.35645 0.398176 0.105079 448.987
40 1.74267 4.43788 0.415752 0.0672487 460.879
というわけで JRA のデータを使って競馬予想を試してみました。データの選び方やニューラルネットワークのモデルによっては精度が上がる気もするのでいろいろ試してみようと思います。
今回試したコードはこちら(試行錯誤していたのでコメントアウトしてるコードがあったりしますが。。)
https://github.com/takecian/HorseRacePrediction