NMFは次元削減の手法であり、レコメンドの精度を高めることができるといわれています。
機会学習ライブラリのscikit-learnでもNMFを簡単に使うことができます。
今回は、具体例を用いて試して、NMFを直感的に理解することが目的です。
「Matrix Factorizationとは」という記事がわかりやすいです。
NMFとは
レコメンドとしてのMatrix Factorizationについてざっくりと理解するには、英語ですが、以下の資料がわかりやすいです。
Matrix Factorization Techniques For Recommender Systems
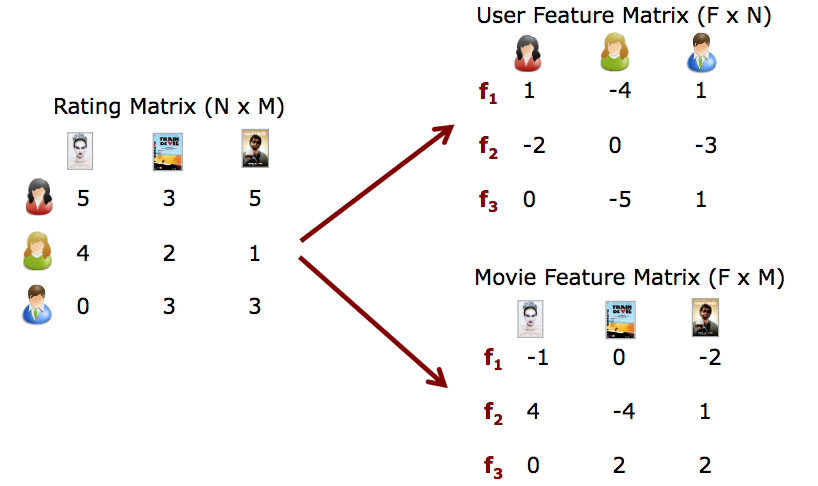
このスライドにある図を引用しながら軽くイメージを説明します。
NMFの手法が一躍有名になった、Netflix Prizeを想定し、ユーザーとその人がどの動画に何点の評価をつけたかを表す行列が与えられるとします(左のRating Matrixという行列)。ユーザーが動画を評価した場合は1から5でレーティング付けが、評価しなかった場合は0が入力入っています。0が入っているのがこの問題の肝で、この0の本当の値を予測します。
このRating Matrixを「特徴×ユーザー」、「特徴×映画」という2つの行列に分解します。
すごくすごくおおざっぱにいうと、うまく行列分解をする手法がNMFになります。
NMFの定式化
$\mathbf{R}$:Rating Matrix
$\mathbf{P}$:User Feature Matrix
$\mathbf{Q}$:Movie Feature Matrix
としたとき、$\mathbf{R}$と $\mathbf{P} \times \mathbf{Q}^T$ の誤差が小さくなるように分解します。
\mathbf{R} \approx \mathbf{P} \times \mathbf{Q}^T = \hat{\mathbf{R}}
誤差は$e_{ij}^2$のように表すことができます。
e_{ij}^2 = (r_{ij} - \hat{r}_{ij})^2 = (r_{ij} - \sum_{k=1}^K{p_{ik}q_{kj}})^2
ただし、近似した$ \hat{\mathbf{R}} $の要素は以下
\hat{r}_{ij} = p_i^T q_j = \sum_{k=1}^k{p_{ik}q_{kj}}
0.5 * ||X - WH||_Fro^2
+ alpha * l1\_ratio * ||vec(W)||_1
+ alpha * l1\_ratio * ||vec(H)||_1
+ 0.5 * alpha * (1 - l1\_ratio) * ||W||_Fro^2
+ 0.5 * alpha * (1 - l1\_ratio) * ||H||_Fro^2
||A||_Fro^2 = \sum_{i,j} A_{ij}^2 (Frobenius norm)
||vec(A)||_1 = \sum_{i,j} abs(A_{ij}) (Elementwise L1 norm)
scikit-learnでの実装
簡単にかけます。
例えば、レーティングの行列をR、特徴の次元を2とした場合のコードは以下の通り
from sklearn.decomposition import NMF
model = NMF(n_components=2, init='random', random_state=0) # n_componentsで特徴の次元を指定
P = model.fit_transform(R) # 学習
Q = model.components_
具体例
Rを次のような5×4行列だとします。この行列の数字は、このサイトで利用されている例を参考にしました。
| D1 | D2 | D3 | D4 | |
|---|---|---|---|---|
| U1 | 5 | 3 | - | 1 |
| U2 | 4 | - | - | 1 |
| U3 | 1 | 1 | - | 5 |
| U4 | 1 | - | - | 4 |
| U5 | - | 1 | 5 | 4 |
from sklearn.decomposition import NMF
import numpy as np
# 0の部分は未知
R = np.array([
[5, 3, 0, 1],
[4, 0, 0, 1],
[1, 1, 0, 5],
[1, 0, 0, 4],
[0, 1, 5, 4],
]
)
# 特徴の次元kを1から3まで変えてみる
for k in range(1,4):
model = NMF(n_components=k, init='random', random_state=0)
P = model.fit_transform(R)
Q = model.components_
print("****************************")
print("k:",k)
print("Pは")
print(P)
print("Q^Tは")
print(Q)
print("P×Q^Tは")
print(np.dot(P,Q))
print("R-P×Q^Tは")
print(model.reconstruction_err_ )
出力結果は以下のようになります。
****************************
k: 1
Pは
[[ 0.95446553]
[ 0.64922245]
[ 1.12694515]
[ 0.87376625]
[ 1.18572187]]
Q^Tは
[[ 1.96356213 1.0846958 1.24239928 3.24322704]]
P×Q^Tは
[[ 1.87415238 1.03530476 1.18582729 3.09554842]
[ 1.27478862 0.70420887 0.8065935 2.10557581]
[ 2.21282681 1.22239267 1.40011583 3.65493896]
[ 1.71569432 0.94777058 1.08556656 2.83382232]
[ 2.32823857 1.28614754 1.47314 3.84556523]]
R-P×Q^Tは
7.511859871919941
****************************
k: 2
Pは
[[ 0. 1.69547254]
[ 0. 1.13044637]
[ 1.38593123 0.42353044]
[ 1.08595617 0.3165454 ]
[ 2.01891156 0. ]]
Q^Tは
[[ 0. 0.32199795 1.40668938 2.58501889]
[ 3.09992487 1.17556787 0. 0.85823043]]
P×Q^Tは
[[ 5.25583751 1.99314304 0. 1.45510614]
[ 3.50429883 1.32891643 0. 0.97018348]
[ 1.31291255 0.9441558 1.94957474 3.94614513]
[ 0.98126695 0.72179626 1.52760301 3.0788861 ]
[ 0. 0.65008539 2.83998144 5.21892451]]
R-P×Q^Tは
4.2765298341191516
****************************
k: 3
Pは
[[ 0.08750151 2.03662182 0.52066139]
[ 0. 1.32090927 0.59992585]
[ 0.04491053 0.44753619 3.4215759 ]
[ 0. 0.3221337 2.75625987]
[ 2.6249395 0. 0.91559966]]
Q^Tは
[[ 0. 0.38636917 1.90213535 1.02176621]
[ 2.62017626 1.02934221 0. 0.08629708]
[ 0. 0.02388804 0. 1.43875694]]
P×Q^Tは
[[ 5.33630814 2.14262626 0.16643971 1.0142658 ]
[ 3.4610151 1.37399871 0. 0.97713811]
[ 1.17262369 0.55975468 0.08542591 5.00732522]
[ 0.84404708 0.39742747 0. 3.99338722]
[ 0. 1.03606758 4.99299022 3.99939987]]
R-P×Q^Tは
1.8626938982246695
観測行列Rは、5×4 の行列でした。
kをいろいろ変えて試した時に、Pが5×kの行列、Q^Tがk×4の行列になっていることがわかると思います。
また、P×Q^T では、Rでは0であったところが推測されており、例えばk=2の場合は以下のような$ \hat{\mathbf{R}} $が完成しています。(太字が予測された部分)
| D1 | D2 | D3 | D4 | |
|---|---|---|---|---|
| U1 | 5.25 | 1.99 | 0. | 1.45 |
| U2 | 3.50 | 1.32 | 0. | 0.97 |
| U3 | 1.31 | 0.94 | 1.94 | 3.94 |
| U4 | 0.98 | 0.72 | 1.52 | 3.07 |
| U5 | 0. | 0.65 | 2.83 | 5.21 |
kをどの値にするかは難しい問題であり、入力データ(R)に依存するとされています。
- kを大きくすれば、R-P×Q^T は小さくなり、モデルの複雑度は高くなる。
- 逆にkを小さくすれば、R-P×Q^T は大きくなり、モデルの複雑度は低くなる。
今回の場合、どのkがよいと判断するにはどうすればよいのでしょうか。(ご存じの方ご教授ください)
リンク
-
scikit learn リファレンス
-
Matrix Factorizationとは(わかりやすいqiita)
-
Matrix Factorization Techniques For Recommender Systems(わかりやすいスライド