はじめに

最近「Pythonによる制御工学入門」という本を読みました。その中で出てくるPython-Controlってやつを試してみたいなということで、周波数制御のシミュレーションをしてみようと思います。制御とタイトルに入ってますが、電力工学のお話がメインとなります。

・電力系統と周波数制御の解説
・Python-Controlを使ってみる

という内容になります。

周波数とは

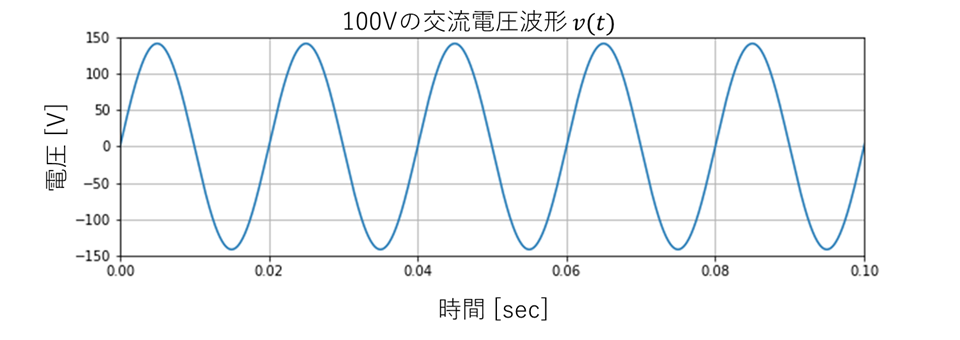
私たちが家庭で使っている100Vの電気は、常に100Vとなっているわけではなく下の図のように一定周期で振動しています。この時、電圧の時間変化は
$$v(t) = 100\sqrt 2 \sin(2\pi f t)　 [\rm{V}]$$
と表されます。ここで、$f\ $は周波数と呼ばれ、１秒間に何回振動するかを表しています。そして、この周波数というの東日本では50Hz、西日本では60Hzとなっています。

電気を使う側にとっては、電気の周波数というのは50 or 60Hzで一定のものとして扱うことが多いです。しかし実際の周波数は常に変動していて周波数が大きく変化すると電気機器に悪影響を及ぼす可能性があります。そこで、電力系統の運用者(つまり電力会社)は周波数が大きく変動しないよう制御する必要があります。

需給バランスと周波数の関係

電力系統の需要と供給

なぜ周波数が変動するのかを説明する前に、まず電力系統について簡単に説明します。
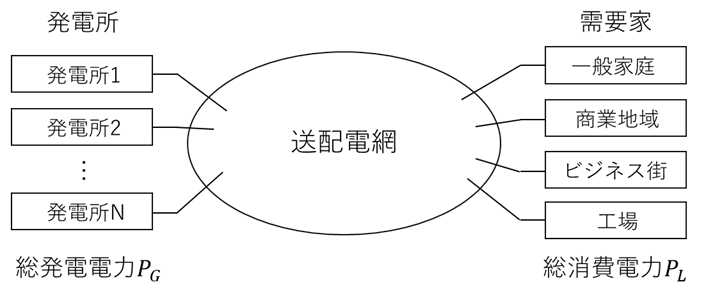
電力系統は、電力を供給する発電所、電力を消費する需要家、そしてそれらをつなぐ送配電網で構成されます。
電力系統の重要な性質として、供給する電力$P_G$と消費する電力$P_L$が常に一致していなければならない「同時同量」という原則があります（電気は貯めることが難しいので）。しかし電気を使う側(需要家)は好きな時に好きなだけ電気を使いたいので、同時同量を実現するには発電所が常に発電電力を消費電力に合わせる必要があります。

では、どのようにして発電所側は発電電力を消費電力に合わせるのか。すべての需要家の消費電力をリアルタイムで把握することはできません。そこで重要となってくるのが周波数制御になります。

発電機の動揺方程式

　発電所の種類は、火力・水力・原子力発電があります。最近は太陽光発電とか風力発電とか増えてきてますが今回は考えません。これらの発電方法は、いかにして回転エネルギー(機械エネルギー)を得るかという部分が異なるだけで、機械エネルギーから電気エネルギーに変換する部分は全て一緒で、「同期発電機」が使われています。

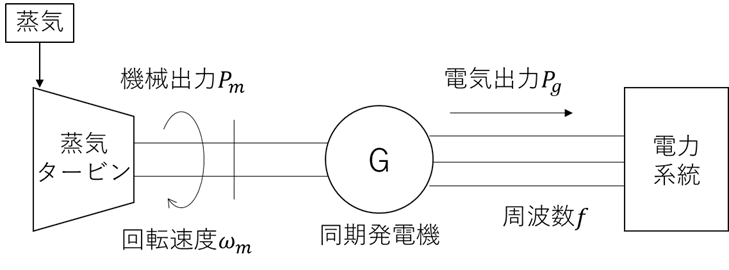
図のように、蒸気タービンの同軸上に発電機を設置することでタービンの機械出力を電気エネルギーに変換します。この時、回転子の回転速度$\omega_m\ [\rm{rad/s}]$と発電機によって誘起される電圧の周波数$f\ [\rm{Hz}]$には以下の関係が成り立ちます。
$$\omega_m=2\pi f/p$$
ここで、$p$は極対数と呼ばれるもので発電機によって固定の値(火力であれば$p=1$が多い)になります。したがって、電気的な周波数と発電機・タービンの回転速度は同等のものになります。周波数というのは電力系統全体で同じ値であるため、系統に接続されている発電機はすべて同じ速度で回転します。つまり発電機の回転数を制御することは、電力系統全体の周波数を制御することと同じことになります。
　発電機の回転速度(=周波数)の変化は、以下の動揺方程式で表されます。
$$M\frac{df}{dt}=P_m-P_g$$
ここで、$M$は慣性定数と呼ばれ、回転体の慣性モーメントのようなパラメータです。また、機械出力$P_m$の値は蒸気の流量などによって決まる制御可能な値ですが、電気出力$P_g$は電力系統の電力需要$P_L$によって決まります(系統の損失を無視すれば$P_g=P_L$)。この動揺方程式から、以下のことが言えます。

$P_m>P_g$のとき、周波数は上昇(供給過剰)
$P_m=P_g$のとき、周波数は一定(需給がバランス)
$P_m<P_g$のとき、周波数は低下(供給不足)

つまり、電力系統の周波数を測定し、周波数が上昇すれば発電機の出力を下げ、周波数が低下すれば発電機出力を上げる必要があります。周波数制御とは、需給バランスと周波数の関係を利用したフィードバック制御になります。

周波数制御の概要

ブロック図

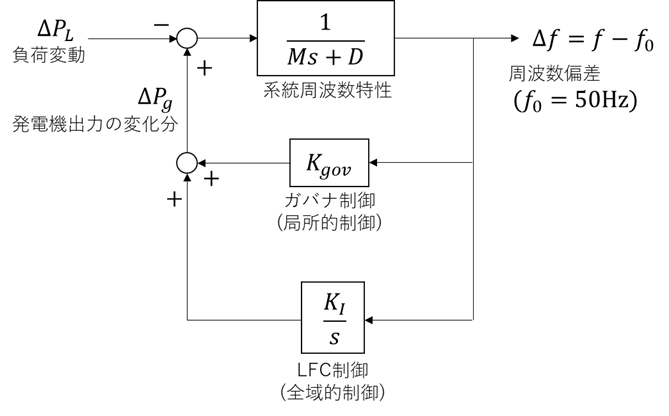
今回は、電力系統全体の発電機を1台に集約した場合を考えます。周波数制御のブロック図は以下のようになります。発電機出力と負荷との差分が周波数変動に影響を与えます。図の系統周波数特性というのは、発電機の慣性に加え、負荷の周波数特性も考慮されたものです。フィードバックのループは主に2種類で、局所的制御ループと全域的制御ループがあります。

局所的制御

局所的制御ループでは、発電機のガバナ(調速機)が周波数を計測して、周波数の偏差に応じてタービンに流入する蒸気の量を調整します。これにより、負荷が変動したときでも需給バランスを維持することができます。
ただし、局所的制御のみだと需給バランスは維持できても、周波数は定常偏差が生じて$50\rm{Hz}$からずれた値に収束してしまいます。

全域的制御

全域的制御は、中央給電指令所という発電所を管理している場所からの制御となります。局所的制御のみでは周波数偏差が出てしまいますが、ここでは積分制御を使用して周波数が$50\rm{Hz}$に戻るように各発電機に指令を出します(今回は発電機1台)。

また、今回は単純な積分制御を利用していますが、実際の系統では発電機ごとの速度特性や燃料コストがさまざまであるためそれらを総合的に考慮して出力を決定しています。

Python-Controlを使ってみる

Python-Controlの使い方はこの記事を参考にしました。
PythonControlで正弦波に対する応答を求める。

伝達関数を計算

それでは、Pythonで負荷変動に対する周波数の変動をシミュレーションしたいと思います。サンプルコードは最後にまとめて載せます。
まずは、下の図のように制御ブロックを単純化して一つの伝達関数で表します。Python-Controlを用いることで伝達関数の扱いが容易になります。

条件設定

シミュレーション時間は100秒として、刻みは0.01秒とします。負荷変動は、シミュレーション開始10秒後に10%上昇するという想定です。

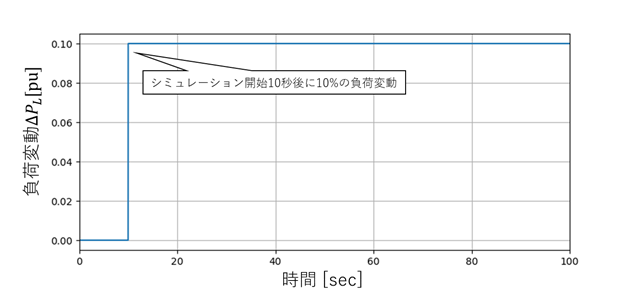
シミュレーション

負荷変動を与えたときの、周波数偏差の時間変化を示します。
まずは、局所的制御のみの場合($K_I=0$)です。定常偏差があることがわかります。

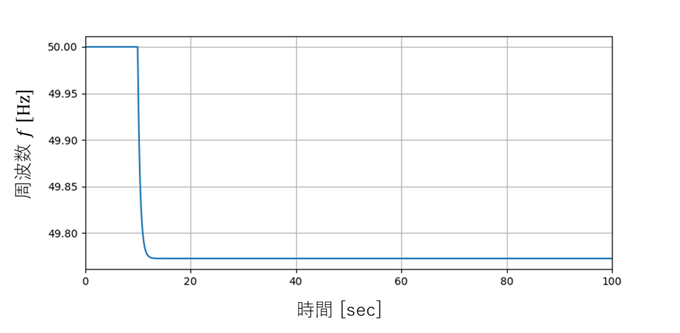
次に、全域的制御を加えた場合です。きちんと50Hzに戻るようになりました。

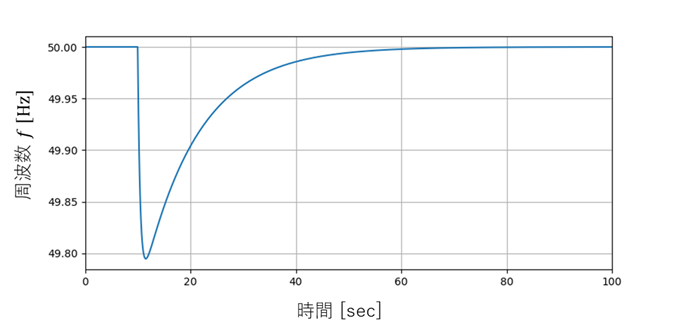
このように、電力系統では常に周波数を監視し50Hzもしくは60Hzを維持できるように発電所の出力を調整し続けています。ただし、近年増加している再生可能エネルギー（風力や太陽光）の電源は出力を制御することが難しく、周波数制御能力を低下させる要因になっています。増加し続ける再エネ電源に対応するため、電力会社さんも苦労しているみたいです...。

さいごに

本当は、2018年9月の北海道ブラックアウトの再現シミュレーションを組んでみたかったのですが、複雑でよくわかりませんでした。なので今回は周波数制御の一番簡単なやつを試してみました。ちょっとずつできることを増やしていきたいです。

興味がある方はこの資料を読んでみてください。ブラックアウト直前の周波数変動とかが載ってます。
ブラックアウトとはどういう現象か - 電気学会

サンプルコード

import numpy as np
from control.matlab import *
import matplotlib.pyplot as plt


def main():
    # パラメータ設定
    M = 10  # 慣性定数
    D = 2  # ダンピング
    K_gov = 20  # 比例制御ゲイン
    K_I = 2  # 積分制御ゲイン

    # 伝達関数の設定
    System_frequency = tf(1, [M, D])  # 系統周波数特性
    Governor = tf(K_gov, 1)  # ガバナ制御ブロック
    LFC = tf(K_I, [1, 0])  # LFC制御ブロック
    G = - feedback(System_frequency, Governor + LFC)  # システム全体の伝達関数

    # シミュレーション設定
    T = np.arange(0, 100, 0.01)  # 0~100秒
    dPL = np.array([0 if t < 10 else 0.1 for t in T])  # 負荷変動の設定(ステップ変動)

    # 計算
    df, T, _ = lsim(G, dPL, T)

    # プロット
    plt.figure(figsize=(9, 4))
    plt.plot(T, dPL)  # 負荷変動
    plt.grid()
    plt.xlim(0, 100)

    plt.figure(figsize=(9, 4))
    plt.plot(T, (df+1)*50)  # 周波数偏差
    plt.grid()
    plt.xlim(0, 100)


if __name__ == '__main__':
    main()
    plt.show()

Pythonで周波数制御のシミュレーションやってみる