【signate】お弁当の需要予測チュートリアル 〜重回帰分析編〜

signateと呼ばれる日本版kaggleのようなサイトで、勉強用に提供されているデータを使用して、お弁当の需要予測をしていきたいと思います。

コンペの概要

千代田区四番町のとある会社のカフェフロアで販売されているお弁当の販売数を予測するモデルを作成していただきます。
データの期間は、お弁当の販売を開始した 2013年11月18日 から 2014年11月30日 まで（土日祝を除く平日）です。
学習用データ期間：2013年11月18日 ～ 2014年 9月30日
検証用データ期間：2014年10月 1日 ～ 2014年11月30日

使用しているデータはこちらにあります。

この記事の概要

お弁当の需要予測を重回帰分析を用いて実践してみます。
→単回帰分析で実践した記事はこちら。
最後には、signateへデータを提出し、単回帰分析（別記事）と重回帰分析でどの程度、精度に差が出るのかを検証してみます。

重回帰分析（説明変数を曜日と気温で）

重回帰分析とは、説明変数が2つ以上ある場合の回帰分析のことです。
今回は、説明変数を曜日と気温で実践します。

大枠の手順は単回帰分析の時と同様なので、こちらの記事をご覧ください。

1. データの準備（データセットの読み込み）

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegression as LR # 線形回帰のモデル
%matplotlib inline

train = pd.read_csv('train.csv') # 学習データの読み込み
test = pd.read_csv('test.csv') # 検証データの読み込み
sample = pd.read_csv('sample.csv', header=None) # 提出用サンプルデータの読み込み

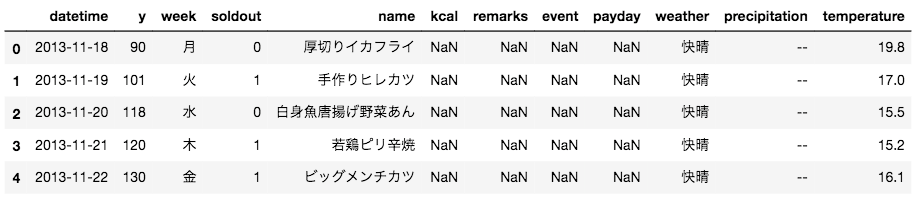
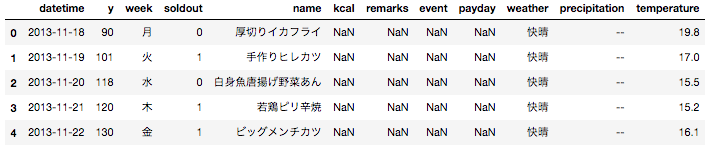
# データ確認
train.head()

今回はweekとtemperatureを使用しますが、
weekは数値項目ではないため、このままだと使えません
このようなデータをカテゴリデータ（例：性別、出身国、曜日…）と呼びます。

このデータをダミー変数化（one-hot表現とも言う）して学習に使えるようにする必要があります。
ダミー変数について詳しく知りたい方はこちらやこちらを参考にしてみてください。

一度、各曜日がどれくらい存在しているのか確認してみます。

train['week'].value_counts()
#> 水    43
#> 木    43
#> 火    41
#> 金    41
#> 月    39

５種類の曜日が設定されていることが分かりました。
では、ダミー変数化してみます。

# 説明変数として使用する week と temperature をダミー変数化しながら X_trainに設定
X_train = pd.get_dummies(train[['week', 'temperature']])

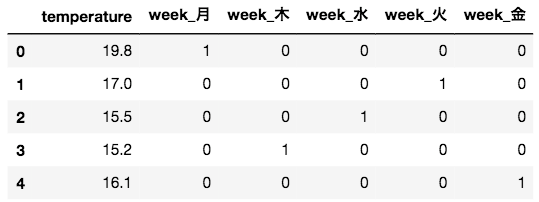
X_train.head()

見て分かるように、get_dummies関数は、引数に複数のカラムを与えても、ダミー変数化できるものだけ（今回だと曜日のみ）を良い具合に処理してくれます。

目的変数も用意しておきます。

y_train = train['y']

2. モデルの準備

冒頭でimportしたLinearRegressionを使ってモデルの定義をします。

# モデルの定義
model = LR()

3. モデルの作成

重回帰モデルを生成します。

model.fit(X_train, y_train)

学習後モデルの傾きや切片を確認してみます。

model.coef_ #傾き
# > array([-2.53878074,  8.26339936, -9.47240196, -2.02873774,  1.85251984, 1.38522051])

model.intercept_ #切片
# > 135.69119841401601

傾きが複数個あるのは、それぞれ、気温に関する係数、月曜日に関する係数…となっているからです。

4. 予測

では、実際に売上数を予測してみます。
予測にはpredict関数を使用します。

# 検証用データ
X_test = pd.get_dummies(test[['week', 'temperature']])

# 予測
pred = model.predict(X_test)
print(pred)
# > [ 82.37908978  65.54193684  64.21341177  89.37081192  81.43666396
# >   74.5088695   69.09622987  70.81424168  69.5043945   94.05748117
# >   78.99747474  78.68446197  83.27773815  86.26034736  94.31135925
# >   88.89871962  89.60121914  86.32427504  89.05300617  83.90235823
# >   76.45869401  89.34734106  89.56076232  93.04196888  77.4742063
# >   86.0469261   90.13244614 100.22364142  97.10401806  76.71257208
# >   96.96368327 107.65003323  96.66934838  95.83462769  99.56159871
# >   99.24858594 108.60161785 110.30567789  87.88320732  98.23307364]

5. 評価

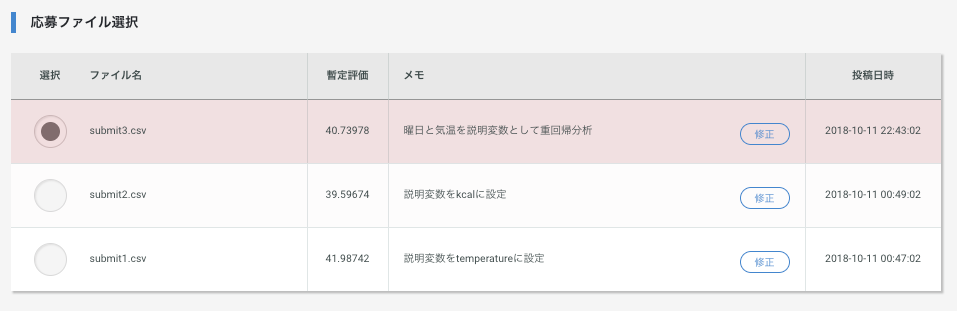
signateに提出してモデルを評価するためにCSV出力を行い、提出してみます。

sample[1] = pred
sample.to_csv('submit3.csv', index=None, header=None)

説明変数を多く使用してモデルを構築したにもかかわらず、単回帰分析のときよりも精度が落ちています。
（今回の評価関数は数値が低ければ低いほど精度が良いことを表しています）

今回は曜日（week）と気温（temperature）を説明変数としましたが、
この選択があまりよくなかったようです。

では、どのようにして精度をあげればよいのか。
考えていきましょう。

特徴量抽出

特徴量とは、今まで説明してきた説明変数と同じ意味です。
予測精度を向上させるために、特徴量はとても重要なポイントになります。

予測精度を向上させるためにはいくつか手法がありますが、今回は下記2点を紹介します。

• 特徴量を作る
• 特徴量を選ぶ

特徴量を作るとは

与えられたデータや外部データを加工し、予測の手がかりとなりそうな新しい特徴を作ることです。

ex.1）基本統計量をつくる
Aさんのテストの点数とBさんのテストの点数があった時に、二人のテストの平均点を3つ目の特徴量として新たに定義します

ex.2)データを集約する
年齢というカラムがあったときに、それを20代30代４０代のように集約し、新たな特徴量として定義します

特徴量を選ぶとは

特徴量は多ければ多いほど良い、ということではないです。
→過学習のリスクがある

重要な特徴量を選択することが大切。
下記に特徴量選択の手法をあげてみます。
詳しく知りたくなった方はgoogle先生に聞いてみてください。

• 単変量解析
  目的変数と各特徴量を1対1で確認し、取捨選択する

• モデルベース選択
  モデルにとっての各変数の重要度を算出し、取捨選択する

• 反復選択
  特徴量を増減させながらモデルを生成し、良い特徴量を探索する

上記を踏まえて、もう一度モデルを構築し直してみましょう。
重複する補足などは端折ります。

重回帰分析（説明変数を年と月で）

1. データの準備（データセットの読み込み）

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
from sklearn.linear_model import LinearRegression as LR

train = pd.read_csv('train.csv') # 学習データの読み込み
test = pd.read_csv('test.csv') # 検証データの読み込み
sample = pd.read_csv('sample.csv', header=None) # 提出用サンプルデータの読み込み

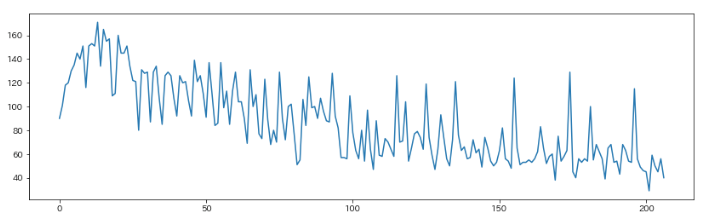
ここで、y(売り上げ)のグラフをプロットしてみます。

train['y'].plot(figsize=(14,4))

x軸は時間、y軸は売り上げ

グラフを見ると、時間が経つにつれて売り上げが落ちてきていることが分かりますが、
今までの手法では、時間軸を持った特徴量を選択していませんでした。

よって、時間軸をもった特徴量として、年と月を選択し、重回帰分析を実践してみましょう。

trainのデータを再確認

train.head()

datetimeのカラムを、年と月に分割し、新しい特徴量として定義する。

# datetimeを分割して設定
train['year'] = train['datetime'].apply(lambda x : x.split('-')[0])
train['month'] = train['datetime'].apply(lambda x : x.split('-')[1])
test['year'] = test['datetime'].apply(lambda x : x.split('-')[0])
test['month'] = test['datetime'].apply(lambda x : x.split('-')[1])

# 新規で定義したカラムのデータ型はobject型になってしまうため、int型へ変換する
train['yaer'] = train['year'].astype(np.int)
train['month'] = train['month'].astype(np.int)
test['yaer'] = test['year'].astype(np.int)
test['month'] = test['month'].astype(np.int)

新しい特徴量を定義したあとのX_train
yearとmonthが新しく特徴量として追加されているのが分かります

最後に特徴量を設定します。

X_train = train[['year', 'month']]
X_test = test[['year', 'month']]
y_train = train['y']

2. モデルの準備

冒頭でimportしたLinearRegressionを使ってモデルの定義をします。

# モデルの定義
model1 = LR()

3. モデルの作成

重回帰モデルを生成します。

model1.fit(X_train, y_train)

学習後モデルの傾きや切片を確認してみます。

model1.coef_ #傾き
# > array([-104.0107109 ,   -7.41004428])

model1.intercept_ #切片
# > 209594.15656370917

4. 予測

pred = model1.predict(X_test)

5. 評価

signateに提出してモデルを評価するためにCSV出力を行い、提出してみます。

sample[1] = pred
sample.to_csv('submit4.csv', index=None, header=None)

大幅に精度がよくなりました！

もう少し精度をあげたい

さて、さらに精度をあげるべく、別の特徴量は作れないか考察してみます。

予測と実際のデータを比較してみる

実際の売り上げデータyと、先で作成したモデルmodel1が予測したデータを比較すれば、
どのデータで予測が大きく外れているか分かるはずです。

どうやれば良いかと言うと、X_trainに対してmodel1で予測を行えば、実際の売り上げyがわかっているため、その差を比較できそうです。
次に、X_trainに対する予測値と、実際の売り上げyとを引き算することで、どの日が大きく予測を外していたかを確認します。

まず、model1とX_trainを使って、X_trainに対する予測値を求めてみます。

pred = model1.predict(X_train)

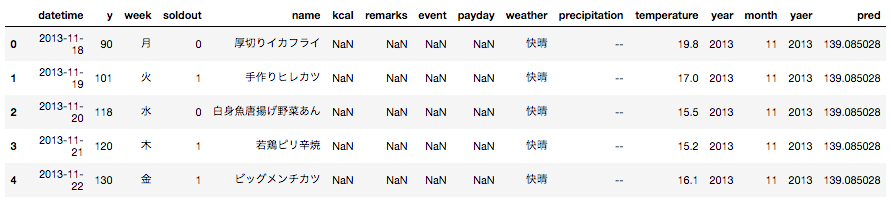
# predをtrainの新たなカラムpredとして代入
train['pred'] = pred
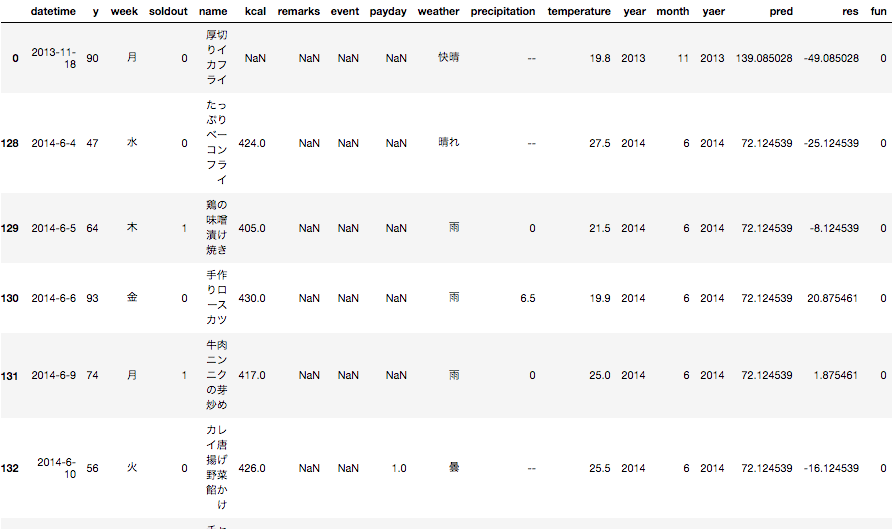
train.head()

新しくpredカラムが追加されている

# trainのyとpredを引き算した結果をtrainの新たなカラムresとして代入
train['res'] = train['y'] - train['pred']

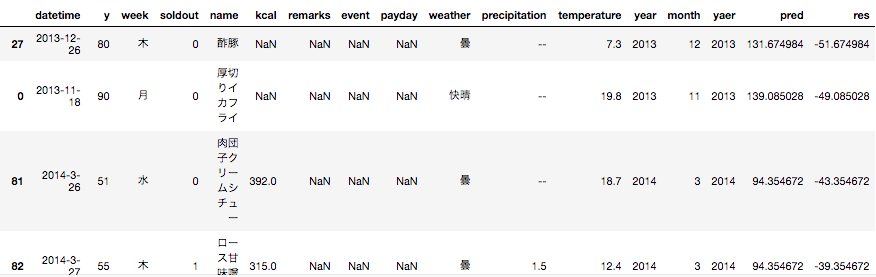
# ソートして中身を確認
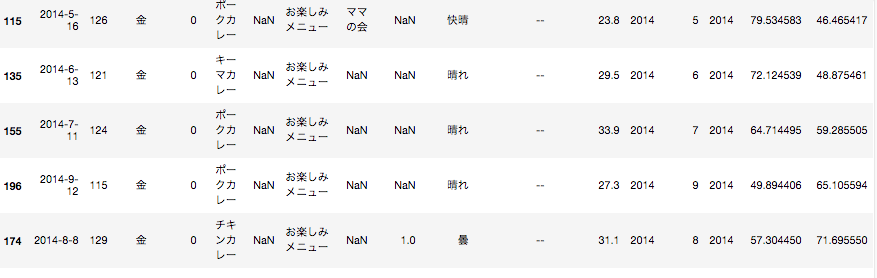
train.sort_values(by='res')

マイナス方向へズレが大きいもの

プラス方向へズレが大きいもの

上記より、予測が大きく外れていたものから共通する要素が見つけられれば、その要素を加えることで更に精度が良いモデルを作れる可能性がありそうです。

データを見てみると、プラス方向へズレが大きいデータはremarksカラムにお楽しみメニューという文字列が設定されていることが分かると思います。
これでうまく特徴量を作成することができれば、プラス方向へズレが大きいデータを減らすことができそうですね。

早速実践していきましょう。

まず、値が「お楽しみメニュー」であれば１、そうでなければ0とする関数を作成します。
そして、その関数を用いて新たなカラムfunを作ってみます。

# 関数
def jisaku1(x):
    if x == 'お楽しみメニュー':
        return 1
    else:
        return 0

train['fun'] = train['remarks'].apply(lambda x : jisaku1(x))
test['fun'] = test['remarks'].apply(lambda x : jisaku1(x))

データを確認してみましょう

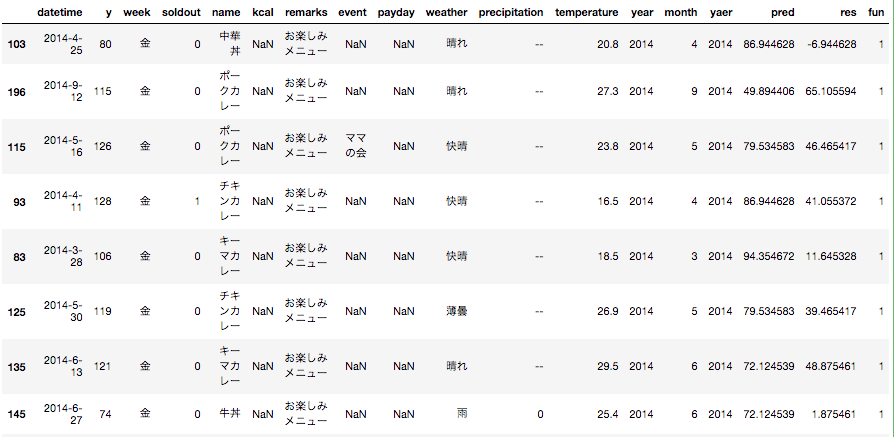
train.sort_values(by='fun', ascending=False)[:10]
train.sort_values(by='fun', ascending=True)[:10]

ascending=Falseの上位データ

ascending=Trueの上位データ

確かに、お楽しみメニューデータのfunカラムに1が設定されています。

ここで、今までの特徴量yearとmonthに加え、funとtemperatureも特徴量として、重回帰分析を実践していきたいと思います。

その後、今まで通りCSV出力して、signateへ提出しみたいと思います！

X_train = train[['yaer', 'month', 'fun', 'temperature']]
X_test = test[['year', 'month', 'fun', 'temperature']]

model2 = LR()

model2.fit(X_train, y_train)

pred2 = model2.predict(X_test)
sample[1] = pred2
sample.to_csv('submit5.csv', index=None, header=None)

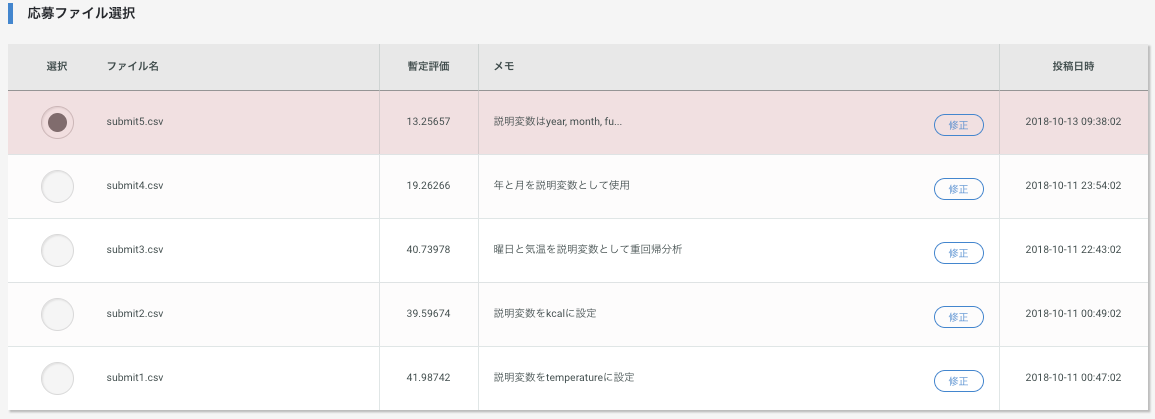
いざ提出・・・

13.25657という今までで一番良いスコアがつきました！

ここまでやってみると、いかに特徴量が大切かがわかったと思います。

おわり