【signate】お弁当の需要予測チュートリアル 〜単回帰分析編〜

signateと呼ばれる日本版kaggleのようなサイトで、勉強用に提供されているデータを使用して、お弁当の需要予測をしていきたいと思います。

コンペの概要

千代田区四番町のとある会社のカフェフロアで販売されているお弁当の販売数を予測するモデルを作成していただきます。
データの期間は、お弁当の販売を開始した 2013年11月18日 から 2014年11月30日 まで（土日祝を除く平日）です。
学習用データ期間：2013年11月18日 ～ 2014年 9月30日
検証用データ期間：2014年10月 1日 ～ 2014年11月30日

使用しているデータはこちらにあります。

この記事の概要

お弁当の需要予測を単回帰分析を用いて実践してみます。
→重回帰分析を用いるパターンは別記事にしたいと思います。
最後には、signateへデータを提出し、単回帰分析と重回帰分析（こちら）でどの程度、精度に差が出るのかを検証してみます。

モデリングの手順

まず初めに、一般的（？）なモデリングの手順を書いておきます。

1. データの準備
   　- 欠損値などの前処理とか
   　- 特徴量抽出（精度に影響する変数を選定）
2. モデルの準備（今回は単回帰モデルと重回帰モデルを使用する）
3. モデルの作成
4. 予測
5. 評価

単回帰分析（説明変数を温度で）

まずは、温度から需要予測を立ててみます。
（その日の温度が、お弁当の売り上げに影響を与えているのではないか？という予測を立てた上で温度を使用します）

1. データの準備（データセットの読み込み）

冒頭で説明したデータセットをダウンロードし、プログラムと同じフォルダに配置後、以下コードを実行しデータフレームとして読み込みます。

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegression as LR # 線形回帰のモデル
%matplotlib inline # notebook上でグラフを表示するおまじない

train = pd.read_csv('train.csv') # 学習データの読み込み
test = pd.read_csv('test.csv') # 検証データの読み込み
sample = pd.read_csv('sample.csv', header=None) # 提出用サンプルデータの読み込み

データの中身を確認してみます。

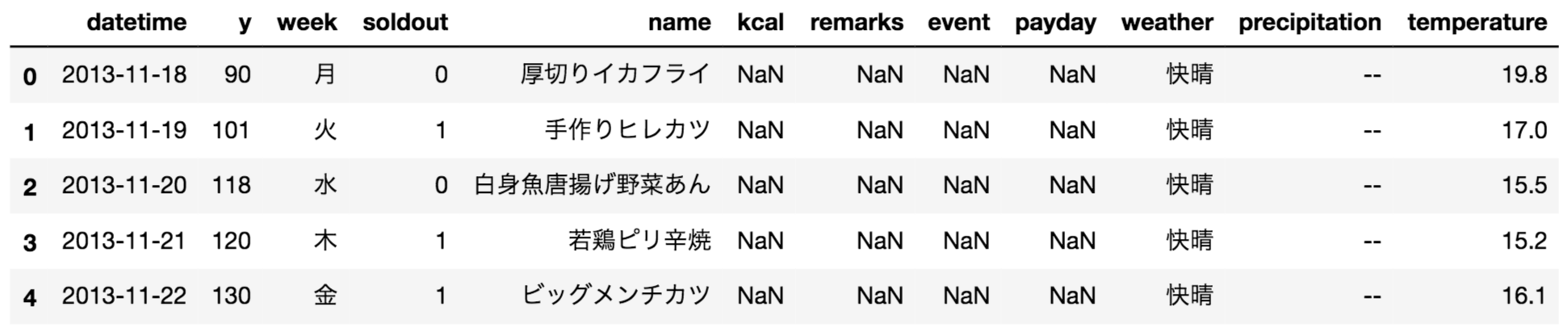
train.head() #先頭データ
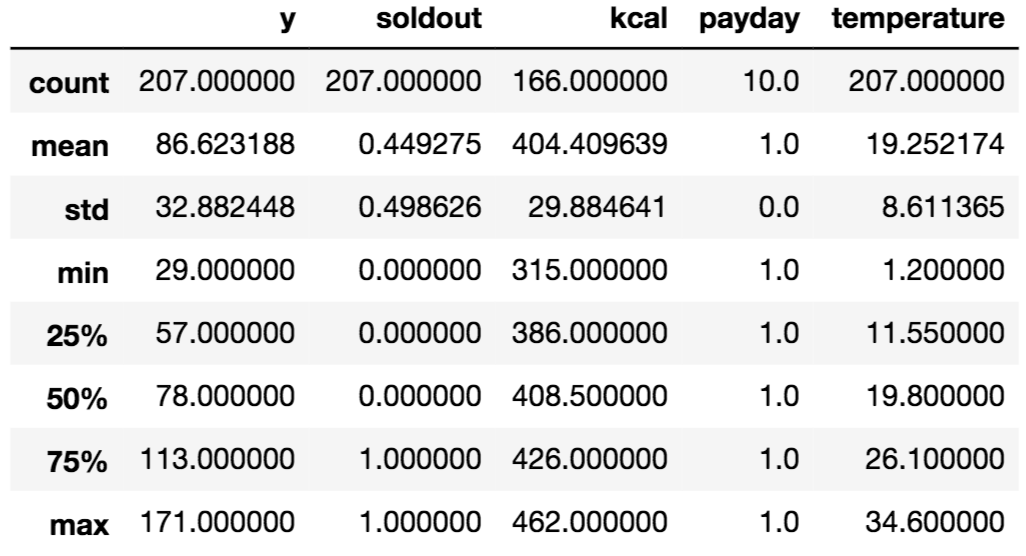
train.describe() #基礎統計量

先頭データ

基礎統計量

基礎統計量を見てみると、kcalには欠損値があることが分かりますね。

このセクションでは、temperature （温度）を説明変数として、単回帰分析を行います。
目的変数はy （その日の売り上げ）です。
（次セクションで、kcal（カロリー）を説明変数として単回帰分析してみた結果も載せています）

# 学習用データ
# 説明変数に "temperature (温度)" を利用
X_train = train['temperature']
# 目的変数に "y (売り上げ個数)" を利用
y_train = train['y']

# 検証用（予測用）データ
X_test  = test['temperature']

そして、データの形状を変換します。（単回帰分析ではこの変換が必要です）
今のままだと下記のような形状なので、これを1行1列の配列に変換します。

X_train.head()
# > 0    19.8
# > 1    17.0
# > 2    15.5
# > 3    15.2
# > 4    16.1
# > Name: temperature, dtype: float64

X_train.shape
# > (207,)

変換

X_train = X_train.values.reshape(-1,1)
X_test = X_test.values.reshape(-1,1)

reshape(行,列)と指定することで、指定した配列へと変換されます。
ここでは行に-1を指定して、行数は元の形状から推測するようにしています。
少しわかりにくいですが、公式ドキュメントには下記のように記載されています。

新しい形状は、元の形状と互換性がなければなりません。整数の場合、結果はその長さの1次元配列になります。 1つの形状寸法は-1とすることができる。この場合、値は配列の長さと残りの次元から推測されます。

また、こちらの記事で-1について詳しく解説されていますので、よければ参考になさってください。

なお、変換後の形状はnumpyのndarray型になります。
dataframeではないので、head()関数は使えません。

X_train[:5]
# > array([
# >    [19.8],
# >    [17. ],
# >    [15.5],
# >    [15.2],
# >    [16.1]
# > ])

X_train.shape
# > (207, 1)

行数は元の207のまま、列数が1になりました。

2. モデルの準備

今回は回帰モデルを使用します。
冒頭でimportしたLinearRegressionを使ってモデルの定義をします。

# モデルの定義
model = LR()

3. モデルの作成

単回帰モデルを生成します。
モデルの作成とは、データの説明変数と目的変数を用いて、モデルに学習させることです。

model.fit(X_train, y_train)

線形モデルは、モデル作成時に引数として下記のようなオプションを指定することもできます。

指定オプション	概要
fit_intercept	False に設定すると切片を求める計算を含めない。目的変数が原点を必ず通る性質のデータを扱うときに利用。 (デフォルト値: True)
normalize	True に設定すると、説明変数を事前に正規化します。 (デフォルト値: False)
copy_X	メモリ内でデータを複製してから実行するかどうか。 (デフォルト値: True)
n_jobs	計算に使うジョブの数。-1 に設定すると、すべての CPU を使って計算します。 (デフォルト値: 1)

ここで、学習後モデルの傾きや切片を確認してみます。

model.coef_ #傾き
# > array([-2.5023821])

model.intercept_ #切片
# > 134.79948383749922

上記の結果から、今回の線形モデルは
$$ y = -2.5023821x + 134.79948383749922 $$
という数式で表すことができる、ということが分かります。

おさらいですが、この数式でのyは予測する売上数で、
xは温度を示しています。

試しに、このモデルの制度がどれくらいか検証してみましょう。

# 検証（決定係数の計算）
model.score(X_train, y_train)

# > 0.4294602815194137

ちなみに決定係数とは何かと言うと・・・

独立変数（説明変数）が従属変数（被説明変数=目的変数）のどれくらいを説明できるかを表す値である。寄与率と呼ばれることもある。標本値から求めた回帰方程式のあてはまりの良さの尺度として利用される。

と定義されています。
1に近ければ近いほど、説明変数を使って目的変数を表現できていることを表しているようです。

4. 予測

では、実際に売上数を予測してみます。
予測にはpredict関数を使用します。

pred = model.predict(X_test)
print(pred)

# > [ 84.25136537  74.99255159  62.9811175   80.99826864  79.49683938
# >   76.49398085  78.49588653  69.48731097  67.73564349  95.76232304
# >   88.25517673  77.24469548  74.99255159  84.25136537  96.01256125
# >   98.01446693  88.00493852  77.99541011  87.00398568  85.75279463
# >   85.75279463  87.75470031  87.5044621   94.7613702   86.75374747
# >   84.50160358  81.74898327  98.01446693  98.76518156  86.00303284
# >   95.26184662  99.01541977  94.51113199  97.51399051 108.52447176
# >   97.51399051 106.27232787 111.7775685   97.01351409  96.51303767]

ここで、予測に使用したX_testには何が入っていたかというと、
検証用データtest.csvの温度データでしたね。

X_testの中身を確認してみると、最初のデータは20.2となっています。
これを先ほどの数式に当てはめて計算してみると・・・

\begin{align}
y &= -2.5023821 * 20.2 + 134.79948383749922 \\
&= -50.5481184 + 134.79948383749922 \\
&≒ 84.25136
\end{align}

と、確かに計算されていることが分かります。

5. 評価

最後に、signateに提出してモデルを評価するためにCSV出力を行います。

まずは提出用サンプルファイルsample.csvの形状を確認してみます。

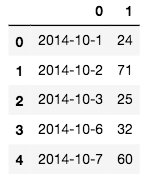
sample.head()

　1列目に日付、2列目に売り上げ数を設定すれば良いことが分かる

予測値をsample[1]を予測した売上数で置き換えCSVファイル出力します。

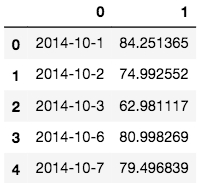
sample[1] = pred
sample.head()

予測した数値が設定されていることが分かります

CSV出力するには`to_csv'関数を使用します。

sample.to_csv('submit1.csv', index=None, header=None)

また、今回はデータの都合上行なっていませんが、このフェーズで検証用データセットに関する
決定係数を確認したりもします。（汎化性能の検証）

# 今回は模擬的に変数を設定しています
model.score(X_test, y_test)

ここで、温度を用いた単回帰分析は終了です。
作成されたCSVファイルですが、この後のカロリーで単回帰分析で作成するCSVと一緒に
signateに提出しようと思います。

単回帰分析（説明変数をカロリーで）

基本的には前半部分と一緒ですが、kcalには欠損値があったため、そこをデータの前処理で補う必要があります。
前半部分と異なる部分だけ補足を入れながら解説します。

1. データの準備（データセットの読み込み）

まずはデータの確認をします。

train.head() #先頭データ
train.describe() #基礎統計量

先頭データ

基礎統計量

記事冒頭でも説明しましたが、kcalには欠損値があります。（画像でいうNaN）
欠損しているデータに関して、今回はkcalの平均値で補い、それを説明変数として使用します。

# kcalの平均値を算出
avg = train['kcal'].mean()

# 学習用データ
# 説明変数に "kcal (カロリー)" を利用
X_train = train['kcal'].fillna(avg)
# 目的変数に "y (売り上げ個数)" を利用
y_train = train['y']

# 検証用（予測用）データ
X_test = test['kcal'].fillna(avg)

データの形状を変換

X_train = X_train.values.reshape(-1,1)
X_test = X_test.values.reshape(-1,1)

2. モデルの準備

# モデルの定義
model2 = LR()

3. モデルの作成

model2.fit(X_train, y_train)

学習後モデルの傾きや切片を確認してみます。

model2.coef_ #傾き
# > array([0.13195178])

model2.intercept_ #切片
# > 33.26061577029441

温度を説明変数としてモデル構築した時とは値が違うことが分かります。

決定係数も確認してみます。

# 検証（決定係数の計算）
model2.score(X_train, y_train)

# > 0.01151900743440537

温度の時と比べ、極端に値が小さいです。

4. 予測

pred2 = model2.predict(X_test)
print(pred2)

# > [88.68036439 88.02060548 86.70108765 86.04132874 89.99988221 88.68036439
# >  90.65964112 86.62318841 87.096943   92.63891786 86.04132874 88.02060548
# >  89.47207508 87.36084656 88.02060548 89.73597865 86.62318841 86.96499122
# >  89.3401233  89.99988221 89.47207508 90.79159291 91.31940004 89.3401233
# >  87.36084656 86.62318841 87.62475013 89.47207508 88.41646082 85.51352161
# >  89.60402686 90.39573756 87.22889478 89.99988221 88.81231617 86.62318841
# >  93.95843568 88.02060548 88.68036439 88.15255726]

5. 評価

CSV出力します

sample[1] = pred2
sample.to_csv('submit2.csv', index=None, header=None)

signateへ提出

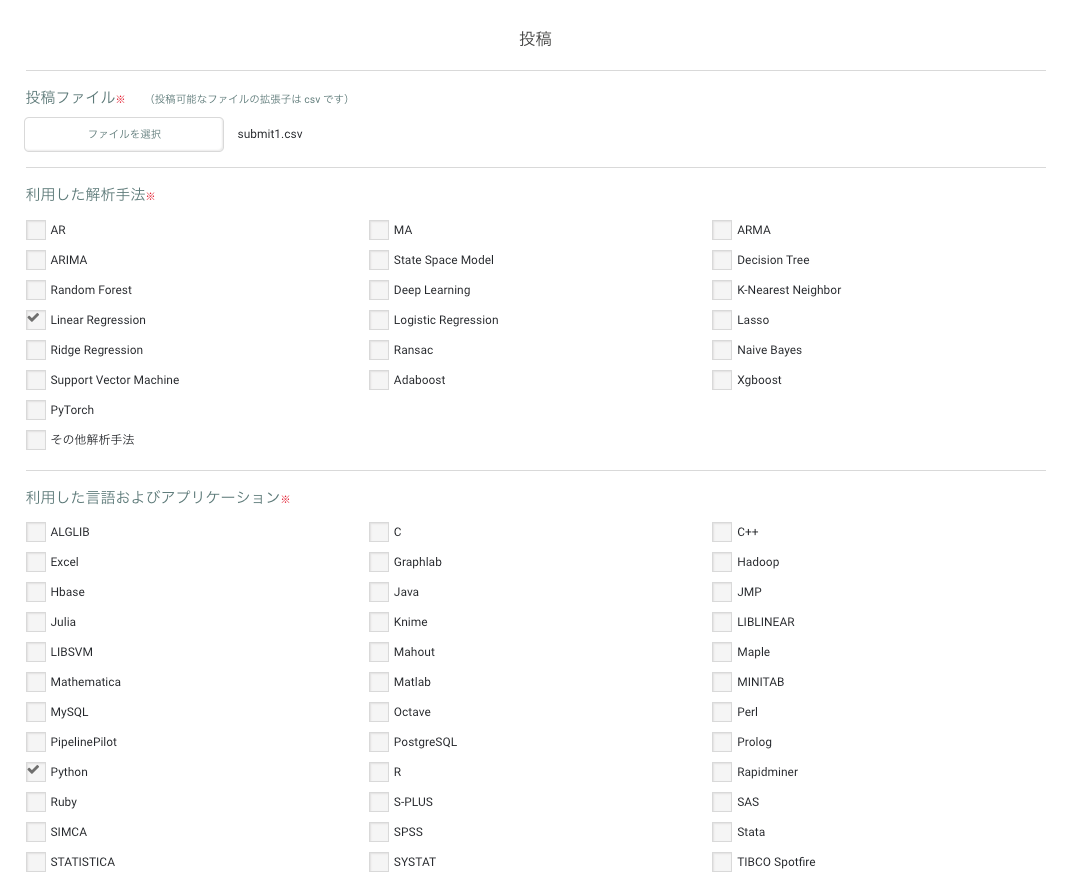
signateのコンペティションページに行き、提出します。

投稿ボタンをクリック

ファイルを選択し、然るべきものにチェックを入れて投稿ボタンを押下します

同じように、submit2ファイルも提出します。

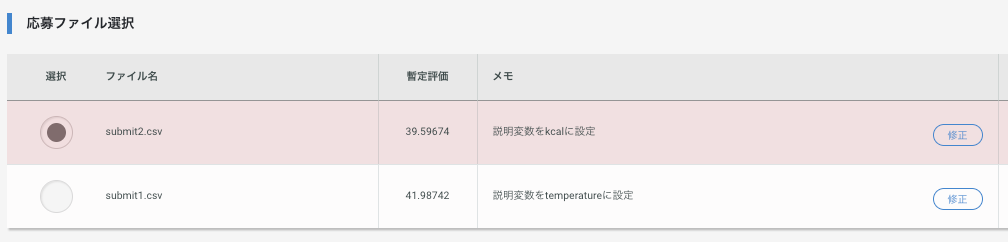
２〜3分経つと、このように評価されると思います。

ここまでで一連の作業が終了です。

お疲れ様でした。

次は重回帰分析を用いて、お弁当の需要予測をしてみたいと思います。