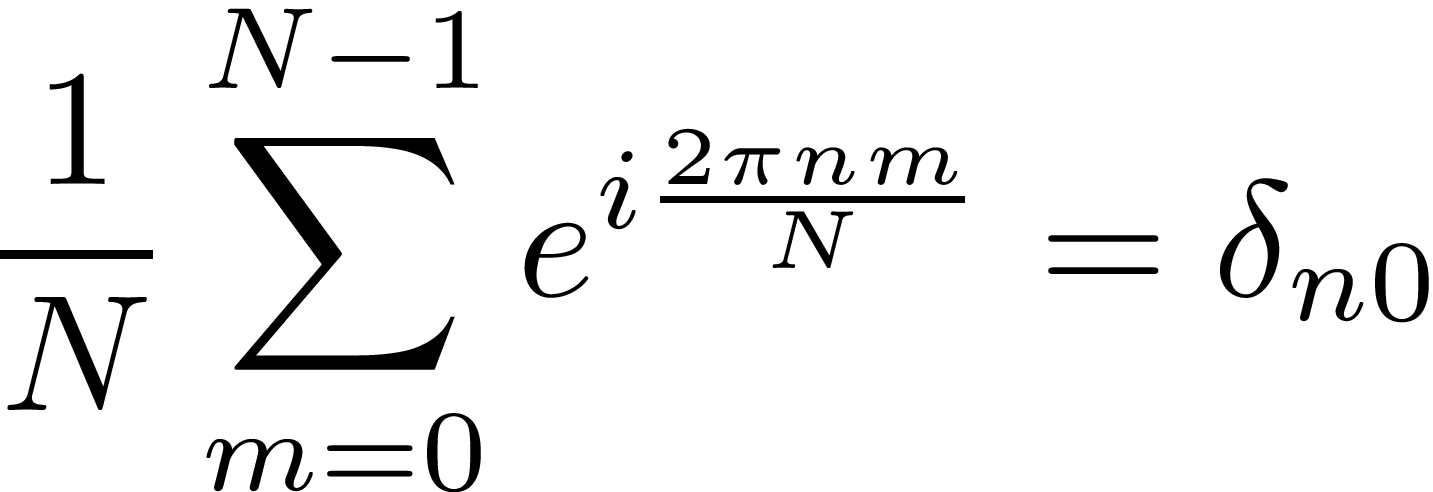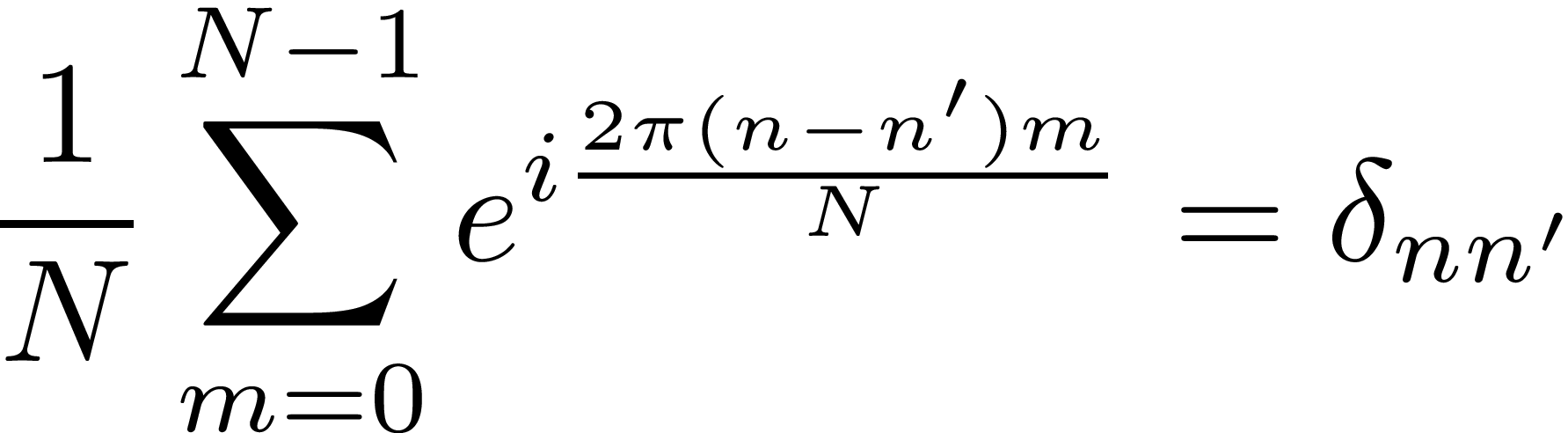実フーリエ級数などを先に勉強するよりも離散フーリエ変換のほうが簡単で役に立つのでこれを先に勉強したほうがいい。やさしいです。オイラーの公式を勉強しておくことー複素数の極座標表示での掛け算、などを知っておく必要がある。https://qiita.com/takaokotani/items/54dd78b20984cdac1f93
オイラーの公式のほうがsin,cosなどより単純でやさしいです。
https://colab.research.google.com/drive/1xpRfu1RkXvgDGXIC8dMJ2p5FyjWeL-r9#scrollTo=xkN0DGEhcruU
大学の先生の多くは三角関数の合成公式(高校生が記憶しているような)は書けないだろう。
まず物理エンジンの動画https://www.youtube.com/watch?v=7hzIhtbxhtM を見ておくこと。これは複素平面における離散フーリエ変換です。円が表すのは$e^{i\omega t}$です。この動画は正確に離散フーリエ変換を表現できています。
離散フーリエ変換の基本になるのは、以下の公式である
Nを整数、nを任意の整数とする。このとき以下がなりたつ。
右辺はクロネッカーのデルタで、n=0のときにのみ1であり、それ以外のnではゼロになることを表す。証明は簡単であるーn=0のときは当たり前だし、ゼロでないときはこの和は等比級数であり
$1+e^{i 2\pi n/N}+e^{i 2\pi n\times 2/N}+e^{i 2\pi n\times 3/N}+...+e^{i 2\pi n\times (N-1)/N}$で等比級数の和の公式からゼロとなることがわかる。書き換えると
となる。これが理解できていればフーリエ変換を理解するのは簡単である。
さらに書き直すと
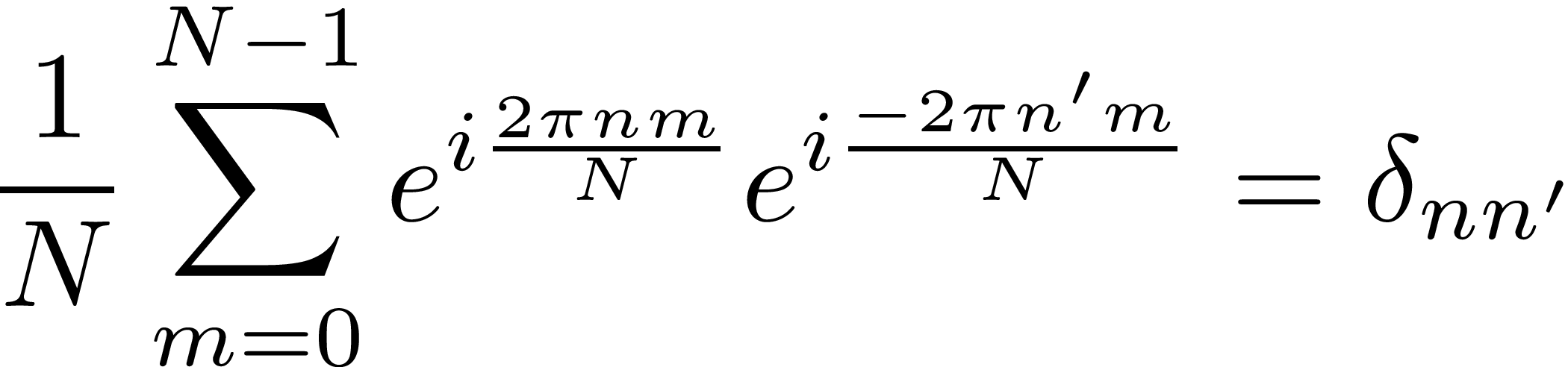
と書けるから、以下のnで指定されるN個のベクトル(nを固定して成分を書くと)
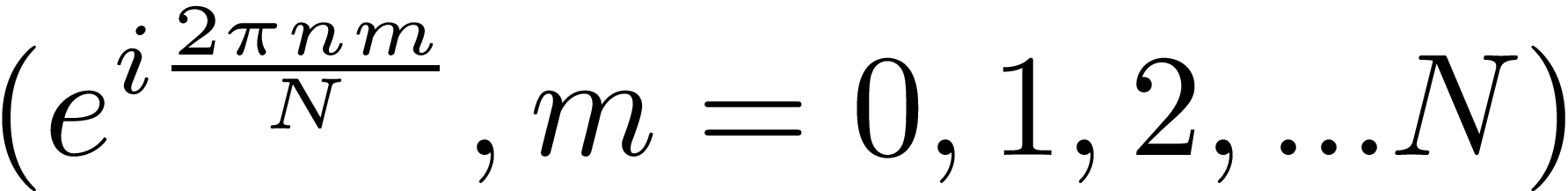
を考えたときに、それらの(複素)内積を考えたときの正規直行性を表していることがわかる。
これを用いれば、
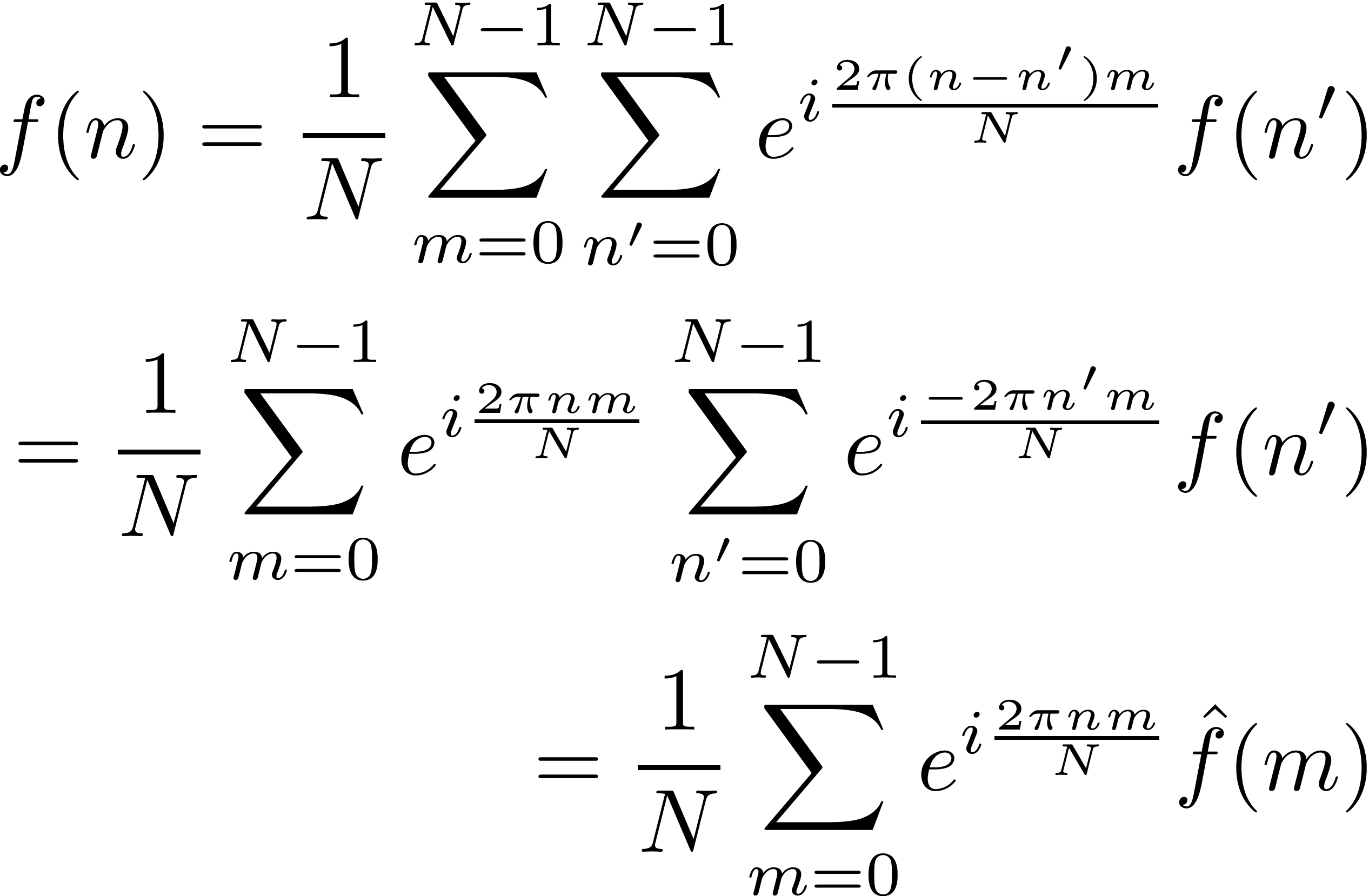
となることがわかる。
ここで
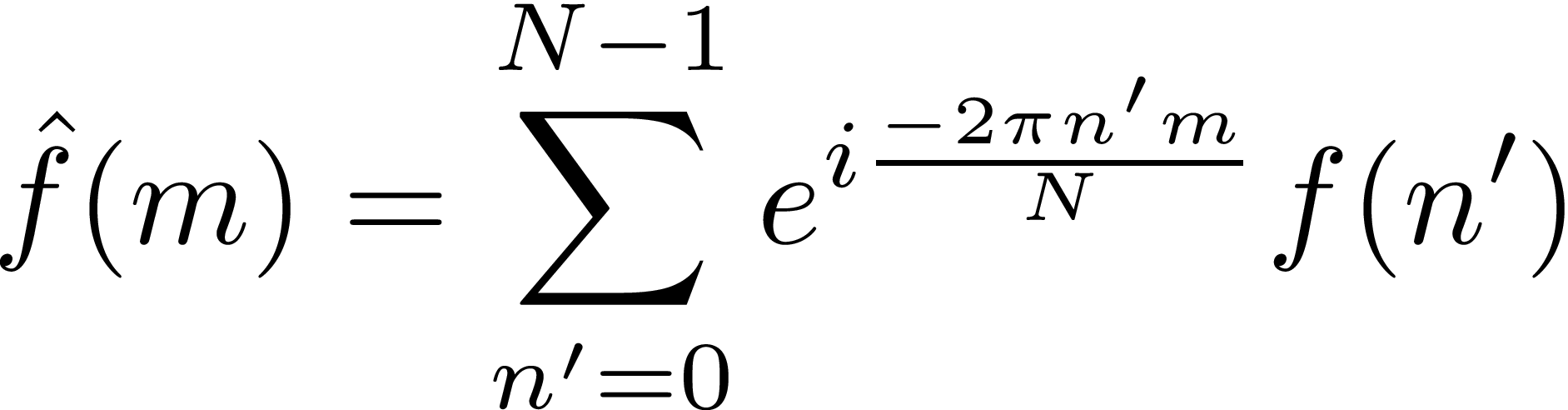
を導入した。これはfをフーリエ変換した量である。フーリエ変換はある特定の基底に対して内積を取る操作である(すなわち成分を抽出するということ)。
あとは連続になるように細かく分割するとかいうような話になるだけ。正規直行性の話は一般的な話で正規直行であれば、どんな関数系をとっても良いという話になる。フーリエ変換、級数の基礎はこれに尽きている。
数式、
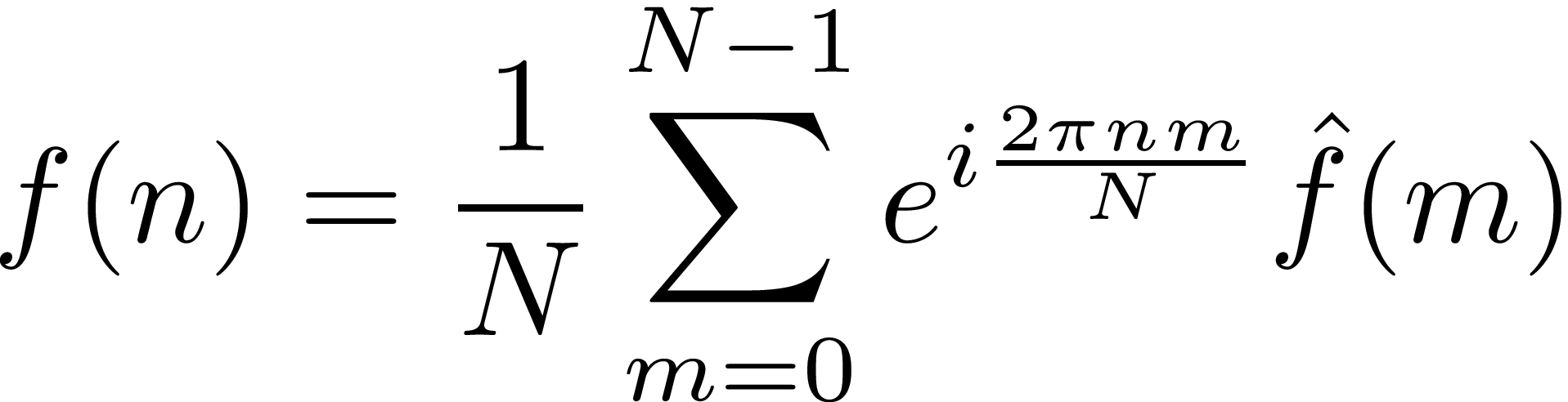
がどうなってるか考えよう。$n$を連続だと思って描画すると物理エンジンの動画になる。$\hat{f}(m)$の位相と振幅が重要です。$N=1$だとどうなるか、$N=2$だとどうなるか...と考えていけばよいです。
大学などで教えるときにはまずオイラーの公式をしっかり使えるようにしてからこのストーリーで教えるのが早いし有効だと思える。
FastFourierTransformation:
https://www.momoyama-usagi.com/entry/math-seigyo14