複素数の理解ー自己チェックリスト #複素数

実数世界は狭すぎる から複素数を理解しておいたほうが得かもしれない。

まず複素数の極座標表示、オイラーの公式を理解すること。複素数が理解できていないと線形代数の理解も限定的になってしまう. 複素数の世界で考えたほうが簡単に理解できることも多い。無理に実数世界に限定して考えようとして余計に難しくなってしまうことがときどきある。
定評のある成書を軸にして、ネット教材なども利用して学ぶのがいいのかも。

チェックは以下の第１段階から。

第１段階：

オイラーの公式とは針が一本の時計(?)である。
$e^{i \omega t}$をアニメ的にイメージせよ。単位円に沿って棒が回転すること。実部や虚部はそれの射影であること. 位置エンコーディングなどの基礎になる。
$e^{i 2 \pi/3}$（そしてそれの複素共役）を複素平面にプロットせよ。複素数の極座標表示。
任意の複素数$x,y,z...$に複素数$e^{i 2 \pi/3}$を乗ずるとどうなるか?を幾何学的に説明せよ。
$\sin(x)$は$e^{ix},e^{-ix}$をもちいてどう書けるか？（これらを引き算すると。。。）.その結果を用い、三角関数の加法定理をオイラーの公式を使って証明せよ。これには$\sin(x+y)$をオイラーの公式で書き直して、指数法則を用いて分解すればよい。
複素数の絶対値が三角不等式$|a+b|\le|a|+|b|$を満たすことを示せ。三角不等式が満たされていないと「中間地点を経由したほうが距離が短くなる」ということがおこってしまう（＝地点の集合が距離空間ではなくなる）。
三角関数のテイラー展開と$e^{i x}$のテイラー展開を比較し、オイラーの公式がなりたつことを確認せよ。テイラー展開の標識を微分してみよ。
$\log(z)$の虚部Im[$\log(z)$]が$z$の位相を与えるとはどういうことか？
代数学の基本定理とは何か（証明はわからなくてもよいけど知っていないといかん）
離散フーリエ変換https://qiita.com/takaokotani/items/bcac5510555e5dc924bc
位置エンコーディングと複素数の関係は？並進対称性とは？

第２段階：複素数まで拡張すると微分方程式は簡単に解ける

$I(t)=S V(t)$であり$V(t)= V_0 e^{-i \omega t}$のときの$I(t)$の振る舞いをアニメ的に説明せよ。ただし、$S,V_0$は複素数である（$S,x_0$は極座標表示で考えること）。応答を支配する$S$は$\omega$の関数であったりするー線形応答関数。$S$が時間によらない場合、$I(t)$と$V(t)$の位相差は固定される。
複素化された微分方程式を理解しておく。以下のニ階微分方程式を$f(t)$が実数関数の場合、複素関数の場合にどうなるかを調べておく。試行解を代入してやれば解ける。ポイントは方程式の実数部分と虚数部分が分離していることーすなわち$f(t)$を複素数の関数だと思って解いたあと、$f(t)$の実数部分だけを取っても（虚数部分だけをとっても）解になっているーこの意味をよく考えることーこれが理解できていなくて前に進めない人もいる。$f(t)$の定義域、値域を実数に限定しておくと難しい方程式が、それを取っ払うことで簡単に解けるようになる。できたらN次線型微分方程式にまで拡張して考えてみる。
$$\frac{d^2 f}{dt^2} + \omega^2 f=0$$
LCRの直列回路を考え共鳴周波数近傍での$S(\omega)$（位相反転）をアニメ的に説明せよ。方程式は、$$L\frac{d^2I}{dt^2} + R\frac{dI}{dt} + \frac{1}{C} I =\frac{d }{dt} V(t)$$である。$V(t)=V_0 \cos(\omega t)$を考えて、応答の遅延について考えよ（位相の遅れ）。$I(t)=S(\omega)V_0 e^{-i \omega t}$の$S(\omega)$を求めよ。原因$V(t)$に対しての応答$I(t)$の位相は必ず遅れる。遅延応答。いろいろな$\omega$の解を重ね合わせて一般の応答が作れる。インパルスに対する応答も作れるが、これには複素積分を使うのが簡単である。
波が$e^{i (kx-\omega t)}$で表されること。実数部分は「本来の波（複素平面での）」の射影であることを理解すること。

第３段階 ：複素解析関数

$f(z)=\sin(|z|)$を$z$で微分せよ。
$f(z)=\sin(z)$は$z$の定義域を複素数全体として値域を複素数とする「複素解析関数」となる。しかし$f(z)=\sin(|z|)$は複素解析関数ではない。どういうことか？（複素数$z=x+iy$を定義域とする関数は$f(x,y)$と書ける、複素解析関数はこれとは違う）。
$f(z)=z^\frac{3}{2}$を$z=0$でテーラー展開せよ。
複素解析関数には極大・極小などが存在しない。極大点、極小点などのかわりに特異点やゼロ点が現れる。
特異点の周りではテーラー展開できない。どういう場合がありえるか？
$f(z)$の微分量$df=\frac{df}{dz}dz$を考える。$dz$は３６０度の向き（位相）が取れるからは$df$はどんな向き（位相）も取れる。同様に$df=f{''} dz^2$はどんな向き（位相）も取れる。$dz$の位相の360度回転に対して$df$は720度回転する。$z$点で解析的ならテーラー展開できるから、$|f(z)|$は極小極大になれない。（二階微分が正だから極値、とならない）。$\frac{df}{dz}=0$の$z$の点でも必ず$|dz|^2$に比例して減っていく方向がある(二階微分がゼロでなければ)。たとえば$f(z)=z^2$は$z=0$で実軸方向にはconvexだが虚軸方向にはconcave.観察してみよう。$f(z)=\sqrt{z}$なども考えてみよう。
代数学の基本定理(多項式が完全に因数分解できること）：微分的に大雑把に考える。複素解析関数$f(z)$が$z$でテイラー展開できるとすると$z$を少し動かして$|f(z)|$が必ず小さくなるようにできる（$|f(z+dz)|<|f(z)|$となるように$dz$を選べる)。だいたいは上の問題のイメージ。すこしずつ$z$を動かすことを考えると、ある閉集合で定義された特異点をもたない複素解析関数$f(z)$は$|f(z)|$の最小値、最大値を閉集合の境界線上で持つことになる。あるいは閉集合の内部のゼロ点が最小値になりうる。N次の多項式（$z^N$の係数は１とする）を考えるなら、最悪の場合でも$|dz|^N$で減っていくような方向が選べる。多項式では大きな領域をとればその境界は非常に大きな値であるので、内部にゼロ点を必ず持つことになる。ゼロ点をもてばそのような因子で多項式を割ることができることになる。(https://kaityo256.github.io/python_zero/basic/index.html ニュートン法の収束地図も参考になる）.
特異点がなければ周回積分がゼロになるのは複素解析関数の意味を考えるとほとんど当たり前の話。
役に立つ複素積分はそんなにたくさんあるわけでもない。一つはステップ関数のフーリエ変換である。

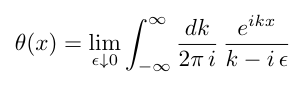
https://sci-tech.ksc.kwansei.ac.jp/~okamura/anonymous/lecture/MathPhys/report/MP2-19rep2.pdf
線形応答や制御理論などは、この積分がわかっていないと困難である。

第４段階：実数を行列化するとエルミート行列、$e^{i \theta}$を行列化するとユニタリ行列。

複素ベクトルの内積が三角不等式を示すことを示す。もし複素共役を取らないと三角不等式が成り立たないことを示す。
実数の概念を行列化するとエルミート行列になるとはどういうことか？
$H$を行列として$e^{iHt}$というものを考える。どう考える？それの満たす微分方程式は？
可換群の既役表現は一次元

つづく。。。

数学予備：

コーシー列が必ず収束するのが閉集合（完備な集合）。
距離空間と三角不等式。
積分とは細かく分けて足すことである、測度。
確率とは総和＝１を分割する話である。