リモートワークライフのための科学的ダイエット：酢がダイエットに良いという論文を見つけたので自分の体でPoC(検証)した件

このエントリは一体何か

ABEJAのデータサイエンティスト/エンジニアの高橋です。
みなさん、リモートワークしてますか？
私はかれこれ半年ほどリモートワークをしています（時々オフィスに行きます）
さて、みなさん、運動量は足りてますか？？
わき腹を指でつまんでみてください・・・
体重が線形に単調増加曲線を描く現実に心がチクリと痛んだ人はいませんか？
私もつい数カ月前はそうでした。

しかし、ある論文と巡り合ったことで転機が訪れたのです・・・

今回は、リモートワークライフを送る全ての職種の皆さまにささげるエントリです。
酢がダイエットに良いという論文を見つけたので、**自分の体でPoC(仮説検証）**をしたことを報告したいと思います！

全てはこの論文との出会いから始まった

ライフハックに有益な一次情報を求め、論文ＰＤＦをさまよっていたある日、私はこの論文に出会ったのでした。

論文ＰＤＦ : https://www.jstage.jst.go.jp/article/jsnfs/67/4/67_171/_pdf

論文の概要

ざっくり言うと次の通りです。

• ラットを使って酢が体脂肪に及ぼす影響を調べた
• その結果、有意に体脂肪の減少が見られた
• ミツカンの協力の元行われた実験でも、酢を飲んだ被験者は有意な体脂肪減少が確認された

結論は分かりました。
次に知りたいのは、その基本的なメカニズムです。
なぜ酢を飲むと、体脂肪が減りやすくなるのか？
では、もう一段階論文の内容を掘り下げて見て行きましょう。

鍵を握るのはAMPKという酵素

マウスの体内及び人体内で体脂肪の減少の鍵を握っていると考えられるキーファクターがあります。
それがAMPK(アデノシン一リン酸活性化プロテインキナーゼ）という酵素です。

• Wikipedia:ＡＭＰＫ（＝AMP活性化プロテインキナーゼ）

体脂肪の減少に関連すると見られる性質をWikipediaのエントリから抜粋してご紹介します。

・・・細胞のエネルギー状態の恒常性に関係する酵素で、細胞のエネルギーが低下しているときにグルコースと脂肪酸の取り込みと酸化を活性化する

脂肪酸の取り込みと酸化を促す＝体脂肪の燃焼を促すと解釈して良いかと思われます。

・・・脂肪酸、コレステロール、トリグリセリドの合成が阻害され、脂肪酸の取り込みとβ酸化が活性化される

脂肪酸、トリグリセドの合成が阻害される＝体脂肪の蓄積が阻害されるという解釈で良いかと思います。

脂肪酸のβ酸化＝脂肪燃焼反応のことを表しています。

抜粋で紹介しましたが、ＡＭＰＫには体脂肪減少に効果がありそうな機能を持っていることが伺えます。

**酢を飲むとＡＭＰＫが活性化される**ということがマウスの実験で確認されたというのが、今回紹介する論文の中で最も重要な知見だと私は見ています（特にダイエットの観点から！）

実験結果の抜粋紹介

基本的なメカニズムをザックリと抑えたところで（詳細な生化学反応経路の話は、本エントリの方針として割愛させていただきます）、肝心の実験結果に関する記述を抜粋してご紹介します。

酢酸を与えたラットと、そうではないラットを比較したところ・・・

• 体重増加が抑えられていた。
• 同じ量の食事を摂取しても体重が増えにくかった。
• 体内の体脂肪の蓄積量が減っていた。

ということがラットの実験で確認されたとあります。

また、2009年のミツカンとの協力で行われた人体における実験結果を引用しており、

• サンプル数は175名
  • 25～60歳の健康な人
• リンゴ酢を含んだ飲料を朝夕に摂取し、これを12週間（約3カ月）続けたところ、
• 体重、ＢＭＩ、内臓脂肪、ウェスト、血中中性脂肪レベルがいずれも改善した

という実験結果を紹介しています。

ミツカンの実験結果

ミツカンの実験の一次資料は無いかと思い、調べたところ無事に発見することが出来ました。

• ミツカン：お酢の継続摂取で内臓脂肪が有意に低下！メタボリックシンドロームの予防に期待

実験結果の部分を抜粋してご紹介します。

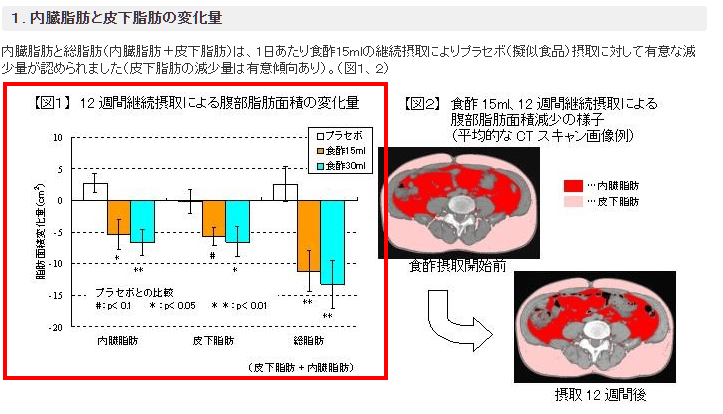
腹部の体脂肪の変化

プラセボ群（酢を摂取していない）と比べて、酢を摂取した群では体脂肪が減っていることがグラフから確認できます。

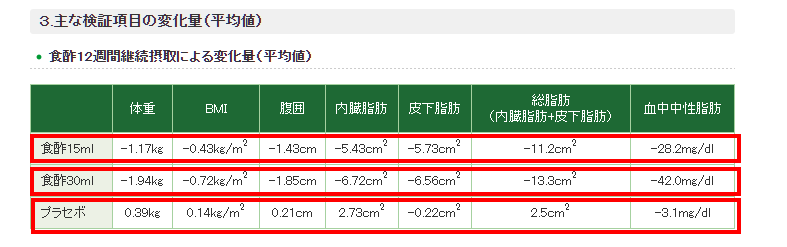
実験結果サマリ

体重、ＢＭＩ、ウェスト、内臓脂肪、皮下脂肪、血中脂肪の変化を比較したものですが、酢を摂取するほど体脂肪減少に効果が表れている傾向が確認できます。

こうして、仮説を立てるのに必要な材料は揃ったということで、私は自分の体での仮説検証(PoC)に取り組むことにしたわけです。

仮説検証(PoC)

仮説

「酢の摂取を継続すると、体脂肪は減少する」と仮定します。

検証方法

以下のようにして今回の仮説を検証します。

• 黒酢を水で割ったもの(黒酢15-20ml + 水500cc)を摂取し続ける。
  • どうせ飲むなら好きな酢を飲みたい（ほのかなうま味があるので黒酢が好き）
  • 毎日平均で黒酢を100ml前後摂取（結構ガブガブ飲んでいた模様）
• 測定期間は8月下旬～12月2日（約3カ月）
  • ミツカンの実験期間とほぼ同じ
  • 黒酢ドリンクの摂取開始は９月に入ってから
    • 9/1～9/5は体重測定を忘れていた...
• 体重の変化を記録してプロットし、近似曲線を求めて体重減少量を推定する
  • 一日で複数回記録することが多いので、散布図でプロットして近似曲線を求める
  • ２次＆３次近似

検証

検証にあたり、記録した体重の推移をJupyterNotebookで分析しました。
体重の推移は diet_history_2020.tsv にＴＳＶ形式で記録しました。
ファイルのカラムは次の通りです。

• date : 体重を記録した日付
• body_weight : 体重(kg)

使用するモジュール群の読み込み

今回使用するモジュール群を読み込みます。

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib as mpl
import matplotlib.pyplot as plt

# 近似関数の決定係数(R2)計算用
import sklearn.metrics as metrics

from datetime import timedelta

記録した体重の推移を読み込む

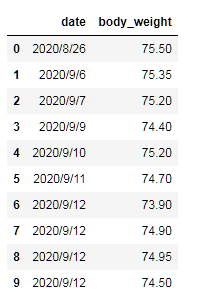
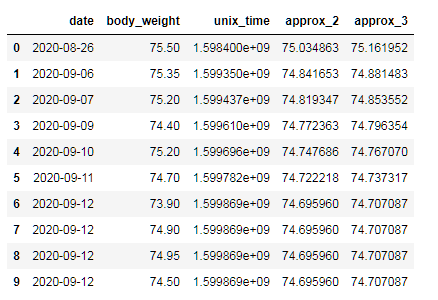
df_diet = pd.read_csv('./diet_history_2020.tsv', sep='\t')
df_diet.head(10)

このように記録されています。

前処理

日付文字列(YYYY-mm-dd)をタイムスタンプ型に変換した後、近似曲線を推定時に使う座標値としてunix_timeをカラムに追加します。

• x座標値がタイムスタンプ型だと近似曲線の推定時にエラーが起きるためです。

df_diet['date'] = pd.to_datetime(df_diet['date'])

# 近似曲線推定時に使う
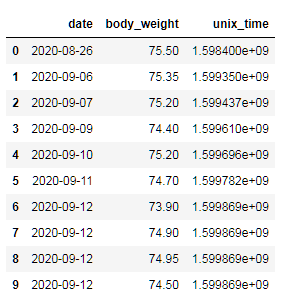
df_diet['unix_time'] = df_diet['date'].apply(lambda x:x.timestamp())

df_diet.head(10)

近似曲線の推定

np.polyfit を使って、近似曲線を推定します。

fn_aprox2 = np.polyfit(df_diet['unix_time'], df_diet['body_weight'], 2)
fn_aprox3 = np.polyfit(df_diet['unix_time'], df_diet['body_weight'], 3)

df_diet['approx_2'] = np.poly1d(fn_aprox2)(df_diet['unix_time']) #二次近似曲線
df_diet['approx_3'] = np.poly1d(fn_aprox3)(df_diet['unix_time']) #三次近似曲線

df_diet.head(10)

approx_2 に二次近似曲線の値が、approx_3 に三次近似曲線の値が入っています。

体重の推移と近似曲線をプロットする

• metrics.r2_score を使い、各近似曲線の決定係数($R^2$値)を求めます。
• x軸の表示範囲のマージンを timedelta(days=14)を使って調節します。

figure = plt.figure(figsize=(16,8))
mpl.rcParams['font.family'] = 'IPAexGothic'

# 近似曲線の決定係数を求める

# 二次近似曲線の決定係数
r2_2 = metrics.r2_score(df_diet['body_weight'], df_diet['approx_2'])
info_r2_2 = '$R^2={:.03}$'.format(r2_2)

# 三次近似曲線の決定係数
r2_3 = metrics.r2_score(df_diet['body_weight'], df_diet['approx_3'])
info_r2_3 = '$R^2={:.03}$'.format(r2_3)


# invalid type promotion 対策
plt.scatter(df_diet['date'].values, df_diet['body_weight'], label=u'体重(記録)')

plt.plot(df_diet['date'], df_diet['approx_2'], label=u'近似曲線(2次, {})'.format(info_r2_2))
plt.plot(df_diet['date'], df_diet['approx_3'], label=u'近似曲線(3次, {})'.format(info_r2_3))

# x軸の表示期間のマージン調整（見やすくする）
time_margin = timedelta(days=14)
plt.xlim(df_diet['date'].min() - time_margin, df_diet['date'].max() + time_margin)
plt.xlabel(u'日付', fontsize=16)
plt.ylabel(u'体重(kg)', fontsize=16)
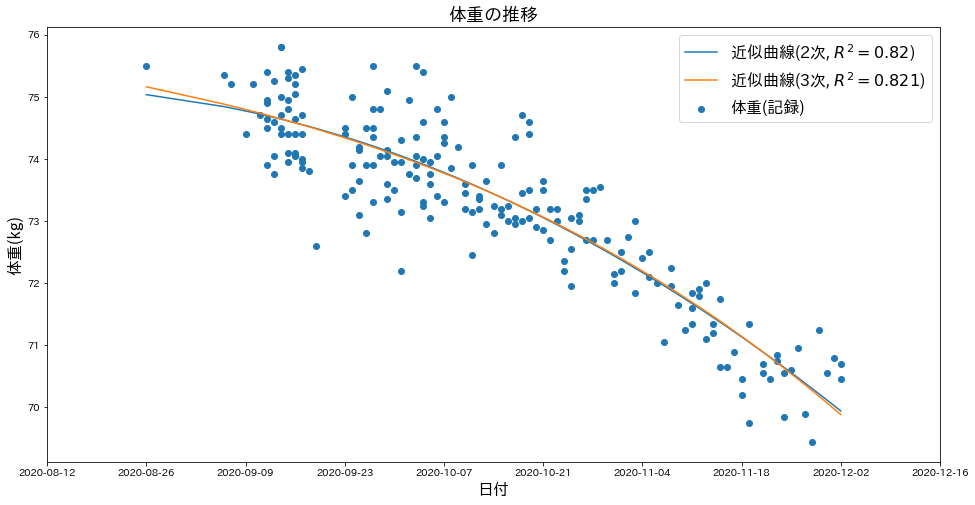
plt.title('体重の推移', fontsize=18)
plt.legend(fontsize=16)
plt.show()

体重の推移をプロットすると、ちゃんと体重が減少していることが確認できました。
こうしてプロットして視覚化すると実感が違いますね。

体重減少量を推定する

さて、具体的にはどれくらい体重が減ったのでしょうか？
近似曲線を使って推定したいと思います。

• 二次＆三次近似曲線を使い、黒酢ドリンク摂取開始前と測定期間終了時点の推定体重を得る
• 推定体重の差分を求め、体重減少量と仮定する

first_rec = df_diet.iloc[0]
last_rec = df_diet.iloc[-1]
start_weight = np.mean(first_rec[['approx_2','approx_3']])
end_weight = np.mean(last_rec[['approx_2', 'approx_3']])
diff_weight = start_weight - end_weight
print('黒酢ドリンク摂取開始前 : {:.04}kg'.format(start_weight))
print('測定期間最終日         : {:.04}kg'.format(end_weight))
print('体重減少量(推定)     : {:.03}kg'.format(diff_weight))

出ました！

• 黒酢ドリンク摂取開始前 75.10kg
• 測定期間最終日 69.10kg

体重減少量はなんと 5.18kg！！

ミツカンの実験結果と比較したいと思います

（再掲）：

簡単な考察

• 酢を毎日 30ml 摂取した集団では、12週間(約３カ月）で1.94kgの体重減少
  • 酢を毎日15ml摂取し集団と比べて体重の減少量は 0.77kg 多い
• 黒酢を毎日約 100ml 前後摂取していたので、
  • $ 15ml + 15ml \times 5.667 = 100ml$
  • 単純計算で導かれる体重減少量は
    • $ 1.17 + 0.77 \times 5.667 = 5.5333 (kg) $

体重測定から導かれた体重減少量（推定）は、5.18kg なので、誤差 0.35kg。
ミツカンの実験から導いた推定と近い値が得られました。

なお、このダイエット期間中ですが、筋トレの際の負荷を減らすことなく過ごせました。
恐らく筋肉は溶けていないのではないかと期待しています（楽観）。
それどころか、筋トレの負荷をじわじわ上げる事が出来ているので、筋肉量は増えている？

と言うことを踏まえると、体重減少の内訳はほぼ体脂肪であると推定されます。

酢のダイエット効果、すごい！！

Next Step

今後取り組みたい課題としては...

• 黒酢ドリンクダイエットを継続し、更なるサンプル数を集める
  • 自分の努力で十分実現可能
• 再現実験結果が得られたら、考察・検証する
  • 現状ではサンプル数＝１（私自身）
• メタアナリシス的な分析
  • 同様の実験や、ダイエット記録の公開状況に依存

外部環境に左右される課題が多いですね（汗
まずはこのダイエットを継続し、体重の記録を続けて参りたいと思います。
（あと5kg体脂肪減らしたら、シックスパックいけるかな？）

まとめ

データサイエンスというよりは、バイオサイエンス＆ボディハック寄りの内容でお届けしましたが、自分の体でちゃんと効果を検証出来たのは嬉しかったです。

限度はあるでしょうが、酢を頻繁に摂取すると、ダイエット効果も摂取量に比例して高まる可能性が示唆されました（ただし、サンプル数＝１ですが・・・）

このエントリをご覧になられた方におかれましては、もし興味を持って頂けたら嬉しいです。
更に再現実験をして結果を共有してもらえたら、飛び上がって喜びます。臨時アドベントカレンダーでご紹介します！（体質に合わない場合は、御無理はなさらぬように・・・）

現場からは以上です！

ということで、体調にお気をつけいただきながら、良い年末年始をお過ごしください！

お知らせ：ABEJA awaits your joining!

現在ＡＢＥＪＡでは一緒にＡＩの社会実装を進める仲間を募集しています！
世の中をアップデートする最前線の現場に、あなたも飛び込んでみませんか？
どんな人がＡＢＥＪＡで働いているのか知りたくありませんか？
まずは気軽にカジュアルインタビューから始めませんか？
【募集職種一覧はこちら！】