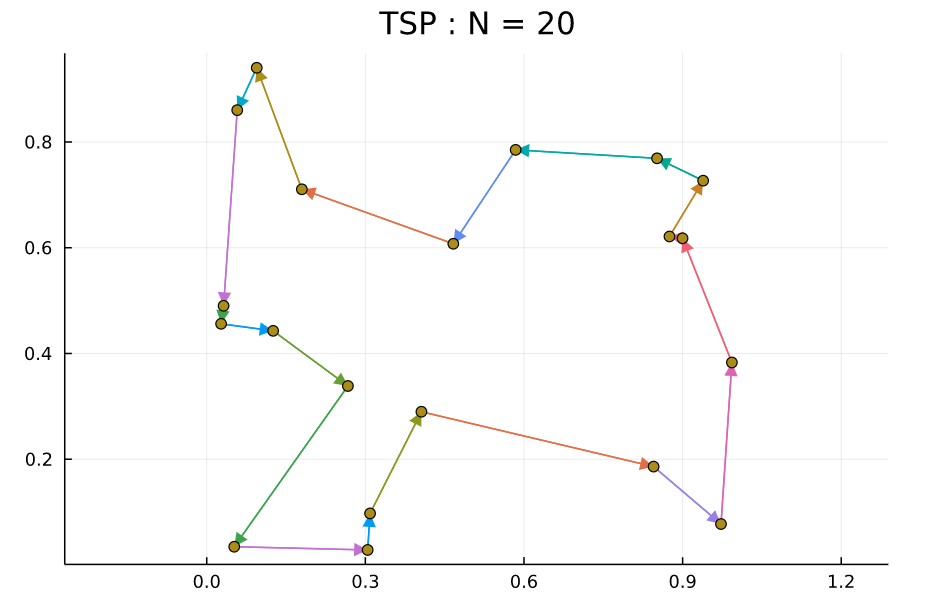
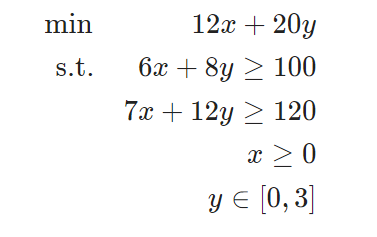巡回セールスマン問題 (traveeling salesman problem; TSP)
はじめに
巡回セールスマン問題はいくつかの地点を必ず1回だけ通るときの最短経路を求める問題です。すべての経路を計算すると計算量は O(n!) となります。なので特に工夫せずに解こうとすると、nが20くらいまではまだ計算可能ですが30とかになると途端に厳しくなります。
全ての頂点をちょうど1回ずつ通って出発点に帰ってこれるようなグラフをハミルトングラフ(ハミルトン閉路)といいます。
TSPの最先端
TSPの最先端は知りたい方はTraveling Salesman Problemをご覧ください。13億の地点を周遊する様子や、TSPの歴史を見ることができます。
またこのサイトでは、すでに出来上がっているTSPの解法をダウンロードできるので、使ってみたい方はライセンスをよく確認したうえで使ってみてください。youtubeに実際にダウンロードして動かしている方の動画があるので是非そちらもご覧になってみてはいかがでしょうか。Nが2000くらいでもかなりのスピードで解いているのがわかります。
近似解とメタヒューリスティクス
今回は近似手法やメタヒューリスティクスは使わずに少ないNに対して厳密解を求めることをします。ですので、私が参考にした動画を紹介してこの章を終わろうと思います
近似手法としては近似率2の「Double tree アルゴリズム」、近似率1.5の「Christofiedesのアルゴリズム」などがあります。詳しくは離散数学入門#7: ハミルトングラフと巡回セールスマン問題 がわかりやすいです。
メタヒューリスティクスは近傍という概念を使って最適解を探し続けます。詳しい説明はこちらメタヒューリスティクス(代表的な手法)が詳しいです。
動画にもある通り近似手法とメタヒューリスティクスの違いは理論的な保証を持つかどうかの違いであるとのことです。
巡回セールスマン問題の定式化
巡回セールスマン問題の定式化から始めます。以下「しっかり学ぶ数理最適化」の巡回セールスマン問題の定式化です。
\begin{align}
minimize &\quad \Sigma_{u \in V} \Sigma_{v \in V, u \not = v} d_{uv}x_{uv} \\
s.t &\quad \Sigma_{v \in V, u \not = v} x_{uv} = 1, \quad v \in V, \\
&\quad \Sigma_{v \in V, u \not = v} x_{vu} = 1, \quad v \in V, \\
&\quad \Sigma_{(u,v) \in E(S)} x_{uv} \leq |S| - 1, \quad S \subset V, |S| > 2, \\
&\quad x_{uv} \in (0, 1)
\end{align}
文字の説明から行います。$V$ は都市の集合です。$d_{uv}$ は2都市$u,v$ の距離を表しています。$x_{uv}$ は変数で、都市 $u$ から都市 $v$ を訪問するとき1をとり、それ以外は0を取ります。$E(s)$ は両端点 $u,v$ がともに頂点集合 $S$ に含まれる辺 $(u,v)$ の集合です。
次に制約条件の説明です。1番目と2番目の条件はある都市に必ず1回は訪れるという制約です。3番目の制約は__部分巡回路除去制約(subtour elimination inequality)__ といって部分巡回路を持たないという制約です。
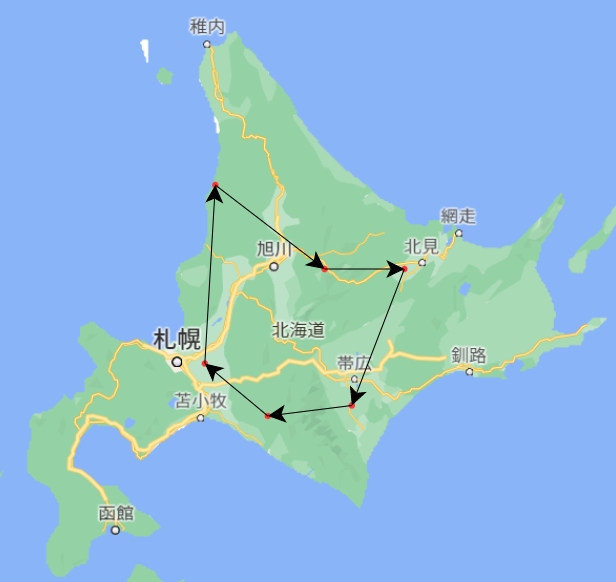
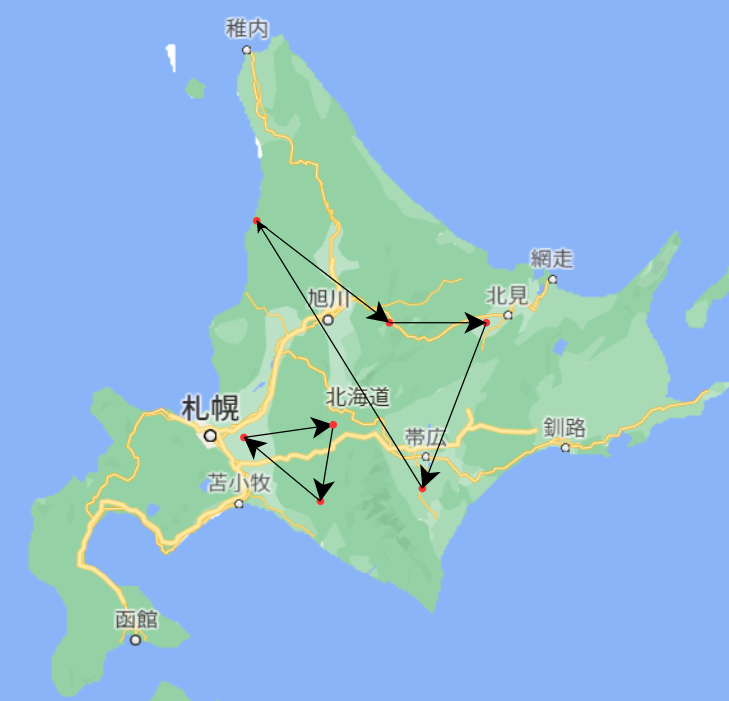
つまり、こういう感じで閉路が二つできるようなものはダメですという制約です。
ここで少し問題なのは、この定式化で素直に解こうとすると制約式の数が $2^{|V|} - |V| - 2$ と多すぎるということです。そのため求解には制約条件を逐次的に追加する切除平面法といわれる別な手法が必要になります。
ただ、今回は補助変数を導入することで制約式の数を $(|V| - 1)(|V| - 2)$ にできるような制約を掛ける方法で進めていきたいと思います。
MTZ制約 ( Miller - Tucker - Zemlin constraint )
先に制約の具体的な式を見ていきます。
\begin{align}
&\quad y_u - y_v + |V| x_{uv} \leq |V| - 1, \quad u,v \in V, u \not = v, \\
&\quad y_s = 0, \\
&\quad 1 \leq y_v \leq |V| - 1, \quad v \in V \setminus (s)
\end{align}
この制約式は何をしているかというと、まず $y_s$ というスタート地点を決めます。その後、次の頂点に移動するときスタート地点からいくつの辺を通ったてきたかを記録するのが $y_v$ です。
これを使うとなぜ部分巡回路が除去できるかは具体的な例を考えればわかります。
まず、$x_{uv} = 0$ の場合、右辺は|V| - 1と十分に大きいので不等式は必ず満たされます($y_vは高々|V| - 1$である)。
次に、$x_{uv} = 1$ の場合、不等式は $y_u \leq y_v - 1$ です。ここで、ある頂点集合のうち、頂点を三つ選び且つそれが閉路になっているようなグラフを考えます。この時不等式は次のようになります。
\begin{align}
y_1 &\leq y_2 - 1 \\
y_2 &\leq y_3 - 1 \\
y_3 &\leq y_1 - 1 \\
\end{align}
ただ、これを満たすような$y_1, y_2, y_3$ は存在しません。つまりこの制約式は閉路を許さないのです。このような制約をMTZ制約といいます。これを先ほどの定式化部分に置き換えると
\begin{align}
minimize &\quad \Sigma_{u \in V} \Sigma_{v \in V, u \not = v} d_{uv}x_{uv} \\
s.t &\quad \Sigma_{v \in V, u \not = v} x_{uv} = 1, \quad v \in V, \\
&\quad \Sigma_{v \in V, u \not = v} x_{vu} = 1, \quad v \in V, \\
&\quad y_u - y_v + |V| x_{uv} \leq |V| - 1, \quad u,v \in V \setminus (s), u \not = v, \\
&\quad y_s = 0, \\
&\quad 1 \leq y_v \leq |V| - 1, \quad v \in V \setminus (s) \\
&\quad x_{uv} \in (0, 1)
\end{align}
となります。ここで、$y_u - y_v + |V| x_{uv} \leq |V| - 1, \quad u,v \in V, u \not = v$ 部分が $y_u - y_v + |V| x_{uv} \leq |V| - 1, \quad u,v \in V \setminus (s), u \not = v$ となっていることに注意しましょう。これは頂点 $s$ を含まない閉路は許しませんという意味です。逆に頂点 $s$ を含む閉路ならokということです。
あとはJuMP.jlというJuliaの最適化パッケージでこの式を表現し解くだけです。
JuMP.jlについて
詳しくは公式ドキュメントを見ていただくといいと思います。ドキュメント読むの苦手人間な私ですが、Juliaはドキュメントがかなり見やすいのでいったんドキュメントを見ていただくのがいいかもしれません。
さてJuMP.jlを一言でいうならモデリング言語といったイメージでしょうか。ソルバーをインストールしそれぞれのソルバーの違いを意識せずにモデルが記述できます。ソルバーは商用のものもあれば、すべてJuliaで書き直されていて無償ものもあります。今回使用するのも無償のソルバーを使っています。
ここでちょっとした注意ですが、公式ドキュメントにも書いてある通りJuMPはバージョンの互換性の関係から、別プロジェクトを立ち上げてバージョン管理を行うことが推奨されています。
# パッケージ管理モード
> generate MyProject
> activate .
# あとは好きなようにパッケージをインストールしよう!
では簡単にJuMPの使い方を紹介したいと思います。(JuMP.jlのチュートリアルから抜粋)
using JuMP
using GLPK
model = Model(GLPK.Optimizer)
@variable(model, x >= 0)
@variable(model, 0 <= y <= 3)
@objective(model, Min, 12x + 20y)
@constraint(model, c1, 6x + 8y >= 100)
@constraint(model, c2, 7x + 12y >= 120)
print(model)
optimize!(model)
@show solution_summary(model)
model = Model(GLPK.Optimizer)
まずはソルバーを選択します。このモデルに変数を定義したり制約を定義したりします。
@variable(model, x >= 0)
@constraint(model, c1, 6x + 8y >= 100)
変数はと制約はマクロを使って定義します。基本の書き方は上記のような形ですが、次のような書き方も可能です。
@constraints(model, begin
2x <= 1
x >= -1
end)
ほかにも
@constraint(model, sum(z[i] for i in 1:10) <= 1)
$z_1 + z_2 + ... + z_{10} \leq 1$ といったような書き方もできます。
optimize!(model)
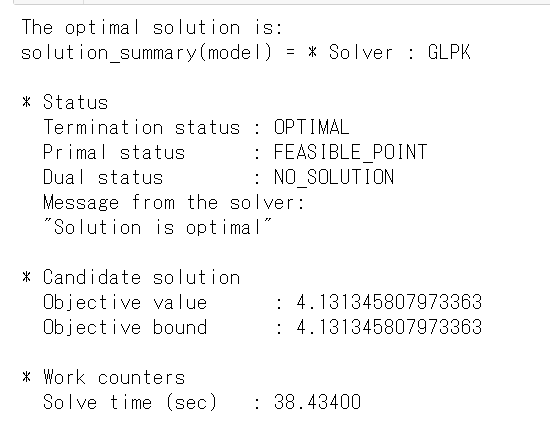
最適化を行うのはこれだけです。モデルの要約は
solution_summary(model)
を見たりprintln(model) をみたりするといいと思います。
コード
メイン関数
using JuMP
using GLPK
using Plots
using Random
using LinearAlgebra
# 都市生成
N = 20
X = rand( MersenneTwister(20211108), N, 2 )
# TSPを解く
res = traveling_salseman(X)
# 結果のプロット
plot_res(res)
モデル
function traveling_salseman(X)
N = size(X)[1]
# 各頂点の距離を計算
dist = zeros(N,N)
for i in 1:N
for j in i+1:N
dist[i,j] = sqrt( sum( ( X[j,:] .- X[i,:] ).^2 ) )
end
end
dist = Symmetric(dist)
#= モデル定義 =#
model = Model( GLPK.Optimizer )
#= 変数定義 =#
@variable( model, x[1:N,1:N], binary = true )
# 各頂点を訪問する補助変数
# HACK: y_1 = 0 の表し方がわからない
@variable( model, 1. <= y[2:N] <= N - 1. )
#= コスト関数 =#
@objective(
model,
Min,
sum(
dist[i,j] * x[i,j] for i=1:N,
j=1:N
)
)
#= 制約条件 =#
# 各都市に入る辺と出る辺はちょうど一本ずつ
@constraints(
model,
begin
[ i in 1:N ], sum( x[i,:] ) - x[i,i] == 1
[ j in 1:N ], sum( x[:,j] ) - x[j,j] == 1
end
)
# 部分純回路除去不等式
# MTZ制約
for i in 2:N
for j in 2:N
if i != j
@constraint(
model,
y[i] - y[j] + N * x[i,j] <= N - 1
)
end
end
end
optimize!(model)
Test.@test termination_status(model) == MOI.OPTIMAL
Test.@test primal_status(model) == MOI.FEASIBLE_POINT
println("The optimal solution is:")
#println(model)
@show solution_summary(model)
return value.(x)
end
結果のプロット
function plot_res(res)
N = size(X)[1]
p = plot(legend=false, aspect_ratio=1)
for i in 1:N
k = findall( x->x==1.0, res[:,i] )
plot!(
p,
[X[i,1]; X[k,1]],
[X[i,2]; X[k,2]],
arrow=(:closed, 3.0)
)
end
plot(p, title="TSP : N = $N")
scatter!(X[:,1], X[:,2], legend=false)
end