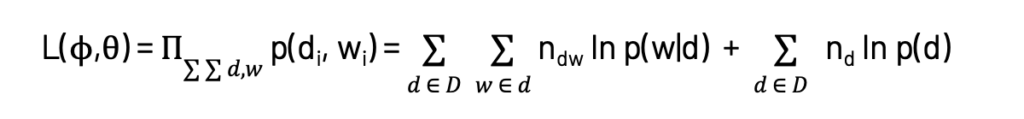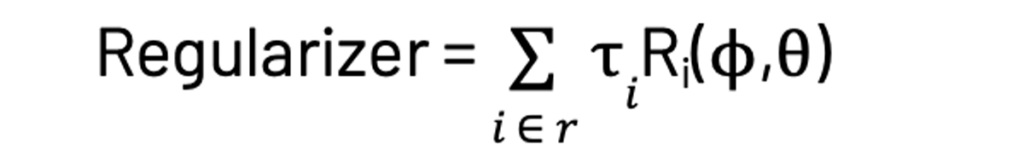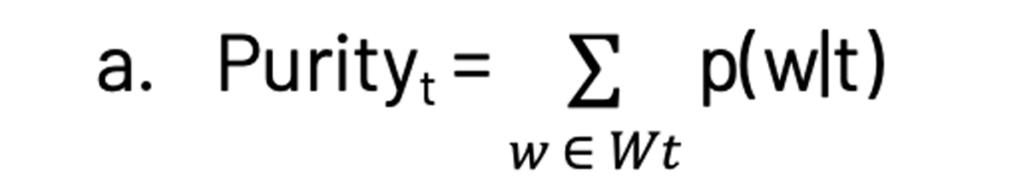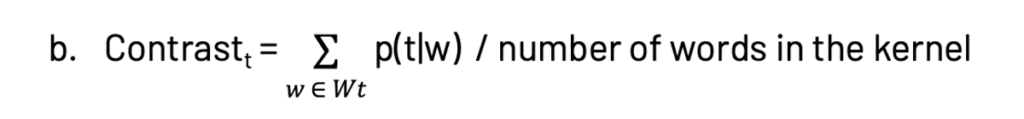Topic Modeling for Text with BigARTM -の翻訳です。
本書は抄訳であり内容の正確性を保証するものではありません。正確な内容に関しては原文を参照ください。
この記事はテキスト分析におけるトピックモデリングの記事の続編となります。以前、我々はPySparkのMLlibで利用できるLDA(Latent Dirichlet Allocation)トピックモデリングライブラリを見ていきました。LDAは非常に能力のあるツールですが、ここではBigARTMと呼ばれるよりスケーラブルかつ最先端の技術を見ていきます。LDAはトピックと単語の分布に対してDirichlet分布を仮定する2レベルのベイジアン生成モデルに基づいているものです。BigARTM(BigARTM GitHub、https://bigartm.org)は、トピック推論問題をシンプルにすることを狙いとした非ベイジアン正則化モデルであり、トピックモデルに対する追加正則化(Additive Regularization on Topic Models (ARTM))をベースとしたオープンソースプロジェクトです。BigARTMは、Dirichletの事前仮説はお使いのドキュメントのスパーシティの特徴と競合し、このスパーシティを考慮しようとすると極端に複雑なモデルになってしまうという前提によって同期付けられています。ここでは、BigARTMの背後にある基本原理を説明し、Daily Kosデータセットにどのように適用するのかを説明します。
なぜLDAよりBigARTMが優れているのか?
上述したように、BigARTMはベイジアンのLDAアプローチとは異なり、確率論的非ベイジアンアプローチを採用しています。Konstantin Vorontsov’s and Anna Potapenko’s paper on additive regularizationによると、LDAにおけるDirichletの仮説は、ドキュメントにおける現実世界のトピックの密度には適合しません。BigARTMはLDAと異なり、テキストの完全な生成モデルを構築しようとはしません。代わりに、正則化器(regularizer)を用いて特定の評価指標を最適化しようとします。これらの正則化器はいかなる確率論的解釈を必要としません。このため、BigARTMにおいては複数目的のトピックモデルの数式でより容易になると言えます。
BigARTMの概要
プロブレムステートメント
ドキュメントのコーパスから一連のトピックを学習したいと考えます。トピックは意味のある一連の単語から構成されます。ここでのゴールは、トピックが一連のドキュメントを要約するということです。このために、ここではBigARTMの論文で用いられている用語をまとめさせてください。
D = テキストのコレクションです。個々のドキュメントdはDの要素であり、個々のドキュメントはワード$n_d$のコレクション($w_0, w_1, ...w_d$)です。
W = ボキャブラリのコレクションです。
T = トピックです。ドキュメントdは複数のトピックから構成されるものとします。
ワード(W)、ドキュメント(D)、トピック(T)からなる確率空間からサンプリングします。ワードとドキュメントは観測されますが、トピックは潜在的な変数となります。
用語$n_{dw}$は、ドキュメントdでワードwで出現した回数を意味します。
それぞれのトピックは、ドキュメントと独立してワードを生成するという条件付き独立性の仮説を置きます。これによって以下の式が得られます。
$$p(w|t) = p(w|t, d)$$
この問題は以下の数式に要約されます。
$$p(w|d) = \sum_n p(t|d)p(w|t)$$
ここで我々が本当に推定したいのは、総和項の確率です(すなわち、ドキュメントにおけるトピックの組み合わせ(p(t|d))とトピックにおけるワードの組み合わせ(p(w|d)))。それぞれのドキュメントは、ドメイン固有のトピックと背景となるトピックの組み合わせと考えられます。背景となるトピックは全てのドキュメントに出現し、ドキュメントに対して均一なワードの分布を持つ傾向があります。一方、ドメイン固有のトピックは疎な分布となる傾向があります。
確率論的因数分解
確率論的行列因数分解を通じて、上述の数式の確率の積の項を推定します。積の項は行列として表現されます。このプロセスは、因数分解の結果としてユニークでなソリューションではないことに注意してください。このため、ソリューションに用いられる初期化に基づいて学習トピックは変化します。
ここでは、ドキュメントdにおけるワードの数wをドキュメントdにおけるワードの数で除算して正規化した$f_{wd}$の要素を持つWxDの次元を持つ$[f_{wd}]$とほぼ等しいデータマトリクスFを作成します。マトリクスFは確率論的に2つのマトリクス$\Theta$と$\theta$に分解されます。
$$F \approx [\phi][\theta]$$
$[\phi]$はトピックに対するワードの確率のマトリクスに対応します。WxTの次元となります。
$[\theta]$はドキュメントに対するトピックの確率のマトリクスに対応します。TxDの次元となります。
3つのマトリクスは全て確率論的であり、以下のようにしてカラムが得られます。
$[\phi]_t$はトピックにおけるワードを表現し、$[\theta]_d$はドキュメントにおけるトピックを表現します。
トピックの数は通常ドキュメントの数やワードの数より少なくなります。
LDA
LDAにおいては、$\phi$と$\theta$は、ハイパーパラメーター$\alpha$と$\beta$から得られるDirichlet分布から導かれると仮定されるカラム$[\phi]_t$と$[\theta]_d$を持ちます。
$\beta$ = $[\beta_w]$、これはワード数に対応するハイパーパラメーターのベクトルとなります。
$\alpha$ = $[\alpha_t]$、これはトピック数に対応するハイパーパラメーターのベクトルとなります。
尤度及び追加正則化
ソリューションを得るために最大化したい対数尤度は以下の式で計算されます。これは、Probabilistic Latent Semantic Analysis (PLSA)における目的関数と同じものであり、BigARTMのスタート地点となります。
ここでは、それぞれのドキュメントにおける全てのワードの結合確率の積の対数を最大化します。ベイズ理論を適用することで上述の数式の右項の総和項が得られます。BigARTMにおいては、$\phi$と$\theta$の関数と正則化係数である$\tau_i$の積となる正則化項のrを追加します。
ここで$R_i$は、我々が導入しようとする正則化のタイプに依存して、いくつか異なる形態を取る正則化器関数となります。一般的な2つのタイプは以下の通りです。
- スムージング正則化
- スパーシング正則化
両方のケースにおいて、正則化器の関数としてKL Divergenceを使用します。様々な目的に対してこれら2つの正則化器を組み合わせることができます。他のタイプにはdecorrelation regularizationとcoherence regularizationがあります(http://machinelearning.ru/wiki/images/4/47/Voron14mlj.pdf の数式34と数式40)。最終的な目的関数は以下のようになります。
$$L(\phi, \theta) + Regularizer$$
スムージング正則化
スムージング正則化は、背景トピックがドメイン固有トピックと比較して均一な分布を持つように背景トピックを平滑化するために用いられます。スムージング正則化においては以下を行います。
- $[\phi]_t$の項と固定分布$\beta$の間のKL Divergenceを最小にする
- $[\theta]_d$の項と固定分布$\alpha$の間のKL Divergenceを最小にする
- 正則化器の項を得るために(1)と(2)の項を加算する
ここでは、必要な$\alpha$、$\beta$の分布にトピック分布、ワード分布がそれぞれ近くなるようにKL Divergenceを最小化します。
少ないトピックに対するスパーシング戦略
少ない数のトピックを得るためには、スパーシング戦略を適用します。これにより、バックグラウンドのトピックのワードではなく、ドメイン固有トピックのワードを選択できるようになります。スパーシング正則化においては以下を行います。
- $[\phi]_t$の項と一様分布の間のKL Divergenceを最大にする
- $[\theta]_d$の項と一様分布の間のKL Divergenceを最大にする
- 正則化器の項を得るために(1)と(2)の項を加算する
我々は、最も高いエントロピー(最大の不確実性)を持つ一様分布からのKL Divergenceを最大化することで、最小のエントロピー(あるいは少ない不確実性)を持つワード、トピックの分布を得ようとしています。これによって、よりピーキーなトピック、ワード分布を得ることができます。
モデル品質
ARTMモデルの品質は以下の指標で評価されます。
- パープレキシティ:モデルによって得られるデータの尤度に対して逆比例します。パープレキシティが小さいほど優れたモデルとなりますが、パープレキシティが10程度の場合、ドキュメントに対して現実的であることが実験で検証されています。
- スパーシティ:$\phi$、$\theta$のマトリクスにおけるゼロ要素のパーセンテージを計測する指標です。
- バックグラウンドワードの割合:高いバックグラウンドワードの比率はモデルの劣化を示しており、良い停止条件となります。これは、スパーシングのやりすぎや、トピックの削除しすぎが原因である場合があります。
- コヒーレンス:これはモデルの解釈可能性を計測するために用いられます。トピックの再頻出ワードがドキュメントで一緒に出現するのであれば、トピックがコヒーレントであると考えられます。コヒーレンスはPointwise Mutual Information (PMI)を用いて計算されます。トピックのコヒーレンスは以下のように計測されます。
- トピックでの頻出ワード
kを取得(通常10に設定) - 上のステップで取得したワードリストから得られるワードのペアに対するPointwise Mutual Information (PMI)を計算
- すべてのPMIの平均を計算
- トピックでの頻出ワード
- カーネルサイズ、純度、コントラスト:カーネルはあるトピックを他のトピックから区別するワードのサブセットで定義されます($W_t = {w: p(t|w) > \delta}$、ここで$\delta$は0.25程度が選択されます)。カーネルのサイズは20から200の値に設定されます。タームの純度とコントラストは以下のように定義されます。
これはトピックのカーネルの全てのワードの確率の総和となります。
トピックモデルにおいては、純度もコントラストが高いほど優れたモデルとなります。
BigARTMライブラリの活用
データファイル
BigARTMライブラリはBigARTMウェブサイトから取得でき、pipでインストールできます。サンプルデータファイルをダウンロードし、以下のように解凍します。ここで使用するデータセットはDaily Kosデータセットです。
wget https://s3-eu-west-1.amazonaws.com/artm/docword.kos.txt.gz
wget https://s3-eu-west-1.amazonaws.com/artm/vocab.kos.txt
gunzip docword.kos.txt.gz
LDA
必要とするパラメーターが少なく、よいベースラインとなるので、まず初めにLDAの実装を見てみます。小規模データセットに対してはfit_offlineメソッド、大規模データセットに対してはfit_onlineメソッドを使用します。コレクションに対するパスの数や、単一ドキュメントに対するパスの数を設定することができます。
import artm
batch_vectorizer = artm.BatchVectorizer(data_path='.', data_format='bow_uci',collection_name='kos', target_folder='kos_batches')
lda = artm.LDA(num_topics=15, alpha=0.01, beta=0.001, cache_theta=True, num_document_passes=5, dictionary=batch_vectorizer.dictionary)
lda.fit_offline(batch_vectorizer=batch_vectorizer, num_collection_passes=10)
top_tokens = lda.get_top_tokens(num_tokens=10)
for i, token_list in enumerate(top_tokens):
print('Topic #{0}: {1}'.format(i, token_list))
Topic #0: ['bush', 'party', 'tax', 'president', 'campaign', 'political', 'state', 'court', 'republican', 'states']
Topic #1: ['iraq', 'war', 'military', 'troops', 'iraqi', 'killed', 'soldiers', 'people', 'forces', 'general']
Topic #2: ['november', 'poll', 'governor', 'house', 'electoral', 'account', 'senate', 'republicans', 'polls', 'contact']
Topic #3: ['senate', 'republican', 'campaign', 'republicans', 'race', 'carson', 'gop', 'democratic', 'debate', 'oklahoma']
Topic #4: ['election', 'bush', 'specter', 'general', 'toomey', 'time', 'vote', 'campaign', 'people', 'john']
Topic #5: ['kerry', 'dean', 'edwards', 'clark', 'primary', 'democratic', 'lieberman', 'gephardt', 'john', 'iowa']
Topic #6: ['race', 'state', 'democrats', 'democratic', 'party', 'candidates', 'ballot', 'nader', 'candidate', 'district']
Topic #7: ['administration', 'bush', 'president', 'house', 'years', 'commission', 'republicans', 'jobs', 'white', 'bill']
Topic #8: ['dean', 'campaign', 'democratic', 'media', 'iowa', 'states', 'union', 'national', 'unions', 'party']
Topic #9: ['house', 'republican', 'million', 'delay', 'money', 'elections', 'committee', 'gop', 'democrats', 'republicans']
Topic #10: ['november', 'vote', 'voting', 'kerry', 'senate', 'republicans', 'house', 'polls', 'poll', 'account']
Topic #11: ['iraq', 'bush', 'war', 'administration', 'president', 'american', 'saddam', 'iraqi', 'intelligence', 'united']
Topic #12: ['bush', 'kerry', 'poll', 'polls', 'percent', 'voters', 'general', 'results', 'numbers', 'polling']
Topic #13: ['time', 'house', 'bush', 'media', 'herseth', 'people', 'john', 'political', 'white', 'election']
Topic #14: ['bush', 'kerry', 'general', 'state', 'percent', 'john', 'states', 'george', 'bushs', 'voters']
以下のように、$\phi$、$\theta$の値を抽出して調査することができます。
phi = lda.phi_ # size is number of words in vocab x number of topics
theta = lda.get_theta() # number of rows correspond to the number of topics
print(phi)
topic_0 topic_1 ... topic_13 topic_14
sawyer 3.505303e-08 3.119175e-08 ... 4.008706e-08 3.906855e-08
harts 3.315658e-08 3.104253e-08 ... 3.624531e-08 8.052595e-06
amdt 3.238032e-08 3.085947e-08 ... 4.258088e-08 3.873533e-08
zimbabwe 3.627813e-08 2.476152e-04 ... 3.621078e-08 4.420800e-08
lindauer 3.455608e-08 4.200092e-08 ... 3.988175e-08 3.874783e-08
... ... ... ... ... ...
history 1.298618e-03 4.766201e-04 ... 1.258537e-04 5.760234e-04
figures 3.393254e-05 4.901363e-04 ... 2.569120e-04 2.455046e-04
consistently 4.986248e-08 1.593209e-05 ... 2.500701e-05 2.794474e-04
section 7.890978e-05 3.725445e-05 ... 2.141521e-05 4.838135e-05
loan 2.032371e-06 9.697820e-06 ... 6.084746e-06 4.030099e-08
print(theta)
1001 1002 1003 ... 2998 2999 3000
topic_0 0.000319 0.060401 0.002734 ... 0.000268 0.034590 0.000489
topic_1 0.001116 0.000816 0.142522 ... 0.179341 0.000151 0.000695
topic_2 0.000156 0.406933 0.023827 ... 0.000146 0.000069 0.000234
topic_3 0.015035 0.002509 0.016867 ... 0.000654 0.000404 0.000501
topic_4 0.001536 0.000192 0.021191 ... 0.001168 0.000120 0.001811
topic_5 0.000767 0.016542 0.000229 ... 0.000913 0.000219 0.000681
topic_6 0.000237 0.004138 0.000271 ... 0.012912 0.027950 0.001180
topic_7 0.015031 0.071737 0.001280 ... 0.153725 0.000137 0.000306
topic_8 0.009610 0.000498 0.020969 ... 0.000346 0.000183 0.000508
topic_9 0.009874 0.000374 0.000575 ... 0.297471 0.073094 0.000716
topic_10 0.000188 0.157790 0.000665 ... 0.000184 0.000067 0.000317
topic_11 0.720288 0.108728 0.687716 ... 0.193028 0.000128 0.000472
topic_12 0.216338 0.000635 0.003797 ... 0.049071 0.392064 0.382058
topic_13 0.008848 0.158345 0.007836 ... 0.000502 0.000988 0.002460
topic_14 0.000655 0.010362 0.069522 ... 0.110271 0.469837 0.607572
ARTM
このAPIはARTMの完全な機能を提供しますが、柔軟性が得られる一方、手動でメトリクスやパラメーターを指定する必要があります。
model_artm = artm.ARTM(num_topics=15, cache_theta=True, scores=[artm.PerplexityScore(name='PerplexityScore', dictionary=dictionary)], regularizers=[artm.SmoothSparseThetaRegularizer(name='SparseTheta', tau=-0.15)])
model_plsa.scores.add(artm.TopTokensScore(name='TopTokensScore', num_tokens=6))
model_artm.scores.add(artm.SparsityPhiScore(name='SparsityPhiScore'))
model_artm.scores.add(artm.TopicKernelScore(name='TopicKernelScore', probability_mass_threshold=0.3))
model_artm.scores.add(artm.TopTokensScore(name='TopTokensScore', num_tokens=6))
model_artm.regularizers.add(artm.SmoothSparsePhiRegularizer(name='SparsePhi', tau=-0.1))
model_artm.regularizers.add(artm.DecorrelatorPhiRegularizer(name='DecorrelatorPhi', tau=1.5e+5))
model_artm.num_document_passes = 1
model_artm.initialize(dictionary=dictionary)
model_artm.fit_offline(batch_vectorizer=batch_vectorizer, num_collection_passes=15)
There are a number of metrics available, depending on what was specified during the initialization phase. You can extract any of the metrics using the following syntax.
model_artm.scores
[PerplexityScore, SparsityPhiScore, TopicKernelScore, TopTokensScore]
model_artm.score_tracker['PerplexityScore'].value
[6873.0439453125,
2589.998779296875,
2684.09814453125,
2577.944580078125,
2601.897216796875,
2550.20263671875,
2531.996826171875,
2475.255126953125,
2410.30078125,
2319.930908203125,
2221.423583984375,
2126.115478515625,
2051.827880859375,
1995.424560546875,
1950.71484375]
$\phi$、$\theta$のマトリクスを取得するためにmodel_artm.get_theta()やmodel_artm.get_phi()を使用することができます。ドキュメントコーパスにおけるトピックのタームを抽出することができます。
for topic_name in model_artm.topic_names:
print(topic_name + ': ',model_artm.score_tracker['TopTokensScore'].last_tokens[topic_name])
topic_0: ['party', 'state', 'campaign', 'tax', 'political', 'republican']
topic_1: ['war', 'troops', 'military', 'iraq', 'people', 'officials']
topic_2: ['governor', 'polls', 'electoral', 'labor', 'november', 'ticket']
topic_3: ['democratic', 'race', 'republican', 'gop', 'campaign', 'money']
topic_4: ['election', 'general', 'john', 'running', 'country', 'national']
topic_5: ['edwards', 'dean', 'john', 'clark', 'iowa', 'lieberman']
topic_6: ['percent', 'race', 'ballot', 'nader', 'state', 'party']
topic_7: ['house', 'bill', 'administration', 'republicans', 'years', 'senate']
topic_8: ['dean', 'campaign', 'states', 'national', 'clark', 'union']
topic_9: ['delay', 'committee', 'republican', 'million', 'district', 'gop']
topic_10: ['november', 'poll', 'vote', 'kerry', 'republicans', 'senate']
topic_11: ['iraq', 'war', 'american', 'administration', 'iraqi', 'security']
topic_12: ['bush', 'kerry', 'bushs', 'voters', 'president', 'poll']
topic_13: ['war', 'time', 'house', 'political', 'democrats', 'herseth']
topic_14: ['state', 'percent', 'democrats', 'people', 'candidates', 'general']
まとめ
多くのユースケースにおいて、LDAがトピックモデリングのスタート地点になる傾向があります。この記事では、最先端の代替案としてBigARTMを紹介しました。BigARTMの背後にある基本原則をライブラリの活用方法とともに説明しました。BigARTMを試して、皆様のニーズに合うかどうかをみて見ることをお勧めします!
添付ノートブックを試してみてください。
ノートブックの日本語訳