概要
本記事はCPUの仕組みを、その中心的な構成要素である演算論理ユニット (ALU : Arithmetic Logic Unit) に焦点を当てて理解する記事です。ALUを構成するLSIとして74HC181 (4ビットALU) について、その基本的な機能と動作原理を解説します。最終的には、74HC181をブレッドボード上で動かし、実際の演算がどのように行われるかを検証することで、CPUの核となる仕組みを体感的に理解することを目的とします。
はじめに
昨今のプログラム開発ではCPUを意識する必要性はありません。しかし、その恩恵を十分に受けているからこそ、CPUの動作原理を知る意義があると思います。
CPUと聞くと一見複雑そうに見えますが、掘り下げていくと実は単純なロジックゲートの集合体であり、処理を一つ一つ分解すれば十分に理解可能です。技術の根幹にある仕組みをなんとなくではなく、理解の積み重ねとして捉え直すことで一つ今後の考え方が変わるのではないでしょうか。
本記事はCPUの中のコア要素であるALUについてブレッドボード上で動かし理解を深めます。
1. CPUの全体構成とALUの役割
CPUとして最小限必要な機能ブロックが以下の図になります。制御回路は入力された命令を解読し、各部に指示を出します。ALUは計算を行う中枢で、入力データやレジスタ(A・B)に一時保存された値を演算します。計算結果は外部へ出力されるほか、再びレジスタに保存され次の処理に利用されたりします。

この中心にあるALUが、加算、減算、論理積、論理和などのすべての演算処理を一手に引き受ける「CPUの中の頭脳」になります。
2. 74HC181の概要:4ビットALUの入出力
74HC181はALUのロジックICです。制御信号の切り替えにより、加減算などの「算術演算」と、ANDやORなどの「論理演算」を実行できます。複数個つなげて8ビットや16ビットへ拡張できるのですが、今回はCPUの原理を理解するため、最小限の4ビットの入出力計算を実行してみます。
※今回は回路のわかりやすさを重視するため、H=1, L=0とする『正論理』として解説します。データシートを確認する際には、負論理表記と混同しないよう注意してください。
- ピンの種類と機能
| ピン | 機能 |
|---|---|
| A, B | 4ビット入力、演算対象となるデータ |
| S0-S3 | 4ビットセレクタ、実行する演算を選択するための信号 |
| M | モード制御、算術演算と論理演算を切り替える信号 |
| F | 4ビット出力の演算結果 |
| Cn | キャリー(繰り上がり)入力 |
| Cn+4 | キャリー(繰り上がり)出力 |
- 演算処理(キャリーなし)
| S3 | S2 | S1 | S0 | 論理演算(M:1) | 算術演算(M:0) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | $F = \overline{A}$ | $F = A$ Minus $1$ |
| 0 | 0 | 0 | 1 | $F = \overline{A}B$ | $F = AB$ Minus $1$ |
| 0 | 0 | 1 | 0 | $F = \overline{A} + B$ | $F = A\overline{B}$ Minus $1$ |
| 0 | 0 | 1 | 1 | $F = 1$ | $F = $ Minus $1$ (2の補数) |
| 0 | 1 | 0 | 0 | $F = \overline{A + B}$ | $F = A$ Plus $(A + \overline{B})$ |
| 0 | 1 | 0 | 1 | $F = \overline{B}$ | $F = AB$ Plus $(A + B)$ |
| 0 | 1 | 1 | 0 | $F = \overline{A \oplus B}$ | $F = A$ Minus $B$ Minus $1$ |
| 0 | 1 | 1 | 1 | $F = A + \overline{B}$ | $F = A + \overline{B}$ |
| 1 | 0 | 0 | 0 | $F = \overline{A} B$ | $F = A$ Plus $(A + B)$ |
| 1 | 0 | 0 | 1 | $F = A \oplus B$ | $F = A$ Plus $B$ |
| 1 | 0 | 1 | 0 | $F = B$ | $F = A\overline{B}$ Plus $(A + B)$ |
| 1 | 0 | 1 | 1 | $F = A + B$ | $F = A + B$ |
| 1 | 1 | 0 | 0 | $F = 0$ | $F = A$ Plus $A$ |
| 1 | 1 | 0 | 1 | $F = A \overline{B}$ | $F = AB$ Plus $A$ |
| 1 | 1 | 1 | 0 | $F = AB$ | $F = A\overline{B}$ Plus $A$ |
| 1 | 1 | 1 | 1 | $F = A$ | $F = A$ |
3. 74HC181の動作検証(ブレッドボードシミュレーション)
74HC181をブレッドボードに実装し、電源(VCC/GND)を接続します。その後、入力(A, B, S, M, Cn)に信号を入力し、出力(F, Cn+4)の計算結果を確認します。
- A OR B (0b0100 OR 0b0010) 結果 : F (0b0110)

- A AND B (0b0110 AND 0b0010) 結果 : F (0b0010)

- A Plus B (0b0110 Plus 0b0010) 結果 : F (0b1000)

4. ALUにない演算を実行するためには
では、ALUにない演算をするにはどうしたらいいでしょうか。そのためにはALUが実行可能な単純な命令を、複数回組み合わせて実行することで実現できます。
乗算は、基本的に「加算の繰り返し」で実現できます。 具体的には、乗数を2進数にし、最下位ビット(0ビット目)から順に確認します。そのビットが「1」であれば加算し、「0」であれば何もしません。 次のビットへ進むごとに被乗数を2倍(左シフト)していき、乗数の全ビットを確認し終えた時点の合計が、最終的な計算結果となります。
2 x 3 の計算
【ステップ 0】初期値
レジスタA: 2
レジスタB: 0
乗数 : 0b0011 (3)
【ステップ 1】 乗数の1ビット目が1なのでAにBを足して結果をBに入れる
ALU演算: レジスタA : 2 + レジスタB : 0 -> レジスタB: 2

【ステップ 2】 Aを倍にする
ALU演算: レジスタA : 2 + レジスタA : 2 -> レジスタA : 4
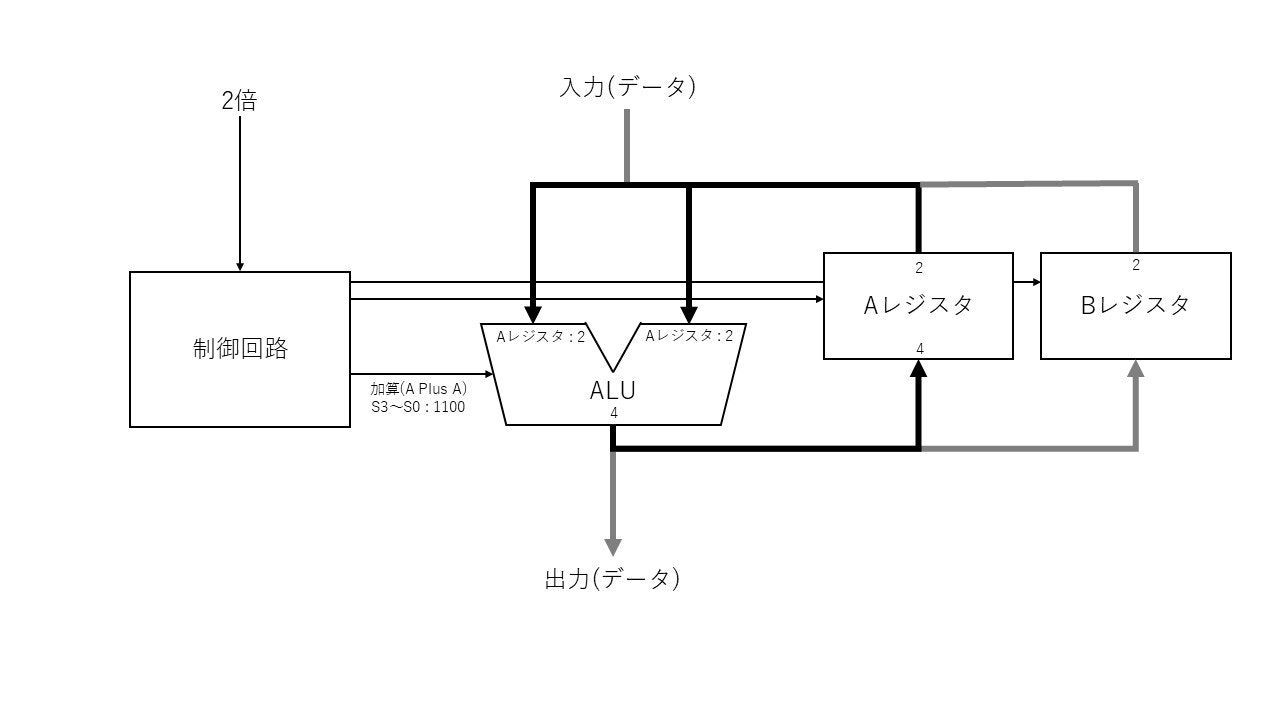
【ステップ 3】 乗数の2ビット目が1なのでAにBを足して結果をBに入れる
ALU演算: レジスタA : 4 + レジスタB : 2 -> レジスタB : 6
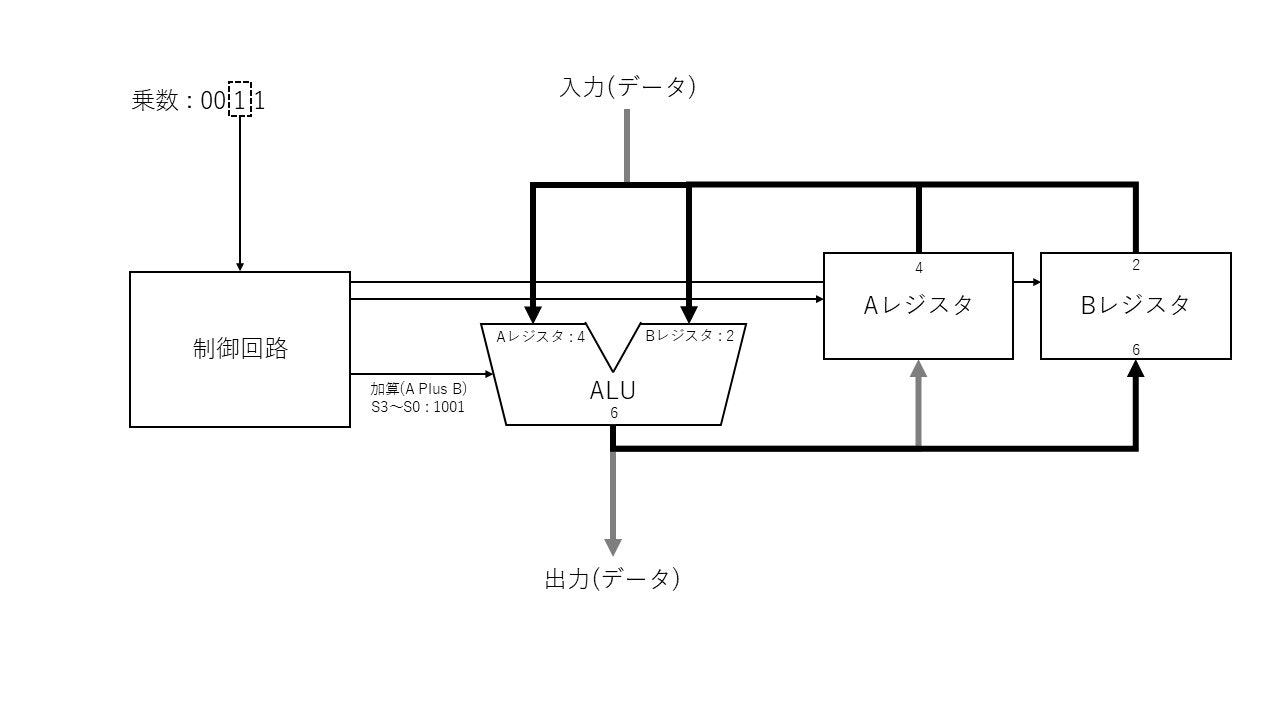
【ステップ 4】 Aを倍にする。
ALU演算: レジスタA : 4 + レジスタA : 4 -> レジスタA : 8

【ステップ 5】 乗数の3ビット目が0なのでなにもしない
【ステップ 6】 Aを倍にする。
ALU演算: レジスタA : 8 + レジスタA : 8 -> レジスタA : 16
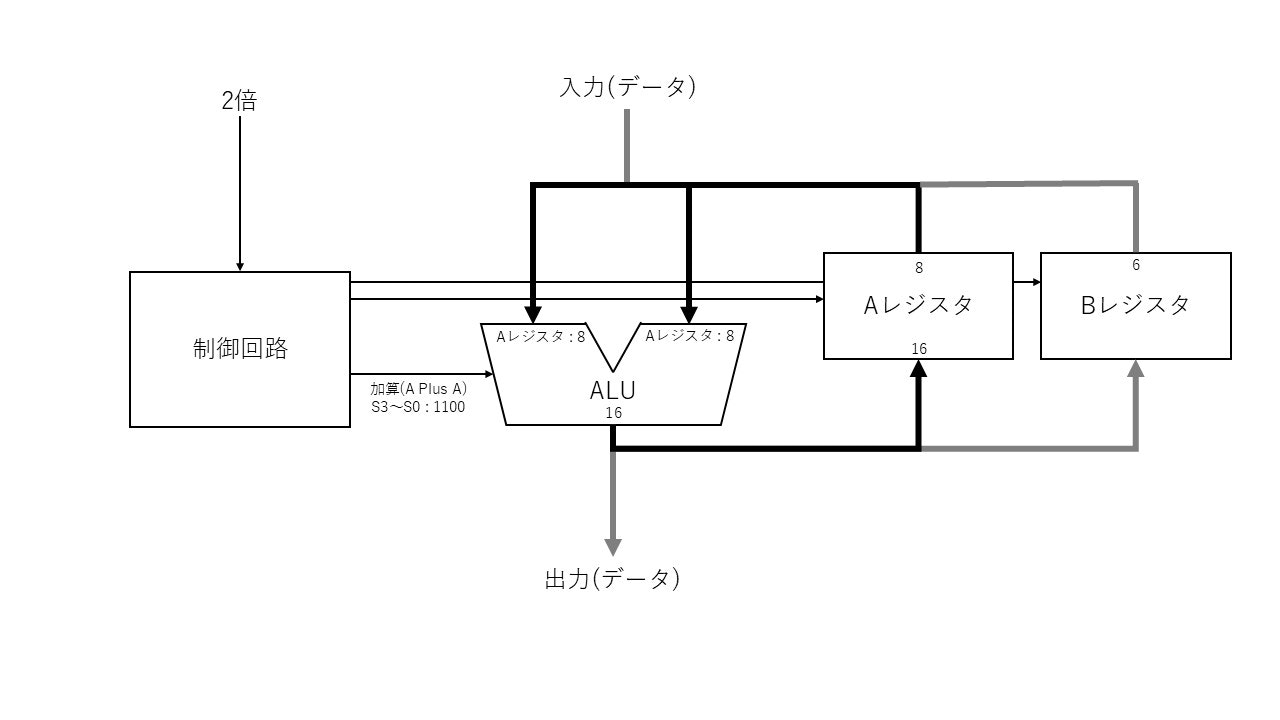
【ステップ 7】 乗数の4ビット目が0なので何もしない
【結果】レジスタBの値 : 6が計算の結果になります
同様に、除算を行いたい場合は、「減算」を組み合わせるアルゴリズムを用いることで計算できます。さらに高度な計算も、すべて整数の加減算とビット操作の手順に分解可能です。
ただし、上記演算でわかるように乗算に7ステップかかっています。このALUと上記周辺回路だと加算に比べて乗算は7倍時間がかかるということです。そこで、もっと高度なCPUでは乗算器などの専用回路をALUに組み込むことで、演算の高速化を図っています。
まとめ
74HC181を使って、CPUのALUが加算や論理演算を物理的にどう実現しているか紐解いていきました。
今後は、74HC181の周辺にレジスタ・メモリ・プログラムカウンタなどを実際に作っていき、完全なCPUを作成したいと思います。