ALifeで地形浸食のシミュレートに挑戦する

きっかけ

社内勉強会でO'ReillyのALife本 (https://www.oreilly.co.jp/books/9784873118475/ )をやった。
そこで前から興味があった地形の浸食を練習がてらやってみることにした。

環境

Python+Matplotlib

処理の流れをざっくりと

1. 地面高度のモデル(2次元配列)を作る
2. 雨量のモデル(2次元配列)を作る
3. 降雨: 雨量のモデルに一様な値を与える
4. 水流: 高度の高い点から低い点に対して雨量を移動させる
5. 浸食: 高度の高い点から低い点に対して（雨量に応じて）高度を移動させる
6. 3-5を繰り返す

プログラム

importとクラス定義

# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

class terrain:

初期化と描画関連

    # コンストラクタ
    def __init__ (self, n, alt = 0.0, rainmove = 0.5, terrainmove = 0.1, rainfall = 0.2):
        self.size = n
        # 高度
        self.z = np.zeros((n, n))
        self.z += alt
        # 雨量
        self.r = np.zeros((n, n))
        # そのほか
        self.pos4 = ((1, 0), (-1, 0), (0, 1), (0, -1))
        self.pos8 = ((1, 0), (-1, 0), (0, 1), (0, -1), (1, 1), (-1, 1), (-1, 1), (-1, -1))
        self.rainfall = rainfall
        self.rainmove = rainmove
        self.terrainmove = terrainmove
    # 図を初期化
    def init_figure(self, n=1):
        self.fig = plt.figure(figsize=(18, 10))
        self.axs = []
        for cnt in range(n):
            ax_h = self.fig.add_subplot(2, n, cnt + 1)
            ax_r = self.fig.add_subplot(2, n, n + cnt + 1)
            self.axs.append((ax_h, ax_r))
    # 高度と降雨を描画
    def plot(self, idx = 0):
        # 高度情報と降雨情報
        za = np.array(self.z)
        ra = np.array(self.r)
        # 座標たち
        x = np.linspace(0, 1.0, za.shape[1])
        y = np.linspace(0, 1.0, za.shape[0])
        mx, my = np.meshgrid(x, y)
        # 高度Mesh
        surf = self.axs[idx][0].pcolormesh(mx, my, za, cmap="terrain", vmin = 0.0, vmax = 1.0)          
        self.fig.colorbar(surf, ax=self.axs[idx][0])
        # 水位Mesh
        surf = self.axs[idx][1].pcolormesh(mx, my, ra, cmap="jet", vmin = 0.0, vmax = 1.0)   # "GnBu"
        self.fig.colorbar(surf, ax=self.axs[idx][1])        

初期値まわり

    # ガウスで山を作る 
    def add_ridge(self, path, sigma = 0.2, alt = 0.2):
        for p in path:     
            g = self.get_gauss(p[0], p[1], sigma, alt)
            self.z = np.maximum(self.z, g)
    # 高度に乱数を足しこむ
    def add_random(self, size):
        self.z += self.get_random(size)
    # ガウス
      def get_gauss(self, cx, cy, sigma = 0.2, alt = 0.2):
        n = self.size
        dx = cx - n / 2
        dy = cy - n / 2  
        x = np.linspace(-(n + dx) / n, (n - dx) / n, n)
        y = np.linspace(-(n + dy) / n, (n - dx) / n, n)
        x, y = np.meshgrid(x, y)
        z = alt * np.exp(-(x ** 2 + y ** 2) / (2 * sigma ** 2)) / (2 * np.pi * sigma ** 2)
        return z
    # 乱数
    def get_random(self, max):
        np.random.seed(0)
        return np.random.rand(self.size, self.size) * max   

降雨と水流

雨は8方向に拡散する

    # 降雨を計算    
    def update_rain(self):
        dr = np.zeros((self.size, self.size))
        # 降雨
        dr += self.rainfall
        # グリッドをループ
        for iy, xlist in enumerate(self.z):
            for ix, x in enumerate(xlist):
                lows = []
                for pos in self.pos8:
                    tx = (ix + pos[0]) % self.size
                    ty = (iy + pos[1]) % self.size
                    # "下流"を算出
                    if self.z[iy, ix] > self.z[ty, tx]:
                        lows.append((ty, tx))
                for low in lows:
                    move = self.rainmove * self.r[iy, ix] / len(lows)
                    dr[iy, ix] -= move
                    dr[low[0], low[1]] += move
        # 蒸発1
        #dr -= 0.18
        # 雨を足しこむ
        self.r += dr;
        # 蒸発2
        self.r /= 2

浸食

浸食は4方向に発生する
この降雨は8方向、浸食は4方向とすることで、ALifeにあった拡散の速度を表現しようとしている。

    # 浸食を計算
    def update_erosion(self):
        for iy, xlist in enumerate(self.z):
            for ix, x in enumerate(xlist):
                lows = []
                #if self.r[iy, ix] < 0.10:
                #    continue
                for pos in self.pos4:
                    # from + to
                    tx = (ix + pos[0]) % self.size
                    ty = (iy + pos[1]) % self.size
                    # 浸食発生の条件
                    if self.z[iy, ix] > self.z[ty, tx]:
                        lows.append((ty, tx))
                for low in lows:
                    # 高度の差分に比例して削る場合
                    #move = (self.z[iy, ix] - self.z[ty, tx]) / 10
                    # 雨量に比例して削る場合
                    move = self.terrainmove * self.r[iy, ix] / len(lows)
                    self.z[iy, ix] -= move
                    self.z[low[0], low[1]] += move

メイン

if __name__ == "__main__":
    # インスタンスを生成
    tr = terrain(50)
    # 図は3組
    tr.init_figure(3)
    # 初期値を与える
    tr.add_ridge([(25, 25)], sigma = 0.4, alt = 0.4)
    tr.add_ridge([(10, 40), (25, 35), (40, 40)])
    tr.add_random(0.01)
    # 初期状態をplot
    tr.plot(0)
    # 演算1回目
    for n in range(50):
        tr.update_rain()
        tr.update_erosion()
    tr.plot(1)
    # 演算2回目    
    for n in range(50):
        tr.update_rain()
        tr.update_erosion()
    tr.plot(2)
    # showして終了
    plt.show()

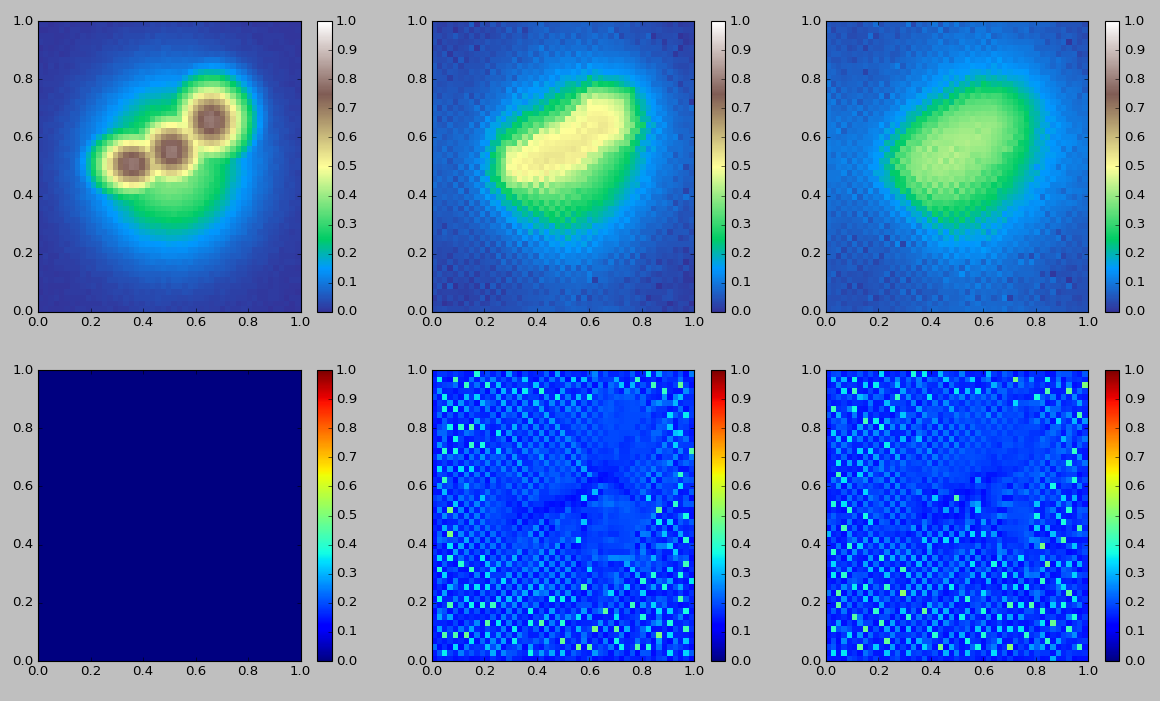
実行結果

• 山がなくなって扇状地ができようとしている
• 川ができるのを期待していたができていない

今回は必ず高度の高いほうから低いほうに高度(土壌)が移動する処理にしたため、川なんぞできる前に土壌が平坦に形成されてしまうようだ。

今後、川ができる仕組みを盛り込めたら面白そう。

プログラム全体

# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

class terrain:
    # コンストラクタ
    def __init__ (self, n, alt = 0.0, rainmove = 0.5, terrainmove = 0.1, rainfall = 0.2):
        self.size = n
        # 高度
        self.z = np.zeros((n, n))
        self.z += alt
        # 雨量
        self.r = np.zeros((n, n))
        # そのほか
        self.pos4 = ((1, 0), (-1, 0), (0, 1), (0, -1))
        self.pos8 = ((1, 0), (-1, 0), (0, 1), (0, -1), (1, 1), (-1, 1), (-1, 1), (-1, -1))
        self.rainfall = rainfall
        self.rainmove = rainmove
        self.terrainmove = terrainmove
    # 図を初期化
    def init_figure(self, n=1):
        self.fig = plt.figure(figsize=(18, 10))
        #self.ax1 = self.fig.add_subplot(121, projection='3d')
        self.axs = []
        for cnt in range(n):
            #self.ax2 = self.fig.add_subplot(122, projection='3d')
            ax_h = self.fig.add_subplot(2, n, cnt + 1)
            ax_r = self.fig.add_subplot(2, n, n + cnt + 1)
            self.axs.append((ax_h, ax_r))
    # 高度と降雨を描画
    def plot(self, idx = 0):
        # 高度情報と降雨情報
        za = np.array(self.z)
        ra = np.array(self.r)
        # 座標たち
        x = np.linspace(0, 1.0, za.shape[1])
        y = np.linspace(0, 1.0, za.shape[0])
        mx, my = np.meshgrid(x, y)
        # 高度Mesh
        surf = self.axs[idx][0].pcolormesh(mx, my, za, cmap="terrain", vmin = 0.0, vmax = 1.0)          
        self.fig.colorbar(surf, ax=self.axs[idx][0])
        # 水位Mesh
        surf = self.axs[idx][1].pcolormesh(mx, my, ra, cmap="jet", vmin = 0.0, vmax = 1.0)   # "GnBu"
        self.fig.colorbar(surf, ax=self.axs[idx][1])        
    # ガウスで山を作る 
    def add_ridge(self, path, sigma = 0.2, alt = 0.2):
        for p in path:     
            g = self.get_gauss(p[0], p[1], sigma, alt)
            self.z = np.maximum(self.z, g)
    # 高度に乱数を足しこむ
    def add_random(self, size):
        self.z += self.get_random(size)
    # ガウス
    def get_gauss(self, cx, cy, sigma = 0.2, alt = 0.2):
        n = self.size
        dx = cx - n / 2
        dy = cy - n / 2  
        x = np.linspace(-(n + dx) / n, (n - dx) / n, n)
        y = np.linspace(-(n + dy) / n, (n - dx) / n, n)
        x, y = np.meshgrid(x, y)
        z = alt * np.exp(-(x ** 2 + y ** 2) / (2 * sigma ** 2)) / (2 * np.pi * sigma ** 2)
        return z
    # 乱数
    def get_random(self, max):
        np.random.seed(0)
        return np.random.rand(self.size, self.size) * max
    # 降雨を計算    
    def update_rain(self):
        dr = np.zeros((self.size, self.size))
        # 降雨
        dr += self.rainfall
        # グリッドをループ
        for iy, xlist in enumerate(self.z):
            for ix, x in enumerate(xlist):
                lows = []
                for pos in self.pos8:
                    tx = (ix + pos[0]) % self.size
                    ty = (iy + pos[1]) % self.size
                    # "下流"を算出
                    if self.z[iy, ix] > self.z[ty, tx]:
                        lows.append((ty, tx))
                for low in lows:
                    move = self.rainmove * self.r[iy, ix] / len(lows)
                    dr[iy, ix] -= move
                    dr[low[0], low[1]] += move
        # 蒸発1
        #dr -= 0.18
        # 雨を足しこむ
        self.r += dr;
        # 蒸発2
        self.r /= 2
    # 浸食を計算
    def update_erosion(self):
        for iy, xlist in enumerate(self.z):
            for ix, x in enumerate(xlist):
                lows = []
                #if self.r[iy, ix] < 0.10:
                #    continue
                for pos in self.pos4:
                    # from + to
                    tx = (ix + pos[0]) % self.size
                    ty = (iy + pos[1]) % self.size
                    # 浸食発生の条件
                    if self.z[iy, ix] > self.z[ty, tx]:
                        lows.append((ty, tx))
                for low in lows:
                    # 高度の差分に比例して削る場合
                    #move = (self.z[iy, ix] - self.z[ty, tx]) / 10
                    # 雨量に比例して削る場合
                    move = self.terrainmove * self.r[iy, ix] / len(lows)
                    self.z[iy, ix] -= move
                    self.z[low[0], low[1]] += move


# main
if __name__ == "__main__":
    # インスタンスを生成
    tr = terrain(50)
    # 図は3組
    tr.init_figure(3)
    # 初期値を与える
    tr.add_ridge([(25, 25)], sigma = 0.4, alt = 0.4)
    tr.add_ridge([(10, 40), (25, 35), (40, 40)])
    tr.add_random(0.01)
    # 初期状態をplot
    tr.plot(0)
    # 演算1回目
    for n in range(50):
        tr.update_rain()
        tr.update_erosion()
    tr.plot(1)
    # 演算2回目    
    for n in range(50):
        tr.update_rain()
        tr.update_erosion()
    tr.plot(2)
    # showして終了
    plt.show()