バリデーションについてのメモランダム

モデルのバリデーションについてあまりに忘れるので、最低限覚えておきたいことをまとめる。
この記事では、hold-out法やクロスバリデーションなど主なバリデーション手法と、時系列データの扱いにも少し触れる。
参考文献: Kaggle本

1. 準備

1-1. 環境

記事中のコードは、Windows-10, Python 3.7.3で動作を確認した。

import platform

print(platform.platform())
print(platform.python_version())

1-2. データセット

回帰、二値分類用データセットを、sklearn.datasetsから読み込む。

from sklearn import datasets
import numpy as np
import pandas as pd

# 回帰用データセット
boston = datasets.load_boston()
boston_X = pd.DataFrame(boston.data, columns=boston.feature_names)
boston_y = pd.Series(boston.target)

# 二値分類用データセット
cancer = datasets.load_breast_cancer()
cancer_X = pd.DataFrame(cancer.data, columns=cancer.feature_names)
cancer_y = pd.Series(cancer.target)

2. hold-out法

最も単純で分かりやすい方法である。一部をバリデーション用にとっておいて、残りでモデルを学習する。
よく「7 : 3に分けましょう」などと聞くけれど、考えてみればそんなのデータ量に依存するので決まった比率はない。
バリデーションデータは学習に使えないので、データ量が少ない場合は後述のクロスバリデーション等を検討すべきだし、逆に膨大ならhold-out法で対処すべきだろう。
基本的にはシャッフルしてデータを分割する。ただし、時系列データのときはシャッフルしない。過去の情報から未来を予測しようとしているのに、シャッフルしてしまうとその未来の情報を学習してしまう（リークする）リスクがあるからだ。一度それでエラい目に遭った。
以下は、データを3 : 1に分け、決定係数で評価するコードである。ちなみに、決定係数などの評価指標については以前こちらにまとめた。

from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split

tr_x, va_x, tr_y, va_y = train_test_split(boston_X, boston_y, test_size=0.25, random_state=2020, shuffle=True)
slr = LinearRegression()
slr.fit(tr_x, tr_y)
va_pred = slr.predict(va_x)
score = r2_score(va_y, va_pred)
print(score)

0.732147337324218

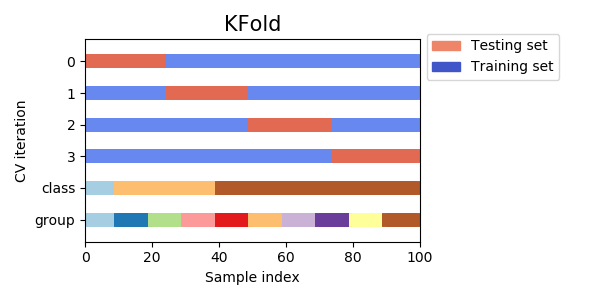
3. クロスバリデーション

先程のhold-out法を複数回繰り返す方法。イメージはロケットえんぴつ。あるブロックでモデルを評価したら、次はそのブロックを学習データに足し込み別のブロックで評価して……をブロックの数だけ繰り返す。
hold-out法ではバリデーションデータを学習に使えないので、データ量が少ない場合はクロスバリデーションを選ぶことが多い。
ブロックの数 = fold数は、増やすほど学習データが増える半面、計算時間も増す。これもデータ量次第だが、4, 5ぐらいが一般的だろう。
モデルの精度（汎化性能）を評価する際は、各foldのスコア平均を見るか、全foldの予測値であらためてスコアを計算すればいい。

以下がクロスバリデーションのコード。hold-out法ほどシンプルじゃないのでいっつも忘れる。

from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import KFold

i = 0
scores = []
kf = KFold(n_splits=4, shuffle=True, random_state=2020)
for tr_idx, va_idx in kf.split(boston_X):
    i += 1
    tr_x, va_x = boston_X.iloc[tr_idx], boston_X.iloc[va_idx]
    tr_y, va_y = boston_y.iloc[tr_idx], boston_y.iloc[va_idx]
    slr = LinearRegression()
    slr.fit(tr_x, tr_y)
    va_pred = slr.predict(va_x)
    score = mean_absolute_error(va_y, va_pred)
    print('fold{}: {:.2f}'.format(i, score))
    scores.append(score)

print(np.mean(scores))

fold1: 3.34
fold2: 3.39
fold3: 3.89
fold4: 3.02
3.4098095699116184

これでバリデーションは完了だが、fold数だけモデルができてしまった。どうにか一つにまとめる必要がある。

• 各foldのモデルの平均をとる。
• あらためてデータ全体でモデルを学習する。

どちらでも構わないだろうが、実務なら後者で作ったモデルを保存・運用すればいいのではないだろうか。

4. stratified k-fold

こちらは分類タスクの際に用いる方法。
例えば、陰性か陽性かに分類するタスクで、陽性が極端に少ないような場合、ランダムにデータ分割したらバリデーションデータに1件も陽性がない、なんてことが起こるかもしれない。
そこで、foldごとに含まれるクラスの割合が等しくなるよう層化抽出 (stratified sampling) したいというモチベーションが生まれる。
逆に、割合が均衡ならあまり気にすることはない。

from sklearn.linear_model import LogisticRegression
from sklearn.metrics import log_loss
from sklearn.model_selection import StratifiedKFold

# hold-out法でも可能
# tr_x, va_x, tr_y, va_y = train_test_split(cancer_X, cancer_y, test_size=0.25, random_state=2020, shuffle=True, stratify=cancer_y)

i = 0
scores = []
kf = StratifiedKFold(n_splits=4, shuffle=True, random_state=2020)
for tr_idx, va_idx in kf.split(cancer_X, cancer_y):
    i += 1
    tr_x, va_x = cancer_X.iloc[tr_idx], cancer_X.iloc[va_idx]
    tr_y, va_y = cancer_y.iloc[tr_idx], cancer_y.iloc[va_idx]
    lr = LogisticRegression(solver='liblinear')
    lr.fit(tr_x, tr_y)
    va_pred = lr.predict_proba(va_x)[:, 1]
    score = log_loss(va_y, va_pred)
    print('fold{}: {:.2f}'.format(i, score))
    scores.append(score)

print(np.mean(scores))

fold1: 0.11
fold2: 0.17
fold3: 0.09
fold4: 0.07
0.11030074372001544

5. その他のバリデーション

その他、使ったことないけどこんなのあるんだ、ということで手法だけメモしておく。

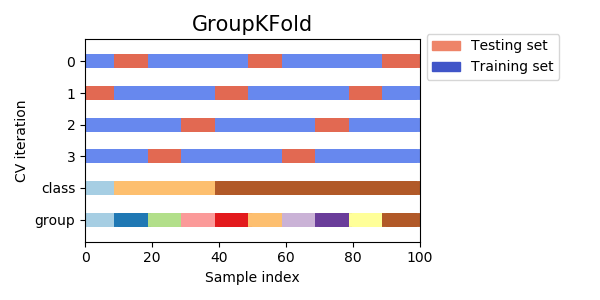
5-1. group k-fold

グループを表す変数でデータを分割する手法。例えば、顧客単位の購買履歴を学習し、新規顧客をスコアリングするといったタスクの場合、学習データとバリデーションデータに同一顧客が混在してほしくない。答えが一部学習データに混ざってしまう (リーク) と考えられるからである。
そこで、顧客IDを使ってデータを分割したい、といったときにgroup k-foldを行う。
GroupKFoldというクラスが使える。ただしシャッフルと乱数シードの機能がない。

5-2. leave-one-out (LOO)

これも使ったことがない。極端にデータが少なく、N数を目一杯増やしたい → レコード数だけfold数を増やしてしまえ、という過激な手法らしい。
KFoldでn_splitsにレコード数を指定すればいいだけだが、LeaveOneOutという専用のクラスもある。

6. 時系列データのバリデーション

ここまで扱ってきた手法を、そのまま時系列データに用いてはならない、ということがこの記事で最も重要なことかもしれない。
古い / 新しいということはそれだけで情報なので、学習や評価の際も必ず時系列は意識しなければならない。

6-1. データセット

sklearn.datasetsにはちょうどいい時系列データがないので、ここではSIGNATEの【練習問題】お弁当の需要予測データを使う。
※規約的に使っていいか分からなかったので問い合わせたところ「非営利目的の場合に限り分析結果やソースコードの公開は可能」との回答を頂いた。優しい。
チュートリアルに沿って以下加工を行う。

• 傾向が異なる古い (5月以前の) データは除外
• 特徴量として、日数、お楽しみメニューフラグ、カレーフラグを作成

import matplotlib.pyplot as plt
%matplotlib inline

# データ読み込み
train = pd.read_csv('./train.csv')

# 傾向が異なる古いデータを除外
train.index = pd.to_datetime(train['datetime'])
train = train['2014-05-01':].copy()

# プロット
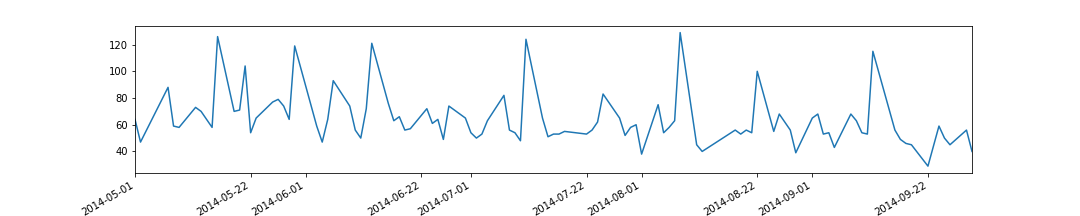
train['y'].plot(figsize=(15, 3))
plt.show()

# 特徴量作成
train = train.reset_index(drop=True)
train['days'] = train.index
train['fun'] = train['remarks'].apply(lambda x: 1 if x == 'お楽しみメニュー' else 0)
train['curry'] = train['name'].apply(lambda x: 1 if x.find('カレー') >= 0 else 0)
train_X = train[['days', 'fun', 'curry']].copy()
train_y = train['y'].copy()

基本的には右肩下がりの販売数 (日数と負の相関) だが、人気メニュー (お楽しみメニュー、カレー) 時にスパイクしている。
単純な線形回帰でどこまで予測できるだろうか。

from sklearn.metrics import mean_squared_error

slr = LinearRegression()
slr.fit(train_X, train_y)
train['pred'] = slr.predict(train_X)
rmse = np.sqrt(mean_squared_error(train['y'], train['pred']))

print(rmse)
train.plot(y=['y', 'pred'], figsize=(15, 3))
plt.show()

10.548692191381326

だいぶ外れているが、大まかな傾向は掴めている。
残差と他の特徴量との関係を見たい気持ちをぐっとこらえ、バリデーションの話題に戻る。

6-2. 時系列データのクロスバリデーション

最もシンプルなのは、シャッフルしないhold-out法だろう。train_test_split関数の引数shuffleにFalseを指定すればいい。古いデータで学習し、新しいデータで評価することで、時系列データでも問題なくバリデーションすることができる。
ただし、直近の、つまり最近の傾向を最もよく反映しているであろうデータを学習に使わないのはやはりもったいない。
そのため、汎化性能を確かめられたらあらためて全データで再学習する場合が多いだろう。
それでも、他の期間に対しても精度が出るのかとか、単純にデータ量が足りないとか、つまりもっと効率的にデータを使いたいという不満が残るはずだ。
そこで、TimeSeriesSplitという手法が登場する。発想自体は単純で、要するに時系列的順序を守ってクロスバリデーションする方法だ。

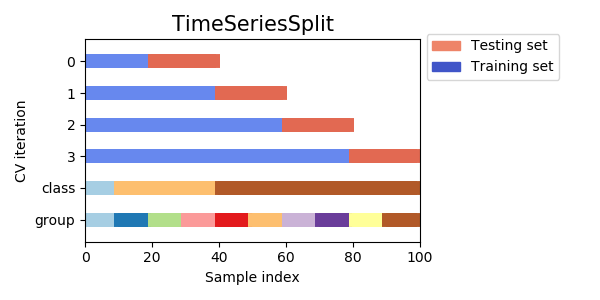
しかしこれにしたって、やっぱり直近のデータは使えないじゃないかとか、foldごとに学習データの長さが違うとか、不満は残る。だが使えるに越したことはない。

from sklearn.model_selection import TimeSeriesSplit

i = 0
scores = []
tss = TimeSeriesSplit(n_splits=4)
for tr_idx, va_idx in tss.split(train_X):
    i += 1
    tr_x, va_x = train_X.iloc[tr_idx], train_X.iloc[va_idx]
    tr_y, va_y = train_y.iloc[tr_idx], train_y.iloc[va_idx]
    slr = LinearRegression()
    slr.fit(tr_x, tr_y)
    va_pred = slr.predict(va_x)
    score = np.sqrt(mean_squared_error(va_y, va_pred))
    print('fold{}: {:.2f}'.format(i, score))
    scores.append(score)

print(np.mean(scores))

fold1: 20.29
fold2: 9.21
fold3: 15.05
fold4: 9.68
13.557202833084698

なかなか判断に困る結果だ。学習データを増やすほど精度が良くなっている、というわけでもないのが面白い。色々と試す余地は残っているが、この記事のスコープを超えるためここで終える。

このように、どうにも時系列データのバリデーションははっきりとした結論を下すのが難しい。とくに、事実直近にトレンドの変化が起こっているような場合、学習データでバリデーションデータを説明できない方が正しいのであって、むしろバリデーションデータでモデルを学習すべき状況と言える。
制御系なんかでは、RMSEか何かで精度を監視しておいて、閾値を下回ったら既存制御に戻し、必要数データが溜まったら再学習して制御を再開する、なんて運用がありえるだろう。あるいは、オンライン学習でモデルを更新し続けるという考えもあるかもしれない。
需要予測系はどうなのだろうか。必ずしもコンペみたいに一定期間を予測しなければならないわけでもないだろうから、短期の自己相関を考慮したARIMAモデルなども有力だろう。今度需要予測チームに聞いてみたい。