タスクごとの評価指標についてあまりに忘れるので、最低限覚えておきたいことをまとめる。
この記事では、回帰と二値分類の主な評価指標を扱う。
参考文献: Kaggle本
1. 準備
1-1. 環境
記事中のコードは、Windows-10, Python 3.7.3で動作を確認した。
import platform
print(platform.platform())
print(platform.python_version())
1-2. データセット
回帰、二値分類用データセットを、sklearn.datasetsから読み込む。
from sklearn import datasets
import numpy as np
import pandas as pd
# 回帰用データセット
boston = datasets.load_boston()
boston_X = pd.DataFrame(boston.data, columns=boston.feature_names)
boston_y = pd.Series(boston.target)
# 二値分類用データセット
cancer = datasets.load_breast_cancer()
cancer_X = pd.DataFrame(cancer.data, columns=cancer.feature_names)
cancer_y = pd.Series(cancer.target)
1-3. モデリング
評価指標を得るため、テキトウにモデリングし、予測値を出力する。
本当に評価指標を得るためだけなので、EDAも特徴量作成もバリデーションすらしていない。罪悪感が凄い。
from sklearn.linear_model import LinearRegression, LogisticRegression
# 回帰
slr = LinearRegression()
slr.fit(boston_X, boston_y)
boston_y_pred = slr.predict(boston_X)
# 二値分類
lr = LogisticRegression(solver='liblinear')
lr.fit(cancer_X, cancer_y)
cancer_y_pred = lr.predict(cancer_X)
cancer_y_pred_prob = lr.predict_proba(cancer_X)[:, 1]
2. 回帰タスクの評価指標
RMSE (Root Mean Squared Error: 平均平方二乗誤差)
$$
\mathrm{RMSE}=\displaystyle\sqrt{\dfrac{1}{N}\sum_{i=1}^N(y_i-\hat{y}_i)^2}
$$
予測値がどれだけ真の値から外れているのか直感的に把握できるので、実務でもよく使っている。
メジャーな評価指標なのに、sklearnはMSEしかサポートしていない。np.sqrtしてから返してくれればいいのに。
from sklearn.metrics import mean_squared_error
rmse = np.sqrt(mean_squared_error(boston_y, boston_y_pred))
print(rmse)
4.679191295697281
MAE (Mean Absolute Error)
$$
\mathrm{MAE}=\dfrac{1}{N}\displaystyle\sum_{i=1}^N|y_i-\hat{y}_i|
$$
隣のチームがこれを評価指標にしていた。私は使ったことがない。
RMSEと比べて、外れ値の影響が少ない。RMSEが平均なら、MAEは中央値というイメージ。
from sklearn.metrics import mean_absolute_error
mae = mean_absolute_error(boston_y, boston_y_pred)
print(mae)
3.2708628109003115
決定係数
R^2=1-\dfrac{\sum_{i=1}^N(y_i-\hat{y}_i)^2}{\sum_{i=1}^N(y_i-\bar{y})^2}
1に近づくほど精度が高いという、まさに文系のためにあるような指標。
そのため昔は大好きだったが、一度実務で痛い目を見てからあまり信用しなくなった。
決定係数は分母が分散なので、データのバラツキが大きければテキトウなモデルでも割と高く出る。
参考程度に見て、実際の当たり具合はRMSEで判断した方が無難。
from sklearn.metrics import r2_score
r2 = r2_score(boston_y, boston_y_pred)
print(r2)
0.7406426641094095
3. 二値分類タスクの評価指標
二値分類タスクは、正例か負例かの分類結果を予測値とする場合と、正例である確率を予測値とする場合があるので、分けて扱う。
3-1. 分類結果を予測値とする場合
混同行列 (confusion matrix)
- TP (True Positive, 真陽性): 予測値を正例として、その予測が正しい場合
- TN (True Negative, 真陰性): 予測値を負例として、その予測が正しい場合
- FP (False Positive, 偽陽性): 予測値を正例として、その予測が誤りの場合
- FN (False Negative, 偽陰性): 予測値を負例として、その予測が誤りの場合
ただの集計だが、なんだかんだで一番大切ではないだろうか。
例えば、100人に1人しか感染しないウイルスが流行したので、検査を行ったとする。
このとき、とにかく全員を陰性としてしまえば、その精度は一見99%に見えてしまう……みたいなトリックに惑わされないよう、混同行列はしっかり覚えておく必要がある。
なのに、いっつもTPだのFNだのワケが分からなくなる。
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(cancer_y, cancer_y_pred)
tn, fp, fn, tp = cm.flatten()
print(cm)
[[198 14]
[ 9 348]]
accuracy (正答率)
$$
accuracy = \frac{TP+TN}{TP+TN+FP+FN}
$$
error rate (誤答率)
$$
error ; rate = 1-accuracy
$$
先程の例で言えば、全員を陰性とした場合の正答率は0.99となってしまう。
二値分類タスクの場合、まずデータが不均衡かどうかを見なければ何も始まらないことがよく分かる。
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(cancer_y, cancer_y_pred)
print(accuracy)
0.9595782073813708
precision (適合率)
$$
precision = \frac{TP}{TP+FP}
$$
recall (再現率)
$$
recall = \frac{TP}{TP+FN}
$$
precisionは正例と予測したもののうち真の値も正例の割合、recallは真の値が正例のもののうちどの程度を正例と予測したかの割合。
両者はトレードオフの関係にある。precisionは誤検知の割合で、recallは見逃しの割合なので、目的に応じてどちらを重視するか決める。
先程のウイルス検査の例などはrecallを重視するだろうし、マーケティングの文脈ならprecisionが重要になってくるだろう。
from sklearn.metrics import precision_score, recall_score
precision = precision_score(cancer_y, cancer_y_pred)
recall = recall_score(cancer_y, cancer_y_pred)
print(precision)
print(recall)
0.9613259668508287
0.9747899159663865
F1-score
$$
F_1 = \dfrac{2}{\dfrac{1}{recall}+\dfrac{1}{precision}}
$$
Fβ-score
$$
F_\beta = \dfrac{(1+\beta^2)}{\dfrac{\beta^2}{recall}+\dfrac{1}{precision}}
$$
F1-scoreはprecisionとrecallの調和平均、Fβ-scoreはそれをrecallをどれだけ重視するかを表す係数βで調整した指標。
バランスを取っているので使い勝手が良さそうだが、なにぶん実務で使ったことがないのでイメージが湧かない。
from sklearn.metrics import f1_score, fbeta_score
f1 = f1_score(cancer_y, cancer_y_pred)
fbeta = fbeta_score(cancer_y, cancer_y_pred, beta=0.5)
print(f1)
print(fbeta)
0.968011126564673
0.96398891966759
MCC (Matthews Correlation Coefficient)
$$
MCC = \dfrac{TP \times TN - FP \times FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}
$$
寡聞にして聞いたことがない。
-1から1の値をとり、1のときに完璧な予測を、0のときにランダムな予測を、-1のときは完全に反対の予測を行っていると解釈するらしい。
不均衡なデータでも適切に評価しやすいとのことで、是非使えるようになりたい。
from sklearn.metrics import matthews_corrcoef
mcc = matthews_corrcoef(cancer_y, cancer_y_pred)
print(mcc)
0.9132886202215396
3-2. 確率を予測値とする場合
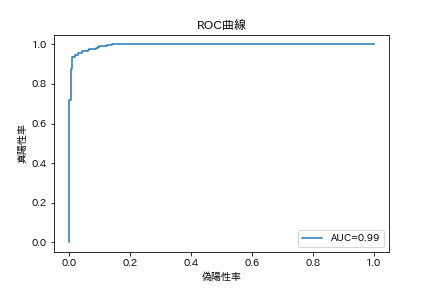
AUC (Area Under the ROC Curve)
横軸に偽陽性率、縦軸に真陽性率をプロットしたROC曲線の、下部の面積。
左から順に予測値が高いレコードを並べ、実際に正例なら上に、負例なら横に進むプロットと考えればいい。
そのため、完全な予測のときROC直線は左上の天井に跳ね上がり、AUCは1となる。ランダムな予測なら対角線上をなぞる。
有名なGini係数は Gini = 2AUC - 1 と表されるため、AUCと線形。
import japanize_matplotlib
import matplotlib.pyplot as plt
from sklearn.metrics import roc_auc_score, roc_curve
%matplotlib inline
auc = roc_auc_score(cancer_y, cancer_y_pred_prob)
print(auc)
fpr, tpr, thresholds = roc_curve(cancer_y, cancer_y_pred_prob)
plt.plot(fpr, tpr, label='AUC={:.2f}'.format(auc))
plt.legend()
plt.xlabel('偽陽性率')
plt.ylabel('真陽性率')
plt.title('ROC曲線')
plt.show()
logloss
$$
logloss = -\frac{1}{N} \sum_{i=1}^N(y_i {\log} p_i+(1-y_i){\log}(1-p_i))
$$
これもAUCと並んで有名。cross entropyとも呼ばれる。
真の値を予測している確率の対数をとり、符号を反転させているので低い方がいい(らしい)
正例である確率を低く見積もったのに正例である場合や、高く見積もったのに負例だった場合にペナルティを与える発想になっている。
from sklearn.metrics import log_loss
logloss = log_loss(cancer_y, cancer_y_pred_prob)
print(logloss)
0.09214591499092101
多クラス分類やレコメンデーションは実務経験がなく、ただ写経するだけになりそうだったので次の機会に譲る。
いつか書けるようになりたい。