はじめに
ChatGPT に質問しながら 2022 年の統計検定 1 級(統計応用・理工学)の問題を解いてみようと思います。
確率に関する基礎的な概念は理解していることを前提に、各種公式や統計用語は積極的に ChatGPT 先生に質問していきます。
まったくの初学者を想定して、ChatGPT に問題を丸投げしてダイレクトに答えを得ようという試みではありません!
問題文は一部省略しています。全文は適切なところで入手してください。(問題) (略解)
また、ChatGPT は問 1 のみ GPT-3.5 を利用しましたが、思ったような答えが得られないことがあったので問 2 以降は GPT-4 を使います。
問 1, 問 2 :
ここ
問 3, 問 4 :
https://qiita.com/taichan003/items/db1bf9195f84c4f1554e
問 5:
https://qiita.com/taichan003/items/322457d7e59d4e1f2548
問 1
ある工場には,同じ部品を製造するための機械 A と機械 B が 1 つずつある。機械 A を使うと 1 日あたり $m$ 個の部品が製造できるが,それぞれの部品は確率 $p \in (0, 1)$ で独立に不良品となる。また機械 B を使うと 1 日あたり $n$ 個の部品を製造できるが,それぞれの部品は確率 $q \in (0, 1)$ で独立に不良品となる。いま,機械 A と機械 B を両方使って合計 $m + n$ 個の部品を製造したとき,この工場の製造責任者は,1 日に生じる不良品の個数 $Z$ がどのくらいになるのかを知りたい。以下の各問に答えよ。
〔1〕 $Z$ の期待値と分散を求めよ。
〔2〕 $Z$ のモーメント母関数 $m_Z(\theta) = E[e^{\theta Z}]$ を求めよ。
〔3〕 $m = 100,p = 0.02,n = 50,q = 0.01$ のとき,チェビシェフの不等式を利用して $P(Z \geq 10)$ を上から評価せよ。
〔4〕 パラメータの設定が上問〔3〕と同じであるとき,ポアソン近似を用いて $P(Z = 0)$ を求めよ。
〔5〕 パラメータの設定が上問〔3〕と同じであるとき,ポアソン近似を用いてモーメント母関数 $m_Z(\theta) = E[e^{\theta Z}]$ を求めよ。さらに,次の定理を用いて $ \log_{10} P(Z \geq 10)$ を上から評価せよ。なお,定理の証明は不要である。
定理:確率変数 $Z$ と正の実数 $a$,$\theta$ に対して,不等式 $P(Z \geq a) ≤ e^{−\theta a}E[e^{\theta Z}]$ が成り立つ。
問 1 (解答)
ChatGPT への質問の全文はこちら:
https://chat.openai.com/share/3aebbf64-009d-43b6-9216-7479fef942a1
※最後の質問への回答は間違っています。参照する場合は注意してください。
〔1〕機械 A, B の不良品数をそれぞれ $N_A$, $N_B$ とする。これらは独立なので $Z=N_A + N_B$ の平均・分散は $N_A$, $N_B$ の平均・分散の和となる。

〔2〕そのまま ChatGPT に聞いても1行目の式で止まってしまう。2行目の式変形を教えたうえでもう一度質問すれば $N_A$ のモーメント母関数が求まる。
\begin{align}
m_{N_A}(t) = E[e^{t N_A}] &= \sum [e^{t k} {}_mC_k \ p^k (1 - p)^{m - k}] \\\
&= \sum [{}_mC_k \ (e^t p)^k (1 - p)^{m - k}] \ \text{(ここは手動で注釈)}\\\
& = (1 - p + e^t p)^m
\end{align}
ちなみに GPT-4 を使えば特に詰まることなく欲しい式が得られた。

さて、求める答えは $Z = N_A + N_B$ のモーメント母関数なので、
\begin{align}
M_Z(t) = M_{N_A}(t) \cdot M_{N_B}(t) = (1 - p + e^t p)^m (1 - q + e^t q)^n.
\end{align}
〔3〕ChatGPT の答えがすごく分かりやすかった。得られた回答に具体的な数字をあてはめればよい。
以下は ChatGPT の回答にわたしが具体的な数字を書き加えたもの。本来の回答はchatGPTへの質問の全文をご参照ください。
チェビシェフの不等式を使用して、確率変数Z = N_A + N_Bの確率 P(Z > T) を評価することができます。
チェビシェフの不等式は、確率変数がどのような分布であっても適用できる一般的な不等式です。
不等式は次のように表されます:
P(|Z - μ| ≥ kσ) ≤ 1/k^2
ここで、Zは確率変数、μはZの平均、σはZの標準偏差です。kは任意の正の定数です。
まず、確率変数Z = N_A + N_Bの平均と分散を計算しましょう:
Zの平均: μ_Z = μ_A + μ_B = 100 * 0.02 + 50 * 0.01 = 2.50
Zの分散: σ^2_Z = σ^2_A + σ^2_B = 100 * 0.02 * 0.98 + 50 * 0.01 * 0.99 = 2.455
次に、チェビシェフの不等式を使用して、P(Z > T) を評価します。
この場合、kσに相当する値をTとし、μ_Zからの距離を考えます:
kσ = |T - μ_Z|
これをkについて解きます:
k = |T - μ_Z| / σ_Z = |10 - 2.5| / √2.455 = 4.78669
ここで、Tを設定し、kを求めます。
一般的なkの値は3や4などが使用されますが、あなたが求める上限に応じて適切なkを選びます。
例えば、k = 4とすると、チェビシェフの不等式は次のようになります:
P(|Z - μ_Z| ≥ 4σ_Z) ≤ 1/4^2 = 1/16
P(|Z - 2.5| ≥ kσ_Z) ≤ 1/k^2 = 0.043644
したがって、P(Z > 10) ≤ 0.043644 です。
この不等式を用いて、ZがTより大きい確率を評価できます。
この評価は、mとnが十分に大きく、pとqが十分に小さい場合に適用できます。
〔4〕前問と同様、こちらも完璧な答え。回答に具体的な数字を書き込んで計算するだけ。
ポアソン近似を使用して、確率変数Z = N_A + N_Bが特定の値(ここでは0)を取る確率 P(Z = 0) を求めることができます。
ポアソン近似は、二項分布が大きな試行回数(mとnが十分に大きい場合)および小さな成功確率(pとqが十分に小さい場合)を持つ場合に適用できます。
ポアソン近似では、N_AとN_Bがそれぞれポアソン分布に近似されます。
ポアソン分布の平均λは、λ = m * p(N_Aの平均)およびλ = n * q(N_Bの平均)となります。
したがって、N_AとN_Bがポアソン分布に従う場合、確率変数Z = N_A + N_Bもポアソン分布に近似されます。
Zの平均λ_Zは、λ_Z = λ_A + λ_B = m * p + n * q です。
ポアソン分布の確率質量関数は以下のように表されます:
P(X = k) = (e^(-λ) * λ^k) / k!
ここで、Xはポアソン分布に従う確率変数です。
したがって、P(Z = 0) を求めるためには、Zの平均λ_Zを使用して次のように計算できます:
P(Z = 0) = (e^(-λ_Z) * λ_Z^0) / 0! = e^(-λ_Z)
したがって、P(Z = 0) は e^(-λ_Z) に等しいです。λ_Zは m * p + n * q ですから、
P(Z = 0) = e^(-(m * p + n * q)) = e^(-(100 * 0.02 + 50 * 0.01)) = 0.082
この式を使用して、確率変数Zが0を取る確率 P(Z = 0) を求めることができます。
ポアソン近似は、mとnが十分に大きく、pとqが十分に小さい場合に適用され、確率を比較的正確に評価できます。
〔5〕 ポアソン分布に従うモーメント母関数が分かればいいが〔2〕と同様にGPT-3.5では定義式を書くだけで終わってしまう。なぜか二項分布のときよりもさらに察しが悪く、かなり誘導しても正しい答えが得られなかったので GPT-4 を利用する。
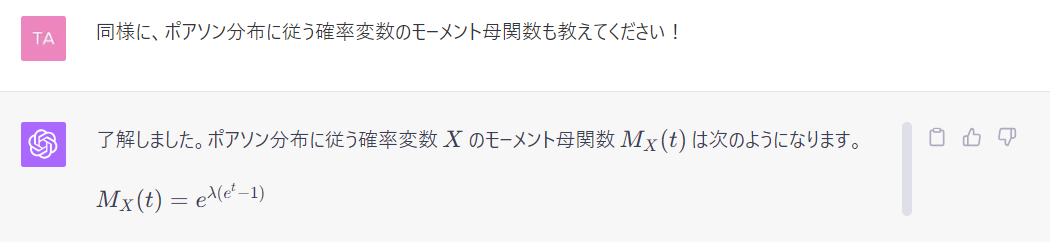
また、後半の問題についてはモーメント母関数が分かればあとは代入して計算するだけなのでとくに ChatGPT は利用しない。
\begin{align}
& m_Z(t) = E[e^{t Z}] = e^{\lambda (e^t - 1)} = \exp (2.5 (e^t - 1)) \\\
& \log_{10} P(Z \geq 10) \leq \log_{10} (e^{-10 t} E[e^{t z}]) = (2.5 e^t - 2.5 - 10t) \cdot \log_{10}e, \ \forall t > 0
\end{align}
(下式最初の不等式は問題文中のヒントによる)
$f(t) := 2.5 e^t - 2.5 - 10t$ とおくと、$f'(t) = 2.5 e^t - 10$ より、$t_0 = \log 4$ のときに最小値 $f(t_0) = -6.3629436112$ をとる。
したがって、
\begin{align}
\log_{10} P(Z \geq 10) \leq f(t_0) \cdot \log_{10} e = -6.3629436112 \cdot 0.4342944819 = -2.76339129899
\end{align}
を得る。
問 2
あるプレス工程において,材料の設定温度 ($x$) と製品の要求品質を達成するまでに必要な加工時間 ($y$) の関係を調べたところ,表 1 のようになった。ただし,各温度における 3 回ずつの実験は,それぞれランダムな順序で行われた。
表 1: 設定温度 ($x$) と加工時間 ($y$)
| 設定温度 | $x = 150$ | $x = 200$ | $x = 250$ | $x = 300$ |
|---|---|---|---|---|
| 加工時間($y$) | 31 | 44 | 45 | 45 |
| 39 | 36 | 41 | 51 | |
| 35 | 31 | 52 | 54 | |
| 平均 | 35.0 | 37.0 | 46.0 | 50.0 |
表 1 のデータに対し,設定温度 ($x$) と加工時間 ($y$) 間に回帰直線を当てはめたところ $y = 17.7+0.108x$ となり,その際の分散分析表の一部は表 2 のようであった。また,設定温度を要因とした一元配置分散分析を行ったところ,分散分析表の一部は表 3 のようであった。以下の各問に答えよ。
表 2: 単回帰分析での分散分析表
| 要因 | 平方和 | 自由度 | 平均平方 |
|---|---|---|---|
| 回帰 | 437.4 | 1 | 437.4 |
| 残差 | 246.6 | 10 | 24.66 |
| 計 | 684.0 | 11 |
表 3: 一元配置分散分析表
| 要因 | 平方和 | 自由度 | 平均平方 |
|---|---|---|---|
| 群間 | 462.0 | 3 | 154.0 |
| 群内 | 222.0 | 8 | 27.75 |
| 計 | 684.0 | 11 |
〔1〕 単回帰式 $y = 17.7+0.108x$ に関する,決定係数,および自由度調整済み決定係数はそれぞれいくらか。
〔2〕 表 2 における回帰の有意性検定は有意水準 1%で有意であるか。その理由と共に答えよ。
〔3〕 表 3 における群間差の有意性検定は有意水準 5%で有意であるか。その理由と共に答えよ。
設定温度 $x_j$ における $i$ 番目の観測値を $y_{ij}$ ($i = 1, 2, 3; j = 1, 2, 3, 4$) とし,$x_j$ の下での 3 個の観測値の標本平均を $\bar{y_j}$, $y$ の全平均を $\bar{y}$,$y_{ij}$ と $x_j$ の間の回帰直線を$y = a + bx$ とすると,観測値 $y_{ij}$ の $\bar{y}$ からの偏差は
\begin{align}
y_{ij} − \bar{y} = \{ (a + bx_j ) − \bar{y} \} + \{ \bar{y_j} − (a + bx_j) \} + \{y_{ij} − \bar{y_j} \}
\end{align}
と { } で囲った 3 つの部分に分解される。
〔4〕 データの分解 (1) の右辺の各項の $i$ および $j$ に関する平方和をそれぞれ (1), (2),(3) としたとき,表 4 の分散分析表の (a) から (i) の値を求め,分散分析表を完成させよ。
表 4: 分散分析表
| 要因 | 平方和 | 自由度 | 平均平方 |
|---|---|---|---|
| (1) | (a) | (d) | (g) |
| (2) | (b) | (e) | (h) |
| (3) | (c) | (f) | (i) |
| 計 | 684.0 | 11 |
〔5〕 上問〔4〕の各数値に基づく (1) および (2) の効果に関する検定結果を踏まえ,この実験データの解析結果から何が分かるかを示せ。
問 2 (解答)
ChatGPT への質問の全文はこちら:
https://chat.openai.com/share/e1c9bc7c-0560-4e13-a652-7241d4f44bf6
知らない用語ばかりなので基本的な質問も多いです。
あと途中まで有意水準の漢字を間違えていました。はずかし![]()
\begin{align}
&R^2 = 437.44 / (437.44 + 246.6) = 0.63949476638 \\\
&R_{adj}^2 = 1 - \left( \frac{n - 1}{n - k - 1} \right) \times (1 - R^2) = 1 - \frac{11}{10} \cdot (1 - 0.6395) = 0.60344424301
\end{align}
\begin{align}
F = \frac{\text{回帰平均平方}}{\text{残差平均平方}} = \frac{437.4 / 1}{246.6 / 10} = 17.7372262774
\end{align}
これが自由度$(1, 10)$のF-分布の分位点と比べて大きいかを調べればよい。
しかし、統計検定の問題文には有意水準 $\alpha=0.01$ に対するF-分布のパーセント表は与えられていない。
これについても GPT 先生に代替案を聞いてしまおう。ちなみに GPT-3.5 ではいい回答が引き出せなかった。

データから得られる統計量が $t = \sqrt{17.7372262774} = 4.21155865178$ であり、
これは自由度 10 の t-分布の有意水準 $\alpha=0.01$ での臨界点 2.764 より大きいため有意水準 1% で有意であると言える。
\begin{align}
F = \frac{\text{群間平均平方}}{\text{群内平均平方}} = \frac{462.0 / 3}{222.0 / 8} = 5.54954954955
\end{align}
であり、自由度$(3,8)$ のF-分布の臨界点 $3.708 \sim 5.409$ くらい(問題文の表にちょうどの自由度の F-分布がない)より大きいため、これは有意水準 5% で有意であると言える。
〔4〕


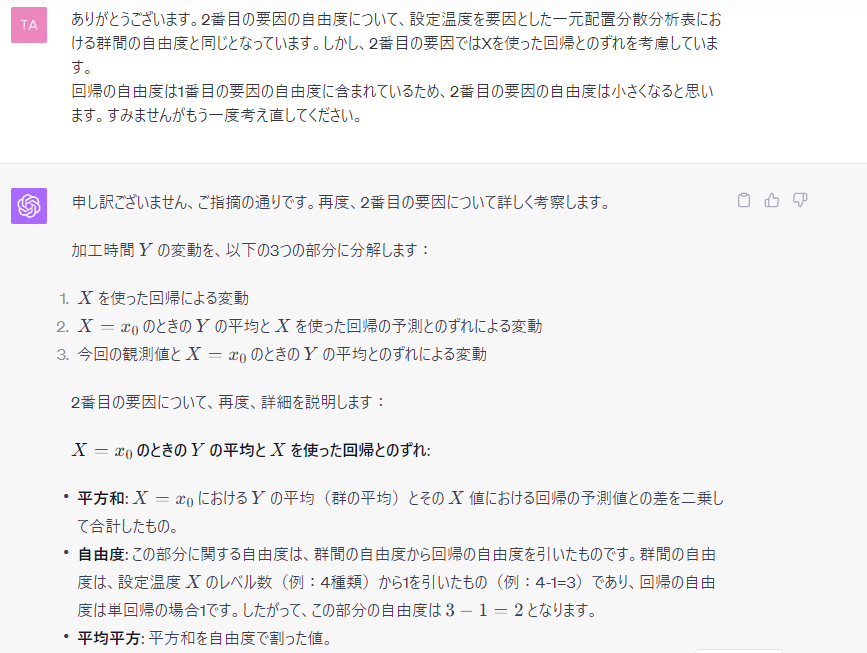
おおよそいい感じの回答だが、自由度の合計がデータ全体の自由度(12 - 1 = 11)より大きくなってしまっている。
それだけを伝えてもしらばくれるだけなので、かなり丁寧に指摘して考え直してもらう必要があった。
原因は 2 番目の要因 $\bar{y_j} − (a + bx_j)$ において $X$ の回帰の自由度をカウントしたため。本来は 1 番目の要因に組み込む代わりに、2番目の要因では考えないという文脈があって、その文脈を ChatGPT は読み取れなかったのだと思う。
数学の世界でも空気を読むという文化があったのだなあと感心した。
〔5〕
1 番目と 2 番目の要因について有意性検定を行う。
\begin{align}
&F_1 = \frac{\text{1番目平均平方}}{\text{群内平均平方}} = \frac{437.4 / 1}{222.0 / 8} = 15.7621621622
\\\
&F_2 = \frac{\text{2番目平均平方}}{\text{群内平均平方}} = \frac{24.6 / 2}{222.0 / 8} = 0.44324324324
\end{align}
自由度$8$のt-分布の有意水準 5% での分位点は $1.860$, $\sqrt{F_1} = 3.97015895931$ は分位点より大きいためこの回帰は有意と言える。
一方、自由度$(2, 8)$のF-分布の有意水準 5% での分位点 $4.103 \sim 5.786$, F-統計量 $F_2 = 0.44324324324$ はこれより小さい。
あとはこの計算結果を ChatGPT に伝えるだけ。ここは ChatGPT の面目躍如といったところ。
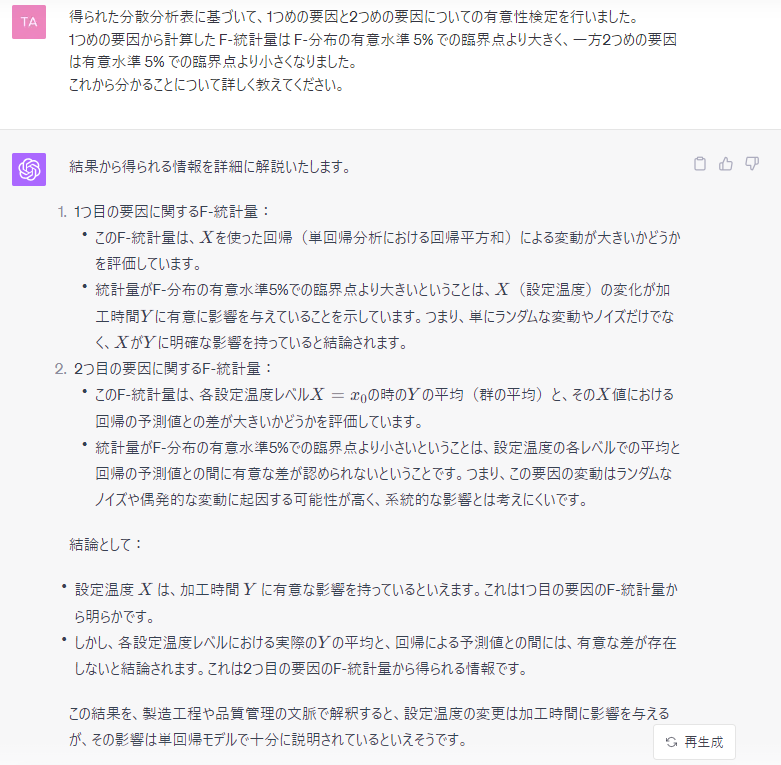
ただし、検定に関する独特の言い回しを勝手にしてくれることはなかったので、利用者側がわきまえている必要がある。

(問 3 以降はこちら)