はじめに
ChatGPT に質問しながら 2022 年の統計検定 1 級(統計応用・理工学)の問題を解いてみようと思います。
確率に関する基礎的な概念は理解していることを前提に、各種公式や統計用語は積極的に ChatGPT 先生に質問していきます。
まったくの初学者を想定して、ChatGPT に問題を丸投げしてダイレクトに答えを得ようという試みではありません!
問題文は一部省略しています。全文は適切なところで入手してください。(問題) (略解)
また、ChatGPT は問 1 のみ GPT-3.5 を利用しましたが、思ったような答えが得られないことがあったので問 2 以降は GPT-4 を使います。
問 1, 問 2 :
https://qiita.com/taichan003/items/3eafd80bc6111697d5ac
問 3, 問 4 :
https://qiita.com/taichan003/items/db1bf9195f84c4f1554e
問 5:
ここ
問 5
ある大企業で,健康診断の一環として従業員の血圧の測定が一定の期間を置いて 2 回行われた。37 歳の昭雄さんは,1 回目の血圧測定で最高血圧(収縮期血圧)が 132mmHg であり,担当の看護師から「血圧が高めなので気を付けてください」と言われた。昭雄さんは,自分なりに節制したところ 2 回目の測定では 128mmHgとなり,4mmHg 下がったと同僚の成美さんに自慢げに言ったところ,彼女に「平均への回帰効果じゃないですか」と言われた。
以下の各問では,この企業の三十代の男性で降圧剤治療を受けていない人たち全体を母集団とする。そして,最高血圧の 1 回目の測定値を $X$,2 回目の測定値を$Y$ とし,$(X, Y)$ は母集団全体で 2 変量正規分布 $N(\mu_X, \mu_Y , \sigma_X, \sigma_Y , \sigma_{XY})$ に従うと仮定する(ここで $\sigma_{XY}$ は $X$ と $Y$ の共分散)。
今回の健康診断の 2 回の血圧測定では,母集団全体での母平均は $\mu_X = \mu_Y = 120$(mmHg),母標準偏差は $\sigma_X = \sigma_Y = 12$(mmHg) であり,$X$ と $Y$ の間の母相関係数 $\rho_{XY}$ は $0.75$ である。
このとき,以下の各問に答えよ。なお,$X = x$ が与えられたときの $Y$ の条件付き分布は $N(\alpha + \beta x, \sigma^2)$ であり,$\beta = \frac{\sigma_{XY}}{\sigma_X^2}$, $\alpha = \mu_X - \beta\mu_X$, $\sigma^2 = \sigma_Y^2 - \frac{\sigma_{XY}^2}{\sigma_X^2}$ となることは用いてよい。
〔1〕 母集団全体における 2 回の血圧の測定値の差 $D = Y − X$ の期待値と分散はいくらか。また,母集団全体で確率 $P(D \leq −4)$ はいくらか。
〔2〕 1 回目の測定値 $X$ が 132mmHg の人の 2 回目の測定値 $Y$ の条件付き期待値$E[Y |X = 132]$ と条件付き分散 $V [Y |X = 132]$ はそれぞれいくらか。この結果をもとに,成美さんの言う「平均への回帰」とは何であるかを簡潔に説明せよ。また,昭雄さんの血圧下降分 4mmHg のうちのどのくらいが平均への回帰分とみなされるであろうか。
平均への回帰の説明のため,次のモデルを想定する。血圧値は測定ごとに変動するが,各人は個人ごとに血圧の真値(その人では定数)$\theta$ を持つとし,各人の測定値は $X = \theta + \varepsilon_1$,$Y = \theta + \varepsilon_2$ と表されるとする。そして $\theta$ は,母集団全体では $N(\mu, \tau^2)$ に従って分布しているとする。ここで $\varepsilon_1$,$\varepsilon_2$ は互いに独立かつ $\theta$ とも独立に,それぞれ $N(0, \psi^2)$ に従う確率変数である。
〔3〕 上記のモデルの下で,$X$ および $Y$ の母集団全体での各分散 $V[X]$,$V[Y]$ および共分散 $Cov[X, Y]$ はそれぞれ $\tau$ と $\psi$ の関数としてどのように表現されるか。また,$X$ および $Y$ の標準偏差ならびに $X$ と $Y$ の間の相関係数が設問の値であるとき,分散 $\tau^2$ と $\psi^2$ はそれぞれいくらか。
〔4〕 1回目の測定値が $X = 132$ の人たち全体では,血圧の真値 $\theta$ はどのように分布しているか。すなわち,$X = 132$ が与えられた下での $\theta$ の条件付き分布は何であり,その条件付き期待値 $E[\theta|X = 132]$ および条件付き分散 $V [\theta|X = 132]$ はそれぞれいくらか。
〔5〕 血圧の真値 $\theta$ が上問〔4〕の分布に従うとき,$X = 132$ の人たちの 2 回目の測定値 $Y$ の分布は何か。この結果から,上記のモデルの下で平均への回帰現象を説明せよ。昭雄さんの 2 回目の測定値は 128mmHg であったが,$X = 132$ の人たちの中で,2 回目の血圧の測定値 $Y$ が 128mmHg 以下となる確率 $P(Y \leq 128|X = 132)$ はいくらか。
問 5 (解答)
ChatGPT への質問の全文はこちら:
https://chat.openai.com/share/3de59c6f-6433-4fe5-aebb-cb6abec1eebe
〔1〕 計算方法を質問する。条件付き分散の計算を詳しく教えてもらったが、$X$ と $Y$ の分散に分割できればあとは問題文にある数字を代入するだけでいい。教えてもらった式を使って計算しても別にいいけど。

回答に具体的な数値を代入する。
\begin{align}
E[Y - X] &= E[Y] - E[X] = \mu_X - \mu_Y = 0, \\\
\\\
V[Y−X] &= V[Y] + V[X] − 2 Cov(Y,X) \\\
&= \sigma_X^2 + \sigma_Y^2 - 2 \cdot \rho_{XY}\sigma_X\sigma_Y = 72.
\end{align}

ChatGPT 先生の教えにより $D := Y - X$ は正規分布に従うので、$Z \sim N(0,1)$ に対し、
\begin{align}
P(D \leq -4) = P(Z \geq 4/\sqrt{72}) \approx P(Z \geq 0.47) \approx 0.32.
\end{align}
〔2〕 前半の計算問題はこちらで行う。
\begin{align}
E[Y | X = 132] &= \alpha + \beta \cdot 132 \\\
V[Y | X = 132] &= \sigma^2
\end{align}
ここで、$\beta = \rho_{XY} = 0.75$, $\alpha = 128 - 0.75 \cdot 128 = 32$, $\sigma^2 = 12^2 - 0.75^2 \cdot 12^2 = 63$ を代入して、
\begin{align}
E[Y | X = 132] = 129, \
V[Y | X = 132] = 63
\end{align}
を得る。
後半の問題について、平均への回帰という言葉の説明はすべて ChatGPT にお任せする。人間の下手な説明はもはや不要。

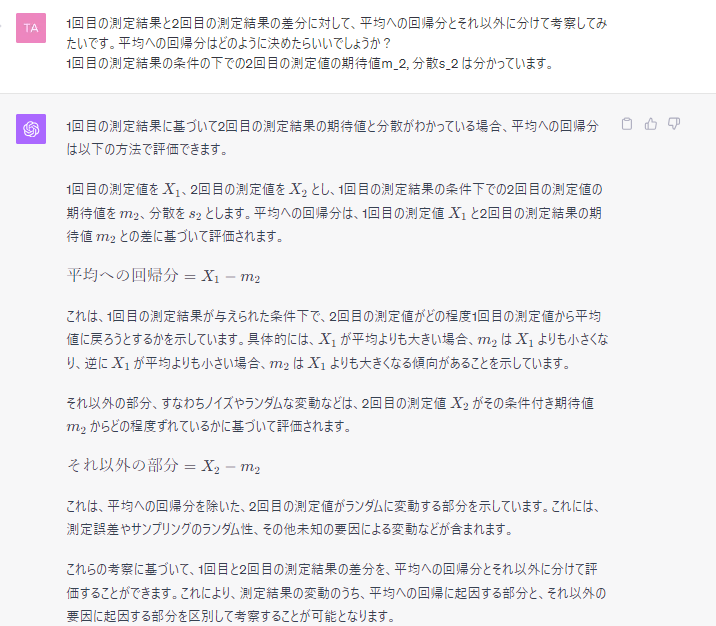
平均への回帰分の決め方は ChatGPT 先生の考察により
\begin{align}
\text{平均への回帰分} = E[Y | X = 132] - 132 = -3
\end{align}
となる。
〔3〕 すでに正規分布の和の平均・分散の公式は教えてもらっているが、共分散とあわせて改めてもう一度質問する。
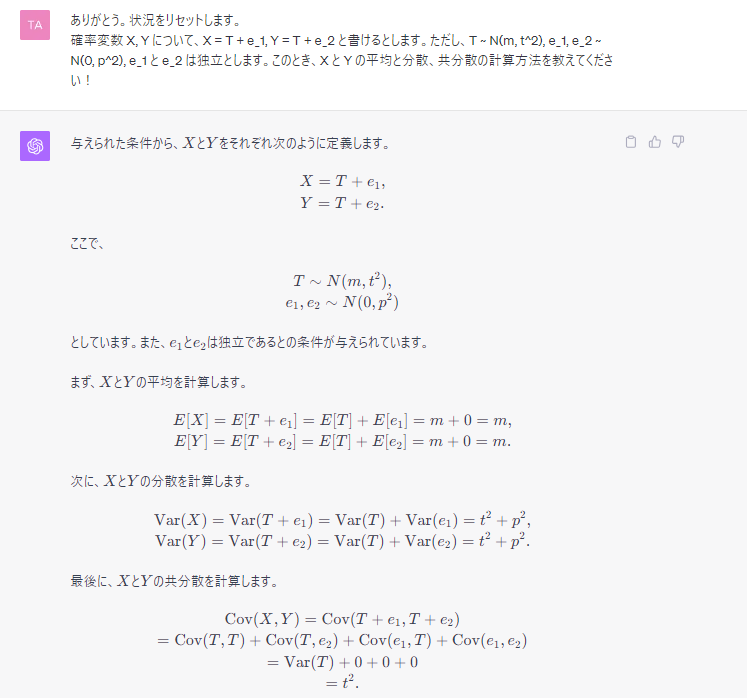
以上を整理して
\begin{align}
V[X] = V[Y] &= \tau^2 + \psi^2 \\\
Cov[X, Y] &= \tau^2
\end{align}
より、$V[X] = 12^2$, $Cov[X, Y] = 0.75 \cdot 12^2$ のとき $\tau^2 = 108$, $\psi^2 = 36$ となる。
〔4〕
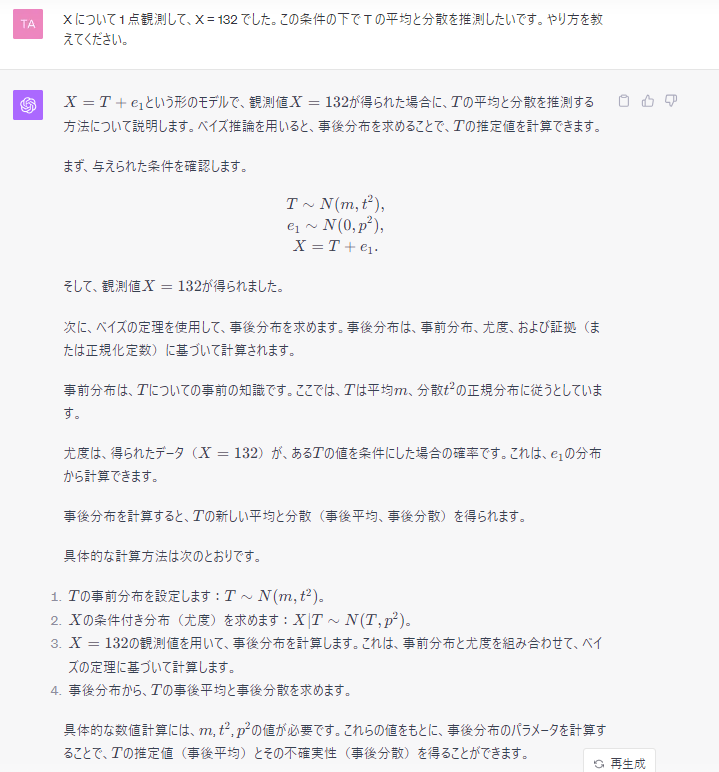

ChatGPT 先生の計算式に $\mu$, $\tau$, $\psi$ を代入する。
\begin{align}
E[\theta | X=132] &= \frac{\frac{\mu}{\tau^2} + \frac{132}{\psi^2}}{\frac{1}{\tau^2} + \frac{1}{\psi^2}} = \frac{\frac{120}{108} + \frac{132}{36}}{\frac{1}{108} + \frac{1}{36}} = 129 ,\\\
V[\theta | X=132] &= \frac{1}{\frac{1}{\tau^2} + \frac{1}{\psi^2}} = \frac{1}{\frac{1}{108} + \frac{1}{36}} = 27 + 36 = 63.
\end{align}
〔5〕 やっていることは〔2〕と同じだから $Y$ の平均と分散も当然同じはずだけど、一応計算しておく。

あとは計算式に具体的な数値を入力する。
\begin{align}
E[Y | X=132] &= E[\theta| X=132] + E[\varepsilon_2] = 129 ,\\\
V[\theta | X=132] &= V[\theta| X=132] + V[\varepsilon_2] = 63.
\end{align}
後半の平均への回帰についての説明は ChatGPT 先生にお任せする。ただし〔2〕と同じ答えにならないよう、問題の意図を汲んで誘導する必要がある。ChatGPT は平均への回帰という答えが見えているだけに、別の観点から答えさせようとするのは意外とめんどくさい。

また、$Z \sim N(0,1)$ に対し、
\begin{align}
P(Y \leq 128 | X=132) = P(Z \geq 1/\sqrt{63}) \approx P(Z \geq 0.13) \approx 0.45.
\end{align}
ちょこっと感想
ChatGPT は確かにすごいけど、統計の仕事をすべてやってくれる夢のツールではないことがよく分かりました。本記事にはいい感じの答えを掲載していますが、裏には無数の失敗した質問が積みあがっています。あと、わたしの自信がなかった問 3 で特に苦労したので、結局質問者の技量に依存するのだと思いました。
ただ、今回は記事の見栄えのために ChatGPT くんには 100 点の答えを要求していましたが、短い質問を積み重ねて途中で人間が察する余地を入れたりすればもう少しやりやすかったはずです。
わたしが来月受験予定のため統計応用の理工学の問題だけやってみました。統計数理や他の科目はたぶんやりません。そろそろまじめに勉強しなくちゃ。。。