はじめに
「Pythonで体験するベイズ推論」を読んで行くうちに疑問があり、コーディングしたものの備忘録です
良い書籍なので興味のある方は是非ご購読を
変化点検出とは
「ある時点でCMを打った結果、パーセプションがあがり売り上げが上がった」
「ある時点で部品の故障があった結果、不良品率が上がった」
など時系列データでは外的・内的要因によってトレンドが変化することがあります。
変化点検出ではそういった変化が生じた「ある時点」を検出する仕組みとなります
まずは変化時点を知り、そこから原因を追求していったりしますね
ベイズを用いた変化点検出(実際=予想)
それではPyMCを使って、ベイズを用いた変化点検出をやってみましょう
まず疑似データを用意します
ここではポワソン分布に従って、2回変化するダミーデータを作ります
a = np.random.poisson(lam=10, size=100)
b = np.random.poisson(lam=5, size=50)
c = np.random.poisson(lam=15, size=120)
data = np.hstack((a,b,c))
n = len(data)
plt.bar(np.arange(n), data, color='r')
plt.xlim(0,n)
plt.show()

さあデータはできたので推定して見ましょう
まずは変化点が実データと同じ2つだと仮定したモデルを組みます
データの事前分布確率もポワソン分布(パラメータλは指数分布)
変化点τは離散一様分布としましょう
alpha = 1.0 / data.mean()
lambda_1 = pm.Exponential("lambda_1", alpha)
lambda_2 = pm.Exponential("lambda_2", alpha)
lambda_3 = pm.Exponential("lambda_3", alpha)
tau = pm.DiscreteUniform("tau", lower=0, upper=n-1)
tau_2 = pm.DiscreteUniform("tau_2", lower=0, upper=n)
@pm.deterministic
def lambda_(tau=tau, tau_2=tau_2, lambda_1=lambda_1, lambda_2=lambda_2, lambda_3=lambda_3):
out = np.zeros(n)
out[:tau] = lambda_1
out[tau:tau_2] = lambda_2
out[tau_2:] = lambda_3
return out
observation = pm.Poisson("obs", lambda_, value=data, observed=True)
model = pm.Model([observation, lambda_1, lambda_2, lambda_3, tau, tau_2])
mcmc = pm.MCMC(model)
mcmc.sample(40000, 10000)
さあこれでベイズ推定は終わりました
結果はどうなったでしょう?
まずはポワソン分布のパラメータλの事後確率分布を見て見ます
lambda_1_samples = mcmc.trace('lambda_1')[:]
lambda_2_samples = mcmc.trace('lambda_2')[:]
lambda_3_samples = mcmc.trace('lambda_3')[:]
tau_samples = mcmc.trace('tau')[:]
tau_2_samples = mcmc.trace('tau_2')[:]
plt.hist(lambda_1_samples, histtype='stepfilled', normed=True, label="posteriro of $\lambda_1$")
plt.hist(lambda_2_samples, histtype='stepfilled', normed=True, label="posteriro of $\lambda_2$")
plt.hist(lambda_3_samples, histtype='stepfilled', normed=True, label="posteriro of $\lambda_3$")
plt.xlim([0,18])
plt.ylim([0,1.6])
plt.show()

綺麗ですね!
実データともあっています
ではτはというと、、、
plt.hist(tau_samples, label="posteriro of $\tau$")
plt.hist(tau_2_samples, label="posteriro of $\tau_2$")
plt.show()

うん、こちらも想定とほぼ同じですで推測はうまく言っているようです
ベイズを用いた変化点検出(実際<>予想)
先ほどの結果は潜在因子を見事に推定していて素晴らしい結果でした
これを使えばもう完璧です!!!
、、、とはまあ現実行かないものです
実際はこんなにはっきり変化点があることは多くなく、もっと混沌としています
また変換点もいくつかあるかなんてぱっと見ではわからないことも多いです
では変化点が想定と異なった場合はどうなるのでしょうか?
まずは変化点が本来より少ない場合(1件)を見てましょう
alpha = 1.0 / data.mean()
lambda_1 = pm.Exponential("lambda_1", alpha)
lambda_2 = pm.Exponential("lambda_2", alpha)
tau = pm.DiscreteUniform("tau", lower=0, upper=n)
@pm.deterministic
def lambda_(tau=tau, lambda_1=lambda_1, lambda_2=lambda_2):
out = np.zeros(n)
out[:tau] = lambda_1
out[tau:] = lambda_2
return out
observation = pm.Poisson("obs", lambda_, value=data, observed=True)
model = pm.Model([observation, lambda_1, lambda_2, tau])
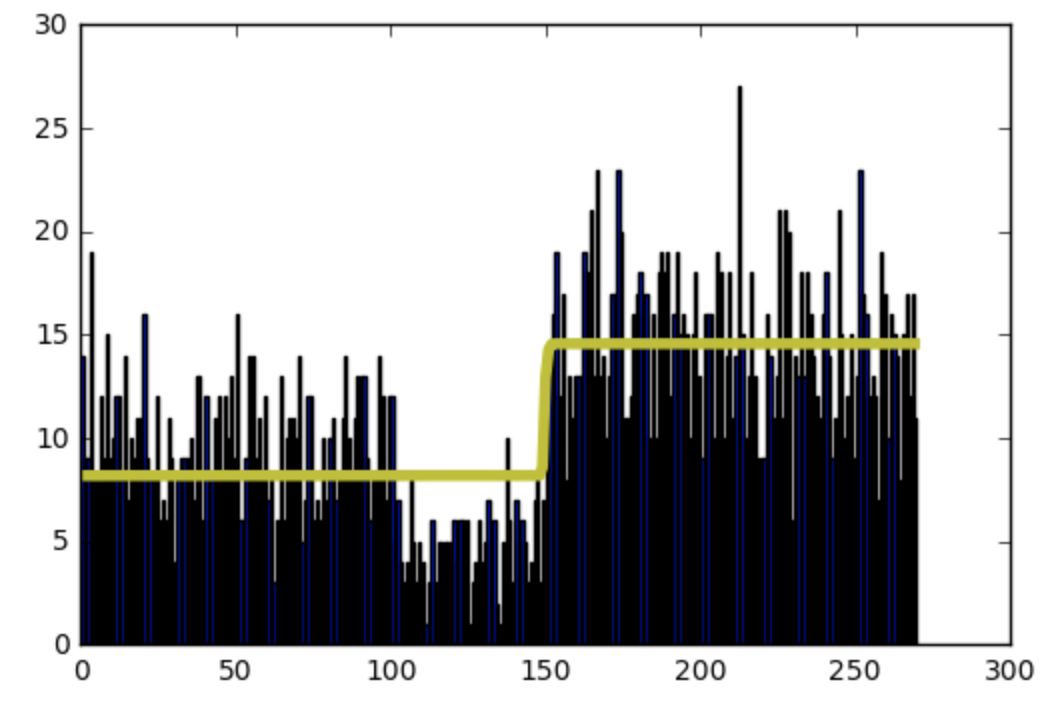
こんな感じですね
結果はというと、、、


確かに変化点が少ないので正しくは推定できていないものの
でも与えられた範囲内では問題なさそうです
シュミレーション値と推測値を合わせても、一つの変換点は間違っていないことがわかります
では変化点が多い場合はどうでしょう?
alpha = 1.0 / data.mean()
lambda_1 = pm.Exponential("lambda_1", alpha)
lambda_2 = pm.Exponential("lambda_2", alpha)
lambda_3 = pm.Exponential("lambda_3", alpha)
lambda_4 = pm.Exponential("lambda_4", alpha)
tau = pm.DiscreteUniform("tau", lower=0, upper=n-1)
tau_2 = pm.DiscreteUniform("tau_2", lower=0, upper=n)
tau_3 = pm.DiscreteUniform("tau_3", lower=0, upper=n)
@pm.deterministic
def lambda_(tau=tau, tau_2=tau_2, tau_3=tau_3, lambda_1=lambda_1, lambda_2=lambda_2, lambda_3=lambda_3, lambda_4=lambda_4):
out = np.zeros(n)
out[:tau] = lambda_1
out[tau:tau_2] = lambda_2
out[tau_2:tau_3] = lambda_3
out[tau_3:] = lambda_4
return out
observation = pm.Poisson("obs", lambda_, value=data, observed=True)
model = pm.Model([observation, lambda_1, lambda_2, lambda_3, lambda_4, tau, tau_2, tau_3])
さてさて結果です


いきなりのカオスですね、、、
変化点が多い場合はこれだけはっきりしたものでも推測がおかしくなることがわかります
まとめ
変化点の仮説が異なった場合の動きを簡単に検証して見ました
「じゃあ変化点はいくつがいいの?」という話がありますが、値をレトロスペクティブに評価するなら明らかに重なったような場合は点を減らした方がいいのかもしれません(まあモデルが間違っている場合の方が多いでしょうが、、、)
もしくは変化点の数も推定するモデルを描いてもいいかもですね