機械学習ではデータを$\mathbb{R}^n$の元として扱い,分類や回帰といったタスクを$\mathbb{R}^n$から$\mathbb{R}^m$への写像として構成します.
ところが近年Poincare Embedding等$\mathbb{R}^n$以外の世界で考えることによる効果がいくつか得られています.
今回調べた$p$-adicな構造もそうした実数ではありえない構造の一つです.
これは大学数学の知識を少し仮定して、$p$-adicな機械学習の現状を調べたものです.
調べた範囲だと2010年以降の論文はほとんどなかったので,改めてまとめておくだけでも価値があるかと思います.
数学の知識としては以下を仮定します.
- 位相空間論,特にコンパクト性や完備性
- 初等的な環論.例えば整域に対する商体の操作や環の乗法群の定義
とはいえ,なるべく丁寧に解説するので,定理の主張が読めれば特に問題ないかなとい思います.
Webで検索した範囲だとこれがわかっていれば問題ないかと思います.
そもそもp進とは
最初に$p$進という概念が整数論で使われている背景を説明します.
歴史的な正しさは保証しません.あくまでモチベーションとして理解していただけたらと思います.
その後$p$進整数環$\mathbb{Z}_p$とその商体$\mathbb{Q}_p$を実際に定義し,いくつかの性質を説明します.
$p$進という概念は整数論でよく使われます.
整数論ではある方程式の整数解や有理数解が存在するかが重要な問題になっています.
代表的な問題であるフェルマーの最終定理を紹介しましょう.
| Theorem(フェルマーの最終定理) |
|---|
| $n$が3以上の整数の時、$x^n+y^n=z^n$を満たす正の整数の組$(x,y,z)$は存在しない |
これが360年未解決であったことからも方程式が整数解を持つかどうかの判定が難しいことがわかると思います.
実際に具体例を通じてどういう難しさがあるかを見ていきます.
例1
よく知られているように実数には$\sqrt{2}$が存在します.
これは$x^2-2$が$x=0$の時-1.$x=2$の時2となり,中間値の定理から$x^2-2=0$となる方程式の解の存在が言えるからです.
ですが,有理数の場合は中間値の定理が成り立たないので、解の存在が簡単に示せません.
違う見方をすると
$1.4, 1.41, \ldots$と$x^2 -2$が0に近づくように点列を構成できれば,実数の完備性から存在を証明できます.
一方で有理数は完備でないので、どれだけ近いものが存在しても本当に存在するかはわかりません.
実際,$\sqrt{2}$にいくらでも近い有理数は存在しますが,$\sqrt{2}$は有理数ではありません.
例2
円の方程式$x^2 + y^2 = 1$を実数上と有理数上で考えます.
実数上ではもちろん有理数上でも無数の解を持ちます.
例えば$(x,y) = (\frac{1- t^2}{1 + t^2}, \frac{2t}{1 + t^2})$は$t$が有理数のとき有理数の組となり,$x^2 + y^2 = 1$となります.
この円の方程式の半径を大きくしてみます.
今回は$x^2 + y^2 = 3$が実数上と有理数上で解がどの程度あるか考えましょう.
実数の場合は無数に持つことはすぐわかります.では有理数上の場合はどうでしょうか.
実は有理数上では解を持ちません.証明してみましょう.
有理数解$(a/b,c/b)(b \neq 0)$が存在したと仮定します.
すると,整数の間の関係式$a^2 + c^2 = 3b^2$ができますが
左辺は3で偶数回割れるのに対し,右辺は3で奇数回割れ矛盾するので,有理数解を持たないことがわかります.
この例からは以下がわかります.
- 実数上の斉次多項式$=a$いう形の方程式は右辺を正の実数倍しても解の個数は変わらない.
- 有理数上では同様の条件でも解の個数が無限の場合も0の場合もあり,その挙動を特定する条件付けが"簡単に"はわからない.
もちろんこうした例だけではどんな方程式でも実数の場合より有理数の場合の方が難しいという一般的な結論は何も言えません.
ですが,どういう困難があるかつかめればと思い紹介しました.
$p$進数は上の例のような困難さを緩和する役割を持ちます.
実際$\mathbb{Q}_p$は完備ですし,以下のような定理が成り立ちます.
| Theorem(Hasse-Minkowskiの定理) |
|---|
| $a,b \in \mathbb{Q}^{\times}$に対し,以下は同値. $\bullet$ $X^2 - aY^2 - bZ^2 = 0$が$\mathbb{Q}$上で$(0,0,0)$以外に解を持つ. $\bullet$ 任意の素数$p$および$p=\infty$の時(つまり実数の時)に $X^2 - aY^2 - bZ^2 = 0$が$\mathbb{Q}_p$上で解を持つ. |
p進数の定義
実際に$p$進数の導入と定義をしていきます.
先程整数解を持つかどうかの判定はかなり難しいといいましたが,解がないの証明は簡単な場合もあります.
整数係数一変数多項式の方程式$f(x) = 0$が与えられたとします.
これが整数解を持つとしましょう.
すると,その方程式は全ての正の整数$n$に対し,$\mathrm{mod} \ p^n$でも解を持ちます.
もちろん逆に$\mathrm{mod} \ p^n$で解を持ったとしても整数解を持つとは限りませんが,
これは有限の世界で考えることになるので,しらみつぶし的に確認すれば解の存在有無は判定できます.
そして,ある$n$で$f(x) = 0$が解を持たない場合,整数でも解を持たないことが判定できるようになります.
ですが,実際に全ての$n$で解を持てば、整数解を持つのでしょうか?
| Question |
|---|
| 全ての$n$に対し$f(x)=0$が解を持つことは整数解を持つこととどのぐらい違うのだろうか? |
と自然に気になるわけです.違いを考えるためにも,全ての$\mathrm{mod} p^n$でうまくいくような数全体を定義します.
$$
\mathbb{Z}_p := \{(x_0,x_1, \ldots) \in \prod \mathbb{Z} / p^{n+1} \mid x_i \equiv x_{i-1} \mathrm{mod} \ p^i\}
$$
remark
位相環のイデアル$I$による完備化を知っている人向けにいうと,$\mathbb{Z}_p$は$\mathbb{Z}$の$(p)$進完備化となります.
remark
$p$は素数です.英語のPrime Numberからとってます.
記号からわかるかもしれませんが,これが$p$進整数環と呼ばれるものです.
定義から$\mathbb{Z}_p$上で一変数多項式の作る方程式が解を持つことは全ての$n$に対して解を持つことは同値になります.
証明しませんが$\mathbb{Z} \subset \mathbb{Z}_p$であり,$\mathbb{Z}_p \setminus \mathbb{Z}$は非加算無限集合となります.
なのである$p$を一つだけ考えても整数解を持つこととは大きく異なることがわかります.
話を$\mathbb{Z}_p$に戻しましょう.
定義から$\mathbb{Z}_p$の元は環の直積となりますが,無限和を使った表し方もあります.
$(x_0,x_1 \ldots ) \in \mathbb{Z}_p$に対し,
$\sum_{i=0}^{\infty} a_ip^i(0 \le a_i \le p)$を$\sum_{i=0}^ka_ip^i = x_k \mathrm{mod} \ p^{k+1}$となるように$a_i$を定めます.
これは$k$ごとに$a_i$の値が変わる定義ですが,実際にはどんな$k$でも同じ$a_i$を定めるので,well-definedな定義になります.
この時$(x_0,x_1 \ldots )$を$\sum_{i=0}^{\infty} a_ip^{i}$と表します.
今回は代数的な話は使わないので証明しませんが、以下の性質があります.
- $\mathbb{Z}_p$は単位元を持つ環になり,特に単項イデアル整域です.
- 単項イデアル整域では最大公約数や最小公倍数が定義でき,一般論ではイデアルを用いないと議論できないこと(≒元だけを見ても議論できないこと)が元での議論でこと足りることが多いです.
思い切って$\mathbb{Z}$と同じような扱いができる環だと思ってもよいかもしれません. - 整数の中で可逆元(かけたら1にできる数)は$1,-1$しかありませんが$\mathbb{Z}_p$では$p$で一度も割れない数全てが可逆元になります.
(無限和での議論に慣れていたら,一項目が可逆元であることと同値なことからすぐわかります) - $\mathbb{Z}_p$の任意の0でない元$x$はある可逆元$u$と0以上の整数$n$が存在し,$x = up^n$とかけます.
特に一番下の性質が重要です.
この性質のイメージは$p$進数は$p$で何回割れるかが重要で、それ以外はあまり考えないようにしたものと捉えることになるかもしれません.
ここからは$\mathbb{Q}_p$を作りましょう.
これは整数から有理数を作るのと同様の方法を使います.
つまり$a,b \in \mathbb{Z}_p, b \neq 0$とした時$a /b$とかける元全体で定義します.(厳密には商体なので、同値関係が入っています.)
$\mathbb{Z}_p$との違いを見てみると,
$\mathbb{Z}_p$の任意の0でない元$x$はある可逆元$u$と0以上の整数$n$が存在し,$x = up^n$とかけたことに対し,
$\mathbb{Q}_p$の任意の0でない元$x$はある$\mathbb{Z}_p$の可逆元$u$と整数$n$が存在し,$x = up^n$とかけることになります.
つまり$p$でマイナス回割れた対象も含めたものが$\mathbb{Q}_p$となります.
remark
位相を定める前ですが、重要なので余談として収束について述べてきます.
このようにかかれた全ての数がある$x$を定めるので、無限和としては収束します.
これは部分和を考えると$\sum_{i=0}^k a_ip^i$がコーシー列になるということを意味します.
なので、$a_ip^i$は$i$が大きくなるにつれ0に近づきます.
これは$a_i$のとり方には依存しない話なので$p$で割りきれる程$0$に近づくような位相を考えていることに注意してください.
(逆に$p$が$-\infty$方向に無数にあるような元は収束しません)
p進の特徴:付値
前節では$\mathbb{Q}_p$の定義を述べました.
ここでは$p$進の重要な性質である付値について述べます
| Definition |
|---|
| $v:\mathbb{Q}_p \to \mathbb{Z} \cup \infty$を$x \in \mathbb{Q}_p$に対し, $x=0$の時,$v(x) = \infty$, $x = p^m y(y \in \mathbb{Z}_p^{\times} )$とかけるため. $v(x) := m$と定める、これを $p$進付値 という. |
remark
付値は$\mathbb{Q}$でも定義できます.ですが,$p$進では付値が実質一つであり,さらに完備離散付値を定めていることが重要なポイントです.
付値の性質をみましょう
| Lemma |
|---|
| $p$進付値には以下の性質が成り立つ. 1. $v(x+y) \ge \mathrm{min}\{v(x), v(y) \}$ 2. $v(xy) = v(x) + v(y)$ |
| 簡単なので、実際に証明してみてください. |
| $p$で何回割れるかをみてるので,足し算や掛け算のあと何回割れるかを見てくれればいいかと思います. |
さらにこの付値は以下の強力な性質を満たします.
| Lemma |
|---|
| $v(x) > v(y)$の時,$v(x+y) = v(y)$となる |
これは今後も出てくるのでここで証明してみます.
$v(x) > v(y)$となることから,$\mathrm{min}\{v(x), v(y) \} = v(y)$となります.
よって上の補題の1.から
$v(x+y) \ge v(y)$となります.
一方で$y = x+y - x$となるので,
$v(-1) = 0$となることに注意すると,
$v(x+y) \ge v(x)$とすると
$v(x+y - x) \ge v(x)$となり,$v(x) > v(y)$に矛盾します.
よって$v(x+y) < v(x)$となり,上の補題の1.から
$v(y) \ge v(x+y)$となります.
これから$v(x+y)=v(y)$となります.
付値は単なる写像を定めるだけでなく距離を与えます.
| Propostion |
|---|
| $d(x,y) := p^{- v(x-y)}$とすると$\mathbb{Q}_p$は(完備)距離空間になる. |
付値の定める距離はは通常の距離の公理に加え
$d(x,y) \le \mathrm{max}\{d(x,z), d(z,x)\}$
となります.
こうした距離のことを ultrametric といいます.
ultrametricな距離空間では三角形は必ず二等辺三角形になります.
ここまでで$p$進数の導入を終わりたいと思います.$p$進数については
- $p$で何回割れるかに基づく付値が定義されている
- 付値を元に距離を定義でき,その距離はユークリッド距離とは異なる性質を持つ
ということがわかっていれば,次からも読めるかなと思います.
p-adic machine learningに興味をもったきっかけ
ここからは実際に機械学習でどう$p$-adicやultrametricが使われているか述べたいと思います.
僕がモチベーションをもったきっかけですがある論文で以下のような記載がありました.
In the work of [66, 67]
it was shown how as ambient dimensionality increased
distances became more and more ultrametric.
[66] R. Rammal, J.C. Angles d’Auriac, and B. Doucot. On the degree of ultrametricity. Le Journal de Physique – Lettres, 46:L–945–L–952, 1985.
[67] R. Rammal, G. Toulouse, and M.A. Virasoro. Ultrametricity for physicists.
Reviews of Modern Physics, 58:765–788, 1986.
これを読んで,高次元のデータになるにつれ,距離はよりultrametricになっていくのかと思いました.
そこで,[67]は無料では読めなかったので,無料で読めた66を読みました.
読んでみると,高次元のデータはultrametricに近づくという主張には全く読めませんでした.
特にこの論文での自分たちの貢献ポイントがほとんど理解できませんでした.
とはいえ、機械学習の論文でそういうことはよくありますし,ここで書いてあった内容を私の理解した範囲で紹介します.
まず考える問題を定義しましょう.
| Problem |
|---|
| $(\Omega,d)$を有限距離空間とします.この時$d$に一番"近い"ultrametic $d'$を求めたい. |
そもそも全ての距離を比較してどっちがに近いという言葉は定義できないので,問題を正確に定式化しましょう.
比較ができるように以下で距離に対する順序を定めます.
$$
d^{\prime} \leqslant d \Leftrightarrow d^{\prime}(x, y) \leqslant d(x, y) \quad \text { for all } \quad(x, y) \in \Omega \times \Omega
$$
$\mathbf{U}$ を $\Omega$ における ultrametric な距離全体とし、 $\mathbf{U}^{<}=\left\{d^{\prime} \in \mathbf{U} | d^{\prime} \leqslant d\right\}$で$d$以下のultrametric全体とします.
この定義からわかることを書きます.
| Lemma |
|---|
| $\mathbf{U}^{<}$は空集合でない. |
任意の異なる二点の距離は0ではなく,さらに$\Omega$は有限なので$d(x,y)$の最小値$a$は存在します.任意の異なる二点$x',y'$に対し,
$d'(x',y') = a$とすれば,それは定義からultrametricになり,順序も満たします.
よって少なくとも一つは条件を満たすultrametricが存在します.
| Lemma |
|---|
| $\mathbf{U}^{<}$は全順序集合とは限らない. |
例えば3点${a,b,c}$で
$d(a,b) = d(b,c) = d(a,c) =2$
$d_1(a,b) = 1, d_1(a,c) = 1, d_1(b,c) =1.5$,
$d'(a,b) = 1.5,d'(a,c) =1,d'(b,c)=1$はともにultrametricになり,
$d_1,d' \in \mathbf{U}^{<}$となりますが,これらは順序関係にありません.
$\mathbf{U}^{<}$は距離全体のなす集合と比べるとかなり少ない気がするのですが、
ここだけを考えれば十分なのかはよくわかりません.
(もちろん,この中にあるultrametricで十分近いものが存在すれば問題ないのですが...)
これを定義したのは,この順序に対する極大元$d^{<}$はただ一つ存在するからです.
一方で$d$以上の距離を持つultrametric全体の極小元はただ一つではなく,この設定のうまさを感じます.
$d^{<}$はdから以下のように構成的に距離を定めることができます.
$$
d^{<}(x, y)=\operatorname{Max}\left\{d\left(w_{i}, w_{i+1}\right), 1 \leqslant i \leqslant n-1\right\}
$$
ただし$w_i$は$\Omega$から誘導した距離で定義した無向グラフのminimal spanning tree上の($w_1 = x ,w_n = y)$となるパスです.
構成できることがわかればいいので,詳細は省略します.気になる人は元論文を読んでみてください.
それを subdominant of ultrametric といい,$d^<$で表します.
さらに、
$\Omega$上の2つの距離$d,d'$に対し,
$$
\Delta_{\infty}(d, d') = \mathrm{Max}_{(x,y) \in \Omega^2}\vert d(x,y) - d(x,y)\vert
$$
と
$$
\Delta_{a}(d, d^{\prime})=\left[\sum_{x, y \in \Omega}\left|d(x, y)-d^{\prime}(x, y)\right|^{a}\right]^{1 / \alpha}, \quad \alpha>0
$$
を定めます.
$d^<$は以下の性質を満たします.
| Propostion(Optimality) |
|---|
| $d^<$は$U^<$上で$\Delta_{\infty}(d, d')$ やより一般に$\Delta_{a}(d, d')$を最小にする唯一の距離である. |
| Propostion(stability) |
|---|
| $\lambda d$に対する subdominat of ultramericは $\lambda d^<$になる. |
こうした性質を満たすところからも定義はかなりうまいと思います.
ただ,この定義は全く空間の次元と関係ありません.$\Omega \subset \mathbb{Q}_p^n$だとしても$n$の値で特に何か変わるものがありません.つまり,距離さえ全て同じなら高次元だろうが,本質的に何も変わらないので,
この時点で高次元でもultrametricに近くなるかは次元ではなく,距離に依存していると気づくべきだったかもしれません.
そうすればただ高次元なのがいいのではなく,少なくともデータの分布に強い仮定が必要であると想像できたかなと思います.
ここからは特に怪しくなります.
この論文の貢献ポイントは
$$
\mathcal{D} = \frac{\sum_{x,y \in \Omega} (d(x,y) - d^<(x,y)) }{\sum_{x,y \in \Omega} d(x,y)}
$$
として,これでどのぐらいultrametricから離れているかを表す尺度と定義し、
この値を一般的に評価したことではなく,いくつかの例で評価したところのようです.
ただ,正直ほとんど何を言ってるかわからず,
- 実直線上の有限個の点集合点の個数を増やした極限では$\mathcal{D} = 1$となる.
- $\Omega = 2^B$に対しハミング距離で距離を定義した空間でも$\mathcal{D}$がどんどん増える
と読めました.
まとめるとこの論文からは以下のことが言えるんじゃないかと思います.
(僕の理解が間違っているなら本当に突っ込んでほしいものです.)
- ある距離に対して、それに比較的近いといえるultarmetricを構成できる
- とはいえ、その距離が元の距離とどの程度近いかはわからない.
- データに強い仮定を課した場合は解析が可能だが,いくつかの例では実際の距離と離れていくという結果だった.
- 空間の次元との関連は明には述べられていない.
- ultrametricを元の距離に基づいてとってくる話だったので、p-adicな距離空間に埋め込むとうまくいくかとは別の話.
なので,ユークリッド距離がp-adicな距離に近くなることは期待しない方がよさそうです.
機械学習アルゴリズム
悲しい結論に終わった背景的な話はここまでです.
これからは,実際の機械学習モデルの話に移りたいと思います.
機械学習ではモデルを作るわけですが,そのためには
- データ
- アルゴリズム
が何かを考える必要があると思います.
今からは都合のよいデータがあったとして,使えそうなアルゴリズムが実際にどういうものか考えます.
データの内在的な構造の依存した方法
$\mathbb{Q}_p$の有限部分集合$X$は特徴的な構造を持っています.
実は,距離を用いてrooted treeを構成することができます.
実際に$X$からrooted metric tree $D(X)$を求めるアルゴリズムを書きます.
treeの各nodeは$X$のある部分集合として作ることに注意してください.
構成方法
treeの末端全体を$X$の1点集合全体とします.
ここから一段ずつ上のnodeを構成していきます.
二点の距離の最小値を$\min\{d(x,y) \mid x,y \in X\}=p^{-k}$とします.
$B_n(x) = \{y \in X \mid d(x,y) \le p^{-n}\}$とします.
$k+1$から1に向かって順に以下を繰り返します.
- もし$\# B_n(x) > \# B_{n-1}(x)$となる時はを結び,$B_n(x)$をnodeとして追加し,その子ノードとして,node $B_{n}(x) \setminus B_{n-1}(x)$とnode $B_{n-1}(x)$とします.
これでrootは$X$になるrooted treeが作れます.
文章だけだとわかりづらいと思うので、例をあげて確認します.
例
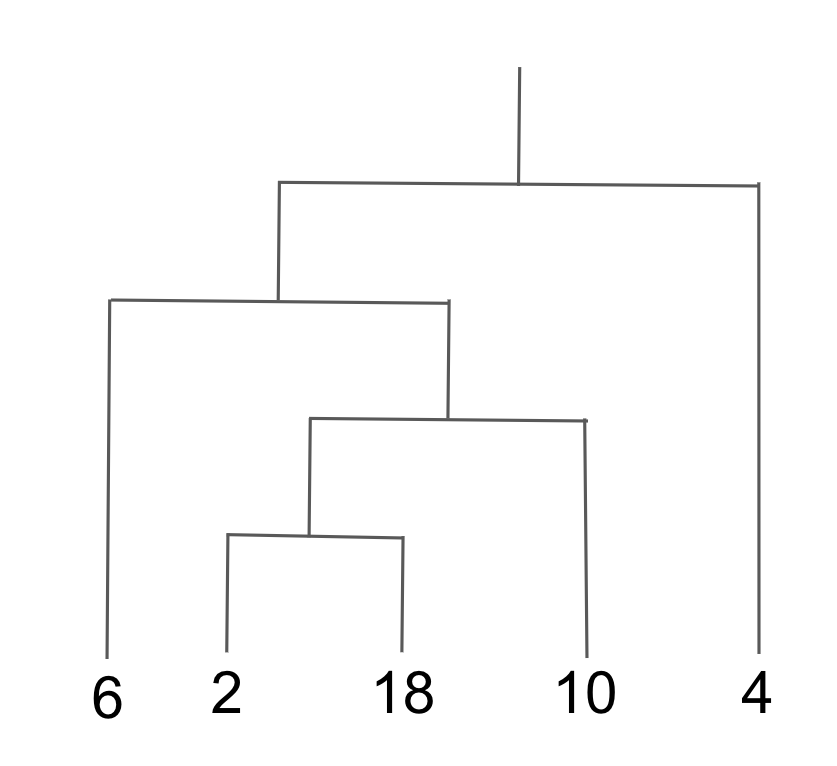
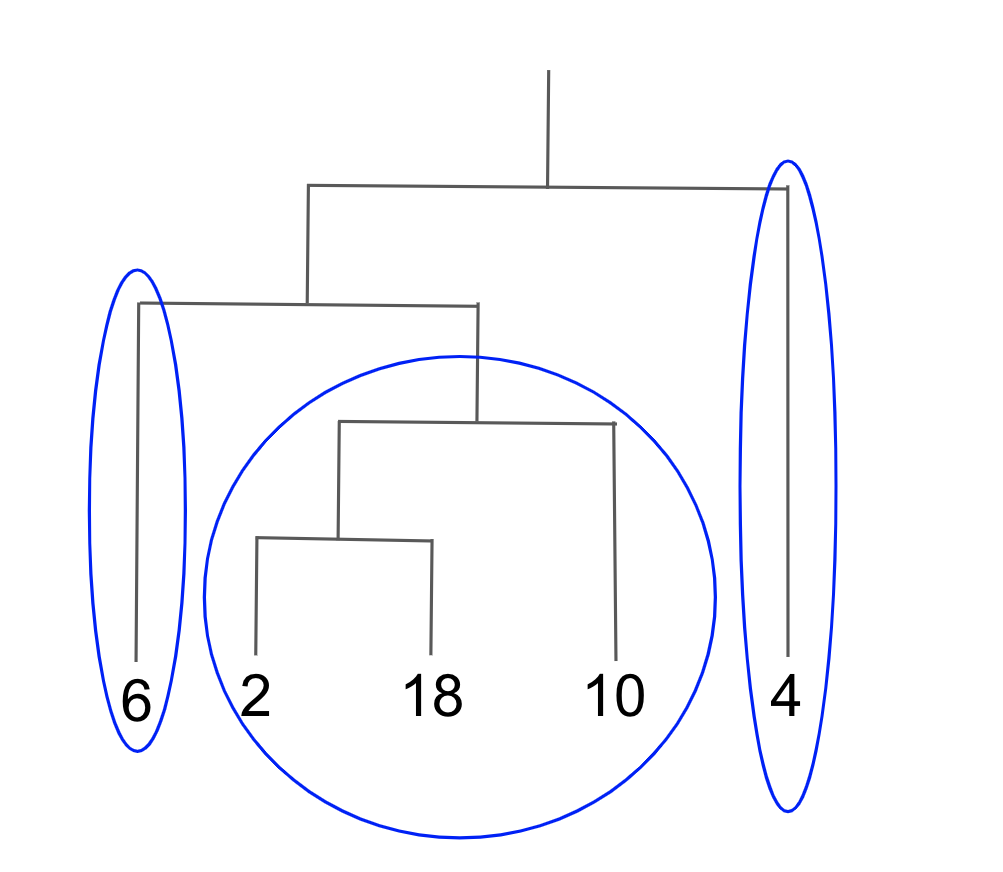
$X=\{2, 4, 6, 10, 18\}$としましょう.
$v_2(x)$を$x$が2で割れる回数とし,$d(x,y) = 2^{- v_2(x-y)}$とします.
すると距離の最小値が$(2,18)$の時の$1/2^4$となります.
そこから距離が$1/2^3,1/2^2,1/2$となるところを結んでいくと以下のようになります.
これがうまくいくのは以下が成り立つからです.
| Lemma |
|---|
| $y \in B_n(x)$に対し,$B_n(y) = B_n(x)$となる. |
もし$B_n(y) \setminus B_n(x) \neq \emptyset$とすると,
$z \in B_n(y) \setminus B_n(x)$が取れ,$d(x,z) > p^{-n}$となるわけですが,
$d(x,z) \le \max{d(x,y),d(y,z)} \le p^{-n}$より矛盾します.
なので親ノードを構成する時はその子ノード同士の適当な二点の距離だけを考えれば,問題ありません.
こうしたユークリッド空間の有限部分集合には存在しない階層構造が自然に定義できるのでこの構造を活かしくなります.
この構造は教師データを必要としないので,特にデータをクラスタリングすることが考えます.
数を指定して、適当にその数になるようにしてもいいかもしれませんが,
せっかくなので,機械学習でよく使われる損失関数を定義し,損失関数が最小となるようにクラスタリングをしましょう.
また新しい記号を定義します.
$v \in D(X)$に対し,$ch(v)$で$v$の一つ下のnode全体を表し,
$\mu(v) := \max \{d(x,y) \mid x,y \in v\}$とし,$v_0$でroot nodeを表します.
$V$を$D(X)$のノードのなす集合とします.
この時$V$に対する損失関数を
$$
E(V):= \sum_{v \in V} (\# v- 1) \mu(v)
$$
とします.
$\{v_1, \ldots, v_m\} =V$の時,$E(v_1, \ldots, v_m)$と表します.
すぐわかるように$E(ch(v)) \le E(v)$となります.
損失関数を定義したので考える問題を定義しましょう.
問題
$k$個以内のデータを分割したとして$E(V)$が最小となる分割を求めよ.
これを求めるアルゴリズムには以下のようなものがあります
- $ch(v_0)$の個数が$k$より大きい場合は分割しない.
- その後は$ch(v_0)$に従い,分割する.後は分割した後のクラスタ数が$k$未満となる極大の分割を全て求める.
- 分割に基づき$E(V)$を求め,その最小値を与える分割を与える.
要はクラスタ数が$k$を超えない範囲で可能な限り子ノードで分割するということです.
全探索しなくてもうまく枝刈りできる気もしたのですが,間違っているのはあれだと思ったので,全探索的に記述しています.
今までは学習アルゴリズムについてでした.推論の場合はどうなるでしょうか?
これもかなり単純で
未知のデータに対しても,各クラスタに属する$X$の要素どれかとの距離を求めればよいです.
そうると,どのクラスタに当てはまるかは判別できます.
On p-adic classficationでは中心も求めていましたが,今回のクラスタリングでは,内部の点ならどれでも問題ないと思うので,一旦ここまでにしておきます.
上の論文では、こうした分割の仕方を正解データを元にする教師あり学習の方法や
$p$を変えたらどうなるかも述べられていました.
$p$を変えてた場合には以下の結果が述べてあります.
| Theorem |
|---|
| $k$を定めれば有限個の素数を除き$X$のクラスに属する要素は同じになる. |
有限個の素数を除いて◯◯というタイプの定理です.
整数論ではままあるタイプの命題で,例えばAx-Kochen-Ershovの定理なども同じように述べられます.
この手の定理は素数に対する極限を調べることにより,十分大きい素数であれば◯◯であるという証明になりがちです.
なので,実際にどんな素数なら大丈夫でないかはわからないという課題があります.
さらに今回の場合は$X \subset \mathbb{Q}$と考えているので
非常に大きい素数を取ると,
例えば$X$の全てのを互いに素な形$x_i = a_i/b_i$で表した時に$\prod a_ib_i$より大きい素数を取ると,
二点の距離が割り切れず,全ての二点の距離が1となります.
なので,この場合,全てを一つずつに分割するか,全てをひとまとめにするかしかなくなります.
これは機械学習を使う側としては困る結果となってしまいました.
とはいえ数学的には面白いですし、クラスタリングが自明なものしかならないという結果が論文として普通に公開されているという事実も重要かなと思ったので記載しました.
p-adic Neural Network
さっきまではデータ自体の持つ階層構造を軸にした手法でした.
今度は教師データを中心としたアルゴリズムとして
$p$-adic Neural Networkの方法について述べたいと思います.
まずNeural Networkと呼ばれるものが,どういう関数を考えているかを説明し,
その後にパラメータの調整方法について説明します.
Neural Networkを表す関数$NN:\mathbb{Z}_2^N \to \{0,1\}^N$は以下のように構成されます.
$w_i \in \mathbb{Z}_2^N,f:\mathbb{Z}_2 \to {0,1}, x \mapsto 1 - I_{B_{\epsilon_k}}(0)(x)$とした時.
$$
NN(x) = (f(w_1 \cdot x), \ldots ,f(w_N \cdot x))
$$
で定めます.
ただし,$I_{B_{\epsilon_k}}(0)(x)$は$x \in B_{\epsilon_k}(0)$つまり$d(x,0) \le ϵ_k$なら,1を取り,それ以外の場合は0となる写像です.
また,$ϵ_k = 2^{-k}$とします.
remark
今の定義では$(w_i)$という行列をは一つかけたことになります.
一般のNeural Network,特に深層学習では行列を一つではなく複数かけることになります.
ただ今回はわかりやすさのために行列を一つとしました.
データセットを$\{x^{\alpha} = (x^{\alpha}_1, \ldots, x^{\alpha}_{N}), y^{\alpha} = (y^{\alpha}_1, \ldots, y^{\alpha}_{N})\}_{\alpha=1}^m$としましょう.
ただし,$x^{\alpha}_i \in \mathbb{Z}_2, y^{\alpha}_{i} \in {0,1}$です.
Neural Networkでは
$NN:\mathbb{Z}_2^N \to \{0,1\}^N$を損失関数が最小となるようにパラメータ$w = (w_1, \ldots, w_N)$を定めます.
まず損失関数を定義しましょう.
$$
\mathcal{L}\left(w ; x^{(\alpha)}, y^{(\alpha)}\right)=\frac{1}{m} \sum_{\alpha=1}^{m} \sum_{j=1}^{N}\left|y_{j}^{(\alpha)}-f\left(w_{j} \cdot x^{(\alpha)}\right)\right|
$$
とします.これが最小となるような$w$を求めることが今回やることです.
ただ、一旦は損失関数の話をおいておいて,まず特定の$x^{\alpha}$の時どうなっているかを考えます.
ここからは$x^{\alpha}$を固定して,そのときにどういう$w$なら大丈夫かを考えていることに注意してください.
$x^{\alpha} \in \mathbb{Z}_2^N$で$w \in \mathbb{Z}_2^N$に対し,$X_{\alpha}(w) = \sum w_i x_i^{\alpha}$によって$w$からの写像$X_{\alpha}$を定義できます.
もし,$y^{\alpha} \in 0$の時$V_{\alpha} = U_{ϵ_k}(0)$とし,逆に$y_{\alpha} = 1$のときは$U_{ϵ_k}(0)$の補集合とします.
$W_a:= X_a^{-1}(V_a)$とします.
$y$だけ一次元の状態、つまり$\{0,1\}$の元だとすると,
$x,y$に対し,$w$は$W_a$の元であれば正しく予測できることを言っています.
$W_a$の元といっても無数にあるので,その中でアルゴリズミックにとりやすいところを考えていきます.
ultrametricの場合は不等式の議論を同様にすることで以下が成り立ちます.
| Lemma |
|---|
| $w \in W_{\alpha}$の時, $B_r^N(w) \subset W_{\alpha}$ |
つまり$w$を一つ見つければ,その近くのものは条件を満たします.
さらに$\mathbb{Z}_2$がコンパクトで$U_{ϵ_k}(0)$は閉集合となります.
$\mathbb{Z}_2$では距離が離散的な値を取るので、半径を$\epsilon_k$未満で$\epsilon_{k+1}$より大きい値$\kappa$での開球となります.なので$U_{ϵ_k}(0)$は開集合かつ閉集合となります.
これから,$V_{\alpha},W_{\alpha}$は閉であり,特にコンパクトになります.
よって
$$
W_{\alpha}=\cup_{j=1}^{s_{\alpha}} B_{\epsilon_{k}}^{N}\left(w^{j}\right), B_{\epsilon_{k}}^{N}\left(w^{j}\right) \cap B_{\epsilon_{k}}^{N}\left(w^{i}\right)=\emptyset, i \neq j
$$
となる$w_j$を取れます.
$$
w_{l}^{j}=\sum_{n=0}^{\infty} \beta_{l n}^{j} 2^{n}, \beta_{l n}^{j}=0,1
$$
と無限和で表します.
この時,
$\left[w_{l}^{j}\right]_{k}=\sum_{n=0}^{k-1} \beta_{l n}^{j} 2^{n}$とします.
そうすると,ultrametricの議論から$B_{\epsilon_{k}}\left(w_{l}^{j}\right)=B_{\epsilon_{k}}\left(\left[w_{l}^{j}\right]_{k}\right)$となります.
よって
$$
\mathbf{N}_{k}=\left\{n=\sum_{l=0}^{k-1} \beta_{l} 2^{l}, \beta_{l}=0,1\right\}
$$
の中で$w_i^j$を考えればよいです.
ようやく損失関数の話に戻ります.この時,損失関数$E$を最小にする$w$
とは可能な限り多くのデータに対し,$w_i \in W_{\alpha}$となるもののことになります.(添字を省略しましたが,察してください.)
少なくとも有限個なので,全探索で計算すれば求められます.
これを減らす方法はいくつかありますが,- Learning of p-adic neural networksでは乱数を使いヒューリスティックな方法を提唱しています.
これでひとまず,基本的な学習モデルを2つ紹介しました.
これらと独立な手法というのは見当たりませんでしたが,Degenerateing familes of dendrogramsではベルコビッチ空間を使い階層的なクラスタリング手法を高度化できると言っています.
ですが,私には負えなかったので,今後のお楽しみとさせてください.
データ
今まではアルゴリズムの話を中心にしていましたが,$p$-adicだと思うとやりやすいデータの例をあげたいと思います.
実際こうしたデータがかなり少ないため$p$-adi machine learningが盛り上がっていないような気がしています.
明らかにうまくいきそうなデータは思い浮かばないので,まず明らかにうまくいかないデータを考えます.
それは実数であることを使うデータ,例えば身長や体重のような"連続的"なものです.
こうしたデータの場合は大小の構造が消えますし$p$-adicな世界では測定誤差で距離が大きく変わることになるので,現実的ではないでしょう.
実際に紹介されていた例をみます.
-
p-Adic Structure of the Genetic Code
では遺伝子を$p$進のデータと考えています.
GATCを0,1,2,3とみなし,遺伝子を5進の列で表して考えています.
この論文は機械学習的な内容はありませんが,データの典型的な例として紹介しました.
他にもImage Segmentation with the Aid of the p-Adic MetricsではSegmentationをp進を使って実現しているようでした,ここから少し見れますが実際はよくわかりません.
こうしたデータをみても離散的なおかつ,ある程度複数にまたがるようなものがいい気がしますね.
まとめ
ここまでの内容を改めて整理してみました.
- $p$-adicなデータはtree構造を持つので,それに基づくクラスタリングが可能
- tree構造を使わない教師あり学習として,$p$-adic Neural Networkがある.
- $p$-adicが有効活用しやすいデータは遺伝子等数少ないのが現状
今回調べた限りまだまだわからない問題が多いなという感想です.
特に以下ができるといいのではないかと思います.
- $p$-adicな空間に埋め込むのが自然なデータの新たな例
- 普遍近似性定理等の関数に対する理論的な限界値
- backpropagation相当の汎用的なパラメータチューニング手法
- 評価データに対する誤差や汎化誤差
理論的な話を考える場合について現状思っていることを述べておきます.
これらを考える場合は連続関数全体やexp,log,微分,積分等を考える必要があるのかなと思います.
連続関数はMahlerの定理からかなり具体的にわかっているので,意外と簡単かもしれません.
逆に$\mathrm{exp},\mathrm{log}$を使った議論はむずかしいと予測しています.
というのも$\mathrm{exp}$の収束半径が無限大でないため,値によっては収束しません.
また,$\mathrm{log}$も$\mathbb{C}$と同じように値が一つに定まらないという現象が起きます.
こうした実数のときには起きない問題に対処するためによりシビアな議論が要求されるのではないかと思います.
とはいえ,不可能だとわかってるわけでもありませんし,こうしたものを整理しつつ,
$p$-adicな機械学習が活用できればなあと思っています.
なので,もし内容に興味があったり,疑問があればどしどしtwitte
rまで連絡ください.
参考文献
今回のものを書くために読んだもの一覧(URLとタイトルのみ)
論文
- Degenerateing familes of dendrograms
- Hierarchical Clustering for Finding Symmetries and Other Patterns in Massive, High Dimensional
- Image Segmentation with the Aid of the p-Adic Metrics
- Learning of p-adic neural networks
- On p-adic classfication
- On the degree of ultrametricity
- p-Adic Structure of the Genetic Code
- Trees and ultrametric spaces: a categorical equivalence
- Ultrametric Component Analysis with Application to Analysis of Text and of Emotion
- Ultrametricity increases the predictability of cultural dynamics
書籍