はじめに
以前『pythonでSVM実装』でハードマージンSVMについてまとめました.
前回,制約条件を罰金項に加えることで最適化しましたが,今回アクティブセット法という手法を使って最適化しました.
教科書として『サポートベクトルマシン』を使いました.
本記事の構成
- はじめに
- ソフトマージンSVM
- 主問題
- 双対問題
- アクティブセット法
- pythonでの実装
- 結果
- おわりに
ソフトマージンSVM
SVMの導入については『pythonでSVM実装』を参照してください.
マージン最大化,ラグランジュ未定乗数法,KKT条件について説明してあります.
主問題
ソフトマージンSVMでは,非負の変数 $\xi_i \geq 0, i \in [n]$ を導入し,制約条件を以下のように定義します.
y_i(\boldsymbol w^T \boldsymbol x_i + b) \geq 1 - \xi_i, \ \ i \in [n]
$\xi_{i}$ によりマージンは $1$ より小さくなり,$\boldsymbol x_i$ がマージンを超えて異なるクラス側に入ってくることを許容します.
誤分類が発生した場合,$\xi_{i} > 1$ となるため $\sum_{i \in [n]} \xi_{i}$ がある整数 $K$ 以下であれば,誤分類の数も $K$ 以下となります.
このことから,$\sum_{i \in [n]} \xi_{i}$ をなるべく小さくすることで誤分類を抑制できることがわかります.
以上を踏まえて,ソフトマージンSVMの主問題を以下のように定義します.
\begin{align}
& \min_{\boldsymbol w, b, \boldsymbol \xi} \frac{1}{2}\|\boldsymbol w\|^2 + C\sum_{i \in [n]} \xi_{i} \\
& \\
& s.t. \ \ y_i(\boldsymbol w^T \boldsymbol x_i + b) \geq 1 - \xi_i, \ \ i \in [n] \\
& \\
& \ \ \ \ \ \ \ \ \xi_{i} \geq 0, \ \ i \in [n]
\end{align}
係数 $C$ は正則化係数と呼ばれる正の定数です.
目的関数の第1項はマージン最大化の意味を持ちます.
第2項は元の制約条件 $\boldsymbol w^T \boldsymbol x_i + b \geq 1$ に対する違反の度合い $\xi_{i}$ がなるべく小さくなるよう抑制します.
正則化係数 $C$ は,この抑制の度合いを調節するためのパラメータとなります.
$C$ を大きくするとハードマージンに近づき,$C = \infty$ では,$\boldsymbol \xi$ の要素が値を持つと目的関数に無限の値が加算されるため,$\boldsymbol \xi$ は常に $\boldsymbol 0$ となります.
逆に $C$ を小さくすると誤分類を許容するようになります.
双対問題
では,主問題を双対表現することを考えます.
ラグランジュ未定乗数 $\alpha_i \geq 0, \ \ i \in [n]$ および $\mu_i \geq 0, \ \ i \in [n]$ を導入します.
ラグランジュ関数は以下のように定義されます.
L(\boldsymbol w, b, \boldsymbol \xi, \boldsymbol \alpha, \boldsymbol \mu)
= \frac{1}{2}\|\boldsymbol w\|^2 + C\sum_{i \in [n]} \xi_{i} - \sum_{i \in [n]} \alpha_i(y_i(\boldsymbol w^T \boldsymbol x_i + b) - 1 + \xi_i) - \sum_{i \in [n]} \mu_i \xi_i \tag{1}
$L$ の $\boldsymbol w, b, \boldsymbol \xi$ での偏微分は $0$ となります.
\begin{align}
& \frac{\partial L}{\partial \boldsymbol w} = \boldsymbol w - \sum_{i \in [n]}\alpha_{i}y_i{\boldsymbol{x}}_i = \boldsymbol 0 \tag{2} \\
& \\
& \frac{\partial L}{\partial b} = \sum_{i \in [n]}\alpha_{i}y_i = 0 \tag{3} \\
& \\
& \frac{\partial L}{\partial \xi_i} = C - \alpha_i - \mu_i = 0 \tag{4} \\
\end{align}
式(1)に式(2), (3), (4)を代入して整理すると以下のようになります.
L = -\frac{1}{2} \sum_{i, \ j \in [n]}\alpha_{i}\alpha_{j}y_{i}y_{j}{\boldsymbol{x}_i}^T\boldsymbol x_j + \sum_{i \in [n]}\alpha_i \tag{5}
制約条件である式(3), (4)および $\xi_i \geq 0$ と式(5)をまとめると双対問題は以下のように表現できます.
\begin{align}
& \max_{\boldsymbol \alpha} -\frac{1}{2} \sum_{i, \ j \in [n]}\alpha_{i}\alpha_{j}y_{i}y_{j}{\boldsymbol{x}_i}^T\boldsymbol x_j + \sum_{i \in [n]}\alpha_i \\
& \\
& s.t. \ \ \sum_{i \in [n]}\alpha_{i}y_i = 0 \\
& \\
& \ \ \ \ \ \ \ \ \ 0 \leq \alpha_i \leq C, \ \ i \in [n]
\end{align}
最後に $y_{i}y_{j}{\boldsymbol x_i}^T\boldsymbol x_j$ を $i, j$ 要素に持つ行列を $\boldsymbol Q \in \mathbb{R}^{n \times n}$ として定義すると,双対問題はベクトル表記できます.
\begin{align}
& \max_{\boldsymbol \alpha} -\frac{1}{2} \boldsymbol \alpha^T\boldsymbol{Q\alpha} + \boldsymbol 1^T \boldsymbol \alpha \tag{6} \\
& \\
& s.t. \ \ \boldsymbol y^T \boldsymbol \alpha = 0 \tag{7} \\
& \\
& \ \ \ \ \ \ \ \ \boldsymbol 0 \leq \boldsymbol \alpha \leq C \boldsymbol 1 \tag{8}
\end{align}
アクティブセット法
制約条件式(7), (8)の下で目的関数の最大化を図ります.
今回制約付き最適化問題の標準的な解法としてアクティブセット法を使います.
ソフトマージンSVMの制約条件に対して,$\alpha_i = 0$ もしくは $\alpha_i = C$ となるような $i$ の集合をアクティブセットと呼びます.
双対変数の不等式制約の状態に応じて3つの集合を以下のように定義します.
\begin{align}
& O = \bigl\{ \ i \in [n] \ \ | \ \ \alpha_i = 0 \ \bigr\} \\
& M = \bigl\{ \ i \in [n] \ \ | \ \ 0 < \alpha_i < C \ \bigr\} \\
& I = \bigl\{ \ i \in [n] \ \ | \ \ \alpha_i = C \ \bigr\}
\end{align}
各事例がどの集合に属するかがわかっているならば,$\alpha_i = 0, \ \ i \in O$ および $\alpha_i = C, \ \ i \in I$ であるため,
$i \in M$ のみについて双対問題を解けばよいこととなります.
集合 $M$ に関する双対問題は以下のようになります(導出過程は省きます).
\begin{align}
& \max_{\boldsymbol \alpha_M} -\frac{1}{2} {\boldsymbol \alpha}_M^T{\boldsymbol Q}_M \boldsymbol \alpha_M^{ \ } - C \boldsymbol 1^T {\boldsymbol Q}_{I, M} \boldsymbol \alpha_M^{ \ } + \boldsymbol 1^T \boldsymbol \alpha_M^{ \ }
& \\
& s.t. \boldsymbol y_M^T \boldsymbol \alpha_M^{ \ } = -C \boldsymbol 1^T \boldsymbol y_I^{ \ }
\end{align}
この問題に対してさらに新たな双対変数を $\nu$ を導入して,以下のラグランジュ関数を得ます.
L = -\frac{1}{2} {\boldsymbol \alpha}_M^T{\boldsymbol Q}_M \boldsymbol \alpha_M^{ \ } - C \boldsymbol 1^T {\boldsymbol Q}_{I, M} \boldsymbol \alpha_M^{ \ } + \boldsymbol 1^T \boldsymbol \alpha_M^{ \ } - \nu \left(\boldsymbol y_M^T \boldsymbol \alpha_M^{ \ } + C \boldsymbol 1^T \boldsymbol y_I^{ \ }\right)
$\boldsymbol \alpha_M^{ \ }$ に関する微分を $\boldsymbol 0$ とおき,等式制約条件と合わせて整理すると以下の線形方程式に帰着できます.
\begin{bmatrix}
\boldsymbol Q_M & \boldsymbol y_M^{ \ } \\
\boldsymbol y_M^T & 0
\end{bmatrix}
\begin{bmatrix}
\boldsymbol \alpha_M^{ \ } \\
\nu
\end{bmatrix} = -C
\begin{bmatrix}
\boldsymbol Q_{M, I} \boldsymbol 1 \\
\boldsymbol 1^T \boldsymbol y_I^{ \ }
\end{bmatrix} +
\begin{bmatrix}
\boldsymbol 1 \\
0
\end{bmatrix} \tag{9}
$\nu$ はマージン上の点を $M$ としたときのバイアス $b$ を表しています.
つまり,最適な $\boldsymbol \alpha_M^{ \ }$ が得られたときの $\nu$ は最適なバイアス $b$ となります.
集合 ${O, M, I}$ を事前に知ることはできないため,アクティブセット法では,適当な初期値を与えて式(9)を解き,アクティブセットを更新します.
最後にアクティブセット法による最適化のアルゴリズムを示します.
- 入力:訓練データ $(\boldsymbol X, \boldsymbol Y)$
- 出力:双対問題の最適解 $\boldsymbol \alpha,$ バイアス $b$
- 初期化: $\boldsymbol \alpha \leftarrow \boldsymbol 0, \ \ I \leftarrow \phi, \ \ M \leftarrow \phi, \ \ O \leftarrow [n]$
- while $\ y_{i} \ f(\boldsymbol x_i) < 1, \ \ i \in O$ または $y_{i} \ f(\boldsymbol x_i) > 1, \ \ i \in I$ である $i$ が存在 do
- $I$ または $O$ から $M$ への移動
if $\left|1 - y_{i_O} \ f(\boldsymbol x_{i_O}) \right| \geq \left|1 - y_{i_I} \ f(\boldsymbol x_{i_I}) \right|$ または $I = \phi$
$\ \ \ M \leftarrow M \cup i_O, O \leftarrow O \backslash i_O$
if $\left|1 - y_{i_O} \ f(\boldsymbol x_{i_O}) \right| < \left|1 - y_{i_I} \ f(\boldsymbol x_{i_I}) \right|$ または $O = \phi$
$\ \ \ M \leftarrow M \cup i_I, I \leftarrow I \backslash i_I$
ただし,$i_O = argmax_{i \in O} -y_i \ f(\boldsymbol x_i), \ \ i_I = argmax_{i \in I} \ y_i \ f(\boldsymbol x_i)$ - repeat
- 線形方程式(9)の解を $\boldsymbol \alpha_M^{new}$ に代入
- $\boldsymbol d \leftarrow \boldsymbol \alpha_M^{new} - \boldsymbol \alpha_M^{ \ }$
- $\boldsymbol \alpha_M^{ \ } \in [0, C]^{|M|}$ の領域内で最大のステップ幅 $\eta \geq 0$ によって$\boldsymbol \alpha_M^{ \ } \leftarrow \boldsymbol \alpha_M^{ \ } + \eta \boldsymbol d$ とし,
制約条件の境界にぶつかった $i$ が存在する場合には $M$ から $I$ または $O$ へ移動 - until $( \ \boldsymbol \alpha_M^{ \ } = \boldsymbol \alpha_M^{new} \ )$
- end while
アクティブセット法によるソフトマージンSVMの最適化では,
$I$ または $O$ のデータの中で最も違反しているものを $M$ に加え,その状態での $\boldsymbol \alpha_M^{ \ }$ を求めます.
$I$ または $O$ と $M$ の間でデータを移動し,違反したデータがなくなったとき学習終了となります.
pythonでの実装
以下のように実装しました(コード汚くて申し訳ありません).
学習が収束しない場合があるので,アルゴリズムを間違って理解しているか,実装にミスがあるかもしれません.
自分で直せないので心優しい方デバッグお願いします(土下座).
import numpy
from matplotlib import pyplot
import sys
def f(x, y):
return y - x
def g(T, X, w, b):
return T * (X.dot(w) + b)
def argmax(T, X, w, b, li):
return numpy.argmax(g(T[li], X[li], w, b))
def solver(T, X, C, li, lm):
Ti, Tm = T[li], T[lm]
Xi, Xm = X[li], X[lm]
Qm = (Tm.reshape(-1, 1) * Xm).dot(Xm.T * Tm)
Qmi = (Tm.reshape(-1, 1) * Xm).dot(Xi.T * Ti)
A = numpy.vstack((numpy.hstack((Qm, Tm.reshape(-1, 1))), numpy.hstack((Tm, 0))))
B = -C * numpy.vstack((Qmi.sum(axis = 1).reshape(-1, 1), Ti.sum()))
B[:-1] += 1
return numpy.linalg.inv(A).dot(B)
def calc_eta(d, alpha):
index = (d != 0) * (alpha[lm] >= 0) * (alpha[lm] <= C)
eta_z = (0 - alpha[lm][index]) / d[index]
eta_c = (C - alpha[lm][index]) / d[index]
return numpy.hstack((eta_z[eta_z > 0], eta_c[eta_c > 0]))
def set_to_list(_set):
return list(_set)
def move(_from, _to, value):
_from.remove(value)
_to.add(value)
def graph(T, X, w, param):
seq = numpy.arange(-5, 5, 0.02)
pyplot.figure(figsize = (6, 6))
pyplot.xlim(-3, 3)
pyplot.ylim(-3, 3)
pyplot.plot(seq, -(w[0] * seq + b) / w[1], 'k-')
pyplot.plot(X[T == 1, 0], X[T == 1, 1], 'ro')
pyplot.plot(X[T == -1, 0], X[T == -1, 1], 'b^')
if '-s' in param:
pyplot.savefig('graph.png')
if '-d' in param:
pyplot.show()
if __name__ == '__main__':
param = sys.argv
numpy.random.seed()
N = 20
dim = 2
X = numpy.random.randn(N, dim)
T = numpy.array([1 if f(x, y) > 0 else - 1 for x, y in X])
X[T == 1, 1] += 0.5
X[T == -1, 1] -= 0.5
# initialize
alpha = numpy.zeros(N)
w = numpy.zeros(dim)
b = 0
C = 0.1
I, M, O = set(), set(), set(range(N))
li, lm, lo = set_to_list(I), set_to_list(M), set_to_list(O)
while numpy.argwhere(g(T[lo], X[lo], w, b) < 1).size > 0 or numpy.argwhere(g(T[li], X[li], w, b) > 1).size > 0:
flag = 0
if I == set():
io = argmax(-1 * T, X, w, b, lo)
move(O, M, lo[io])
flag = 1
if O == set():
ii = argmax(T, X, w, b, li)
move(I, M, li[ii])
flag = 1
if flag == 0:
io = argmax(-1 * T, X, w, b, lo)
ii = argmax(T, X, w, b, li)
if abs(1 - g(T[lo[io]], X[lo[io]], w, b)) >= abs(1 - g(T[li[ii]], X[li[ii]], w, b)):
move(O, M, lo[io])
else:
move(I, M, li[ii])
while M != set():
li, lm, lo = set_to_list(I), set_to_list(M), set_to_list(O)
solve = solver(T, X, C, li, lm)
alpha_new = solve[:-1, 0]
if numpy.array_equal(alpha[lm], alpha_new):
break
if alpha_new[(alpha_new < 0) + (alpha_new > C)].size == 0:
alpha[lm] = alpha_new
else:
d = alpha_new - alpha[lm]
eta = calc_eta(d, alpha)
if eta.size == 0 or d[d != 0].sum() == 0:
break
alpha[lm] += eta.min() * d
for i in numpy.argwhere(alpha[lm] <= 0)[:, 0]:
move(M, O, lm[i])
for j in numpy.argwhere(alpha[lm] >= C)[:, 0]:
move(M, I, lm[j])
w = ((alpha * T).reshape(-1, 1) * X).sum(axis = 0)
b = solve[-1, 0]
li, lm, lo = set_to_list(I), set_to_list(M), set_to_list(O)
if '-d' in param or '-s' in param:
graph(T, X, w, param)
結果
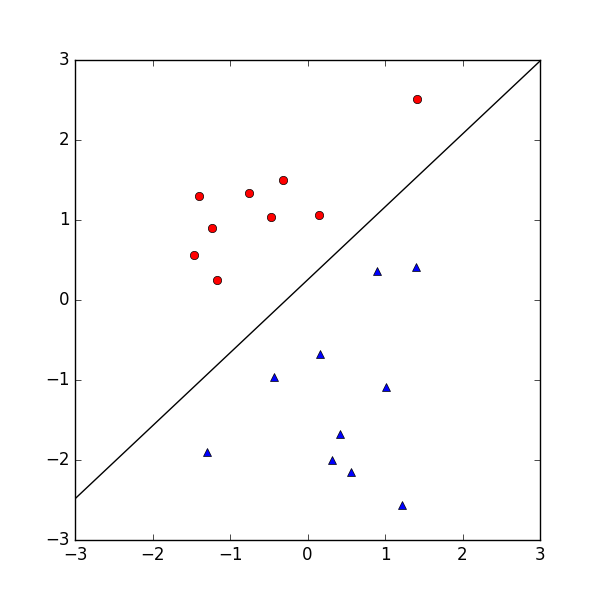
学習した $\boldsymbol w$ を使って直線を描画し,結果を画像として保存しました.
以下に結果を示します.
おわりに
アクティブセット法を使った双対問題の最適化ができました.
実装コードに誤りがある可能性が高いので,注意してください.