ポラード・ロー素因数分解法について

はじめに

本記事では表題のとおり、ポラード・ロー素因数分解法（Pollard's rho algorithm）という高速な素因数分解アルゴリズムについて紹介します。

ナイーブな実装としては自然数 $n$ に対して $2$ 以上 $\sqrt n$ 以下の整数で順番に試し割りして、割り切れるだけ割るといった $O(\sqrt n)$ のアルゴリズムがあります。
これに対してポラード・ロー素因数分解法では $O(n^{1/4})$ で $50$ ％以上の確率で素因数を発見することができます。¹

ポラード・ロー素因数分解法は簡単に述べると、与えられた自然数 $n$ が素数かどうか判断し、素数であれば終了、合成数であれば $n$ の約数を探し、またその約数が素数であれば素因数として出力に追加、合成数であればさらにその数に対して再帰的に約数の探索をするということを繰り返すアルゴリズムです。

$n$ 自身、また $n$ の約数が素数であるかどうかの判断には ミラー・ラビン素数判定法（Miller–Rabin primality test） を、約数の探索には フロイドの循環検出法（Floyd's cycle-finding algorithm） もしくは ブレントの循環検出法（Brent's cycle detection algorithm） に基づく約数探索手法をそれぞれ用います。

それぞれについて述べていきます。

目次

1. ミラー・ラビン素数判定法
2. フロイドの循環検出法に基づく約数の探索
3. リチャード・ブレントによる変形
4. ポラード・ロー素因数分解法のアルゴリズム
5. ナイーブな実装との比較

ミラー・ラビン素数判定法

ミラー・ラビン素数判定法は、与えられた自然数が素数かどうかを判定する乱択アルゴリズムです。

補題

任意の素数 $p$ と 自然数 $x$ について $x^2 \equiv_{p} 1$ と仮定すると、以下が成り立ちます。²
$$x \equiv_{p} \pm 1$$

証明
素数 $p$ と互いに素な $x$ について $x^2 \equiv_{p} 1$ と仮定。このとき以下が成り立つ。

x^2 - 1 \equiv_{p} 0\\
(x+1)(x-1) \equiv_{p} 0

$p$ は素数であるため $x+1 \equiv_{p} 0$ または $x-1 \equiv_{p} 0$ である。
よって $x \equiv_{p} \pm 1$ が成り立つ。

ミラー・ラビン素数判定法のアルゴリズム

偶数については、与えられた数が $2$ であれば素数、そうでなければ合成数であると簡単に判断できるので、以下では奇数のみが与えられるとします。

任意の奇素数 $p$ について、ある自然数 $s$ と奇数 $d$ が存在して、 $p-1 = 2^sd$ が成り立ちます。

フェルマーの小定理より $p$ と互いに素である任意の自然数 $a$ について以下が成り立ちます。
$$a^{2^sd} = a^{p-1} \equiv_{p} 1$$

補題より、以下が成り立ちます。
$$a^{2^{s-1}d} \equiv_{p} \pm 1$$

また $s>1$ であるとき $a^{2^{s-1}d} \equiv_{p} 1$ と仮定すると補題より、以下が成り立ちます。
$$a^{2^{s-2}d} \equiv_{p} \pm 1$$

このように繰り返して補題を適応していくと、任意の奇素数 $p$ と、 $p$ と互いに素である任意の自然数 $a$ について
$$a^{d} \equiv_{p} 1$$
またはある整数 $0 \le r \lt s$ が存在して
$$a^{2^rd} \equiv_{p} -1$$
が成り立ちます。

反対に自然数 $n$ と、 $n$ と互いに素なある自然数 $a$ について上記がどちらも成り立たない場合は $n$ は合成数となります。つまり、 $n$ と互いに素なある自然数 $a$ と $n-1 = 2^sd$ なる $s,d$ について
$$a^{d} \not\equiv_{n} 1$$
かつ任意の整数 $0 \le r \lt s$ について
$$a^{2^rd} \not\equiv_{n} -1$$
が成り立つ時、 $n$ は合成数となります。

ミラーラビン素数判定法では、与えられた自然数 $n$ に対して、上記が成り立つかをいくつかの $a$ について試して素数判定を行います。

与えられた数が合成数であれば、ひとつ $a$ を試すと $3/4$ 以上の確率でそれが合成数であると判断できるので、繰り返しテストを行うことで正しく判定できる確率を限りなく $1$ に近づけることができます。

具体例
$n = 4033$ とします。 まず
$$4033-1 = 4032 = 64\times63 = 2^6\times63$$
より、 $s = 6, d = 63$ となります。 $a$ として $2$ を試すと以下のようになります。

\begin{align}
2^{2^0\times63} = 2^{63} &\equiv_{4033} 3521 \\
2^{2^1\times63} = 2^{126} &\equiv_{4033} 4032\\
2^{2^2\times63} = 2^{252} &\equiv_{4033} 1 \\
2^{2^3\times63} = 2^{504} &\equiv_{4033} 1 \\
2^{2^4\times63} = 2^{1008} &\equiv_{4033} 1 \\
2^{2^5\times63} = 2^{2016} &\equiv_{4033} 1
\end{align}

$4032 \equiv_{4033} -1$ より、
$$2^{2^1\times63} \equiv_{4033} -1$$
が成り立つので $a=2$ では $4033$ が合成数かどうかは判断できません。

続いて $a=3$ を試してみると以下のようになります。

\begin{align}
3^{2^0\times63} = 3^{63} &\equiv_{4033} 3551 \\
3^{2^1\times63} = 3^{126} &\equiv_{4033} 2443\\
3^{2^2\times63} = 3^{252} &\equiv_{4033} 3442 \\
3^{2^3\times63} = 3^{504} &\equiv_{4033} 2443 \\
3^{2^4\times63} = 3^{1008} &\equiv_{4033} 3442 \\
3^{2^5\times63} = 3^{2016} &\equiv_{4033} 2443
\end{align}

このように途中から $2443$ と $3442$ で循環が発生してしまい、
$$3^{63} \not\equiv_{4033} 1$$
かつ任意の整数 $0 \le r \lt 6$ について
$$3^{2^r\times63} \not\equiv_{4033} -1$$
となってしまいます。 よって、ミラー・ラビン素数判定法では $4033$ は合成数であると判断されます。
実際に $4033 = 37 \times 109$ なので正しく判断できています。

なお、与えられる数が $2^{64}$ 未満である場合、 $a$ として $2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37$ のみを試せば十分であることが分かっています。³

実装では各 $a$ に対して、 $x \equiv_{n} a^{d}, r = 0$ で初期化し、 $r<s$ の間 $x \equiv_{n} x^2, r=r+1$ と更新を繰り返していくと常に $x \equiv_{n} a^{2^rd}$ が成り立っているので、更新しながら $x \not\equiv_{n} -1$ を検証すれば良いです。

コード

def is_prime(n):
    if n == 2:  # 2であれば素数なので終了
        return 1
    if n == 1 or n%2 == 0:  # 1もしくは2より大きい偶数であれば素数でないので終了
        return 0

    m = n - 1
    lsb = m & -m  # LSB. m-1をビット列で表した時立っているビットのうち最も小さいもの
    s = lsb.bit_length()-1  # 上述のs. LSB以上のビットの部分をdとし、2^s = LSBとすると上述のp-1 = 2^sdを満たす
    d = m // lsb

    test_numbers = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37]

    for a in test_numbers:
        if a == n:  # a = n -> 任意の自然数kについてa^k ≡ 0(mod n)なので無視
            continue
        x = pow(a,d,n)  # x ≡ a^d(mod n)で初期化
        r = 0
        if x == 1:  # a^d ≡ 1(mod n)なので無視
            continue
        while x != m:  # r = 0からsまで順にx ≡ a^(2^rd) ≡ -1(mod n)を検証
            x = pow(x,2,n)
            r += 1
            if x == 1 or r == s:  # x ≡ 1(mod n) -> x^2 ≡ 1(mod n)で-1になり得ないので合成数
                return 0
    return 1  # すべてのテストを通過したら素数であるとして終了

フロイドの循環検出法に基づく約数の探索

アルゴリズム

以下では $n$ は合成数であるとします。

定数 $c \in \mathbb{Z}/n\mathbb{Z}$ を用いて擬似乱数 $\ f: \mathbb{Z}/n\mathbb{Z}\rightarrow \mathbb{Z}/n\mathbb{Z}$ を以下で定めます。
$$\ f(a) = a^2 + c \pmod{n}$$

$n$ の $2$ 以上の約数の検出は下記の様にして行えます。

1. 適当な定数 $a$ を用いて $x = a, y = a$ で初期化
2. $x = \ f(x), y = \ f(\ f(y))$ と更新を繰り返す
3. ${\rm gcd}(|x-y|, n) \gt 1$ のとき、 ${\rm gcd}(|x-y|, n)$ は $n$ の $2$ 以上の約数であるため、これを返して終了

有限回の上記ステップの繰り返しにより、 $2$ 以上の約数が検出できる理由について簡単に述べます。

まず ${\rm gcd}(|x-y|, n)$ が $n$ の約数となるのは ${\rm gcd}$ の定義から分かるかと思います。
$2$ 以上の約数の検出、すなわち ${\rm gcd}(|x-y|, n) \gt 1$ となるには $|x-y|$ と $n$ がある共通の素因数 $p$ を持つ必要があります。すなわち
$$x \equiv_{p} y$$
となる必要があります。

ここで $p$ は $n$ の素因数であるため $\ f$ を $\mathbb{Z}/p\mathbb{Z}$ 上の関数とみなしてもよいです。 すると $\mathbb{Z}/p\mathbb{Z}$ 上で $a, \ f(a), \ f(\ f(a)), ...$ は必ずどこかで循環するはずです。
よって循環部分の長さを $\mu$、非循環部分の長さを $\lambda$ とし、 $a_{k} := \ f^k(a)$ （$\ f$ を $k$ 回 $a$ に適用）と表すと任意の $k \ge \lambda$ と整数 $d$ について、
$$a_{k} \equiv_{p} a_{k+d\mu}$$
が成り立ちます。

また上記のステップ2.を行なった回数を $i$ とすると $x=a_{i}, y=a_{2i}$ が成り立ちます。
添字の差分に着目すると、 $2i-i=i$ より、ステップ2.を繰り返すたびに $1$ ずつ添字の差分が増えていきます。よって $i \ge \lambda$ かつ $i$ が $\mu$ の倍数となったタイミングで、
$$x \equiv_{p} y$$
が成り立ちます。よって $|x-y|$ と $n$ がどちらも $p$ の倍数となり ${\rm gcd}(|x-y|, n) \gt 1$ が成り立つため、有限回の上記ステップの繰り返しにより $n$ の $2$ 以上の約数を見つけることができます。

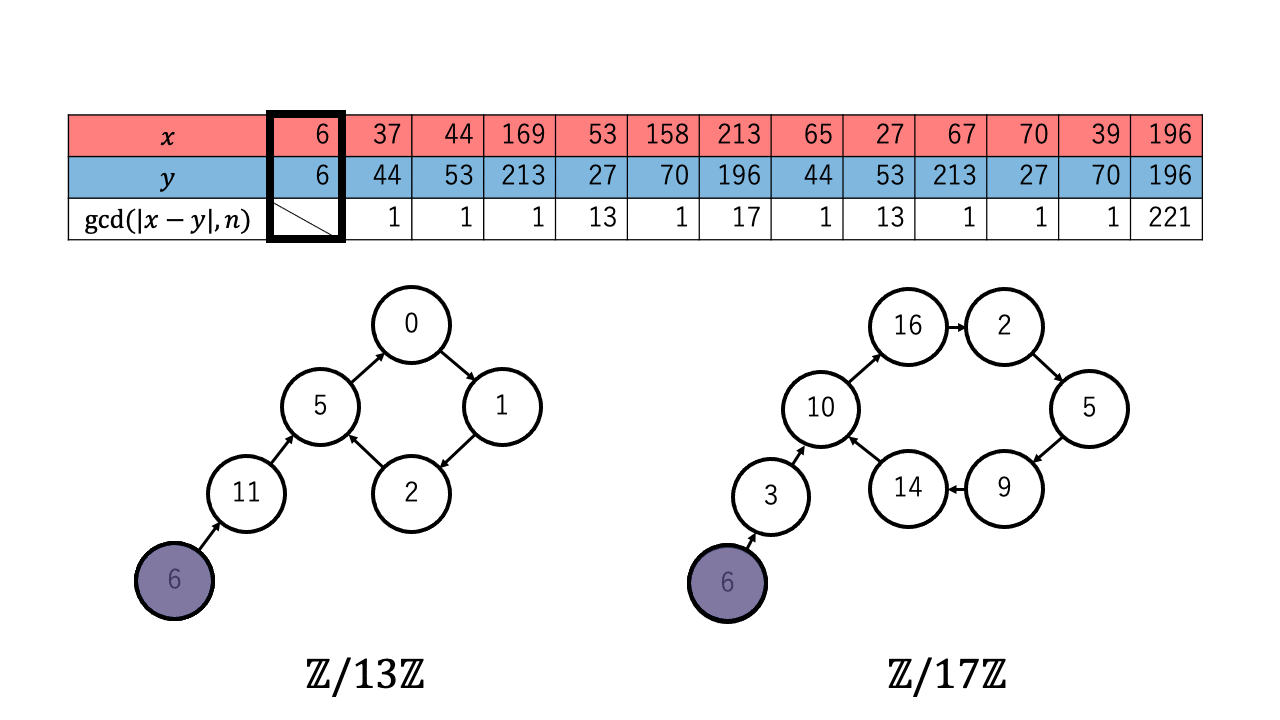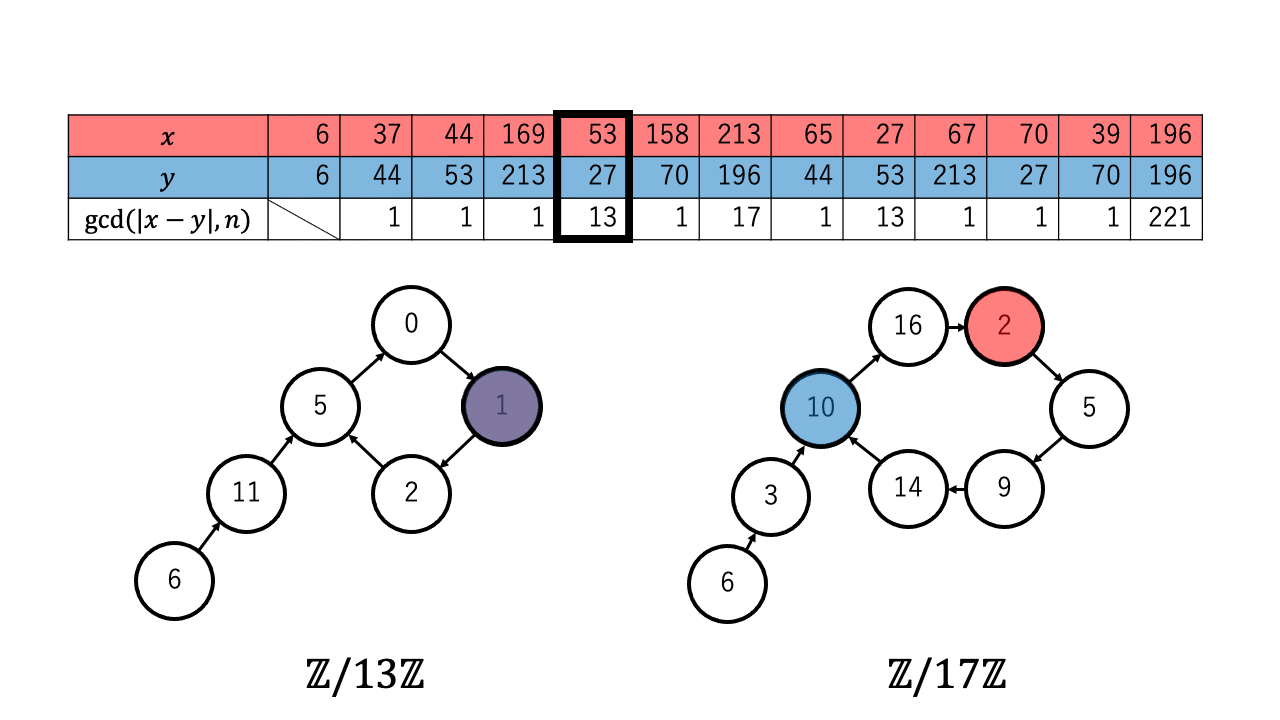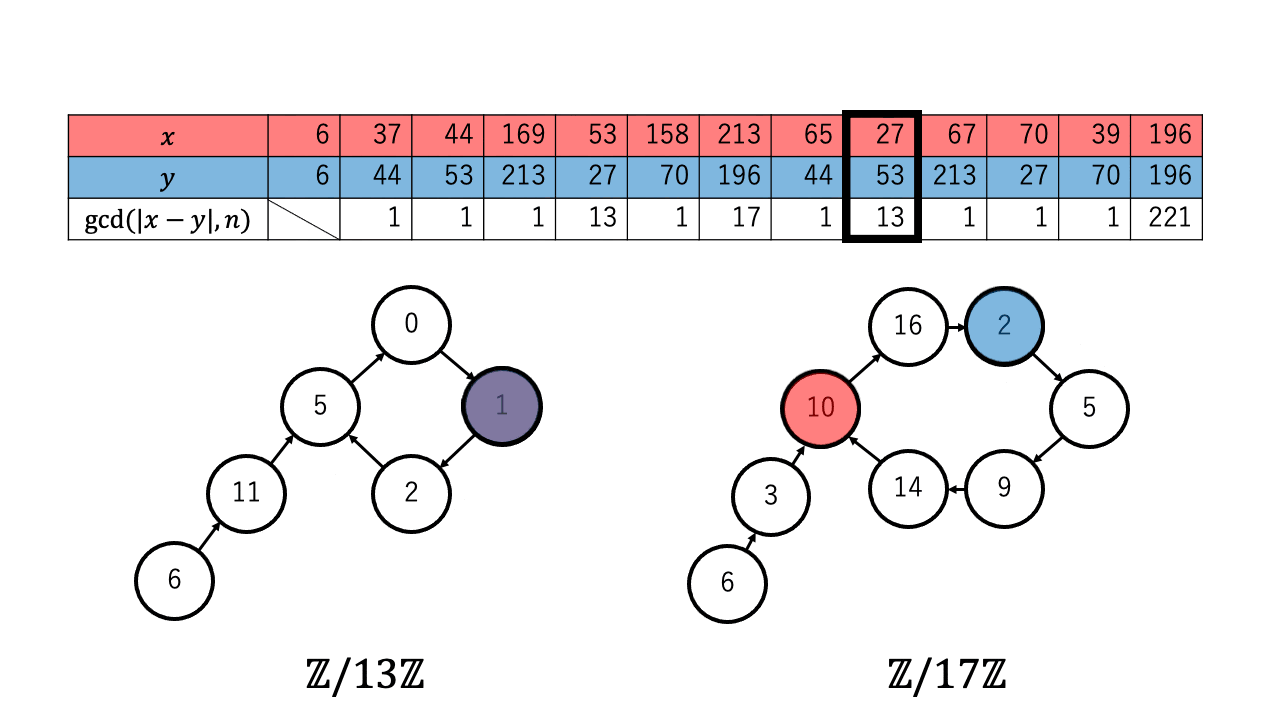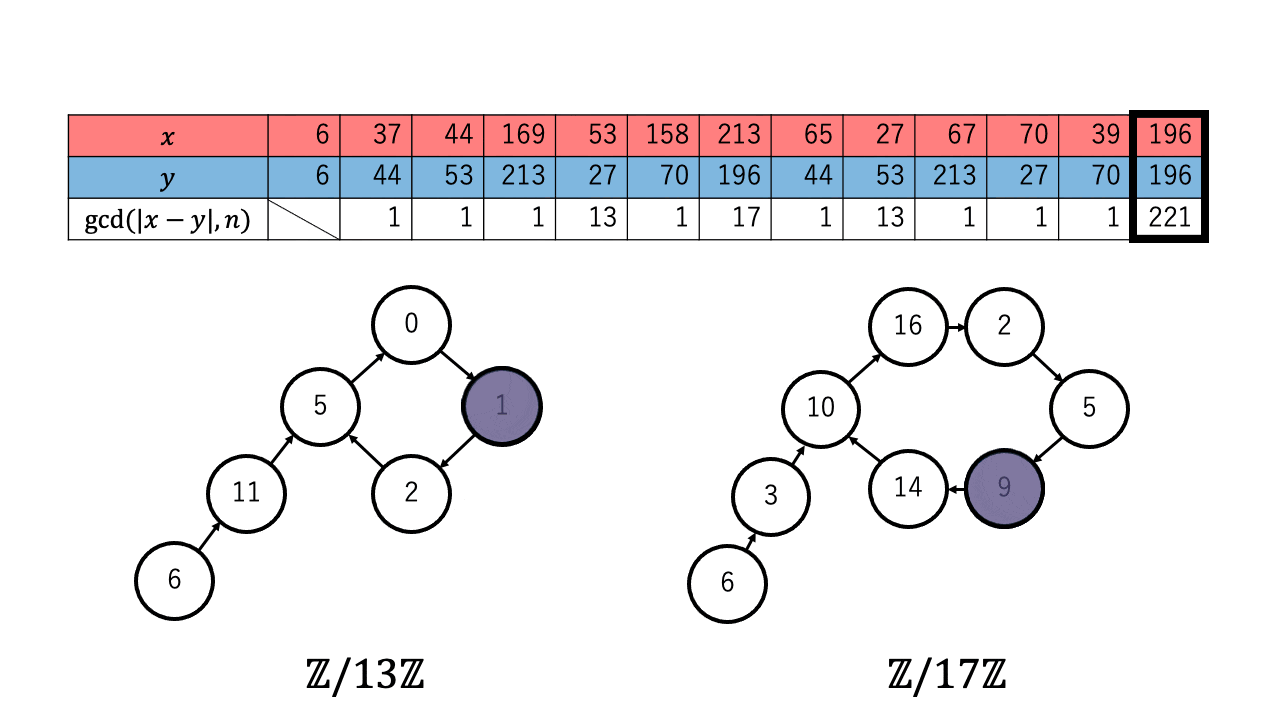
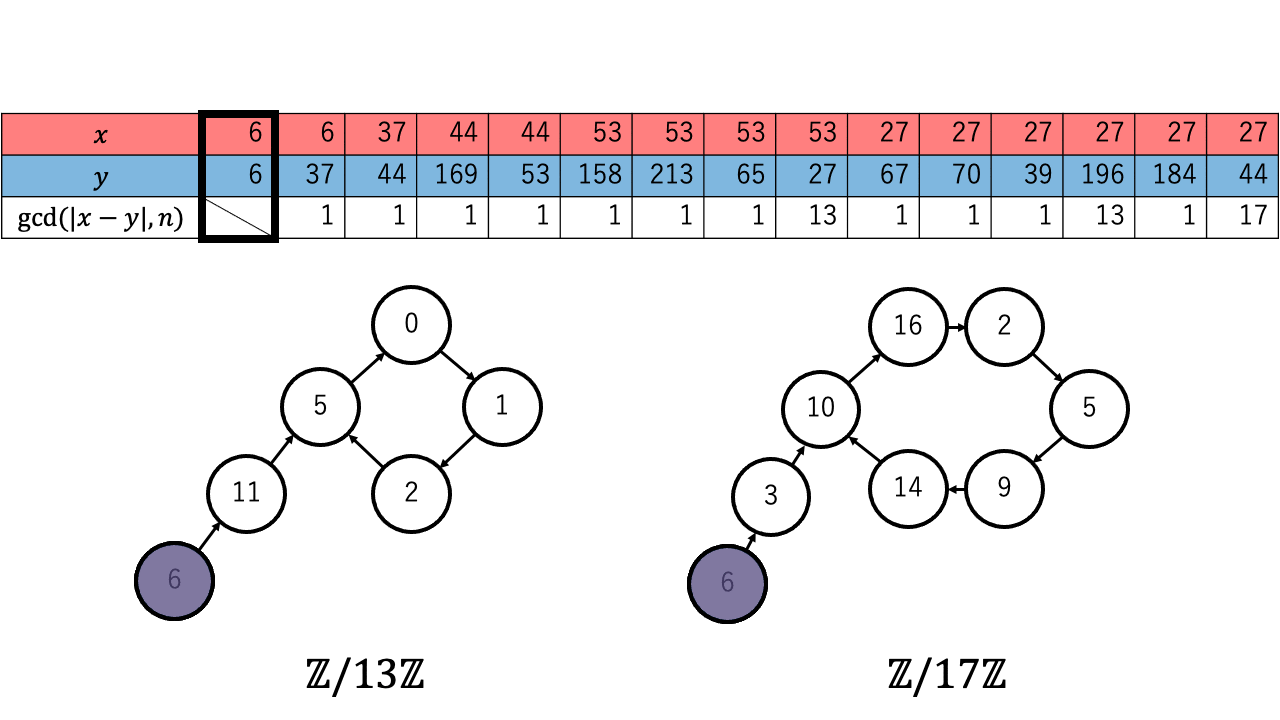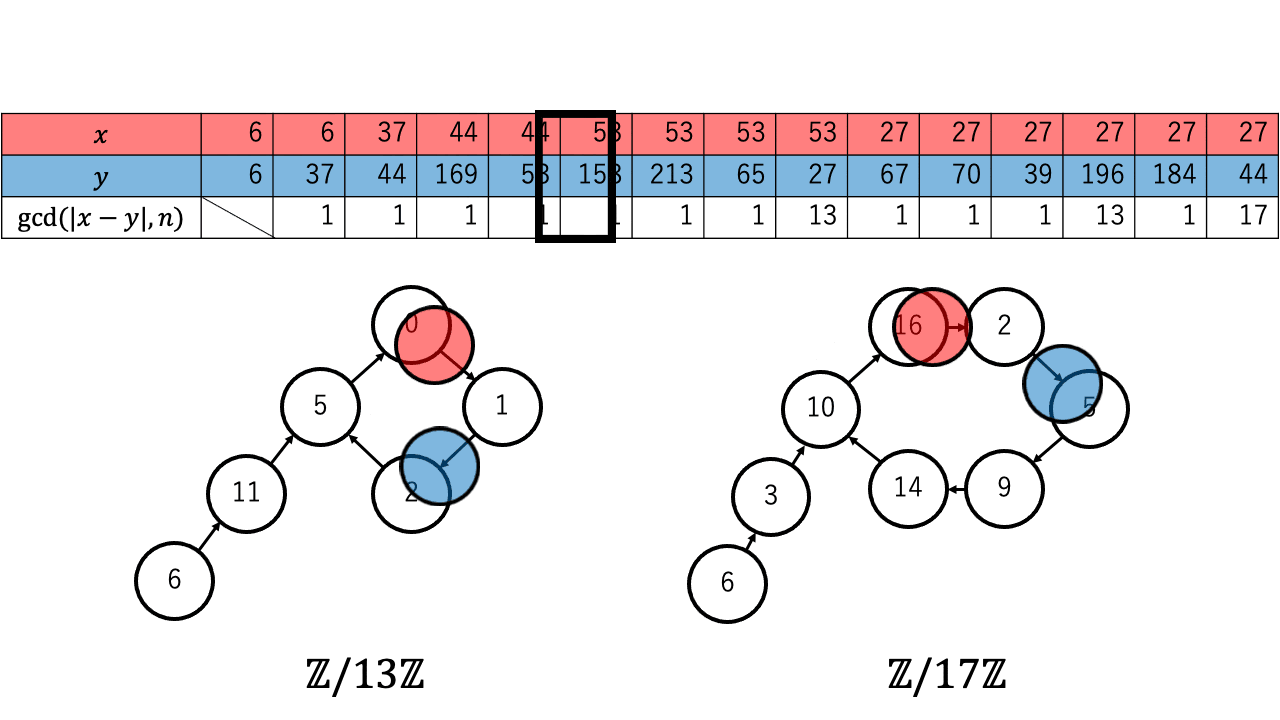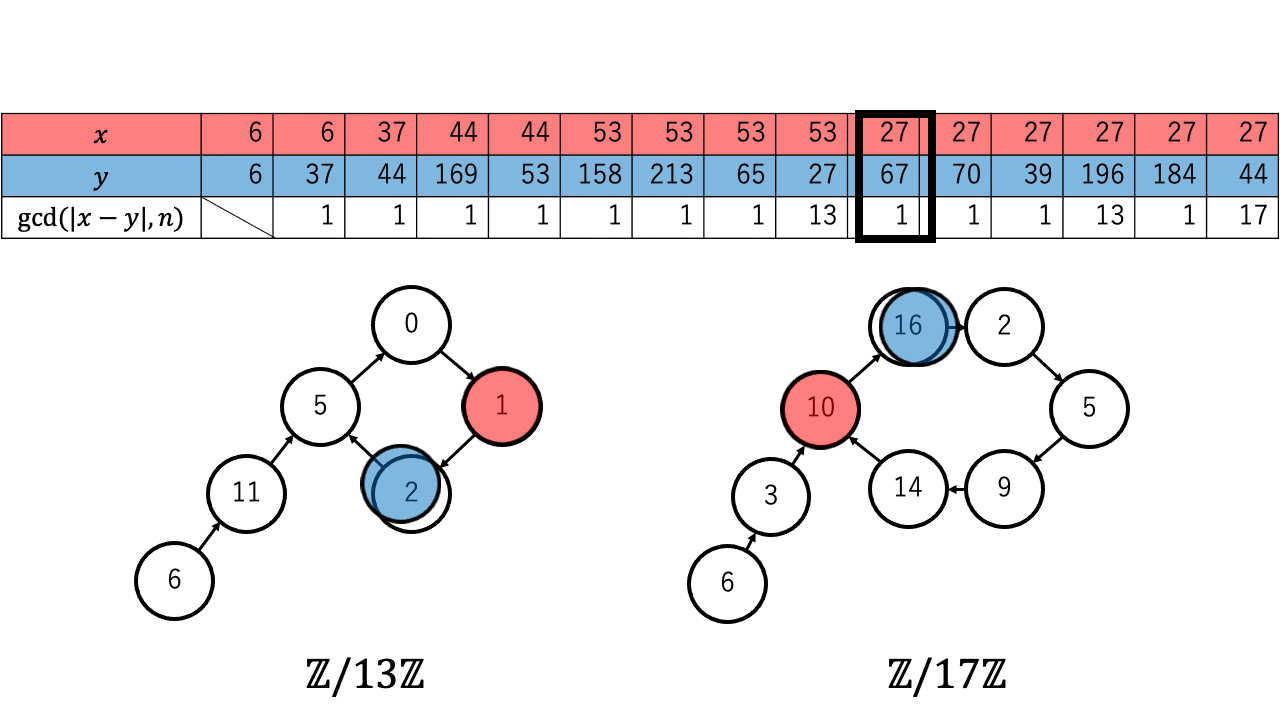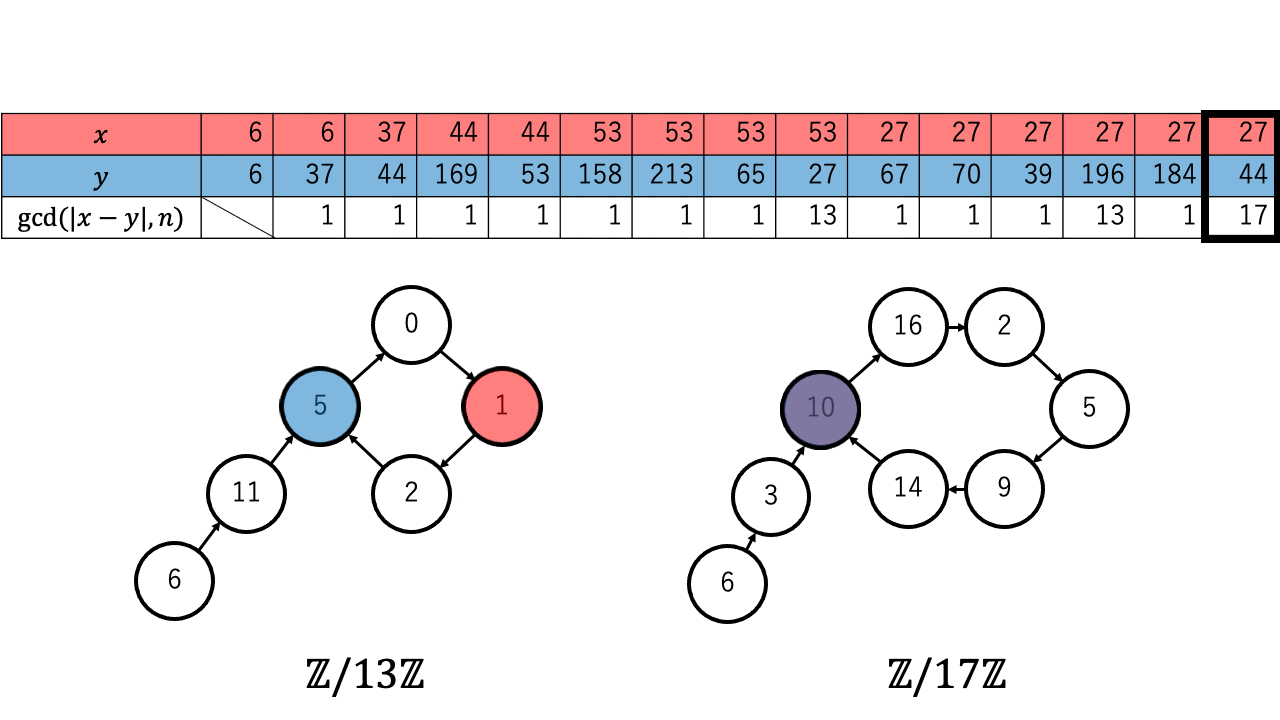
以下は $n=221=13\times17$ 、擬似乱数を $\ f(a) = a^2 + 1 \pmod{n}$、 $x,y$ の初期値を $6$ としたときの約数を検出するステップのアニメーションです。 赤色が $1$ つずつ進む $x$ で、青色が $2$ つずつ進む $y$ です。

$p \in \{13,17\}$ について $x \equiv_{p} y$ となったとき、つまり $\mathbb{Z}/p\mathbb{Z}$ 上で $x$ （赤）と $y$ （青）が重なった時、 ${\rm gcd}(|x-y|,n)$ が $n$ の $2$ 以上の約数となっているのが確認できます。⁴

なお $2$ 以上の約数が見つかるまでの計算回数についてですが、擬似乱数 $\ f$ の偏りが十分に小さく真の乱数列のように動くとみなすと、 $1.177\sqrt{p}$ 回以上 $x$ と $y$ の更新を繰り返したとき $\mathbb{Z}/p\mathbb{Z}$ 上で $x$ と $y$ が一致する（$x \equiv_{p} y$ となる）確率が $1/2$ を超えます。⁵
実際に上記のアニメーションからも $p = 13$ について、 $4 (\lt 4.244 =1.177\sqrt{13})$ 回の繰り返しで $x$ と $y$ が一致しているのが確認できます。

$n$ は合成数であれば必ず $\sqrt{n}$ 以下の素因数をもつので $O(n^{1/4})$ 回の繰り返し、 また ${\rm gcd}$ の計算で $O(\log n)$ かかるので、計算量 $O(n^{1/4}\log n)$ で半分以上の確率で約数の検出を行うことができます。

素因数の探索

$n$ の素因数を求めたいときは約数 $m$ を探したあとに、 $m$ もしくは $n/m$ のどちらかが素数であればそれを返して、 そうでなければ $n=m$ として、再び約数を探すというのを素数が見つかるまで繰り返せば良いです。

擬似乱数 $\ f(a) = a^2 + c \pmod{n}$ の定数 $c$ の取り方によっては $n$ の全ての約数について循環の検出にかかる繰り返し回数が一致してしまい、${\rm gcd}(|x-y|,n)$ が $n$ になってしまうことがあります。
この場合は約数として $m=n$ が見つかってしまうので、上記のように再帰的に約数を求めることができないのですが、定数 $c$ の値を変えて擬似乱数の動きを変え、再度 $n$ について約数の探索を行えば良いです。

コード

def gcd(a, b):
    while a:
        a, b = b%a, a
    return b


def find_prime_factor(n):
    if n%2 == 0:  # 偶数なら素因数2を返して終了
        return 2

    for c in range(1,n):
        f = lambda a: (pow(a,2,n)+c)%n  # 擬似乱数
        x = y = 0
        g = 1
        while g == 1:  # x = f(x),y = f(f(y))にそれぞれ更新しながらgcd(|x-y|,n)>1を検証
            x = f(x)
            y = f(f(y))
            g = gcd(abs(x-y),n)
        if g == n:  # gcd(|x-y|,n)=nであればcの値を変えてもう一度繰り返す
            continue
        if is_prime(g):  # gcd(|x-y|,n)が素数であればgcd(|x-y|,n)を返して終了
            return g
        elif is_prime(n//g):  # n/gcd(|x-y|,n)もまたnの約数なので同様に素数であればn/gcd(|x-y|,n)を返して終了
            return n//g
        else:  # gcd(|x-y|,n), n/gcd(|x-y|,n)が素数でなければgcd(|x-y|,n)に対して再帰的に約数を探索
            return find_prime_factor(g)

リチャード・ブレントによる変形

ブレントの循環検出法

上記のフロイドの循環検出法に基づく約数の探索方法ではステップ2.の繰り返し回数 $i$ が非循環部分の長さ $\lambda$ 以上、さらに循環部分の長さ $\mu$ の倍数である必要があったため、 少なくとも $3{\rm max}(\lambda, \mu)$ 回以上は擬似乱数 $\ f$ を計算する必要があります。（1回の繰り返しで $x$ と $y$ についてそれぞれ1回と2回ずつ $\ f$ を計算するため）

ブレントの循環検出法に基づく方法だと、擬似乱数 $\ f$ の計算回数を最大でも $2{\rm max}(\lambda, \mu)+\mu$ 程度まで減らすことができます。

ブレントの循環検出法に基づくと約数の探索は以下の様な流れになります。

1. $y=a, r=1, k=0$ で初期化
2. $x=y$ と更新
3. $k \lt r$ の間 $k=k+1, y=\ f(y)$ と更新を繰り返す。この際最初の $y$ の更新前を除いて ${\rm gcd}(|x-y|, n) \gt 1$ となるとき、 ${\rm gcd}(|x-y|, n)$ は $n$ の $2$ 以上の約数であるため、これを返して終了
4. $r=2r$ と更新してステップ2.から繰り返す

$k$ は擬似乱数 $\ f$ の計算回数に一致し、常に $y=\ f^k(a)=a_{k}$ が成り立ちます。またステップ2.により常に $x=a_{r/2}$ となります。つまりこれは、任意の2の冪 $r$ と、 $r/2 \lt k \le r$ なる $k$ について
$$x \equiv_{p} y$$
すなわち
$$a_{r/2} \equiv_{p} a_{k}$$
を検証しているということになります。

$a_{r/2} \equiv_{p} a_{k}$ が成り立つ条件はフロイドの循環検出法と同様で、それぞれの添字 $r/2, k$ が非循環部分の長さ $\lambda$ 以上かつ添字の差分 $k-r/2$ が循環部分の長さ $\mu$ と等しくなることです。⁶

ここで、$k \le r$ より $\mu = k-r/2 \le r/2$ なので、 $r/2 \ge {\rm max}(\lambda, \mu)$ のとき初めて、ある $k$ が存在して $a_{r/2} \equiv_{p} a_{k}$ が成り立ちます。
このような最小の2の冪 $r$ は ${\rm max}(\lambda, \mu) \le r/2 \lt 2{\rm max}(\lambda, \mu)$ の範囲に存在するはずなので、擬似乱数 $\ f$ の計算回数 $k$ は
$$k = r/2+\mu \lt 2{\rm max}(\lambda, \mu) + \mu$$
で上から抑えられます。

こちらも $n=221=13\times17$ 、擬似乱数を $\ f(a) = a^2 + 1 \pmod{n}$、 $x,y$ の初期値を $6$ としたときの約数を検出するステップのアニメーションを貼っておきます。 赤色が $x$ で、青色が $y$ です。

フロイドの循環検出法の方が早いステップで約数を見つけているため、フロイドの循環検出法のほうが早い様に見えますが、実際はフロイドの循環検出法では各ステップで $3$ 回ずつ擬似乱数 $\ f$ の計算を行っているため、ブレントの循環検出法のほうが早いです。
具体的には例えば約数 $13$ について、最初の検出までにフロイドの循環検出法は $3 \times 4 = 12$ 回、ブレントの循環検出法は $8$ 回、それぞれ擬似乱数 $\ f$ の計算を行っています。

なお $k \lt 3r/4$ の間は ${\rm gcd}(|x-y|, n)$ の計算を飛ばして、 残りの $3r/4 \le k \lt r$ の間だけ ${\rm gcd}(|x-y|, n)$ の計算を行うことで、さらに高速化をすることが可能です。
これは、もし $r/2 \lt k \lt 3r/4$ の間に約数が検出されるとすると、残りの $3r/4 \le k \lt r$ の間でも再度同じ約数が検出されるためです。

GCDをまとめて計算

${\rm gcd}(|x-y|, n) \gt 1$ であるとき、任意の整数 $q$ について ${\rm gcd}(q|x-y|, n) \gt 1$ もまた成り立ちます。これを用いると、
$$q=|x-y||x-f(y)||x-f(f(y))|...$$
といくつかの更新を跨いで $|x-y|$ の積を計算し、 ${\rm gcd}(q, n) \gt 1$ かどうかを見れば、 一回の計算に $O(\log n)$ かかってしまう ${\rm gcd}$ の計算回数を減らすことができます。

もし、まとめすぎて複数の約数が同時に検出され ${\rm gcd}(q, n) = n$ となってしまった場合は、ひとつ前の $q$ の状態に戻ってひとつずつ ${\rm gcd}(|x-y|, n)$ を計算すれば良いです。

ブレントの循環検出法に基づいた場合でもフロイドの循環検出法に基づいた時と同様に $O(n^{1/4})$ 回のステップの繰り返しで半分以上の確率で約数の検出を行うことができます。
したがって、まとめて計算している時の ${\rm gcd}$ の計算回数と、上記のバックトラックの際の ${\rm gcd}$ の計算回数とのバランスを考えると、まとめる数を $n^{1/8}$ 程度にしたとき、前者後者ともに ${\rm gcd}$ の計算回数が $O(n^{1/8})$ となるため、全体で $O(n^{1/4}+n^{1/8}\log n) = O(n^{1/4})$ 程度の計算量で半分以上の確率で約数の検出を行うことができます。⁷

コード

def gcd(a, b):
    while a:
        a, b = b%a, a
    return b


def find_prime_factor(n):
    if n%2 == 0:  # 偶数なら素因数2を返して終了
        return 2

    m = int(n**0.125)+1  # GCDの計算をまとめる数、O(n^(1/8))

    for c in range(1,n):
        f = lambda a: (pow(a,2,n)+c)%n  # 擬似乱数
        y = 0
        g = q = r = 1
        k = 0
        while g == 1:
            x = y
            while k < 3*r//4:  # k < 3r/4の間はGCDの計算を飛ばす
                y = f(y)
                k += 1
            while k < r and g == 1:
                ys = y  # バックトラック用の変数
                for _ in range(min(m, r-k)):  # m個まとめてGCDを計算して途中でGCD>1となったらループを抜ける
                    y = f(y)
                    q = q*abs(x-y)%n
                g = gcd(q,n)
                k += m
            k = r
            r *= 2  # GCDが1しか見つからなければr = 2rとして繰り返す
        if g == n:  # GCDがnであればバックトラックして一つずつgcd(|x-y|,n)=1を検証
            g = 1
            y = ys
            while g == 1:
                y = f(y)
                g = gcd(abs(x-y),n)
        if g == n:  # gcd(|x-y|,n)=nであればcの値を変えてもう一度繰り返す
            continue
        if is_prime(g):  # gcd(|x-y|,n)が素数であればgcd(|x-y|,n)を返して終了
            return g
        elif is_prime(n//g):  # n/gcd(|x-y|,n)もまたnの約数なので同様に素数であればn/gcd(|x-y|,n)を返して終了
            return n//g
        else:  # gcd(|x-y|,n), n/gcd(|x-y|,n)が素数でなければgcd(|x-y|,n)に対して再帰的に約数を探索
            return find_prime_factor(g)

ポラード・ロー素因数分解法のアルゴリズム

入力 $n$ に対して以下の手順により素因数分解を行います。

1. $n$ が合成数である間ステップ2.と3.を繰り返す
2. $n$ の素因数 $p$ をひとつ求める
3. $n$ を $p$ で割り切れるだけ割り続け、割った回数だけ $p$ を出力に追加する
4. $n$ が $1$ より大きければ $n$ は素数なので $n$ を出力に追加する

1.の素数判定にはミラー・ラビン素数判定法を、2.で素因数を求める際にはフロイドの循環検出法もしくはブレントの循環検出法をベースとする素因数発見手法をそれぞれ用います。

コード

def gcd(a, b):
    while a:
        a, b = b%a, a
    return b


def is_prime(n):
    if n == 2:
        return 1
    if n == 1 or n%2 == 0:
        return 0

    m = n - 1
    lsb = m & -m
    s = lsb.bit_length()-1
    d = m // lsb

    test_numbers = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37]

    for a in test_numbers:
        if a == n:
            continue
        x = pow(a,d,n)
        r = 0
        if x == 1:
            continue
        while x != m:
            x = pow(x,2,n)
            r += 1
            if x == 1 or r == s:
                return 0
    return 1


def find_prime_factor(n):
    if n%2 == 0:
        return 2

    m = int(n**0.125)+1

    for c in range(1,n):
        f = lambda a: (pow(a,2,n)+c)%n
        y = 0
        g = q = r = 1
        k = 0
        while g == 1:
            x = y
            while k < 3*r//4:
                y = f(y)
                k += 1
            while k < r and g == 1:
                ys = y
                for _ in range(min(m, r-k)):
                    y = f(y)
                    q = q*abs(x-y)%n
                g = gcd(q,n)
                k += m
            k = r
            r *= 2
        if g == n:
            g = 1
            y = ys
            while g == 1:
                y = f(y)
                g = gcd(abs(x-y),n)
        if g == n:
            continue
        if is_prime(g):
            return g
        elif is_prime(n//g):
            return n//g
        else:
            return find_prime_factor(g)


def factorize(n):
    res = {}
    while not is_prime(n) and n > 1:  # nが合成数である間nの素因数の探索を繰り返す
        p = find_prime_factor(n)
        s = 0
        while n%p == 0:  # nが素因数pで割れる間割り続け、出力に追加
            n //= p
            s += 1
        res[p] = s
    if n > 1:  # n>1であればnは素数なので出力に追加
        res[n] = 1
    return res

ナイーブな実装との比較

冒頭に述べた $2$ 以上 $\sqrt n$ 以下の整数で順番に試し割りするナイーブな実装との比較を行います。
$1$桁から$19$桁のそれぞれの桁についてランダムな$100$個の整数に対してナイーブな実装とポラード・ロー素因数分解法でそれぞれ素因数分解を行い、その平均時間を比較します。

以下がその結果で、赤色の折れ線がナイーブな実装、青色の折れ線がポラード・ロー素因数分解法です。また使用した計算機は MacBook Pro（2.0 GHz クアッドコア Intel Core i5, 16 GB RAM）です。

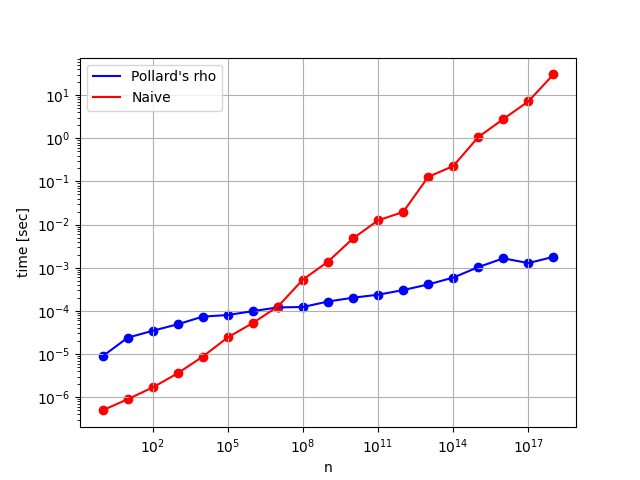
$5$桁、つまり$10^4$以下だとナイーブな実装の方が$10$倍程度早いですが、そこから数字が大きくなるにつれて徐々にポラード・ロー素因数分解法の方が早くなっていき、最終的に$19$桁、つまり$10^{18}$周辺だと$10^4$倍も高速に素因数分解が可能です。

1. ヒューリスティックによる概算であり、正確な解析はできていないそうです。 ↩

2. $a \equiv_{n} b$ という表記は $a \equiv b \pmod{n}$ と同じ意味であり、 $a$ を $n$ で割ったあまりと $b$ を $n$ で割ったあまりが等しいことを指します。 ↩

3. 詳細な条件については Wikipedia に記載があります。 ↩

4. この循環の形状がポラード・ロー（$\rho$）素因数分解法の由来だそうです。 ↩

5. これに似た話で「23人いれば、50%以上の確率で同じ誕生日の二人組が存在する」という一般的な直感と反している誕生日のパラドックスというものがあります。 ↩

6. フロイドの循環検出法では $k-r/2$ が $\mu$ の倍数であるという条件でしたが $k-r/2$ が常に $1$ から始まって $1$ ずつ増加するということを考えると、この条件は $k-r/2=\mu$ に言い換えられます。 ↩

7. ${\rm gcd}$ をまとめて計算するという手法は Pollard によって既に示されていましたが、ブレントの循環検出法と合わせることにより、フロイドの循環検出法 + ${\rm gcd}$をまとめる手法と比べて24%程度高速に動くそうです（参照）。 ↩