Go to Qiita Advent Calendar Top
LoginSignup
1
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@tRue-math

数値シミュレーションから見る『Pokémon Sleep』におけるデデンネの強さ

Last updated at Posted at 2025-12-21

この記事は、理情 Advent Calendar 2025 の 21 日目の記事です。

こんばんは、 IS25er1 の tRue です。

この前学科飲みの場で同期と少し話したネタがまあまあ面白かったので記事にしました。

本記事では、私が普段楽しくプレイしているスマホゲーム『Pokémon Sleep』に関する解析・考察をしていきます。
『Pokémon Sleep』に詳しいがコンピュータサイエンスに詳しくない、及びその逆のどちらの人にもわかりやすく書くつもりです。

§1 基礎知識 ～『Pokémon Sleep』編～

コンピュータサイエンスや数学に詳しいが『Pokémon Sleep』に詳しくない人向けの章。

『Pokémon Sleep』ってどんなゲーム？

「朝起きるのが楽しみになる睡眠ゲームアプリ」2。大きなカビゴンのいる小さな島で、「ネロリ博士」と一緒にポケモンの寝顔を研究する、と言ったストーリー。

このゲームにおける主な目標は高いスコアを取り、よりレアな寝顔を得ることです。

▼東大生が選ぶ一番かわいい寝顔(N=1)

一日の流れ

  • 昼:ポケモンたちを使役し、カビゴンを育てる
    • ポケモンたちが持ってくる「きのみ」や、 1日3回の「料理」で「カビゴンパワー」が上がる
  • 夜:なるべく長く眠る
    • 睡眠時間から「睡眠スコア」が算出される
    • だいたい8時間半眠ると100点満点が取れる
  • 朝:カビゴンのもとに集まってきたポケモンたちの寝顔を調査する
    • レアな寝顔にはより高い「ねむりパワー」が必要

「ねむりパワー」は「睡眠スコア」と「カビゴンエナジー」との積で計算されます。

つまり、このゲームで勝つ(?)には長く眠るだけではなく、カビゴンを効率的に太らせることが重要なのです。

料理について

日中、ポケモンたちは30分程度に1回ずつ「おてつだい」を行い、できのみや食材を拾ってきたり、スキルを発動したりします。この食材を使って1日3回料理をすることで、一気に大きなエナジーを稼ぐことができます。

料理を作ると稀に大成功し、得られるエナジーが大幅に増えます。
具体的には、月曜日～土曜日には10％の確率で大成功し2倍のエナジーを、日曜日には30%の確率で大成功し3倍のエナジーを得ることができます3。

▼通常時と大成功の料理エナジー

今回の記事の主題であるデデンネは、この大成功に関して特殊なバフをかけます。
これがどうやら強いことはプレイヤーの間で分かってきたのですが、果たしてどれくらい強いのかを評価する方法がなかなか難しいのです。

デデンネ(料理チャンスS)について

デデンネは2024年3月11日に『Pokémon Sleep』に実装されたポケモンで、「料理チャンスS」というスキルをもった初めてのポケモンでした。

「料理チャンスS」のスキル効果は次のように説明されています。

料理の大成功率確率が10%4上がる
効果は料理が大成功するか、フィールドを移動するまで持続する

デデンネは1日にこのスキルを2回から6回発動します(超大雑把)。単純計算で各料理の間に2回程度発動するわけですから、$10+2\times10=30$%程度で毎料理大成功するような気がするのですが…

効果は料理が大成功するか、フィールドを移動するまで持続する

ここが肝になってきます。

これは大成功するまで確率がストックされるということを意味しています。
例えば1回スキル発動して+10%の状態で料理を一度作ったとすると、20％の確率で大成功するわけですが、ここで80％を引いて大成功しなかったとき、+10%は据え置きのままです。
このまま次の料理を作れば再び20％で、さらにスキル発動すれば30％、40%の確率で大成功抽選を回すことができます。
後半のフィールド移動については、基本的には月曜の朝に行われます。なので毎週リセットされるという程度の意味だと思ってください。

簡単な考察として、例えば毎料理間に2回スキル発動するならば、大成功確率は毎回30％以上になることが保証されます。それどころか、一度大成功しなければその次は50％、さらにそれも外れれば70%という風に確率は吊り上がっていきますから、平均的な大成功確率は30％よりもかなり高くなりそうです。

▼デデンネがスキル発動する様子(かわいい)

本題について

さて、このデデンネはどれくらい強いのでしょうか？

『Pokémon Sleep』におけるポケモンの強さの比較は、主に次のような計算で行われます。

1日のおてつだい回数$\times$おてつだい1回当たりの平均エナジー貢献

ゲーム内で明記されている「おてつだい時間」から、1日にどれくらいおてつだいをするのかはすぐ計算ができます。

また、スキル発生確率(おてつだいのうちどれくらいの確率でスキルを発動するのか)もポケモンごとに固有であるので、ポケモンの強さを測るには 「スキル発動1回当たりの平均エナジー貢献」 が分かればよいわけです。

しかし、この期待値の考え方とデデンネのスキルは相性が悪いというのがわかると思います。

デデンネのスキルは直接エナジーを上げるわけではなく、「大成功確率」を上げることで間接的にエナジーに貢献します。ある種の「状態」をもったスキルと言えます。

本記事の目標は以下になります。

  • デデンネによって1週間に平均していくら大成功回数が増えるのか
    実際には日曜の大成功のみエナジーの増え幅が大きいので、料理換算で何回分増えるのかを知りたい
  • デデンネのスキル発動1回にはどれくらいのエナジー貢献度があると言えるのか

2つ目については1つ目の値を1週間のスキル発動回数で割れば直ちに求まります。
§3 では数値シミュレーションを用いてこの値を求めていきます。

§2 基礎知識 ～コンピュータサイエンス編～

あまりコンピュータサイエンスに詳しくない『Pokémon Sleep』プレイヤー向けの章です。

シミュレーションしたいこと

本記事の目標は以下を求めることです。

  • デデンネによって1週間に平均していくら大成功回数が増えるのか
    (日曜の大成功のみエナジーの増え幅が大きいので、料理換算で何回分増えるのか)

この値をデデンネの個体値、具体的には1日のスキル発動回数ごとに(10万週分くらいの)シミュレーションを用いて求めていきます。

先行研究

デデンネのスキルの強さについては様々な考察・検証が行われてきました。
例えば、実装当日のだいふく氏の動画では次のような期待値表が掲載されています。

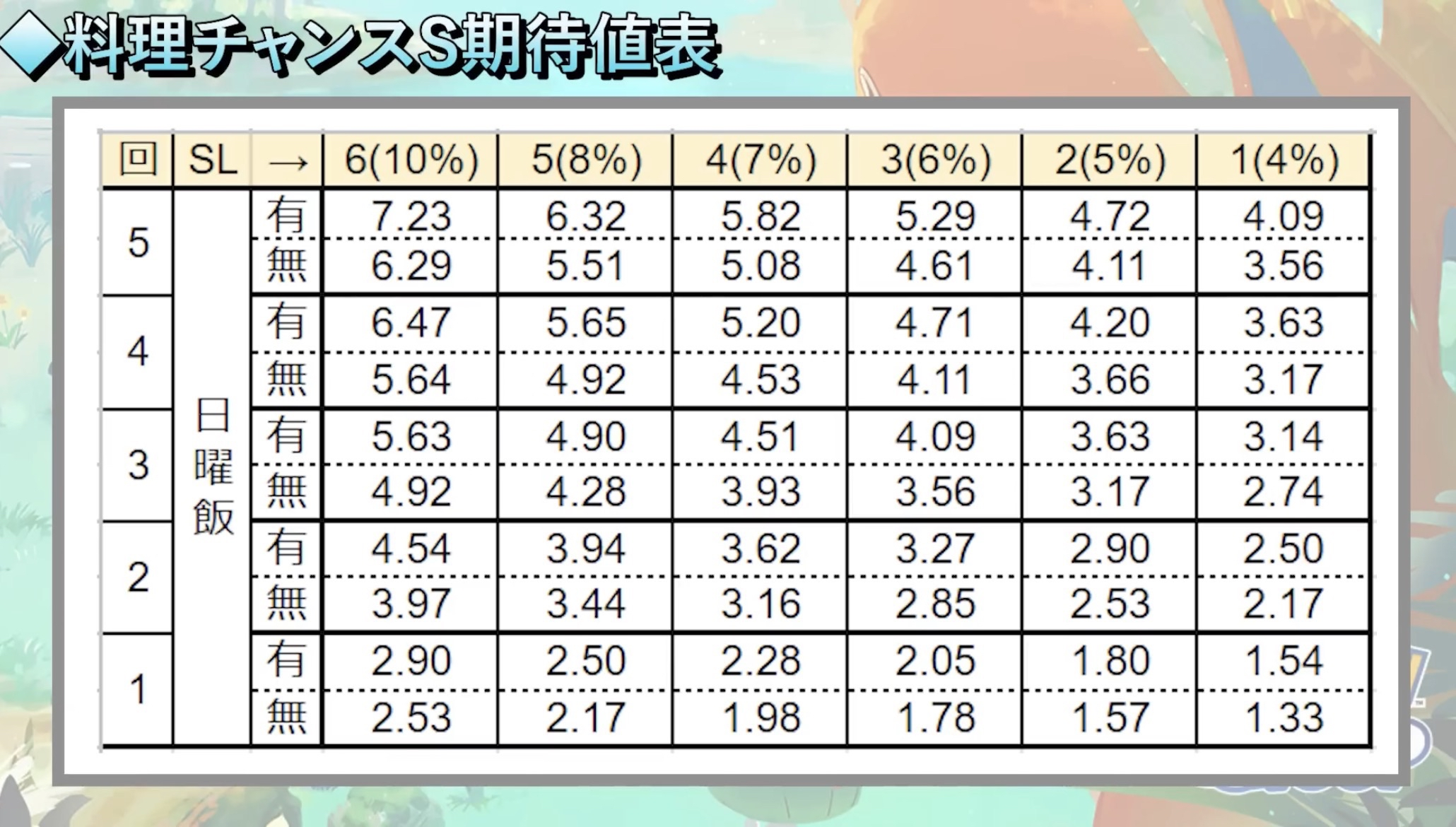
image.png
詳しくは是非本家動画の方を参照してください。
ここで求められた値は実際にデデンネを運用したプレイヤーの体感とも合致しており、本記事で求められたシミュレーション結果ともほとんど一致しています。
(実装当日にこの精度の解析が上がってるのすごすぎる)

先行研究の問題点

他にも多くの考察・検証がありますが、そのほとんどは次のような仮定を使っています。

料理間にデデンネが平均 $x$ 回スキルを発動するとき、大成功確率は $10x$ %上がる

例えば朝食から昼食の間に平均 1.5 回発動するとすれば大成功確率は 15% 上がる、というわけです。

しかし、この仮定は本当に適切でしょうか？
この部分が本記事の大きな新規性の1つでもあります。

この仮定は発動回数の散らばりを考慮できていません。

多少極端な例ですがこの仮定に従えば、毎日朝に3回、昼と夜に0回ずつ発動するような場合と朝昼夜1回ずつの場合でスキルの強さが変わらないということになります。
あまり直感的にわかるものでもない気がしますが、この結論はなんだかおかしな気がします。

実際(シミュレーションの結果)、偏って発動するよりも均等に発動した方が優位に強いため、この散らばりを考慮するようなモデルを使う必要があります。

先行研究の結果が多くのプレイヤーの体感とは大きくずれていないことからもわかる通り、この $10x$% 上がるという仮定は良い近似にはなっています。
誤った方法を取っているという指摘がしたい訳では無く、あくまでシミュレーションを回す上ではより良いモデルが存在するという指摘であることにご留意ください。

この問題を解決するコンピュータサイエンス、あるいはデータサイエンスや統計学の道具として、ポアソン分布があります。

ポアソン分布

詳しい定義や説明については他の素晴らしいブログに譲るとして、ざっくりどんなものなのか？何に使えるのか？について触れます。

上述の通り、デデンネのような状態をもつスキルのシミュレーションを行うためには実際にどの状態を取るのか、つまり各料理の瞬間に +10%, +20%, ... , +70% のいずれの状態になっているのかを具体的に持つ必要があります。

まず浮かぶシミュレーションの方法として、おてつだい1回おきにスキル確率で抽選を回すという方法があります。これは統計学的にはベルヌーイ分布を用いたシミュレーションと言うことができ、全くもって正しく適切であると言えます。

しかし我々がシミュレーションで知りたいことはデデンネのスキルによってどれくらい大成功するか、であるので、具体的にデデンネがどのタイミングでスキルを発動したか？には興味がありません。具体的には料理と料理の間で何回スキルが発動したかにのみ興味があると言えます。

このような(数学的には小さな確率のベルヌーイ分布に従う確率変数の多数の和で表せるような)値にはポアソン分布という道具が強力です。

ポアソン分布は平均 $\lambda$ 回起きるような事象が0回, 1回, ..., $n$ 回起きる確率は具体的にいくつか？を教えてくれる分布で、交通事故発生率やカフェの来客数予測などに使われるツールです。
数値シミュレーションでは(≒多くの汎用プログラミング言語では)ポアソン分布に従うような確率変数を具体的に生成することが可能で、これを用いて実際に何回事象が起きて、それによってどうなるかをシミュレーションできます。

デデンネに限らずポケスリの個体値解析では1日に平均何回スキル発動するかをスペックとして採用していますから、ポアソン分布とポケスリのシミュレーションはとても相性が良いと言えます。

例えば1日に平均3回スキル発動するデデンネがいるとして，ざっくり8時間おきに料理を作るとすれば、各料理間のスキル発動回数は $\lambda=1$ のポアソン分布に従う5と言えます。
§3 ではこのようにして用意したポアソン分布を用いて1週間に何回大成功したか？を10万週ほどシミュレーションすることで、デデンネの強さを検証しました。

§3 本題

ようやく本題です。シミュレーションを用いて求めたデデンネの強さについて解説していきます。検証に用いたコード、得られたグラフなどを挙げながら得られる結論についてまとめていきます。

また、巷で強いと評判のあの戦略についても検証しました。

シミュレーションに用いた仮定とコード

まずコードは以下です。
かなり読みやすいのでコード書いたことない人でもやりたいことはある程度分かるんじゃないかと思います。
(むしろ、コードの方が仮定などが明確に書かれているので、日本語を読むよりわかりやすいと思います。)

シミュレーションコード
dede.cpp
#include <iostream>
#include <vector>
#include <random>
#include <iomanip>
#include <cmath>
#include <string>

const int SIMULATION_WEEKS = 100000;
const double SKILL_BOOST_PERCENT = 0.10; 
const double MAX_CRIT_CHANCE = 0.70;
const int MEALS_PER_DAY = 3;

struct DayConfig {
    double base_crit_chance;
    double crit_multiplier;
};

const DayConfig WEEKDAY_CONFIG = {0.10, 2.0};
const DayConfig SUNDAY_CONFIG  = {0.30, 3.0};

std::random_device rd;
std::mt19937 gen(rd());
std::uniform_real_distribution<> dist_prob(0.0, 1.0);

double simulate_week(double triggers_per_day) {
    double total_week_multiplier = 0.0;
    double current_boost = 0.0;
    std::poisson_distribution<> dist_poisson(triggers_per_day / 3.0);

    for (int day = 0; day < 7; ++day) {
        bool is_sunday = (day == 6);
        const DayConfig& config = is_sunday ? SUNDAY_CONFIG : WEEKDAY_CONFIG;

        for (int meal = 0; meal < 3; ++meal) {
            int triggers = dist_poisson(gen);
            current_boost += triggers * SKILL_BOOST_PERCENT;

            if (current_boost > MAX_CRIT_CHANCE) current_boost = MAX_CRIT_CHANCE;
            double final_chance = config.base_crit_chance + current_boost;

            if (dist_prob(gen) < final_chance) {
                total_week_multiplier += config.crit_multiplier;
                current_boost = 0.0;
            } else {
                total_week_multiplier += 1.0;
            }
        }
    }
    return total_week_multiplier;
}

double calculate_baseline() {
    double weekday_ev = (0.10 * 2.0 + 0.90 * 1.0) * 3 * 6;
    double sunday_ev  = (0.30 * 3.0 + 0.70 * 1.0) * 3 * 1;
    return weekday_ev + sunday_ev;
}

int main() {
    double baseline = calculate_baseline();

    std::cout << "Trigger/Day, Net_Gain(Week), Value_Per_Trigger(Coeff)" << std::endl;

    for (int i = 1; i <= 100; ++i) {
        double rate = i * 0.1;
        double total_sum = 0.0;

        for (int w = 0; w < SIMULATION_WEEKS; ++w) {
            total_sum += simulate_week(rate);
        }

        double avg_total = total_sum / SIMULATION_WEEKS;
        double net_gain_week = avg_total - baseline;
        
        double total_triggers_week = rate * 7.0;
        
        double value_per_trigger = net_gain_week / total_triggers_week;

        std::cout << std::fixed << std::setprecision(1) << rate << ", "
                  << std::setprecision(4) << net_gain_week << ", "
                  << std::setprecision(5) << value_per_trigger << std::endl;
    }

    return 0;
}

さて、シミュレーションを回すにあたって用いた仮定は以下です。

  • スキル発動回数は朝昼夕食の間でちょうど3等分される
  • 各料理間のスキル発動回数は $\lambda=$1日のスキル発動回数÷3 のポアソン分布に従う
    (おてつだい時間の短さとスキル確率の小ささからポアソン分布が妥当と判断)
  • 毎食作る料理のエナジーは等しい

以上の仮定の下で10万週分のシミュレーションを回しました。

余談ですが、このコードは私 tRue ではなく、冒頭に触れた学科同期の書いたもので、「昨日話したデデンネの話だけど、シミュレーション回してみたんだよね～」みたいなノリで送られてきました。コード読みやすくてびっくりしました。

シミュレーション結果 ～デデンネの強さに対する定量的結論～

image.png

この記事の出発点とも言える画像です。10万週分のシミュレーションによってデデンネのスキル1回発動当たりの期待値を求めることに成功しています。

まずグラフの軸について説明をします。

  • 横軸(Skill Triggers per Day):
    デデンネの個体値、具体的には1日当たりの平均スキル発動回数
  • 左側の縦軸(Weekly Net Gain(x Base Meal Energy):
    1週間にわたってのデデンネによって増えたエナジー(÷料理1回のエナジー)
  • 右側の縦軸(Value per Trigger(Coefficient)):
    デデンネのスキル発動1回当たりの貢献エナジー(÷料理1回のエナジー)

デデンネによって増えたエナジーは日曜効果、つまり3倍の大成功を加味したうえでの値となっています。
また、スキル発動1回当たりの貢献エナジーは1週間で増えたエナジーを 7×(1日の平均発動回数)で割っています。

まずパッと見てわかる観察として、スキル発動1回当たりの貢献エナジーは、1日当たりの平均スキル発動回数に応じて下がるということが言えます。
言われてみれば当たり前(?6)なのかもしれませんが、エナジーチャージMなどのように直接エナジーを得るスキルと異なって、1日当たりの発動回数が2倍増えても得られるエナジーが2倍になるわけではないので、期待値はスキル発動回数が増えるほど減っていきます。

このグラフの横軸は1日に10回発動などとかなりあり得ない値まで取られていますが、それでも料理×0.15分のエナジー価値があると主張しています。
例えば食材を100個使うような大レシピなら料理1回当たり10万エナジーほど稼げますから、これを作る場合デデンネのスキル発動1回は低く見積もって15,000エナジーの価値があるということになります。
スキルレベルやフィールドボーナスを十分上げたエナチャMでも1発に得られるエナジーは11,000ほど7ですから、デデンネが最強ポケモンの一角であることは疑いようもないでしょう。

1週間における貢献度についてもいくつか重要な結果が読み取れます。
まず、先行研究で紹介しただいふく氏の期待値とは大きなズレは無く、間接的にこのシミュレーションがプレイヤーの体感ともズレていない、つまり妥当性のある結果であると言えます。例えば1日当たりスキル発動回数が4回強あれば1週間に料理7回分得する、大雑把に言えば1日1回ほど大成功すると言え、これはデデンネを使っているプレイヤーの感覚とはそれほどズレていないと思います。
また、デデンネの個体値を計算する際に非常な有用な示唆も得られます。
基本的にデデンネのスキル発動回数は2～6回程度に収まると思うのですが、1週間でのデデンネの貢献エナジーはこの範囲でおおよそ線形の振る舞いをしています。雑ではありますが、線形回帰によって次のような非常に単純な式でデデンネの貢献エナジーを計算できると言えるでしょう。

1週間に稼ぐエナジー(÷料理エナジー)$= 0.9889 \times$スキル発動回数/日$+1.843$

キャップ戦略についてのシミュレーション

シミュレーションを回すことによって、いろいろな戦略についての評価も行えるようになりました。今回は巷で話題の「キャップ戦略8」について検証しました。

キャップ戦略とは

料理チャンスSの発動について、+0%から+10%に上がるときの1回と+60%から+70%に上がる1回はどちらも同じ価値でしょうか？
直後の料理1回で得られるエナジーのみを考えるとどちらも同じ料理10%分の価値ですが、何度も述べている通り料理チャンスSの確率はストックされます。
外れた際のことを考えると、直感的には+0%からの発動の方が+60%からの発動よりも価値があるような気がします。

このような考えに基づいて、料理チャンスSによるブーストが一定の確率(例えば50%)に達したらデデンネをほかのポケモンに入れ替え、大成功したら、つまり確率がリセットされたらまたデデンネに入れ替えるという運用・戦略がプレイヤーの間で広まっています。

この運用による「デデンネを抜くことによる料理エナジーの損」と「ほかのポケモンを入れることによるエナジーの得」のどちらが大きいか、という問いもまた難しいもので、経験的に入れ替えた方がおそらく良い、とされていますがその真偽については曖昧なままでした。

シミュレーションコードと仮定

例によってコードを読むことをおすすめします。

コード
dede_cap.cpp
#include <iostream>
#include <vector>
#include <random>
#include <iomanip>
#include <cmath>
#include <string>

const int SIMULATION_WEEKS = 100000;
const double SKILL_BOOST_PERCENT = 0.10;
const double MAX_CRIT_CHANCE = 0.70;
const int MEALS_PER_DAY = 3;
const int ITER_BETWEEN_MEAL = 20;

struct DayConfig {
    double base_crit_chance;
    double crit_multiplier;
};

const DayConfig WEEKDAY_CONFIG = {0.10, 2.0};
const DayConfig SUNDAY_CONFIG  = {0.30, 3.0};

std::random_device rd;
std::mt19937 gen(rd());
std::uniform_real_distribution<> dist_prob(0.0, 1.0);

std::pair<double,double> simulate_week(double triggers_per_day, double dedenne_cap=MAX_CRIT_CHANCE) {
    double total_week_multiplier = 0.0;
    double current_boost = 0.0;
    int dedenne_rest_counts = 0;
    std::poisson_distribution<> dist_poisson(triggers_per_day / (MEALS_PER_DAY * ITER_BETWEEN_MEAL));

    for (int day = 0; day < 7; ++day) {
        bool is_sunday = (day == 6);
        const DayConfig& config = is_sunday ? SUNDAY_CONFIG : WEEKDAY_CONFIG;

        bool hungry = false;
        for (int iter = 0; iter < MEALS_PER_DAY * ITER_BETWEEN_MEAL; ++iter) {
            if (iter % ITER_BETWEEN_MEAL == 0) hungry = true;
            
            if (current_boost >= dedenne_cap) dedenne_rest_counts++;
            else {
                int triggers = dist_poisson(gen);
                current_boost += triggers * SKILL_BOOST_PERCENT;
                if (current_boost > dedenne_cap) current_boost = dedenne_cap;
            }
            
            if (hungry && iter % ITER_BETWEEN_MEAL == ITER_BETWEEN_MEAL - 1) {
                hungry = false;
                double final_chance = config.base_crit_chance + current_boost;
                if (dist_prob(gen) < final_chance) {
                    total_week_multiplier += config.crit_multiplier;
                    current_boost = 0.0;
                } else {
                    total_week_multiplier += 1.0;
                }
            }
        }
    }
    return {total_week_multiplier, dedenne_rest_counts / (double)(7 * (MEALS_PER_DAY * ITER_BETWEEN_MEAL))};
}

double calculate_baseline() {
    double weekday_ev = (WEEKDAY_CONFIG.base_crit_chance * WEEKDAY_CONFIG.crit_multiplier + (1 - WEEKDAY_CONFIG.base_crit_chance) * 1.0) * MEALS_PER_DAY * 6;
    double sunday_ev  = (SUNDAY_CONFIG.base_crit_chance * SUNDAY_CONFIG.crit_multiplier + (1 - SUNDAY_CONFIG.base_crit_chance) * 1.0) * MEALS_PER_DAY * 1;
    return weekday_ev + sunday_ev;
}

int main() {
    double baseline = calculate_baseline();

    std::cout << "Trigger/Day, " 
            << "Net_Gain_30%(Week), Rest_Rate_30%, "
            << "Net_Gain_40%(Week), Rest_Rate_40%, "
            << "Net_Gain_50%(Week), Rest_Rate_50%, "
            << "Net_Gain_60%(Week), Rest_Rate_60%, "
            << "Net_Gain_70%(Week), Rest_Rate_70%"
            << std::endl;

    for (int i = 20; i <= 60; ++i) {
        std::cout << std::fixed << std::setprecision(1) << i * 0.1 << ", ";
        for (int j = 3; j <= 7; ++j) {
            double rate = i * 0.1;
            double cap = j * 0.1;
            double total_multipler_sum = 0.0;
            double total_rest_rate_sum = 0.0;

            for (int w = 0; w < SIMULATION_WEEKS; ++w) {
                auto [multipler, rest_rate] = simulate_week(rate, cap);
                total_multipler_sum += multipler;
                total_rest_rate_sum += rest_rate;
            }

            double avg_multipler_total = total_multipler_sum / SIMULATION_WEEKS;
            double net_gain_week = avg_multipler_total - baseline;

            double avg_rest_rate = total_rest_rate_sum / SIMULATION_WEEKS;

            std::cout << std::setprecision(4) << net_gain_week << ", "
                    << std::setprecision(4) << avg_rest_rate << (j == 7 ? "" : ", ");
        }
        std::cout << std::endl;
    }

    return 0;
}

用いている仮定は以下です。

  • スキル発動回数は朝昼夕食の間でちょうど3等分される
  • 各料理間を10等分した時間でのスキル発動回数は $\lambda=$1日のスキル発動回数÷(3×10) のポアソン分布に従う
  • 毎食作る料理のエナジーは等しい

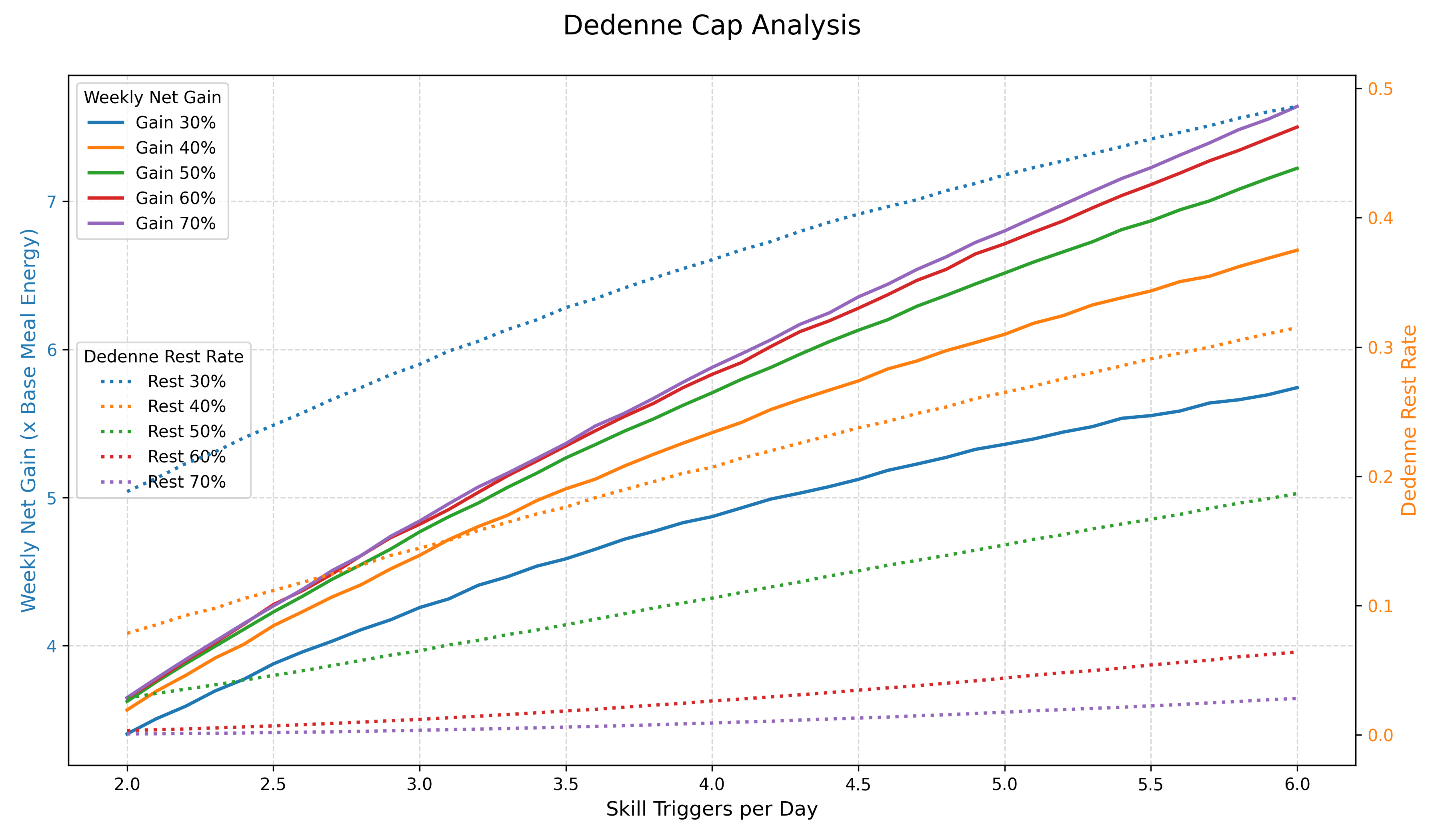
結果

image.png

グラフの軸については以下の通りです。

  • 横軸(Skill Triggers per Day):
    デデンネの個体値、具体的には1日当たりの平均スキル発動回数
  • 左側の縦軸(Weekly Net Gain(x Base Meal Energy):
    1週間にわたってのデデンネによって増えたエナジー(÷料理1回のエナジー)
  • 右側の縦軸(Dedenne Reset Rate):
    デデンネの休憩率=ほかのポケモンを入れられる割合

グラフの色が戦略、つまり+何%まで溜まったらデデンネを休憩させるかに対応しています。

グラフを見ると、巷の噂通りスキル発動1回当たりの重み、つまり10%分の価値はだんだん小さくなっていっていることが読み取れます。

特に、50%戦略と70%戦略(≒入れ替え無し)とを比較すると、1週間で高々料理 0.5 回分の差しか生まれていない一方で、休憩率は10%ほどの開きがあり、きのみタイプなどほかのポケモンに入れ替える意味が十分にあることが示されています。
より具体的に、例えば平均スキル発動回数が4.0回のデデンネの場合、一週間での損失エナジーは料理0.2回程度、対して休憩率の差は10%程度となっているため、$0.2\div( 7 \times 0.1)\simeq 0.3$ より1日当たり料理0.3回分以上のエナジーを稼げるポケモンと入れ替えれば得ということになります。
10万エナジーの料理を作るとすれば1日3万エナジーほど稼ぐポケモンなら入れ替えてOKで、きのみの数Sが付いた得意一致きのみタイプならLv30程度でも超えてくる、みたいなラインなのでプレイヤーとしての体感にも合致します。

概して、キャップ戦略は強いことが支持されたと言えるでしょう。

§4 まとめ ～Future Work～

本記事ではポアソン分布を使った数値シミュレーションを用いて、状態を持つがために解析が困難であったデデンネのスキル、料理チャンスSの強さについて定量的な評価を与えることが出来ました。また、キャップ戦略の強さについても支持できました。

今回のシミュレーションには様々な応用があり得ると考えています。

まず料理チャンスS自体の強さを評価できたことにより、ウッウやラグラージなどのスキル以外のエナジー貢献も大きい個体について、スキルの効果もきのみや食材の効果も同じエナジーという指標で測れるようになり、より汎用的で実践的な、個体の比較・検討が出来るようになったと言えます。

また、料理チャンスS以外にも状態を持つようなスキルは存在します。例えばフワライドが持つ「たくわえる(エナジーチャージS)」は何回たくわえたかによってはきだすエナジー量が変化する、状態をもつスキルです。
こちらについてもいくつかの先行研究がありますが、本記事のようなシミュレーションを回すことによってより汎用的な解析が可能になると考えています。

本記事では扱えなかった解析もいくつかあります。
まず、本記事ではポアソン分布を使って解析を行いましたが、後半のキャップ戦略の解析の時などは30分に1回程度の細かさで発動回数のチェックを行っているため、おてつだい時間が30分程度であることを考えるとシンプルにおてつだいのシミュレートを行うような、つまりベルヌーイ分布を用いたモデルでシミュレーションを行った方がより適切かもしれません。
また、実際を『Pokémon Sleep』プレイするうえでは単に期待値だけが重要なわけではなく、どれくらい上振れするのかも重要になってきます。今回はしていませんが、大成功回数などの分散を求めることでどれくらいの確率でどれくらい上振れするのか、あるいは下振れするのかなどについても、適切にシミュレーション結果を解析すれば得られると思っています。
気になった方はぜひコードを読み、書き換え、手元で実行してみてくれると嬉しいです。

今回は数値シミュレーションというアプローチでデデンネの強さを解析しましたが、もっと理論から、統計学からのアプローチで解析することも可能なのではないかと考えています。
料理チャンスSによって変動する+0,+10,...,+70%という状態を確率変数だと考えれば、これは時系列データであり、十分長い時間経った先での定常状態なら求められるのではないかと考えています。
これを使えば大成功確率はより直接的に求められそうだなと思っていますが、実際には週に高々21回の料理しか行われず、その後ストックされた確率はリセットされてしまうため、定常状態までは行かなさそうだと考え、今回の解析には不適だろうと判断しました。
数学的にはまあまあ面白い対象だと思うので、気になって解析できた人がいたら教えてください。

本記事中にも載せたコードなどは以下のレポジトリに置いておきます。
ご自由にお使いください。PR飛ばしてくれても嬉しいです。
https://github.com/tRue-math/dedenne-simulator

最後まで読んでいただきありがとうございました。
『Pokémon Sleep』神ゲーなので、やってない人は是非始めよう！

  1. 東京大学理学部情報科学科の 2025 年度入学者のこと ↩

  2. 『Pokémon Sleep』公式サイトより引用 ↩

  3. 基本値の10％についてはゲーム中で明言はされておらず、ほぼ間違いなくそうだろうと考えられている値です。 ↩

  4. 実際は10%ではなく4%や6％であることもあります。育成をすることで10％に上げることができるため、ここでは10%で紹介をしました。 ↩

  5. 正確には、デデンネのおてつだい時間が30分程度と短く、かつスキル発生率が5%程度と小さいことを持って初めてポアソン分布に従っているということが出来ます。 ↩

  6. 期待値が発動回数に応じて下がることも実はさして自明ではない気がしています、ある意味それ自体新規性のある発見だったかもしれません。 ↩

  7. 期待値チェッカーより引用。いつもお世話になっております。 ↩

  8. 私tRueが勝手にそう呼んでいる戦略です。界隈では広く知られ使われているようですが、観測した限りでは特別名付けられてはいませんでした。 ↩

1
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?