Basic Linear Algebra Subprograms (BLAS) の 行列の積 演算が、C の for 文で率直に書いたルーチンに比べ、どれ程のものか体感してみる。
背景
- 深層学習の実装を理解していくにあたり、行列の積演算を高速に行いたくなった。
- BLASは 行列の積演算が速いとの話を目にするが、実際に使ってみたことはなかった。
→ 今回 BLAS の性能を体感してみる。
BLAS について
下記Webサイトを参考にしています。
・Basic Linear Algebra Subprograms(Wikipedia)
・BLASの簡単な使い方
・CUDA Toolkit cuBLAS
・インテル(R) 数値演算ライブラリ(MKL) リファレンス・マニュアル(PDF)
openBLAS
openBLAS はマルチスレッドにて CPUの全コアを用いた並列演算を行う。
cuBLAS
cuBLAS は NVIDIA のグラフィックカードのGPU上で並列演算を行う。
測定
測定内容
-
行列の積演算 $C=αAB+βC$ $(A B C は行列、α βは スカラー値)$ を行う gemm() で測定を行う。
-
一辺 num の 正方行列(下図)で、 num を増やしていった際の 所要時間で比較する。
- 各num で5回測定し平均値をプロット。
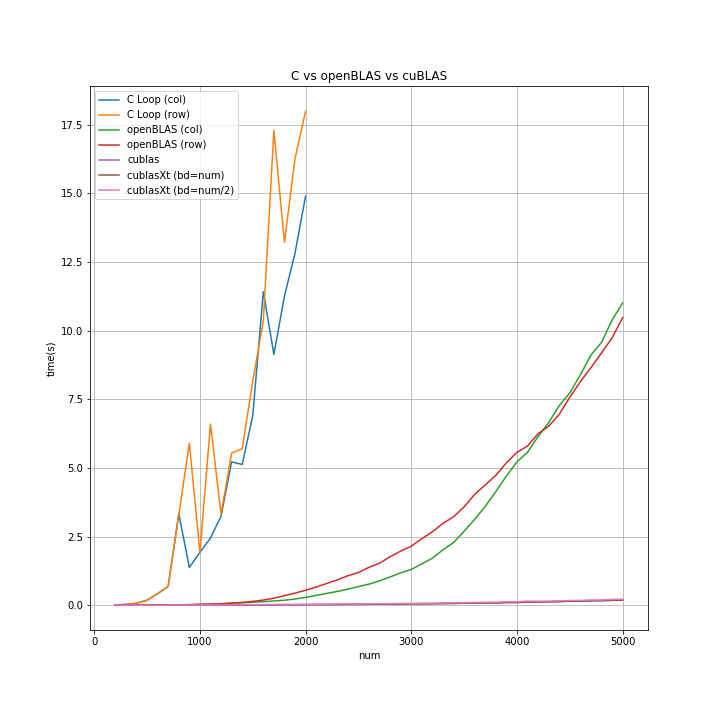
結果
グラフは下側が良く(所要時間が短い)、上側に行くほど悪い(所要時間が長い)。
(2017/5/5 追記)
グラフだけでは読み取り辛いので、num=2000の時の測定値を示します。
| 項目名 | num=2000時の所要時間(ms) | C Loop (col) を 1とした比 |
|---|---|---|
| C Loop (col) | 14902.36 | 1.00 |
| C Loop (row) | 17994.24 | 0.83 |
| openBLAS (col) | 288.02 | 51.74 |
| openBLAS (row) | 549.34 | 27.13 |
| cublas | 20.52 | 726.20 |
| cublasXt (bd=num) | 26.23 | 568.23 |
| cublasXt (bd=num/2) | 32.84 | 453.77 |
・openBLAS は C の for 文の率直版に比べ 25倍以上の差を確認しました。openBLAS すごい。予想以上でした。 C の for 文の率直版はシングルスレッドのため、openBLAS との差は 4倍~8倍(コア数~ハイパースレッド数)位かなと予想してました。25倍以上の差があるとは...。すごい。
・GPU の 並列演算 さらにすごい。gefoce1050ti な 15K円位のボードでも 率直C版に比べ 500倍以上の差を確認できました。次回 もっと詳しく見ていきます。
環境
| 項目 | 内容 |
|---|---|
| CPU | Intel(R) Core(TM) i7 CPU 920 @ 2.67GHz |
| M/B | GIGABYTE EX58-DS4 |
| メモリ | 12GB |
| グラフィックカード | 玄人志向 GF-GTX1050Ti-4GB/OC/SF |
| OS | Ubuntu 16.04 |
| グラフィックドライバ | nvidia-375 |
| CUDA | 8.0.61-1 |
| openBLAS | 0.2.18-1ubuntu1 |
| コンパイラ | gcc Ubuntu 5.4.0-6ubuntu1~16.04.4 |
ルーチン
- C loop (col) , C loop (row) のコンパイル時の最適化オプションは -O3
C の for loop での 率直な実装を示す。
C Loop (col)
# define MMCOL(X, di, i, j) ((X)[(j)*(di)+(i)])
// C Loop (Col) 部分抜粋
// hst->A , hst->B , hst->C ともに num×num×sizeof(float) の メモリ領域
gettimeofday(&st,NULL);
for(int i=0;i<num;i++)
{
for(int j=0;j<num;j++)
{
float cc = 0.0;
for(int k=0;k<num;k++)
{
cc += MMCOL(hst->A,num,i,k) + MMCOL(hst->B,num,k,j);
}
MMCOL(hst->C,num,i,j) += cc;
}
}
gettimeofday(&et,NULL);
C Loop (row)
# define MMROW(X, dj, i, j) ((X)[(i)*(dj)+(j)])
// C Loop (row) 部分抜粋
// hst->A , hst->B , hst->C ともに num×num×sizeof(float) の メモリ領域
gettimeofday(&st,NULL);
for(int i=0;i<num;i++)
{
for(int j=0;j<num;j++)
{
float cc = 0.0;
for(int k=0;k<num;k++)
{
cc += MMROW(hst->A,num,i,k) + MMROW(hst->B,num,k,j);
}
MMROW(hst->C,num,i,j) += cc;
}
}
gettimeofday(&et,NULL);
col , row 補足
- C/C++言語では行優先(row Major) だが、Fortranでは 列優先 (Column Major)。
- BLAS は 列優先 (Column Major) 。
- openBLAS は row Major も利用可能。
- cuBLAS は Column Major のみ。
BLAS の 行列の積演算の 使い方
openBLSA では cblas_sgemm 関数を、cuBLASでは cublasSgemm 関数をよぶだけ。難しいだろうと身構えていたけども、今のところ躓きはなさそう。
次回
CUDA Toolkit cuBLAS のマニュアルを読み進めると、cuBLAS に拡張を加えた cuBLAS-XT が記載されてます。
次回は cuBLAS と cuBLAS-XT の違い、どちらを使うのが良いのか的な観点で調査します。
→「cuBLAS と cuBLAS-XT の調査(その1)。行列の積演算にて」
→「cuBLAS と cuBLAS-XT の調査(その2)。行列の積演算にて。転置の影響。」