この記事は何?
機械学習の枠組みの中にランク学習(ランキング学習,Learning to Rank)というものがあります.
ランク学習のモデルの1つとして,ニューラルネットワークを用いたRankNetがあります.
この記事では,RankNetをChainerを使って実装してみましたという話をします.
予測結果を見るとなんとなく実装は正しいように思えるのですが,Chainerの使い方など間違っている点がありましたらぜひぜひご指摘を頂けると嬉しいです.
そもそもランク学習とは何だ
ランク学習では,$({\mathbf x}, y)=$(特徴量,適合度)の集合が学習されます.
適合度の大きいアイテムには大きい値を,適合度の小さいアイテムには小さい値を返すような関数$f$を学習します.
今2つのアイテム$A$と$B$が以下のように表されているとします.
A=(\mathbf{x}_A, y_A) \\
B=(\mathbf{x}_B, y_B)
また,$A$は$B$よりも適合度が大きいとします.つまり,$y_A>y_B$が成り立つとします.
このとき,関数$f$は以下の関係が成り立つように学習します.
f(\mathbf{x}_A)>f(\mathbf{x}_B)
何じゃこりゃという感じなので,ラブライブ!を使って説明します.
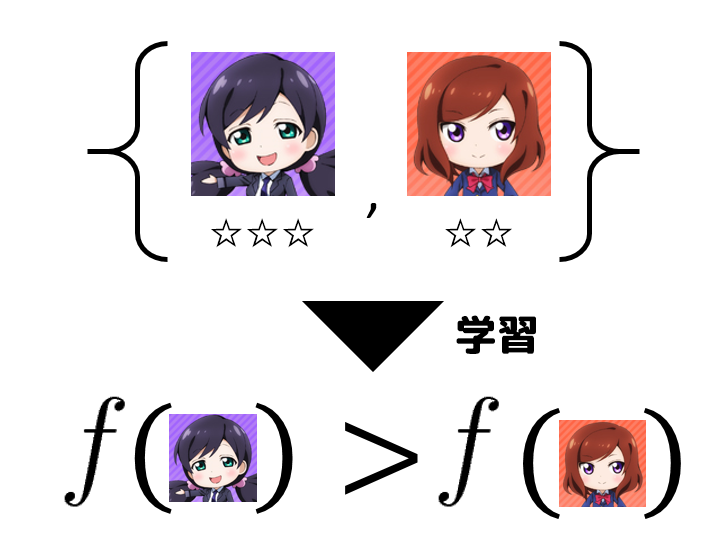
まずはラブライブ!のキャラクターに適合度(☆,☆☆,☆☆☆)を付けていきましょう.
☆の数が多いほど適合度が高い(好みである)ことを示します.
以下のペアを学習すると,こんな関数$f$が得られるはずです.
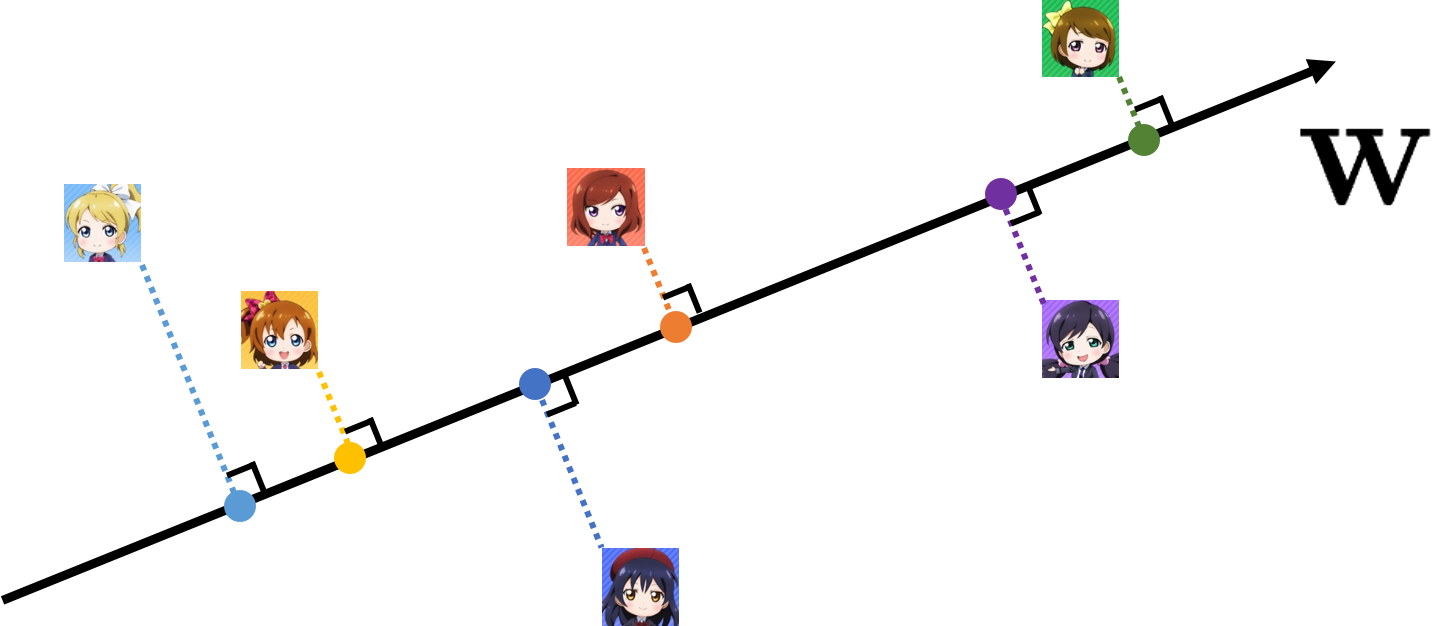
$f({\bf x})={\bf w}^T{\bf x}$のとき,重み${\bf w}$は以下の図で示されるように,特徴量が直交射影された点が適合度順に並ぶように推定されます.実際の問題では,完全に適合度順に並ぶような${\bf w}$は存在しないでしょうけど…(⇒線形分離不可能)
学習の結果得られた関数$f$を用いて,まだ適合度を付けていないキャラクターのランキングを予測することができます.
ここでは「ペアを学習する」と書きましたが,実はランク学習には大きく分けて3つの手法があり,そのうちのpairwiseという手法に当たります.他にはpointwise,listwiseといった手法がありますが,これらについては以下の資料を参考にしてください.
- DSIRNLP#1 ランキング学習ことはじめ
- [Confidence Weightedで ランク学習を実装してみた]
(http://www.slideshare.net/tkng/confidence-weighted)
RankNetについて
RankNetはニューラルネットワークに基づくランク学習のモデルであり,pairwise手法に当たります.
予測モデル自体は普通のニューラルネットワークと変わらないのですが,コスト関数の設計が異なります.といっても,コスト関数としてよく使われるクロスエントロピー関数と発想は同じです.
上と同じように,アイテム$A$と$B$がそれぞれ以下のように表されているとし,$A$は$B$よりも適合度が高いとします.
A=(\mathbf{x}_A, y_A) \\
B=(\mathbf{x}_B, y_B)
関数$f$による$A$と$B$のスコアはそれぞれ以下のように求められます.
s_A=f(\mathbf{x}_A) \\
s_B=f(\mathbf{x}_B)
RankNetが出力する,$A$が$B$よりも高くランク付けされる確率は,$s_A$と$s_B$を用いて以下のように表されます.
P_{AB}=\frac{1}{1+e^{-\sigma(s_A-s_B)}}
直感的には,$s_A$が大きくなれば$P_{AB}$は1に近づき,$s_B$が大きくなれば$P_{AB}$は0に近づくことがわかります.
$P_{AB}$を用いて,コスト関数は以下のように表されます.
C_{AB}=-\bar{P}_{AB}\log{P_{AB}}-(1-\bar{P}_{AB})\log(1-P_{AB})
ここで,$\bar{P}_{AB}$は$A$が$B$よりも高くランク付けされる既知の確率とします.
参考文献では以下のように設定されていました.
\bar{P}_{AB}=\begin{cases}
1 & (A \succ B) \\
0 & (A \prec B) \\
\frac{1}{2} & (otherwise)
\end{cases}
$C_{AB}$はまさにクロスエントロピー関数であり,$P_{AB}$が$\bar{P}_{AB}$と遠ければ遠いほど大きな値となります.RankNetではこのコスト関数を最小化するように学習します.
ChainerでのRankNetの実装
それではRankNetをChainerで実装してみようと思います.
Chainerでは損失関数softmax_cross_entropy()が実装されているのですが,softmax_cross_entropy()は目標変数としてint32型しか受け取れないため使えません.($\bar{P}_{AB}$は$\frac{1}{2}$となることがあります.)
そこで,コスト関数$C_{AB}$を自前で実装しなければならないのですが,他の損失関数では実装しているbackward()を実装しなくても学習ができてしまっていて…backward()を実装しないと自動的に数値微分するようになっているのでしょうか,お詳しい方コメントを頂けると嬉しいです.
以下RankNetの実装です,ニューラルネットワークのモデルとしては,【入力層】->【隠れ層】->【隠れ層】->【出力層】の単純な多層パーセプトロンを使っています.
from chainer import Chain
import chainer.functions as F
import chainer.links as L
class MLP(Chain):
def __init__(self, n_in, n_hidden):
super(MLP, self).__init__(
l1=L.Linear(n_in, n_hidden),
l2=L.Linear(n_hidden, n_hidden),
l3=L.Linear(n_hidden, 1)
)
def __call__(self, x):
h1 = F.relu(self.l1(x))
h2 = F.relu(self.l2(h1))
return self.l3(h2)
class RankNet(Chain):
def __init__(self, predictor):
super(RankNet, self).__init__(predictor=predictor)
def __call__(self, x_i, x_j, t_i, t_j):
s_i = self.predictor(x_i)
s_j = self.predictor(x_j)
s_diff = s_i - s_j
if t_i.data > t_j.data:
S_ij = 1
elif t_i.data < t_j.data:
S_ij = -1
else:
S_ij = 0
self.loss = (1 - S_ij) * s_diff / 2. + \
F.math.exponential.Log()(1 + F.math.exponential.Exp()(-s_diff))
return self.loss
実装したRankNetを人工データに適用してみます.
人工データは以下のように生成しました.
X=({\bf x}_1, {\bf x}_2, \dots, {\bf x}_{1000})^{\rm T} \\
{\bf y}=(y_1, y_2, \dots, y_{1000}) \\
{\bf w} = {\mathcal N}({\bf 0}, {\bf 1}) \\
y_i = uniform(1,5) \\
{\bf x}_i={\mathcal N}(0, 5) + y_i{\bf w}
50次元のデータを1000個,適合度は[1,2,3,4,5]のいずれかです.
PCA空間でプロットすると,以下の様な図となります.
なんとなく,図の左上に行くほど適合度が高く,右下に行くほど適合度が小さくなりそうです.
以下学習と評価のコードです.
学習は確率的勾配降下法を用いています,訓練データは毎回ランダムにサンプリングしています.
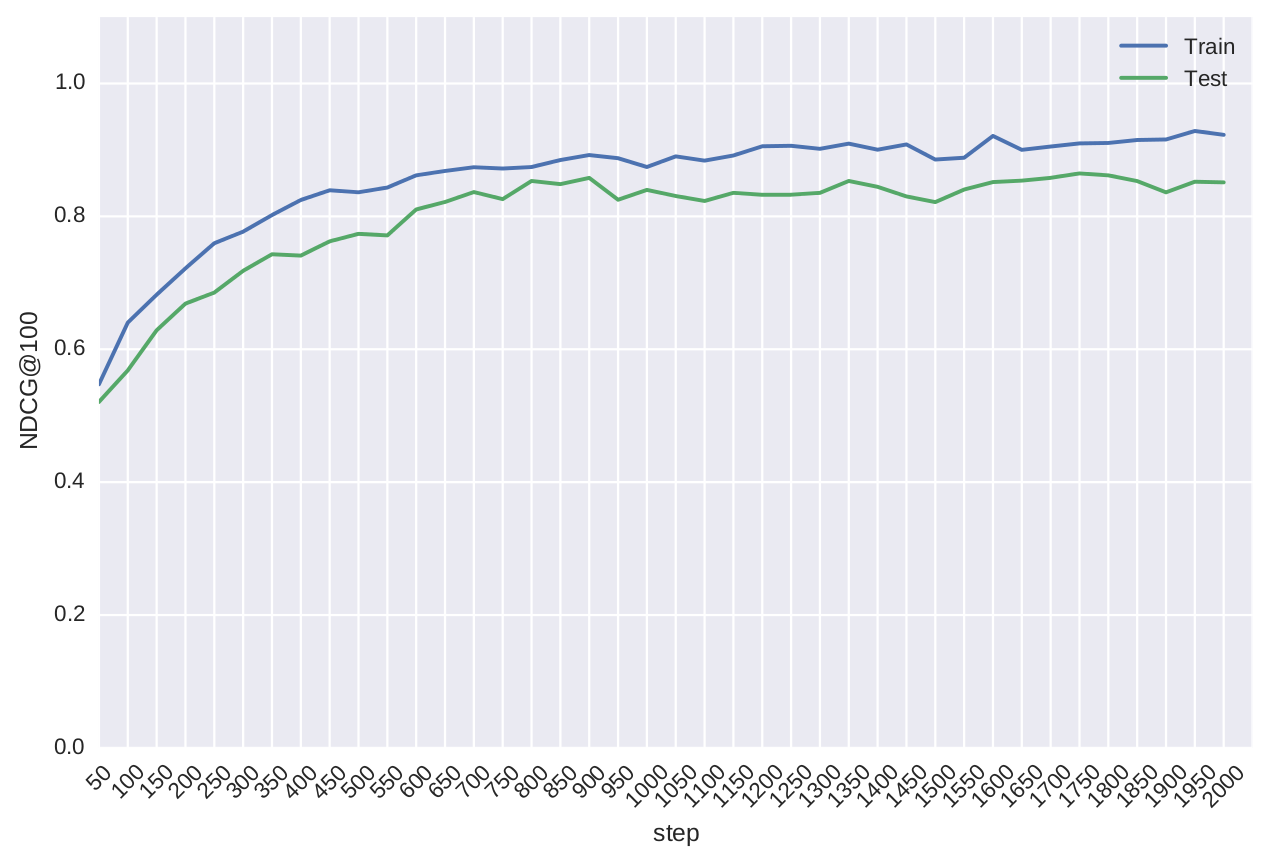
予測精度の評価はNDCG@100を用いました.
import numpy as np
from chainer import Variable, optimizers
from sklearn.cross_validation import train_test_split
import net
import matplotlib.pyplot as plt
import seaborn as sns
def make_dataset(n_dim, n_rank, n_sample, sigma):
ys = np.random.random_integers(n_rank, size=n_sample)
w = np.random.randn(n_dim)
X = [sigma * np.random.randn(n_dim) + w * y for y in ys]
X = np.array(X).astype(np.float32)
ys = np.reshape(np.array(ys), (-1, 1))
return X, ys
def ndcg(y_true, y_score, k=100):
y_true = y_true.ravel()
y_score = y_score.ravel()
y_true_sorted = sorted(y_true, reverse=True)
ideal_dcg = 0
for i in range(k):
ideal_dcg += (2 ** y_true_sorted[i] - 1.) / np.log2(i + 2)
dcg = 0
argsort_indices = np.argsort(y_score)[::-1]
for i in range(k):
dcg += (2 ** y_true[argsort_indices[i]] - 1.) / np.log2(i + 2)
ndcg = dcg / ideal_dcg
return ndcg
if __name__ == '__main__':
np.random.seed(0)
n_dim = 50
n_rank = 5
n_sample = 1000
sigma = 5.
X, ys = make_dataset(n_dim, n_rank, n_sample, sigma)
X_train, X_test, y_train, y_test = train_test_split(X, ys, test_size=0.33)
n_iter = 2000
n_hidden = 20
loss_step = 50
N_train = np.shape(X_train)[0]
model = net.RankNet(net.MLP(n_dim, n_hidden))
optimizer = optimizers.Adam()
optimizer.setup(model)
N_train = np.shape(X_train)[0]
train_ndcgs = []
test_ndcgs = []
for step in range(n_iter):
i, j = np.random.randint(N_train, size=2)
x_i = Variable(X_train[i].reshape(1, -1))
x_j = Variable(X_train[j].reshape(1, -1))
y_i = Variable(y_train[i])
y_j = Variable(y_train[j])
model.zerograds()
loss = model(x_i, x_j, y_i, y_j)
loss.backward()
optimizer.update()
if (step + 1) % loss_step == 0:
train_score = model.predictor(Variable(X_train))
test_score = model.predictor(Variable(X_test))
train_ndcg = ndcg(y_train, train_score.data)
test_ndcg = ndcg(y_test, test_score.data)
train_ndcgs.append(train_ndcg)
test_ndcgs.append(test_ndcg)
print("step: {0}".format(step + 1))
print("NDCG@100 | train: {0}, test: {1}".format(train_ndcg, test_ndcg))
plt.plot(train_ndcgs, label="Train")
plt.plot(test_ndcgs, label="Test")
xx = np.linspace(0, n_iter / loss_step, num=n_iter / loss_step + 1)
labels = np.arange(loss_step, n_iter + 1, loss_step)
plt.xticks(xx, labels, rotation=45)
plt.legend(loc="best")
plt.xlabel("step")
plt.ylabel("NDCG@10")
plt.ylim(0, 1.1)
plt.tight_layout()
plt.savefig("result.pdf")
訓練データもテストデータも同じ分布から生成してるので,当たり前と言えば当たり前なのですが,評価値が共に上がっていく様子が分かります.
その他
何か面白いもの作りたい