記事へのリンク
本記事におけるお断り
本記事は筆者が自学自習のためにデータ取得から計算までを行ったものです。特定の団体や個人から許可許諾はとっていないため、もし内容に問題があるとお考えの場合にはご連絡いただければ幸いです。
また、タイトルにもある通り、単純に強い、上手いを判断するのが困難であるポーカーにおけるスキルの『推定』がやりたかったことです。
本記事を通じて少しでもポーカーに興味を持ってアミューズメントやオンラインでポーカーを始めたいと思う人が増えれば何よりです。
実行結果
GitHubに計算した結果を格納しました。以下から参照&DL可能です。
列名等はReadMeをご覧ください。個人的な感覚では上二つがある程度良い感じの並び順だと思います
TrueSkillのエクスポース、レーティング順
TrueSkillのμ順
ELOレーティング順
仮の収支順
仮の収支順※レーキ10%
TrueSkillのσ順
出場回数順
仮の収支?
全く実力評価とは関係ないですが、全トーナメントが参加に10,000必要かつ、一般的な人数を考慮したプライズストラクチャーだった場合、
いくらの損益になっているかも計算で出しました。なお、プライズストラクチャーは以下のものを利用しました
http://sur.pokeramericas.net/help/tournaments/payout-structure.html
データの分布
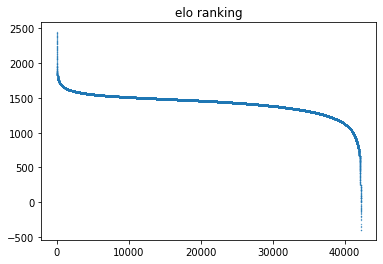
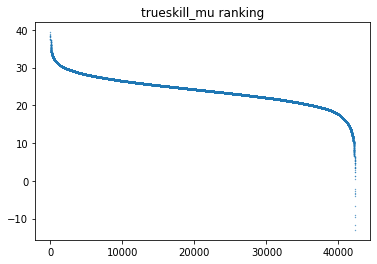
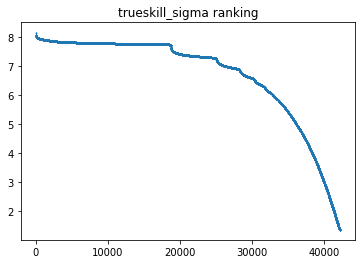
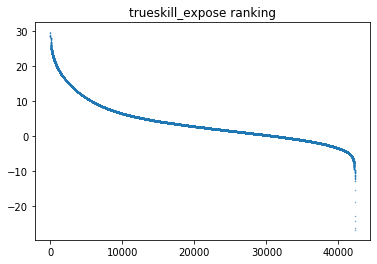
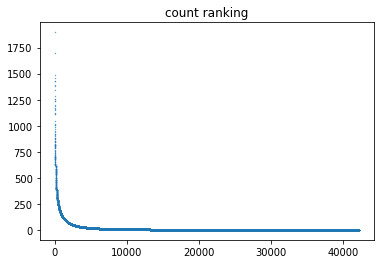
左から右へ高い順(要はランキング順)に並べたものがこちらになります。
ELOレーティング
TrueSkill
見るとわかりますが、ELOよりグラフが全体的になだらかです。
かなり運の要素が含まれ絶対的な強弱が付けづらいポーカーにおいてはこちらの方が妥当な推定ではないでしょうか。
特にExposeされたレーティングはかなりなだらかな推定が出来ています。
それ以外の指標
参加回数はこんな感じです。後で述べる通りリピーターはそこまで多くない世界なんでしょうか。
ただし、名寄せが正確に出来ていない(やっていない)ため同一人物が別人とカウントされているケースが存在しています。
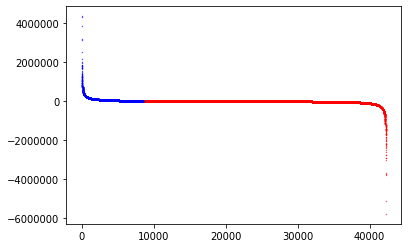
仮の収支は、収支プラスが青色、0が緑、収支マイナスを赤にしました。
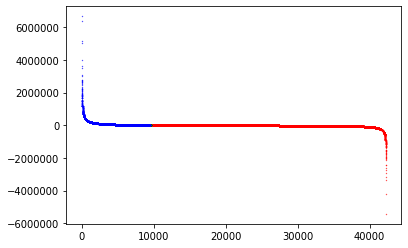
見ていて面白かったのは、10%のレーキを取っても、マイナスがプラスに変化するのはわずか2%程度だという事実です。
その割にトップの収支は2/3くらいに変化していたりと。
| 収支 | 件数(レーキ無) | 件数(レーキ有) | 比率(レーキ無) | 比率(レーキ有) |
|---|---|---|---|---|
| マイナス | 32,650 | 33,698 | 77.2% | 79.7% |
| ±0 | 185 | 5 | 0.4% | 0% |
| プラス | 9,441 | 8,573 | 22.3% | 20.3% |
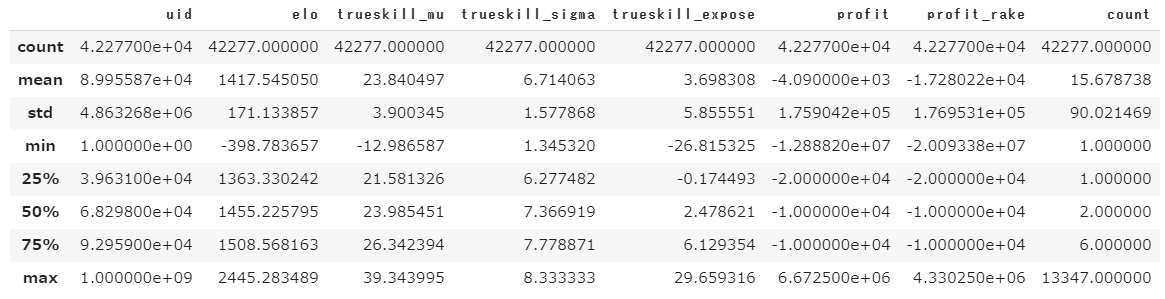
要約統計量
いくつか言える事があります
- 平均すると15.7回あたりリピートしているが、全体の半分は2回しか来ていない。
- 実際に1回10,000ポイントを賭けて戦っていたらトップは667万ポイントプラス、ビリは1,200万ポイントのマイナス
- レーキ10%による効果は、勝ち組をもっと勝たせ、負け組をもっと負けさせる効果が非常に強い。マイナスをプラスに変える力は薄い
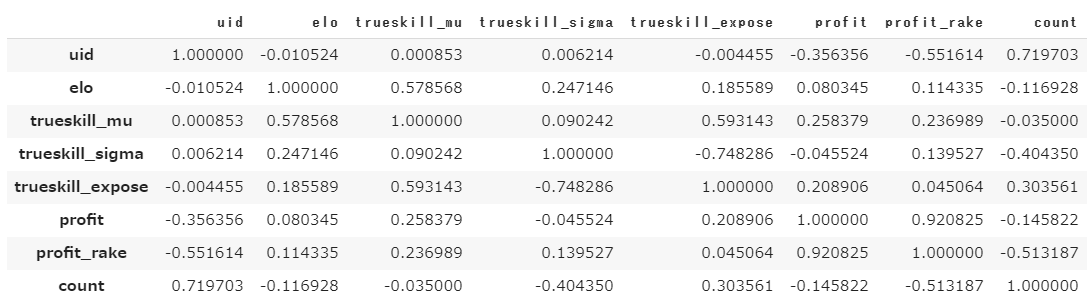
相関関係
収支がレーキの有無によって出場回数との相関係数を大きく変えています。。。
そして今回TrueSkill>ELOレーティングであることを定量的に示せる根拠がこちらかと思います。
ポーカーにおける絶対的な実力評価尺度である、収支と相関関係が強いのは、TrueSkillであることが見て取れます。
しかし、強いといってもμが0.26程度、エクスポーズは0.21程度とそこまで強くありません。
少し考えてみると、収支は出場回数に依存する数値のため、収支を出場回数で割った、1試合あたりの期待値を列で追加してみます。
すると、こちらはμで0.4の相関係数、exposeで0.33の相関係数となり、μの0.4は弱い相関~やや相関がある境目の値程度まで改善しました。
いずれにせよELOは遠く及ばない値であり、TrueSkillの優位性が改めて浮き彫りになったと思います。
最後に
アウトプットの練習も含めて、自分が興味を持てるジャンルで色々と試した結果を残してみました。
もし内容に誤りがあったり、問題がある等のご指摘あればコメントかTwitterのDMでいただければ幸いです。
ポーカーってこんな全然関係無いような事をしていても超楽しいくらい人を魅了する素晴らしいゲームです!