はじめに
この記事は古川研究室 Workout_calendar 13日目の記事です。
本記事は古川研究室の学生が学習の一環として書いたものです。内容が曖昧であったり表現が多少異なったりする場合があります。
機械学習をやりたい!というエネルギッシュな初心者(私)が必ずつまずく壁が固有値だと思うんです。
固有値は高校数学で意味わからない成りに計算させられるので、「あ、なんか行列に備わってる大事な値なんだなー」くらいの認識はあると思います。
しかし具体的にどう使うの?とか何が便利なの?とか数学で抱えがちな疑問を残したまま、記憶の彼方に置き去りにされてしまう人も多いのではないでしょうか(私)。
そして機械学習やるぞ!となったときに固有値を理解する必要に迫られ、あの時ちゃんとやってりゃ良かった...と後悔するのです(私)。
本記事の目的は、固有値がどういうものかを理解しつつ、二次形式と主成分分析という比較的簡単な応用例を実装することで、固有値がどう便利なのか、固有値は機械学習でどう使われているのかを知ろうというものです。
また、この記事は全3部作となっており、この記事はいわば前編となっています。
前編:固有値と固有ベクトルの性質←今ここ
中編:固有値と固有ベクトルの応用例(二次形式)
後編:固有値と固有ベクトルの応用例(主成分分析)
固有値ってなんだ!?!?!?!?
まず初めに固有値についてなのですが、イメージをつかむならこの記事が素晴らしくピッタリだと思います。
記事を貼り付けるだけなのも情けないのでこちらでも概要だけ説明すると
- 固有値は線形変換後の各座標の倍率
- 固有ベクトルは線形変換後も向きが変わらないベクトル
です。どういうことか直感的に理解するために次の線形変換を行ってみましょう。
\begin{equation}
\begin{pmatrix}
x^{t=2} \\
y^{t=2}
\end{pmatrix}=
\begin{pmatrix}
4 & -2 \\
1 & 1
\end{pmatrix}
\begin{pmatrix}
x^{t=1} \\
y^{t=1}
\end{pmatrix}
\end{equation}
今回は初期値($x^{t=1}$,$y^{t=1}$)=(2,3)とします。また、今後の文章の簡単化のため、右辺の2行2列の正方行列を行列$A$とします。
import numpy as np
import matplotlib.pyplot as plt
plt.figure()
A =np.array([[4,-2],[1,1]])
x=np.array([2,3])
x=np.reshape(x,(2,1))
y = np.dot(A,x)
X = 0,0
Y = 0,0
U=[y[0],x[0]]
V=[y[1],x[1]]
colors = [2,1]
plt.quiver(X,Y,U,V,colors,angles='xy',scale_units='xy',scale=1)
plt.xlim([0,5])
plt.ylim([0,5])
plt.grid()
plt.draw()
plt.show()
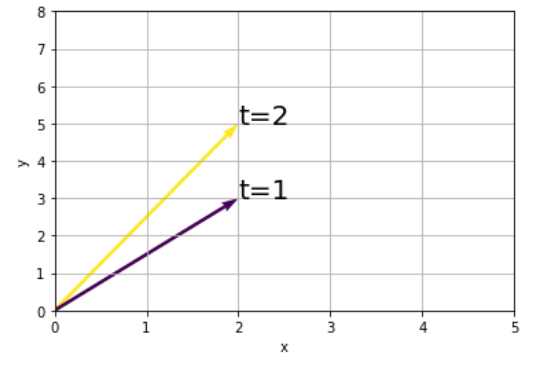
実行結果を見ると、ベクトル(2,3)が、行列$A$によって変形され、ベクトル(2,5)となっていることがわかりますね。
このような「ベクトルを行列によって変換する作業」を線形変換といいます。では同じ行列$A$を用いて別のベクトルを線形変換してみます。
\begin{equation}
\begin{pmatrix}
x^{t=2} \\
y^{t=2}
\end{pmatrix}=
\begin{pmatrix}
4 & -2 \\
1 & 1
\end{pmatrix}
\begin{pmatrix}
1 \\
1
\end{pmatrix}
\end{equation}
import numpy as np
import matplotlib.pyplot as plt
plt.figure()
A =np.array([[4,-2],[1,1]])
x=np.array([1,1])
x=np.reshape(x,(2,1))
y = np.dot(A,x)
X = 0,0
Y = 0,0
colors = [2,1]
plt.quiver(X,Y,x[0],x[1],colors[0],angles='xy',scale_units='xy',scale=1)
plt.quiver(X,Y,y[0],y[1],colors[1],angles='xy',scale_units='xy',scale=1)
plt.xlim([0,5])
plt.ylim([0,5])
plt.grid()
plt.draw()
plt.show()
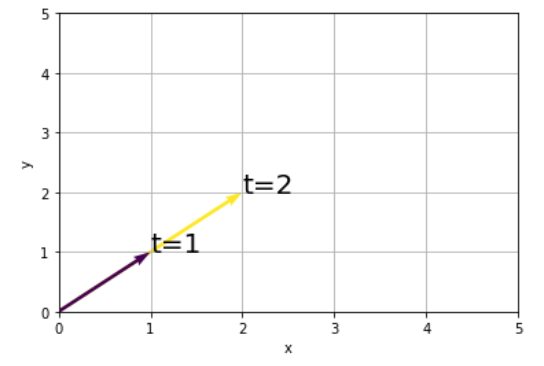
実行結果がこちらです。先ほどとは違って線形変換後もベクトルは同じ方向を向いていますね。
このような、「線形変換後も向きが変わらずに、スカラー倍されるだけのベクトル」を固有ベクトルと呼びます。固有ベクトル以外のベクトルを線形変換すると向きも大きさも変わってしまいますが、固有ベクトルだけは大きさが変化するのみなんですね。
順序が入れ替わっている気がしなくもなくもないですが、今回用いた行列$A$について固有値、固有ベクトルを導出してみます。
まずは固有値を固有方程式から算出します。
\begin{equation}
|A-\lambda I| =
\begin{vmatrix}
4-\lambda & -2 \\
1 & 1-\lambda
\end{vmatrix}
=(4-\lambda)(1-\lambda)+2
=\lambda ^2-5\lambda+6
=(\lambda-3)(\lambda-2)
\end{equation}
\begin{equation}
\lambda _1=3,\lambda _2=2
\end{equation}
続いて各固有値に対応した固有ベクトル$\mathbf{p}_1$ , $\mathbf{p}_2$を求めます。
まずは$\lambda_1=3$に対応した固有ベクトル$ \mathbf{p}_1$を求めます。
\begin{equation}
\begin{pmatrix}
4 & -2 \\
1 & 1
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}
=3
\begin{pmatrix}
x \\
y
\end{pmatrix}
\end{equation}
\begin{equation}
4x-2y=3x\\
x=2y\\
\mathbf{p}_1=
\begin{pmatrix}
2 \\
1
\end{pmatrix}
\end{equation}
同様に$\lambda_2=2$に対応した固有ベクトル$\mathbf{p}_2$を求めます。
\begin{equation}
\begin{pmatrix}
4 & -2 \\
1 & 1
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}
=2
\begin{pmatrix}
x \\
y
\end{pmatrix}
\end{equation}
\begin{equation}
4x-2y=2x\\
2x=2y\\
\mathbf{p}_2=
\begin{pmatrix}
1 \\
1
\end{pmatrix}
\end{equation}
この計算から、固有値が2,3であること、固有値2に対応する固有ベクトルは(1,1),固有値3に対応する固有ベクトルは(2,1)であることがわかりました。
先ほど線形変換したベクトルは(1,1)で返還後は(2,2)でした。つまり、固有ベクトルを線形変換すると固有値倍されるのです。
それを改めて確かめるために今度は初期値を(2,1)として試してみましょう。
import numpy as np
import matplotlib.pyplot as plt
plt.figure()
A =np.array([[4,-2],[1,1]])
x=np.array([2,1])
x=np.reshape(x,(2,1))
y = np.dot(A,x)
X = 0,0
Y = 0,0
colors = [2,1]
plt.quiver(X,Y,x[0],x[1],colors[0],angles='xy',scale_units='xy',scale=1)
plt.quiver(X,Y,y[0],y[1],colors[1],angles='xy',scale_units='xy',scale=1)
plt.xlim([0,8])
plt.ylim([0,8])
plt.grid()
plt.draw()
plt.show()
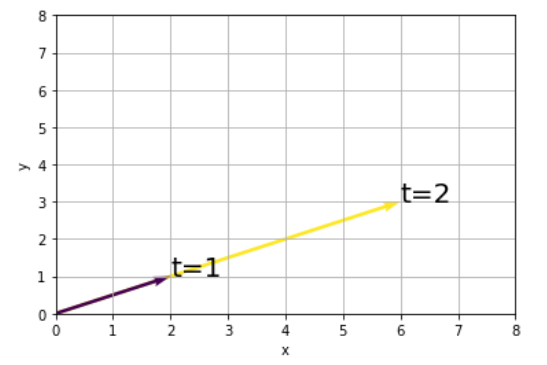
実行結果から、固有ベクトル(2,1)が固有値倍(3倍)されて現れていることがわかりました。
この結果を式で表現すると以下のようになります。
\begin{equation}
\begin{pmatrix}
4 & -2 \\
1 & 1
\end{pmatrix}
\begin{pmatrix}
2 \\
1
\end{pmatrix}
=\begin{pmatrix}
6 \\
3
\end{pmatrix}
\end{equation}
\begin{equation}
A\mathbf{p}_2=\lambda \mathbf{p}_2
\end{equation}
このような$A\mathbf{x}=\lambda \mathbf{x}$となるような固有値$\lambda$,固有ベクトル$\mathbf{x}$を求める問題を固有値問題と呼びます。
固有値問題という単語は機械学習でもしばしば用いられるので覚えておいて損はありません。
また、固有値に対する固有ベクトルは1つではありません。先ほどの例で示すとベクトル$(2,1)$をスカラー倍して得られるベクトル全てが固有ベクトルとなります。例えば$-1$倍した$(-2,-1)$とか、$2.5$倍した$(5,2.5)$とかも固有ベクトルとなります。
まとめ
本記事では固有値、固有ベクトルの性質について記述しました。
しかしこの記事を読んだ皆さんの中に
「んなるほど、確かに固有ベクトルは線形変換しても変わらない向きを表していて、固有値はその倍率だね。でも具体的にどこで使うんだいマイケル」
とお考えの方もいらっしゃると思います。
そんなあなたと私のために2本目,3本目の記事では固有値の応用例を示していきたいと思います。
前編:固有値と固有ベクトルの性質←今ここ
中編:固有値と固有ベクトルの応用例(二次形式)
後編:固有値と固有ベクトルの応用例(主成分分析)