固有値、固有ベクトルの応用例(主成分分析)

はじめに

この記事は古川研究室 Workout_calendar 13日目の記事です。
本記事は古川研究室の学生が学習の一環として書いたものです。内容が曖昧であったり表現が多少異なったりする場合があります。

また、この記事は全3部作となっており、この記事はいわば後編となっています。
前編:固有値と固有ベクトルの性質
中編:固有値と固有ベクトルの応用例(二次形式)
後編:固有値と固有ベクトルの応用例(主成分分析)←今ここ

この記事では前編の記事で軽く触れた固有値問題の例として、機械学習で用いられる次元削減法の1つである主成分分析について記していこうと思います。

主成分分析

主成分分析は、次元削減の手法の一つで多次元データを可視化する際などに使われます。
主成分分析で鍵となるのは以下に示す共分散行列です。

S = \frac{1}{N}\sum_{n=1}^N(\mathbf{x}_n-\mathbf{\bar x})(\mathbf{x}_n-\mathbf{\bar x})^T

式中の$\mathbf x_n$はD次元の各データ,$\mathbf{\bar x}$は全データの平均を示しています。
D次元データ$\mathbf x_n$を1次元空間に射影することを考えます。
また、主成分分析では、射影後のデータの分散がなるべく大きくなるように次元を削減します。
その方がデータの情報が多く残っていると判断しているわけですね。
データを射影するためにD次元のベクトルである$\mathbf{u}$を導入し、$\mathbf{u}$と$\mathbf{x}_n$の行列積を取ります。
また、$\mathbf{u}$を単位ベクトルと仮定します。つまり$\mathbf{u}^T\mathbf{u}=1$です。
射影後のデータの分散は

$$
\frac{1}{N}\sum_{n=1}^N{\mathbf{u}^T\mathbf{x}_n-\mathbf{u}\mathbf{\bar x}}^2
$$

となります。さらに式を展開していくと

\frac{1}{N}\sum_{n=1}^N(\mathbf{\mathbf{u}^T\mathbf{x}_n-u\mathbf{\bar x})(\mathbf{u}^T\mathbf{x}_n-\mathbf{u}\mathbf{\bar x})}^T

\frac{1}{N}\sum_{n=1}^N\{(\mathbf{u}^T\mathbf{x}_n)(\mathbf{u}^T\mathbf{x}_n)^T-(\mathbf{u}^T\mathbf{x}_n)(\mathbf{u}^T\mathbf{\bar x})^T-(\mathbf{u}^T\mathbf{\bar x})(\mathbf{u}^T\mathbf{x}_n)^T+(\mathbf{u}^T\mathbf{\bar x})(\mathbf{u}^T\mathbf{\bar x})^T\}

$\mathbf{(A^TB)^T=B^TA}$を各項に当てはめて整理すると

\frac{1}{N}\sum_{n=1}^N(\mathbf{u}^T\mathbf{x}_n^2\mathbf{u}-2\mathbf{u}^T\mathbf{\bar x} \mathbf{x}_n\mathbf{u}+\mathbf{u}^T\mathbf{\bar x}^2\mathbf{u})

$\mathbf{u^T,u}$を括りだして

\frac{1}{N}\sum_{n=1}^N\mathbf{u}^T(\mathbf{x}_n^2-2\mathbf{\bar x}_n \mathbf{x}_n+ \mathbf{\bar x}_n^2)\mathbf{u}\\
=\mathbf{u^T}\left \{\frac{1}{N}\sum_{n=1}^N{(\mathbf{x}_n-\mathbf{\bar x})(\mathbf{x}_n-\mathbf{\bar x})}^T\right \}\mathbf{u}
=\mathbf{u}^T\mathbf{Su}

となります。こうして得られた分散$\mathbf{u}^T\mathbf{Su}$を最大化します。$\mathbf{S}$はデータによって定まる共分散行列なので$\mathbf{u}$に対して最大化します。

$\mathbf{u}$を最大化しようとすると「$\mathbf{u}$=∞にすれば最大じゃんアハハ」と抜かす不届き者が後を絶たないので、制約項を追加します。

\mathbf{u}^TS\mathbf{u}+\lambda (1-\mathbf{u}^T\mathbf{u})

$\lambda$は係数(ラグランジュ乗数）です。この式を$\mathbf{u}$について偏微分して、0となる場所を探します。

S\mathbf{u}-\lambda \mathbf{u}=0\\
S\mathbf{u}=\lambda \mathbf{u}

なんとこの形はこの記事のいっちばん上で記した固有値問題の式$A\mathbf{x}=\lambda \mathbf{x}$と一致しています。つまり$\lambda$は固有値となるわけです。おおんすごいん

$S\mathbf{u}=\lambda \mathbf{u}$ に左から$\mathbf{u}^T$をかけると

$$
\mathbf{u}^TS\mathbf{u}=\lambda \mathbf{u}^T\mathbf{u}
$$

$\mathbf{u}^T\mathbf{u}=1$なので

$$
\mathbf{u}^TS\mathbf{u}=\lambda
$$

となり、分散が最大となるには、共分散行列の固有値から一番大きいものを選び、それに対応する固有ベクトルで射影すればよいということがわかりました。また、2次元、3次元へと射影するためには共分散行列の固有値の大きいものから順にそれに対応する固有ベクトルを選んでいけば良いです。固有値問題すげえ。

例えばデータが4次元の場合だと固有値は4つ出てきます。2次元に可視化するためには固有値が大きい順から二つを主成分とし、その固有値に対応した固有ベクトルによってデータを射影するのです。

実際に体感するために、具体的な実装例を以下に載せます。

print(__doc__)

#PCA：主成分分析
# Code source: Gaël Varoquaux
# License: BSD 3 clause

import numpy as np#numpyをインストール
import matplotlib.pyplot as plt#グラフを書くやつ
from mpl_toolkits.mplot3d import Axes3D#3次元plotを行うためのツール
from sklearn import decomposition#PCAのライブラリ
from sklearn import datasets#datasetsを取ってくる

n_component=2
np.set_printoptions(suppress=True)
fig = plt.figure(2, figsize=(14, 6))
iris = datasets.load_iris()
X = iris.data
y = iris.target
for i in range(4):#各データの平均を元のデータから引いている
    mean = np.mean(X[:,i])
    X[:,i]=(X[:,i]-mean)
X_cov=np.dot(X.T,X)#共分散行列を生成
w,v=np.linalg.eig(X_cov)#共分散行列の固有値、固有ベクトルを算出(固有値は既に大きさ順に並べられている)
for i in range(n_component):#固有値の大きい順に固有ベクトルを取り出す
    Xpc[i]=v[:,i]
Xpc=np.array(Xpc)
Xafter=np.dot(X,Xpc.T)#取り出した固有ベクトルでデータを線形写像する


pca = decomposition.PCA(n_components=2)
pca.fit(X)
Xlib = pca.transform(X)    


ax1 = fig.add_subplot(121)
for label in np.unique(y):
    ax1.scatter(Xlib[y == label, 0],
                Xlib[y == label, 1])
ax1.set_title('library pca')
ax1.set_xlabel("X_axis")
ax1.set_ylabel("Y_axis")
ax2 = fig.add_subplot(122)
for label in np.unique(y):
    ax2.scatter(Xafter[y == label, 0],
                Xafter[y == label, 1])
ax2.set_title('original pca')
ax2.set_xlabel("X_axis")
ax2.set_ylabel("Y_axis")
plt.show()

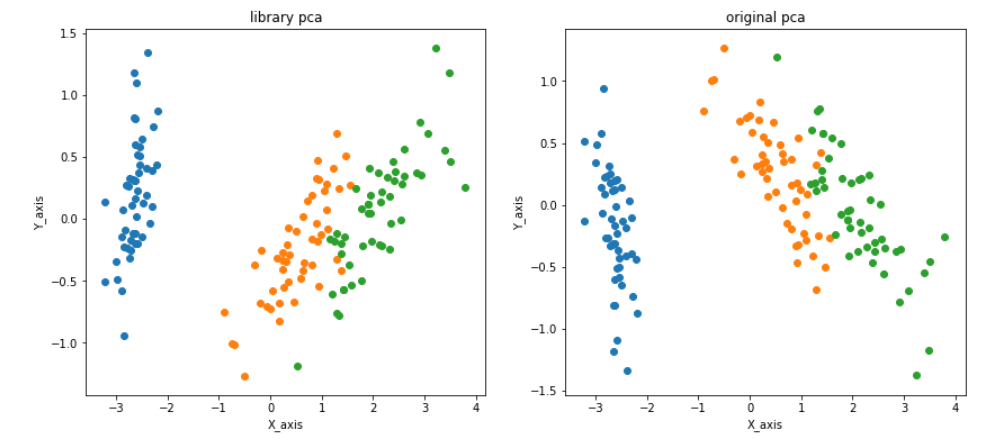
今回はScikit-learnに公開されているIrisデータセットという4次元のデータを2次元まで次元削減して可視化しています。
左はscikit-learnで公開されている主成分分析用のライブラリを使った結果、右は数式を実際に再現して主成分分析をした結果を示しています。
右と左で結果が違ってしまっているのは、scikit-learnのライブラリの仕様によるものです。普通固有ベクトルは一意に定まらない（向きが変わる）のですが、scikit-learnでは第1主成分とした固有ベクトルの第1要素が正となるように固有ベクトルを定めているため、結果が反転したりします。
Irisデータセットはアヤメの品種のデータセットです。セトナ、バーシクル、 バージニカという3種類のアヤメのがく片長,がく片幅,花びら長,花びら幅から構成されています。
Irisデータセットをそのまま図示しようとしても各アヤメのデータは4つあるため、2次元や3次元には図示できません。
そこで次元削減を行うのですが、出来るだけ情報を残して次元を落としたいものです。
主成分分析をした結果を見てみると、セトナ、バーシクル、 バージニカの3種類のデータが綺麗に分けられているように見えます。
これが分散の大きい軸を選ぶ利点です。分散の大きい軸を選ぶことで、データの情報を残したまま次元削減しているのです。
そしてそれを可能にしているのが固有値、固有ベクトルという要素なのです。

まとめ

本記事では固有値問題の一例として主成分分析を実装しました。
それにより、固有値、固有ベクトルが機械学習においても大事な要素であることがわかりました。

3本の記事に渡って固有値、固有ベクトルについて記述しましたが、3本通して読むことで固有値、固有ベクトルとは何か、どのように使われているのかを理解していただければ幸いです。
前編:固有値と固有ベクトルの性質
中編:固有値と固有ベクトルの応用例(二次形式)
後編:固有値と固有ベクトルの応用例(主成分分析)←今ここ

参考文献:ゼロから学ぶ線形代数、機械学習のエッセンス、パターン認識と機械学習(下巻)