GPTのモデルで文章生成する時に使う temperature というパラメータについて、色々調べてみました。
本稿ではGPT-2の日本語モデルを用いてhuggingface/transformersのgenerateメソッドに登場するtemperatureについて述べていきますが、transformersではなくOpenAIのAPI経由でGPT-3やChatGPTを使うときなどに指定できる同名のパラメータも同様の意味を持っていると思います。
環境
- Google Colab
- Python 3.8.16
- transformers 4.25.1
予めGoogle Colabで !pip install transformers sentencepiece しておきます。
準備
まずは準備としてtemperatureを指定せずに、普通に文章生成してみます。
import torch
from transformers import T5Tokenizer, AutoModelForCausalLM
MODEL_NAME = 'rinna/japanese-gpt2-xsmall' # 任意のモデルに変更
tokenizer = T5Tokenizer.from_pretrained(MODEL_NAME)
model = AutoModelForCausalLM.from_pretrained(MODEL_NAME)
with torch.no_grad():
input_ids = tokenizer.encode(
"昔々あるところに、おじいさんと",
add_special_tokens=False,
return_tensors="pt"
).to(model.device)
output_ids = model.generate(
input_ids,
max_length=20,
do_sample=True,
pad_token_id=tokenizer.pad_token_id
)
print(tokenizer.decode(output_ids.tolist()[0]))
昔々あるところに、おじいさんとおばあさんが、一緒に住んでいた。
"昔々あるところに、おじいさんと" という入力に対して、おばあさんが、一緒に住んでいた。というそれらしい続きが出力されました。この出力は毎回変わります。
これからtemperatureというパラメータについて、レベル1~レベル3の段階に分けて徐々に調べていきます。
レベル1: とりあえずtemperatureを指定してみる
temperatureが何なのか調べる前に、とりあえず指定したらどうなるのか見てみます。
generate()メソッドの引数にtemperatureを指定できます。float型で、0より大きい値を指定する必要があります。
output_ids = model.generate(
input_ids,
+ temperature=1.0,
max_length=20,
do_sample=True,
pad_token_id=tokenizer.pad_token_id
)
temperatureを0.01から5.0まで変化させながら、各3回ずつ出力してみます。
with torch.no_grad():
input_ids = tokenizer.encode(
"昔々あるところに、おじいさんと",
add_special_tokens=False,
return_tensors="pt"
).to(model.device)
for t in [0.01, 1.0, 2.0, 3.0, 4.0, 5.0]:
print("temperature:", t)
for _ in range(3):
output_ids = model.generate(
input_ids,
temperature=t,
max_length=20,
do_sample=True,
pad_token_id=tokenizer.pad_token_id
)
print(tokenizer.decode(output_ids.tolist()[0]))
以下のような結果が得られました。
temperature: 0.01
昔々あるところに、おじいさんとおばあさんが住んでいた。 昔は
昔々あるところに、おじいさんとおばあさんが住んでいた。 昔は
昔々あるところに、おじいさんとおばあさんが住んでいた。 昔は
temperature: 1.0
昔々あるところに、おじいさんとおばあさんが住んでいたという光景は忘れられ
昔々あるところに、おじいさんとおばあさんが集まって、この歌を
昔々あるところに、おじいさんとおばあさんの葬儀があると聞いたときは
temperature: 2.0
昔々あるところに、おじいさんとわたしの家から遠くの海を見る景色
昔々あるところに、おじいさんとおばさんたちがいて(その人が昔の
昔々あるところに、おじいさんと私の家族の墓が出来ているそうです。今
temperature: 3.0
昔々あるところに、おじいさんと一丸になり手土産もゲットしたりでき
昔々あるところに、おじいさんと年収1000組くらいのお婆さのお
昔々あるところに、おじいさんと子どもたちが住むおうちに子どもが入り住みつけ
temperature: 4.0
昔々あるところに、おじいさんとおば婆がおりたらきもしますっと
昔々あるところに、おじいさんと小学生3人が大勢現れ、 でも
昔々あるところに、おじいさんとおば婆も現れた。 また、「自分の
temperature: 5.0
昔々あるところに、おじいさんと弟夫婦や祖母などの親子のような顔して
昔々あるところに、おじいさんとご年男の方はいなかったのかもと思う。
昔々あるところに、おじいさんとおばぁは遊び相手ができてきた・そう
"昔々あるところに、おじいさんと"までが入力です。何度も生成したときの変化の仕方にtemperatureが影響しており、どうやら乱数や確率にかかわるパラメータらしいという事が分かります。
temperature=1.0までは、何度生成してもおばあさんで続きます。temperatureが低いほど何度生成しても一貫性のある出力が得られています。一方で、高くなるほど多様な出力が得られています。
実際にHuggingFace Transformersの公式ドキュメントにも、「The value used to module the next token probabilities.」とのことで、なんか確率にまつわる値である事は分かります。また、指定しなかったときはデフォルト値1.0が使われるようです。
レベル1まとめ: temperatureを上げるほど、多様な出力が得られる。
GPT-3による例
先述の例はGPT-2を使いましたが、OpenAI APIを通じてGPT-3でも同様にtemperatureを変化させながら出力を確認してみます。
モデルはtext-curie-001を用いています。
temperature=0.0だと、毎回同じ出力が得られました。
temperatureを上げるとおばあさんではなく「お母さん」が登場するなど、GPT-3の時と同様temperatureを上げると出力がより多様になりました。
ChatGPTによる例
同様に、ChatGPTでも3回ずつ生成してみます。モデルはchatgpt-3.5-turboを用います。
あまり変化が大きくはないものの、temperatureを上げると多様な出力が得られている事は分かります。
レベル2: temperatureの値による変化を調べる
temperatureはどうやら確率に影響するらしいという事が分かりました。実際に確率がどのように変化しているかを見てみます。
そのために、まずモデルが文章を出力する時に使っている確率分布を取り出してみます。generateメソッドの内部を参考にすると、モデルの出力するlogitsにsoftmaxを掛けたものを確率分布として扱っているようです。1この確率分布を取り出してみます。
input_ids = tokenizer.encode(
"昔々あるところに、おじいさんと",
add_special_tokens=False,
return_tensors="pt"
).to(model.device)
with torch.no_grad():
output = model(input_ids)
next_token_logits = output.logits[0, -1, :]
next_token_probs = torch.softmax(next_token_logits, dim=-1)
sorted_ids = torch.argsort(next_token_probs, descending=True, dim=-1)
for i in range(5):
print(f"{tokenizer.decode(sorted_ids[i])} ({100*next_token_probs[sorted_ids[i]]:.2f}%)")
おば (88.28%)
娘 (0.42%)
おじさん (0.40%)
、 (0.33%)
老人 (0.29%)
この確率分布において"昔々あるところに、おじいさんと"に続くトークンとして選ばれる確率が最も高いのは"おば"で、88.28%で圧倒的1位となっていました。他にも2位には"娘"、3位は"おじさん"などが続く確率が高いようです。人をあらわす言葉が続く確率が高いというのをうまく表現しているようです。不思議ですね。
入力に続くトークンの上位が、どれくらいの確率なのかが確認できました。これをtemperatureを変化させたときにどうなるか確認してみます。temperatureはlogits_warperにセットして扱っているので、logits_warperを変化させるように実装してみます。
import pandas
input_ids = tokenizer.encode(
"昔々あるところに、おじいさんと",
add_special_tokens=False,
return_tensors="pt"
).to(model.device)
prob_data = []
with torch.no_grad():
for t in [0.01, 1.0, 2.0, 3.0, 4.0, 5.0]:
output = model(input_ids)
next_token_logits = output.logits[0, -1, :]
logits_warper = model._get_logits_warper(
temperature=t,
num_beams=0,
)
next_token_logits = logits_warper(input_ids, next_token_logits)
next_token_probs = torch.softmax(next_token_logits, dim=-1)
sorted_ids = torch.argsort(next_token_probs, descending=True, dim=-1)
prob_data.append({
"temperature": t,
**{ i: f"{tokenizer.decode(sorted_ids[i])} ({100*next_token_probs[sorted_ids[i]]:.2f}%)" for i in range(5) }
})
pandas.DataFrame(prob_data)
| index | temperature | 1位 | 2位 | 3位 | 4位 | 5位 |
|---|---|---|---|---|---|---|
| 0 | 0.01 | おば (100.00%) | アミン (0.00%) | 総司令官 (0.00%) | ワシントン州 (0.00%) | 同書 (0.00%) |
| 1 | 1.0 | おば (93.63%) | 娘 (0.45%) | おじさん (0.42%) | 、 (0.35%) | 老人 (0.31%) |
| 2 | 2.0 | おば (36.70%) | 娘 (2.54%) | おじさん (2.47%) | 、 (2.25%) | 老人 (2.10%) |
| 3 | 3.0 | おば (16.13%) | 娘 (2.72%) | おじさん (2.67%) | 、 (2.51%) | 老人 (2.40%) |
| 4 | 4.0 | おば (9.93%) | 娘 (2.61%) | おじさん (2.58%) | 、 (2.46%) | 老人 (2.38%) |
| 5 | 5.0 | おば (7.31%) | 娘 (2.51%) | おじさん (2.48%) | 、 (2.39%) | 老人 (2.33%) |
"昔々あるところに、おじいさんと"のすぐ次に続くトークン上位5個と、その確率を出力してみました。
temperature=0.01の結果は特殊で、おばが100.00%となっており、他のトークンはよく分からないものが0.00%で並んでいます。順番に並べることができない状態になったのでしょうか。
どのtemperatureでもおばの確率が最も高くなっていますが、その確率の値には違いがあります。temperatureが低いほど上位トークンに確率が偏るようになっており、temperatureが高くなるほど確率の差が緩やかになっています。
その結果、先ほど見たようにtemperatureが低いほど一貫性がある出力を、temperatureが高くなるほど多様な出力をするようになりました。
レベル2まとめ: temperatureを上げるほど、トークン同士の出現確率の差が緩やかになる。
レベル3: なぜtemperatureというのかを調べる
オライリー「機械学習エンジニアのためのTransformers」によると、トークンの確率分布は次の計算式で計算されているようです。$T$がtemperatureにあたります。
$$
P(y_t=w_i|y_{\lt t},\boldsymbol{x})
= \frac{\exp(z_{t,i}/T)}{\sum_{j=1}^{|V|} \exp(z_{t,j}/T)}
$$
これをPythonプログラムにすると以下のような感じです。
import math
def probs_exp_temperature(a, t):
m = sum([ math.exp(x/t) for x in a ])
return [ math.exp(x/t) / m for x in a ]
# %に整形して表示
prob_percents = lambda xs: ', '.join(f"{x*100:.2f}%" for x in xs)
print(prob_percents(probs_exp_temperature([1,2,3], 1.0)))
9.00%, 24.47%, 66.52%
[1,2,3]という、3つの要素の"重み"を表したリストを入力として、確率分布が得られました。
temperatureを変化させていくと以下のようになります。
for t in [0.5, 1.0, 2.0]:
print(f"temperature={t} |", prob_percents(probs_exp_temperature([1,2,3], t)))
temperature=0.5 | 1.59%, 11.73%, 86.68%
temperature=1.0 | 9.00%, 24.47%, 66.52%
temperature=2.0 | 18.63%, 30.72%, 50.65%
先程見たように、「temperatureが高くなるほど確率の差が緩やかになる」ような特徴を持つ分布が得られました。
ところで、同書にはこの式に対する注釈として「ボルツマン分布に酷似していることにお気づきでしょう」とあります。私は気づきませんでした。というかそもそも ボルツマン分布 とは何でしょうか。
また、ここまでtemperatureと言っていますが、temperatureという英単語は「温度」という意味です。熱いとか冷たいとかの「温度」が、確率分布とどういう関係があるのでしょうか。
このあたりの答えは、どうもプログラミングの世界には無いようです。
ボルツマン分布
ボルツマン分布とは物理学の用語で、気体分子などの古典的粒子がどの状態にどれくらいの確率で存在するかをあらわす分布です。Wikipediaより引用すると、ボルツマン分布は以下のような式になっています。
$$
P_i = \frac{ \exp(-\epsilon_i/(kT)) }{ \sum_{j=1}^{M} \exp(-\epsilon_j/(kT)) }
$$
確かにTransformersのトークンの確率分布と並べてみると、なんだか似たような形の式です。
| transformersの確率分布 | 物理学のボルツマン分布 |
|---|---|
| $$\frac{\exp(z_{t,i}/T)}{\sum_{j}\exp(z_{t,j}/T)}$$ | $$\frac{ \exp(-\epsilon_i/(kT)) }{ \sum_{j} \exp(-\epsilon_j/(kT)) }$$ |
ボルツマン分布において、
- $P_i$は、粒子が状態$i$にある確率
- $\epsilon_i$は、状態$i$のエネルギー(変数)
- $M$は、すべての状態(変数)
- $k$は、ボルツマン定数(定数)
- $T$は、絶対温度(変数)
となっているようです。
物理学的な説明は省きますが、本稿において重要になる「温度」については少し調べてみます。
絶対温度
気体というのは気体分子の集合からなっていて、気体分子は常に運動しています。気体の温度が高いほど気体分子の運動のスピードが速くなって(運動エネルギーが大きくなって)、圧力が大きくなります。密閉して分子数の増減が無いようにした空間で、ピストンのようなものを使って圧力を一定にした環境下では、気体の温度が高くなるほどピストンが押し出されて気体の体積が大きくなります。
圧力が一定のとき、気体の体積は温度に比例します。シャルルの法則です。
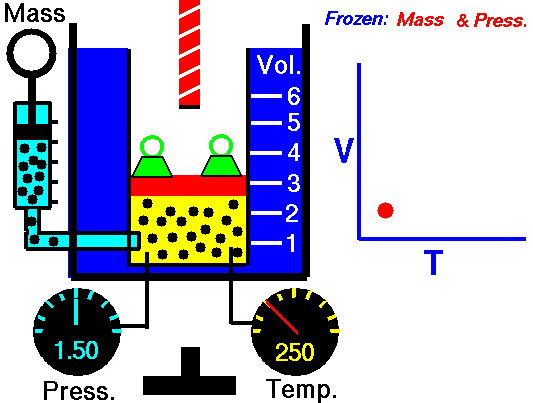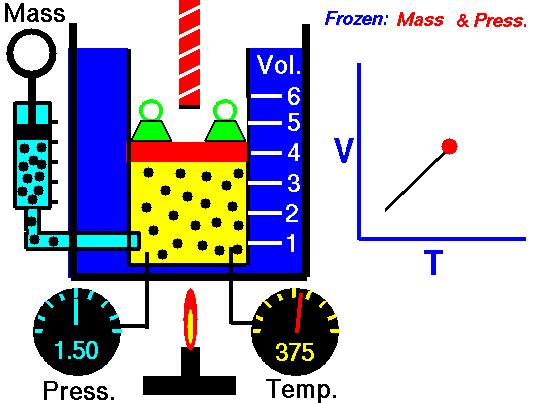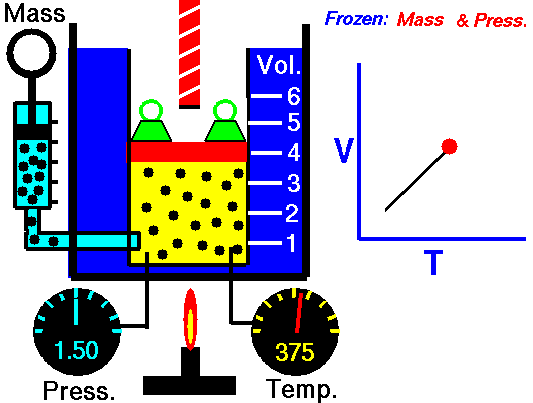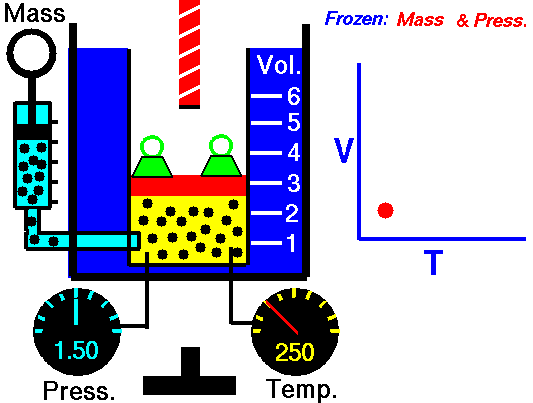
▲Charles's law - Wikipedia より引用
気体の体積が温度に比例するならば、温度が下がれば下がるほど体積が小さくなっていって、やがて体積がゼロになる点があります。この温度が絶対零度と呼ばれ、-273.15℃になります。-273.15℃を基準にした温度を絶対温度と呼びます。
我々が普段利用している「水が0℃で凍って、100℃で沸騰する」というときの温度はセルシウス温度と呼ばれます。セルシウス温度と絶対温度の関係は単純で、セルシウス温度から273.15を引いた値が絶対温度です。絶対温度の単位はケルビンKです。たとえば、日本の8月の平均気温2である約27℃が約300Kという感じです。
0K(-273.15℃)が絶対零度です。
ここまでが絶対温度の説明でした。さて、温度が高いほど気体分子の運動スピード(の平均値)が上がると言われても、気体中に分子はたくさん存在し、あっちこっちに向かって運動していています。どの"状態"にどれくらいの分子があるかはよく分かりません。
ボルツマン分布は気体分子が特定の状態に存在する確率をあらわしています。ボルツマン分布では、温度が低いほどエネルギーの小さい状態に分子が集まりやすい、という事を言っているようです。温度が最低の状態つまり絶対零度の状態では分子の運動が止まるので、分子は最もエネルギーの小さい状態に100%で固定されます。温度が上がるほど分子が激しく運動するようになっていくので、分子がどこにいるかという確率の差が緩やかになっていく、という感じのようです。
イメージとしては、温度が下がると固体(氷など)に近づくので一定箇所で固まって動かなくなるような感じ、温度が上がると固体から遠ざかるためその反対で自由に動きまくってどこに行ったか分からなくなる、という感じで掴んでいます。
(※これはあくまでイメージであり、ボルツマン分布の正しい説明ではありません)
確率分布を計算してみる
実際にボルツマン分布を計算してみましょう。
なおボルツマン分布における$k$は定数であり、本当はとてもとても小さい正の値です。しかしここでは物理学的な検証をするのではなく分布の特徴を確認したいだけなので、計算をしやすくするために$k=1$としてみます。
def boltzmann_distribution(a, t):
# K = 1.380649e-23 # 本来の値を代入すると、そのままでは計算できない
K = 1.0
m = sum([ math.exp(-x/(K*t)) for x in a ])
return [ math.exp(-x/(K*t)) / m for x in a ]
prob_percents(boltzmann_distribution([1,2,3], 1.0))
66.52%, 24.47%, 9.00%
これを、temperaruteの値を変えながら計算してみます。
for t in [0.5, 1.0, 2.0]:
print(f"temperature={t} |", prob_percents(boltzmann_distribution([1,2,3], t)))
temperature=0.5 | 86.68%, 11.73%, 1.59%
temperature=1.0 | 66.52%, 24.47%, 9.00%
temperature=2.0 | 50.65%, 30.72%, 18.63%
この結果はtransformersの分布の計算結果と似ています。横に並べてみます。
| temperature | transformersの分布 | 物理学のボルツマン分布 |
|---|---|---|
| 0.5 | 1.59%, 11.73%, 86.68% | 86.68%, 11.73%, 1.59% |
| 1.0 | 9.00%, 24.47%, 66.52% | 66.52%, 24.47%, 9.00% |
| 2.0 | 18.63%, 30.72%, 50.65% | 50.65%, 30.72%, 18.63% |
※transformersの分布とボルツマン分布との結果は鏡写しの関係になりましたが、実際のボルツマン分布とは$k$の値が異なるのでこの鏡写し関係は本質的なものではありません。
transformersの分布では入力の値が大きい値が確率が高くなりますが、ボルツマン分布ではエネルギーとして入力した値が大きいほど確率の値が低くなります。「temperatureの値が上がるほど、確率の差が緩やかになる」という傾向はいずれも同じです。
Softmax関数
さて「transformersの確率分布」として紹介した計算式$\frac{\exp(z_{t,i}/T)}{\sum_{j}\exp(z_{t,j}/T)}$は Softmax関数 と呼ばれるものです。実は本稿の途中で、文章生成中の内部の確率分布を取り出した時に一度登場していました。
a = torch.tensor([1.,2.,3.])
torch.softmax(a, dim=-1)
tensor([0.0900, 0.2447, 0.6652])
Softmax関数は入力を0から1までの間に正規化した確率分布に変換する性質を持ちます。分類問題において、どのクラスが何%の確率か、という分布を作ったりでき、ニューラルネットワークにおける活性化関数として使われます。
このSoftmax関数が物理学のボルツマン分布と類似した特徴を持つというのは、これまで見てきたとおりです。
実際にはボルツマン分布をもとにしたボルツマンマシンというものが提案され、ボルツマンマシンを機械学習等に応用したりされたようです。3世の中には賢い人がいますね。
ちなみに、Softmax関数と、$k=1$としたときのボルツマン分布とが、鏡写しの関係にあると述べました。このSoftmax関数と鏡写しの関数はSoftmin関数としてPyTorchに定義されています。
a = torch.tensor([1.,2.,3.])
torch.nn.functional.softmin(a, dim=-1)
tensor([0.6652, 0.2447, 0.0900])
まとめ
- temperatureが低いほど、確率の高いトークンの確率が高くなることで、一貫性のある生成が期待できる
- temperatureが高いほど、確率の低いトークンの確率が高くなることで、多様性のある生成が期待できる
参考
- How to generate text: using different decoding methods for language generation with Transformers
- O'Reilly Japan - 機械学習エンジニアのためのTransformers
- 『高校数学でわかるボルツマンの原理』(竹内 淳):ブルーバックス|講談社BOOK倶楽部
-
実際には、他のパラメータを指定しない単純なサンプリングモードになった時にこの確率分布どおりにトークンを選択する。decodingアルゴリズムにはtop-k samplingやbeam searchなどを組み合わせるため必ずしも確率分布だけを用いてその通りのトークンを選択するわけではない。 ↩
-
https://www.data.jma.go.jp/obd/stats/etrn/view/monthly_s1.php?prec_no=44&block_no=47662&year=2022&month=&day=&view= ↩














