TensorFlow.js学習メモ③ ロジスティック回帰(Logistic Regression)で車のエミッションの検査

はじめに

ロジスティック回帰モデルを使って車の燃費を予測してみました。
学習メモなので基本用語の詳しい解説などは書いていません。

前の記事は以下

前提知識

実装前に必要となる知識をまとめました。

ロジスティック回帰(Logistic Regression)

ロジスティック回帰は、ある事象が起こる確率を予測、分析したい時に用いられる手法です。
分類が曖昧なものを判別したいときに利用され、データが各クラスに所属する確率を計算することで分類を行います。
3種類以上の分類にも利用することができます。

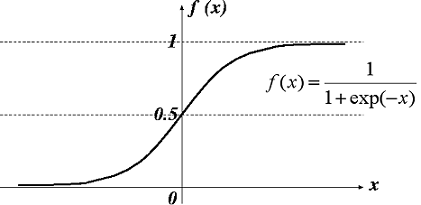
シグモイド関数

年齢によってどんな趣味を好む人が多いかどうかを判定したいケースを考えます。
10, 20歳は「映画」、30, 40, 50歳は「読書」が好みだとして、それぞれの趣味を0と1に数値化すると、Training dataのプロットは線形になりません。

このようなケースにフィットするのがシグモイド関数です。

交差エントロピー(Cross Entropy)

交差エントロピーはロジスティック回帰モデルの性能を数値化する手法の一つです。
線形回帰モデルの性能評価で使う平均二乗誤差(MSE)と同じ損失関数と呼ばれます。

式で表すと以下のようになります。
Actualは実測値をエンコードした値、Guessはsigmoid(mx+b)を示しています。

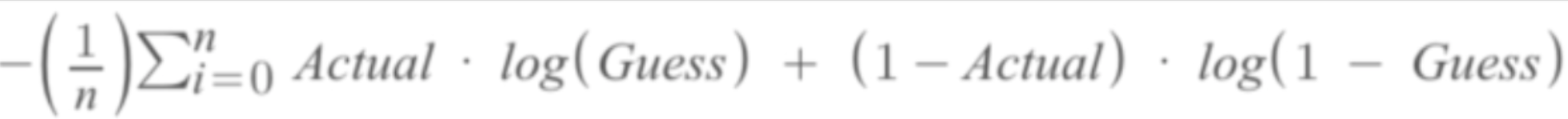
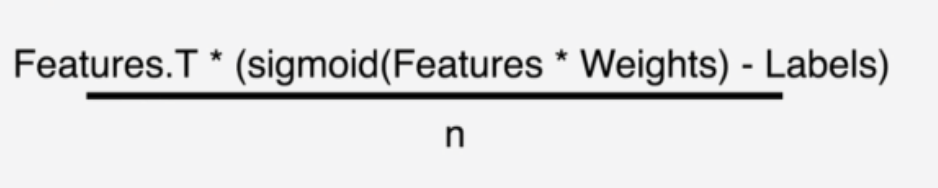
また、交差エントリーの微分は以下のように表すことができます。
weightsはm, bのテンソルになります。

実装

ロジスティック回帰モデルのクラスをつくるにあたり、線形回帰モデルのクラスをリファクタリングしました。

メソッドの構成

線形回帰モデルのクラスとメソッドの構成はほぼ同じですが、MSEではなくCross Entropyを算出するため、処理の内容が若干異なります。

コード

コードは以下です。

logistic-regression.js

const tf = require('@tensorflow/tfjs');
const _ = require('lodash');

class LogisticRegression {
  constructor(features, labels, options) {
    this.features = this.processFeatures(features);
    this.labels = tf.tensor(labels);
    this.costHistory = [];

    this.options = Object.assign(
      { learningRate: 0.1, iterations: 100, decisionBoundary: 0.5 },
      options
    );

    this.weights = tf.zeros([this.features.shape[1], 1]); //m, bの初期値
  }

  gradientDescent(features, labels) {
    const currentGuesses = features.matMul(this.weights).sigmoid();
    const differences = currentGuesses.sub(labels);

    const slopes = features
      .transpose()
      .matMul(differences)
      .div(features.shape[0]); //列の個数で割る

    this.weights = this.weights.sub(slopes.mul(this.options.learningRate));
  }

  train() {
    const batchQuantity = Math.floor(
      this.features.shape[0] / this.options.batchSize
    ); //バッチの回数

    for (let i = 0; i < this.options.iterations; i++) {
      for (let j = 0; j < batchQuantity; j++) {
        const startIndex = j * this.options.batchSize;
        const { batchSize } = this.options;

        const featureSlice = this.features.slice(
          [startIndex, 0],
          [batchSize, -1]
        );

        const labelSlice = this.labels.slice([startIndex, 0], [batchSize, -1]);

        this.gradientDescent(featureSlice, labelSlice);
      }

      this.recordCost();
      this.updateLearningRate();
    }
  }

  predict(observations) {
    return this.processFeatures(observations)
      .matMul(this.weights)
      .sigmoid()
      .greater(this.options.decisionBoundary) //指定値以上なら1
      .cast('float32');
  }

  //決定係数を出す
  test(testFeatures, testLabels) {
    const predictions = this.predict(testFeatures); //0.5以上は1にする
    testLabels = tf.tensor(testLabels);

    const incorrect = predictions.sub(testLabels).abs().sum().get(); //predictと一致しないカラムの数の合計

    return (predictions.shape[0] - incorrect) / predictions.shape[0]; //予想と一致した割合
  }

  processFeatures(features) {
    features = tf.tensor(features);
    features = tf.ones([features.shape[0], 1]).concat(features, 1);

    if (this.mean && this.variance) {
      features = features.sub(this.mean).div(this.variance.pow(0.5));
    } else {
      features = this.standardize(features);
    }

    return features;
  }

  standardize(features) {
    const { mean, variance } = tf.moments(features, 0);

    this.mean = mean;
    this.variance = variance;

    return features.sub(mean).div(variance.pow(0.5));
  }

  //Learning Rate調整のためにCostを記録する
  recordCost() {
    const guesses = this.features.matMul(this.weights).sigmoid();

    const termOne = this.labels.transpose().matMul(guesses.log());

    const termTwo = this.labels
      .mul(-1)
      .add(1)
      .transpose()
      .matMul(guesses.mul(-1).add(1).log());

    const cost = termOne
      .add(termTwo)
      .div(this.features.shape[0])
      .mul(-1)
      .get(0, 0);

    this.costHistory.unshift(cost);
  }

  //Learnin Rateの更新
  updateLearningRate() {
    if (this.costHistory.length < 2) {
      return;
    }

    if (this.costHistory[0] > this.costHistory[1]) {
      this.options.learningRate /= 2;
    } else {
      this.options.learningRate *= 1.05;
    }
  }
}

module.exports = LogisticRegression;

予測値の算出

入力値と算出したweights(m, b)をシグモイド関数に当てはめた結果が、入力したしきい値より大きければ1、小さければ0とします。
ロジスティック回帰における予測値はこのように算出されます。

  predict(observations) {
    return this.processFeatures(observations)
      .matMul(this.weights)
      .sigmoid()
      .greater(this.options.decisionBoundary) //指定値以上なら1
      .cast('float32');
  }

おわりに

3記事書いたことで学習内容を整理することができました。
今後の学習の指針については、AIに詳しい人にきいて考えてみようと思います。

参考資料