一様分布、正規分布、指数分布、ポアソン分布の乱数を生成する方法 (Scala)

乱数を生成するサンプルコードです。一様分布の乱数から特定の分布に従う乱数を生成する方法のメモです。

サンプルコードの言語はScalaです。

一様分布

一様分布の乱数を生成するRandomクラスをそのまま使います。

import scala.util.Random;

// 0からwidthまでの一様な分布の乱数
def randomUniform(width: Double, size: Int): IndexedSeq[Double] = (0 until size).map { _ =>
  width * Random.nextDouble();
}

正規分布

正規分布の乱数を一様分布の乱数から生成します。2個ずつ生成できるので、ループの回数を半分にしています。

import scala.util.Random;

// 平均mu、標準偏差sigmaの正規分布に従う乱数
def randomNormal(mu: Double, sigma: Double, size: Int): IndexedSeq[Double] = {
  val pi2 = 2 * Math.PI;
  (0 until (size + 1) / 2).flatMap { _ =>
    val rnd_a = Random.nextDouble();
    val rnd_b = Random.nextDouble();
    val rnd_a2 = Math.sqrt(-2 * Math.log(rnd_a));
    val rnd_b2 = pi2 * rnd_b;
    val random_1 = mu + sigma * rnd_a2 * Math.sin(rnd_b2);
    val random_2 = mu + sigma * rnd_a2 * Math.cos(rnd_b2);
    List(random_1, random_2);
  }.take(size);
}

2つの0～1の乱数から2つの正規分布の乱数を生成する式です。

\begin{align}
r_1 =& \sqrt{-2\log{a}} \sin{2\pi b} \\
r_2 =& \sqrt{-2\log{a}} \cos{2\pi b} \\
\end{align}

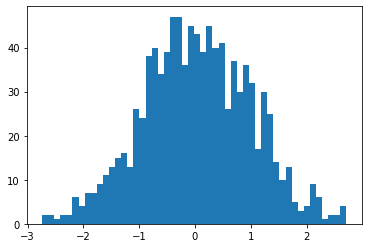
1000個作ったときのヒストグラム。

※Scalaであれば、Random.nextGaussian()というメソッドを使えます。この記事は一様分布から他の分布を生成する方法です。

指数分布

指数分布の乱数を一様分布の乱数から生成します。パラメータとしてlambdaが必要です。

import scala.util.Random;

// 平均1.0/lambdaの指数分布に従う乱数
def randomExponential(lambda: Double, size: Int): IndexedSeq[Double] = {
  val lambda1 = -1.0 / lambda;
  (0 until size).map { _ =>
    val x = Random.nextDouble();
    lambda1 * Math.log(x);
  }
}

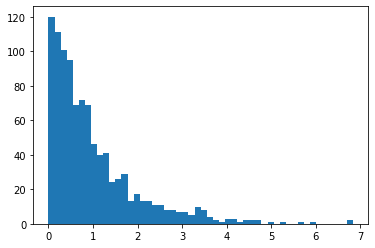
lambda=1.0で1000個作ったときのヒストグラム。

ポアソン分布

ポアソン分布の乱数を一様分布の乱数から生成します。パラメータとしてlambdaが必要です。ポアソン分布の乱数は0以上の整数です。

import scala.util.Random;

// 平均lambdaのポアソン分布に従う乱数
def randomPoisson(lambda: Double, size: Int): IndexedSeq[Int] = {
  val exp_lambda1 = Math.exp(-lambda);
  (0 until size).map { _ =>
    var r: Int = 0;
    var d: Double = Random.nextDouble();
    while (d >= exp_lambda1) {
      val x = Random.nextDouble();
      d = d * x;
      r = r + 1;
    }
    r;
  }
}

以上。