先日プログラミングコンテストの過去問を haskell でやった時に、べき乗をなんやかんやするロジックを書いた時に最終結果が12340000で欲しかったのに12340000.0になってしまって通りませんでした。恥ずかしい。
恥ずかしいけど、聞くは一時の恥聞かぬは一生の恥の解説とも言うし、知らないことは素直に学んで修めればなかったことにできるんです。できんの?
よくわからんけど、要するに曖昧なまま使ってたintみたいなものをきっちりまとめるぜって、そんな話。
かるーく背景
普段は java / DDD で契約管理のシステムを作ってるんだけど、扱う数字なんてたかだか数万の整数くらいなんだよね。ちょっとした円だとか契約の数を数えたりだとか、その程度。
なんと月の請求に日割りがないしね。驚きだね。
DDD の value object とかのおかげで、生のintとかを触ることもあんまりないしね。
なのでこの記事を書く直前の例えば java の理解度はだいたいこんな感じ。
「byte? よくわからんけど怖い」
「long? 長そ〜」
「BigInteger? でかそ〜」
「float? ふわふわ〜」
「double? 何が倍なの〜?とうおるるるるるるるる」
ってくらいの理解度。これ大マジ。
(double のイタリア語が doppio ってことだけは知ってたんだよォォォ)
なのでそれくらいの人がまとめたんだよってことだけ了承してね!
haskell 版もよろしく
この記事の確認言語には java を使っています。
もともと haskell で確認してたのですが、いくつかの言語を確認した方がより理解が進むかと思って java でも試してみました。
python でも少し確認したりしたのですが、記事は本懐の haskell と仕事で使ってる java にしようかと思います。
というわけで、こっちもよろしく。→ haskell の Int と Integer の違いや Float や Double や Rational を理解する
まずは概要
プログラミングに入る前に、数学の話です。
数学といっても代数とか圏論とかの怖いやつはでてこないです。僕も怖いので。
だいたいが中学校くらいまでの話。
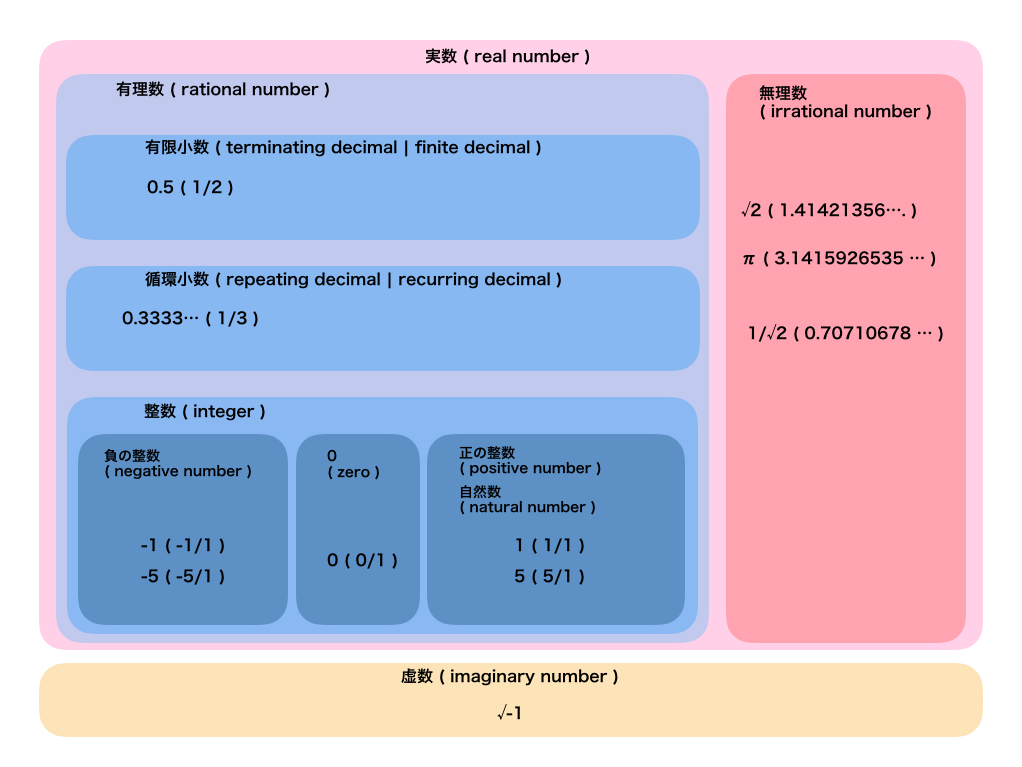
まずはこれを見てください。
ざっくり説明します。
実数と虚数
普段目にする数はだいたい実数です。
対して虚数は便利なので発明された数ですが、現実には存在しません。
代表的なのが√-1もしくはそれをiと表現したものですね。わかりやすいですね。僕はよくわかりません。
虚数は二乗して 0 未満の実数になる数で、実数はそれ以外と定義されます。
ここを細かく考える気はないので、「だいたい実数」くらいで大丈夫です。
有理数と無理数
実数の分類は真剣に考えます。
実数は有理数と無理数に大別されますが、有理数は整数の比で表現できる数です。
対してそれ以外の整数の比で表現できない数を無理数と言います。
整数と有限小数と循環小数
いずれも有理数です。
整数は説明するまでもありませんね。
3は3/1と表現できるので有理数です。
有限小数は0.5の様な終わりのある小数です。
1/2の様に整数の比で表現できます。
対して0.333...や0.142857142857142857...の様に同じ数字の繰り返しが無限に続く小数を循環小数と言います。
これも1/3や1/7の様に整数の比で表現できます。
負の整数と正の整数とゼロと自然数
整数は一番馴染みがあるのであまり問題ないと思いますが、一応。
負の整数は-1や-5のことで、-5/1の形で表現できます。
0は0/1ですね。
正の整数についても同様です。
また、正の整数を自然数とも言います。(0を含めるかは本記事では問いません)
小数と分数
少数と分数についての補足です。
分数は数の比で表現される数であり、一見有理数と同じな気がします。
が、有理数は整数の比なので、分数の方が広い概念です。
例えば1/√2なんてのもありです。これは整数の比ではないので無理数です。
(だいたい 0.7 なので二乗するとだいたい0.5で0より大きいので虚数ではないですね。)
また、例えば無限小数というものがありますが、先ほどの図で言うと、有理数の循環小数も無理数も無限小数です。
循環しているかしていないかの違いですね。
押さえておきたい英語
以上の要点を押さえつつ、我々プログラマは英単語も知らないと困るので、ざっくり整理しておきます。
(と言っても絵には英語も入ってますが。)
実数はreal numberで虚数はimaginary numberです、イメージつきやすいですね。
あまり馴染みはないですが、有理数はrational numberです。コピペで書いてると稀にぶち当たります。
ratioが比率という意味なので変数名で使ったことがある人もいるのではないでしょうか。
また、絵にはないですが小数はdecimalで分数はfractionです。
プログラミングの世界へ ( java )
さっそく java でサンプルコードを見たいところですが、人間の世界とコンピュータの世界では大きく違うことがあります。
それは「メモリが有限」ということです。
どこにそれが関係するかと言うと、例えば「すげーでけー数」と「無限小数」です。
固定長整数
例えば java のintは 32bit 固定の整数です。
コンピュータのメモリには限界があるので、数値を 32 の0|1の範囲に限定して表現します。
多倍長整数
対して多倍長整数は扱う数に応じて動的にメモリを確保する数値の表現方法です。
理論上は無限の数を扱うことができます。(もちろんコンピュータのメモリの許す限りですが。)
固定長整数と多倍長整数
みんな大好きオーバーフローはこの固定長整数が引き起こします。
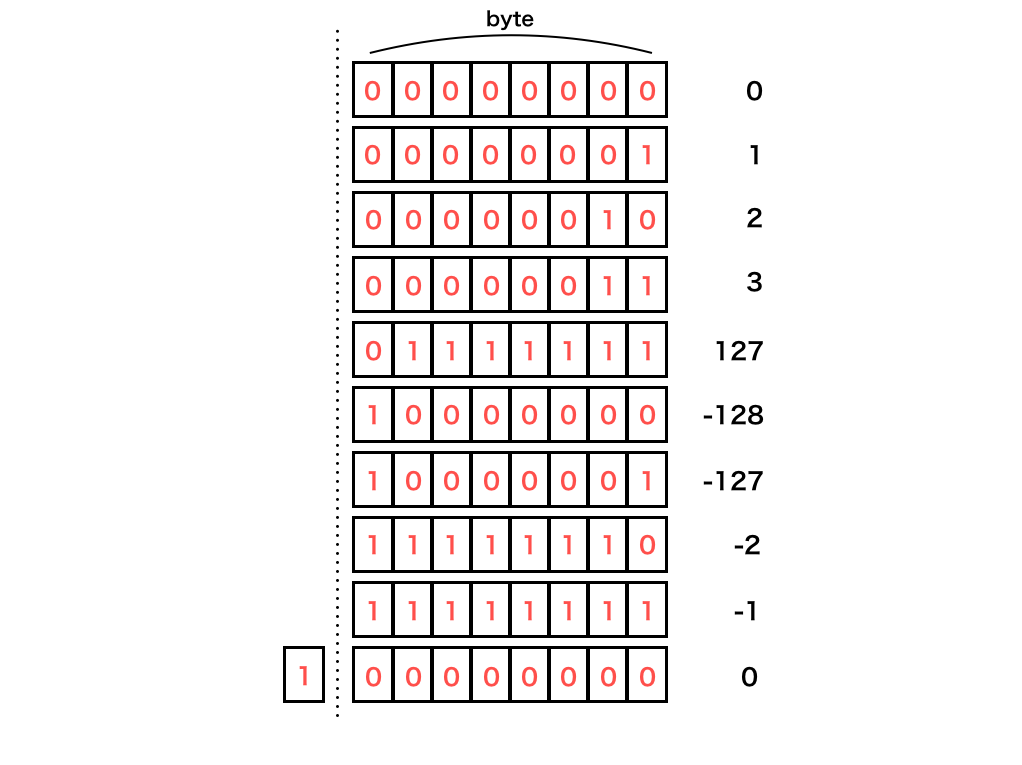
たとえば java のbyteは 8bit 固定の整数です。
頭の 1bit を正負の符号に、残りを値の表現に使います。
0000|0000から1ずつ増加を始め、0111|1111から1000|0000になるところでオーバーフローし、
1111|1111から1|0000|0000になるところで 9bit 目が範囲外になり0000|0000として扱われます。
(見やすくするために 4 桁ごとに|を入れています。)
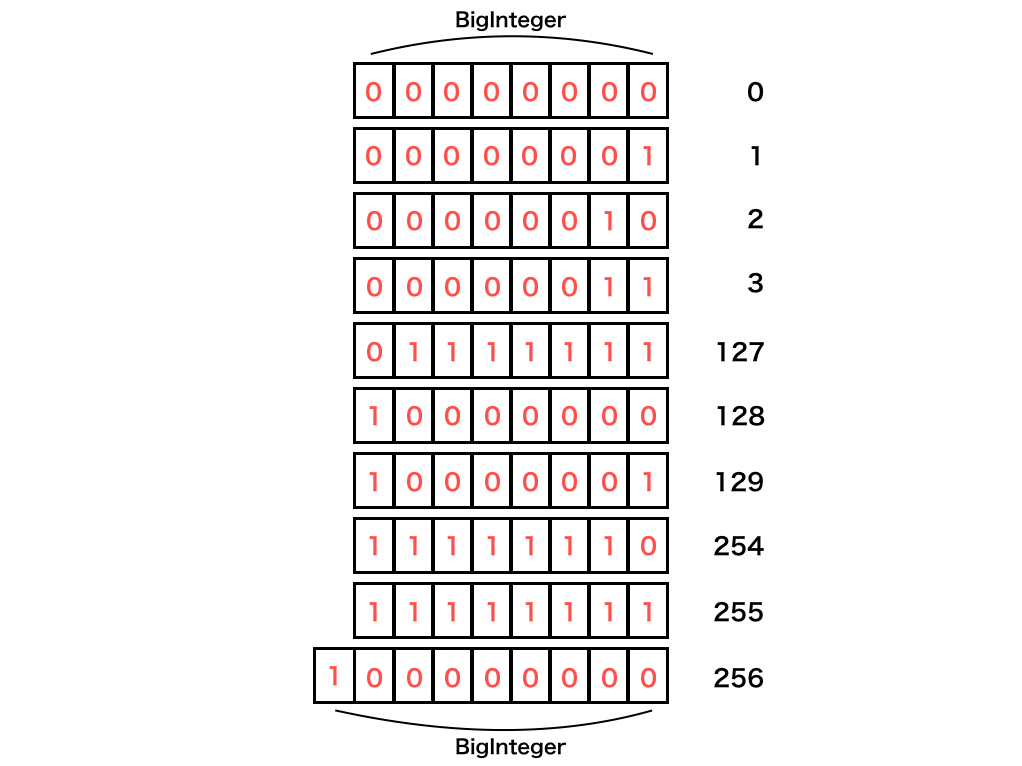
対してBigIntegerは多倍長整数です。
こいつは桁あふれが起きそうになると、動的にメモリを確保するのでオーバーフローしません。
(符号や値の保持については実装方法によるので、上図はイメージです。)
固定長整数はメモリ効率や性能に優れ、多倍長整数は精度に優れます。
これらは適材適所です。
浮動小数点
整数と同じく小数においても同様の考え方があります。
浮動小数点とは数値の表現方法の一つで、固定長の仮数部と指数部を持つ表現方法です。
ざっくり仮数部は値で指数部は桁を表していると考えれば大丈夫。
例えば二進数の0.00000101は101 * 2^-8の様に表されます。
ただこれだと10.1 * 2^-7とかでも表現できちゃうので、IEEE754と言う規格で仮数部は1.xにすると決まってます。なので1.01 * 2^-6です。
1.01e-6なんて書いたりもします。
コード書いていてたまに出るe入ってるやつはこれだね。怖かったけど克服したぞ。
仮数部と指数部によって小数点を打つ位置が変わってくるので浮動小数点と言うのかな。
一方で対になる単語は固定小数点で、例えば整数がこれに含まれます。
java で確認
前置きが長くなりました。ここからはガシガシ java で確認していきます。
| type | 説明 |
|---|---|
| byte, Byte | 8bit 固定長整数 |
| short, Short | 16bit 固定長整数 |
| int, Integer | 32bit 固定長整数 |
| long, Long | 64bit 固定長整数 |
| float, Float | 単精度浮動小数点 ( 32bit ) |
| double, Double | 倍精度浮動小数点 ( 64bit ) |
| BigInteger | 多倍長整数 |
| BigDeciaml | 多倍長小数 |
以下のコードはSystem.out.printlnに相当するものは省略し、その行のコメントがその結果とします。
byte, short, int, long
たくさんあるけど恐れることはありません。
こいつらは全部固定長整数で、違いは表現できる精度しかありません。
Byte.MAX_VALUE; // 127
Short.MAX_VALUE; // 32767
Integer.MAX_VALUE; // 2147483647
Long.MAX_VALUE; // 9223372036854775807
例えばIntegerの上限値に+1すると、オーバーフローします。
Integer.MAX_VALUE + 1; // -2147483648
相互変換
また当然ですが、精度の低い方から大きい方へのキャストは問題ありませんが、逆は正しく行えません。
short s = 20000;
(int) s; // 20000
int i = 40000;
(short) i; // -25536
ところで int と Integer の違い
もともとの趣旨とは離れるのですが、案外面白いのでせっかくと言うことで。
java のintはプリミティブ型で、Integerはクラス型と言います。
主な違いはすんごいざっくり言うと「intはnullが許容されない」のと、「intはList<T>とかのTになれない」くらいです。
精度とかについてはintとIntegerに違いはありません。これ大事。
また java にはコンパイラがよしなに相互変換してくれる仕組みがあるので、大体の場合はあんまりどちらかを気にしなくても大丈夫です。
相互変換、の前にメモリの話
普段あんまり考えることはないかもしれませんが、スタック領域とヒープ領域について超ざっくり説明します。
例えばこの様なコードを書いた場合。
(intとIntegerの変数を区別しやすくするため、本記事では変数名の先頭に大文字を使います。)
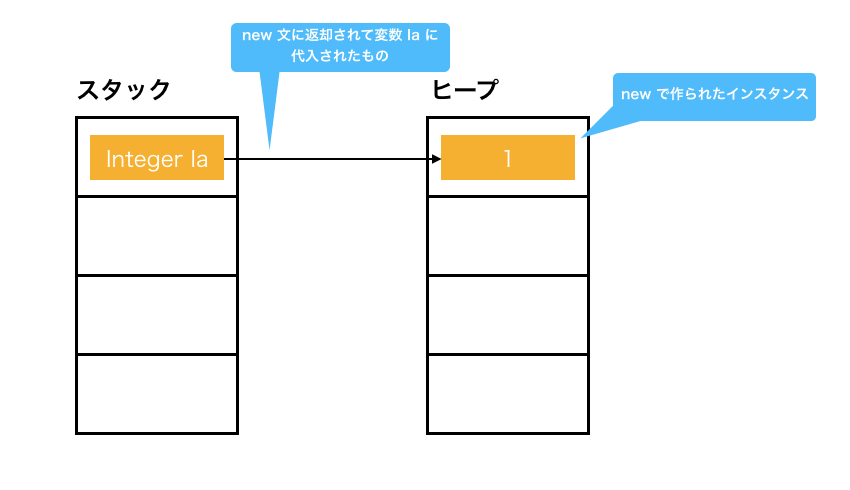
Integer Ia = new Integer(1);
この場合、メモリはこんな感じになってます。
newをするとスタック領域のIaという変数に何かが入ります。
なんとなくIaにはインスタンス自体が入ってる気がしますが、入ってるのは矢印だけです。恐ろしい言い方をするとポインタです。
作られたインスタンスはヒープ領域に入っています。
対してプリミティブ型のintはスタック領域にそのまま確保されます。
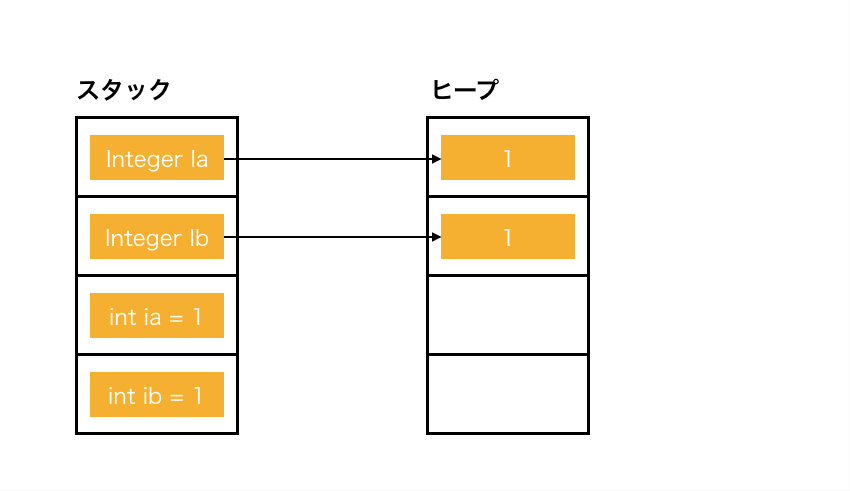
Integer Ia = new Integer(1);
Integer Ib = new Integer(1);
int ia = 1;
int ib = 1;
なのでこんなコードを書いた場合の絵は下のようになります。
同一性と同値性
「java で比較に==を使うんじゃあねぇ」と怖い人に怒られたことがある人はいっぱいいると思いますが、せっかくなのでなんでなのか見てみましょう。
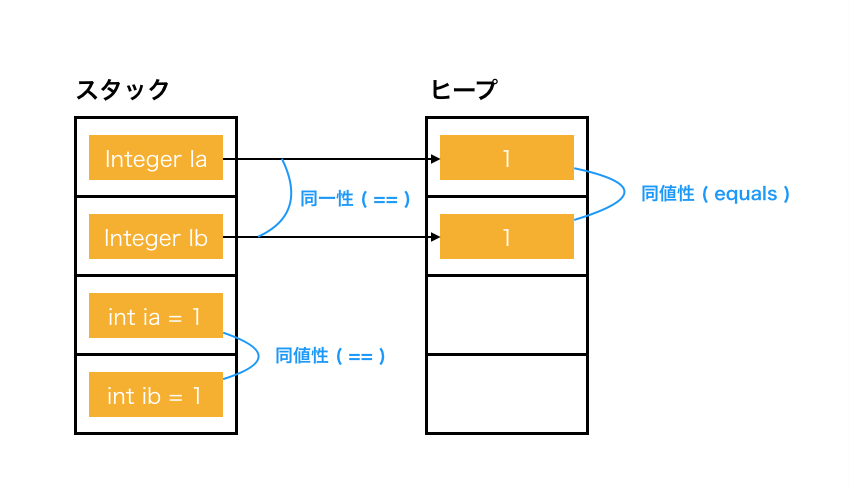
クラス型における同一性は同じインスタンスかを、同値性は同じ値かを比較することです。
前者は==で、後者はequalsによって行われます。また同値性は実装に依存します。
(例えば DDD の entity の比較では identity の一致のみで同値とみなす場合もあります。)
プリミティブ型の==はシンプルに値を比較します。
なのでIa == Ibは宛先の違う矢印なので false です。Ia.equals(Ib)は宛先の値が同じなので true です。
例えるなら「A さんも B さんも 500 円玉を持っていて、物理的には違う硬貨だけど価値は同じ」と言った感じです。
auto boxing と auto unboxing
スタック領域とヒープ領域、比較について理解したところで、相互変換についてです。
int -> Integerを boxing , 逆を unboxing と言います。
ラッパークラスの箱に入れるイメージかな。
以下のコードが実行できるのは auto boxing | auto unboxing によるものです。
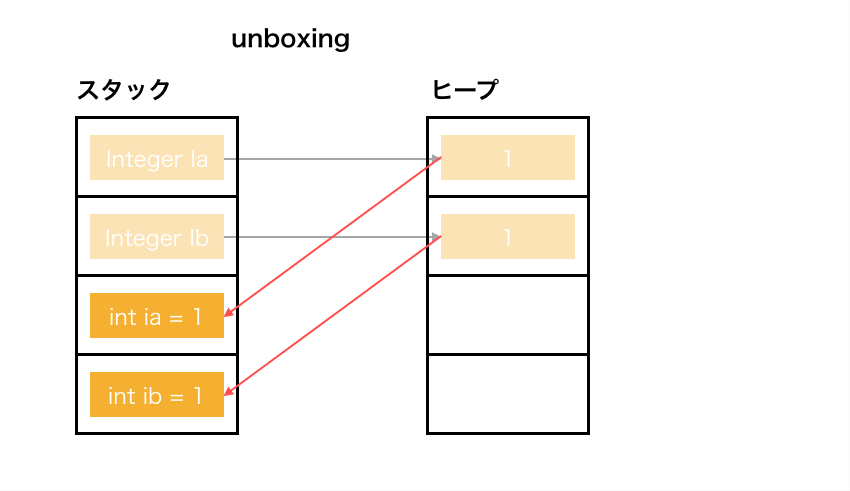
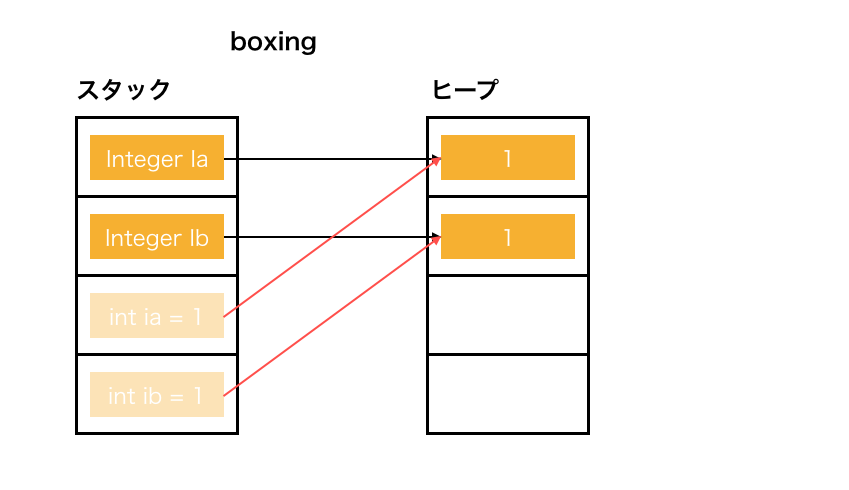
Integer Ia = new Integer(1);
int ia = Ia; // unboxing
int ib = 1;
Integer Ib = ib; // boxing
内部的にはスタック領域に値を持ってきたり、ヒープ領域にインスタンスを作って参照を得たりしています。
(実際には元の値は消えませんが、イメージしやすいので薄くしています。)
余談 落とし穴
さて、以下のコードはtrueとfalseどちらになるでしょうか。
int ia = 1;
int ib = 1;
Integer Ia = ia;
Integer Ib = ib;
Ia == Ib; // true or false ?
auto boxing によってnewされるのでIaとIbの矢印は違うはずです。上の絵でもそうなってます。
が、これtrueになります。
どうやら auto boxing はInteger#valueOfで、auto unboxing はInteger#intValueによって実現される様です。
Integer Ia = Integer.valueOf(ia);
Integer Ib = Integer.valueOf(ib);
で、肝心のInteger#valueOfですが、こんな実装になっています。
public static Integer valueOf(int i) {
if (i >= IntegerCache.low && i <= IntegerCache.high)
return IntegerCache.cache[i + (-IntegerCache.low)];
return new Integer(i);
}
どうやらよく使う-128~127はキャッシュされているみたいですね。なので上のコード例だとnewされないです。
こんなコードだとちゃんとfalseになります、理解は間違ってなかった様で安心だ。
int ia = 1000;
int ib = 1000;
Integer Ia = ia;
Integer Ib = ib;
Ia == Ib; // false
あ、ちなみに内部では auto unboxing にInteger#intValueを使うと言うことは、Iaがnullの場合に auto unboxing をするとNullPointerExceptionがでますよ。
int と Integer の違いまとめ
- 精度は同じ
- 比較はちょっと気をつけろよ
- 相互変換は便利だけど完全に置き換えてくれるわけではないから気をつけろよ
ってことですね。
本記事においては以後intとIntegerやfloatとFloatは精度の違いがないため、特に断りなくサンプルコードで都合が良い方を用います。
float, double
整数は押さえましたね。次は小数です。
doubleの何が倍なんだって思ってましたが、勉強すれば明瞭ですね。
floatは 32bit を使って、doubleは 64bit を使って値を表現するということでした。だから倍精度。
コンピュータのメモリが有限である以上無限小数を完全に表現することは不可能なので、誤差が出る前提で扱わなければなりません。
例えば十進数の0.01は二進数だと有限で表現することができません。
有限で表現できない以上どこかで諦めなければいけず、それを繰り返せば誤差が大きくなるのはなんとなく感覚で理解できますね。
で、どんな誤差が出るか、です。試してみましょう。
float f = 0;
for (int i = 0; i < 100; i++) {
f += 0.01f;
}
double d = 0;
for (int i = 0; i < 100; i++) {
d += 0.01d;
}
f; // 0.99999934
d; // 1.0000000000000007
doubleの方が1.0に近いですね。
相互変換
floatとdoubleの変換も、shortとintと同様に精度の高い方から低い方へ変換すると壊れます。
f; // 0.99999934
d; // 1.0000000000000007
(double) f; // 0.9999993443489075
(float) d; // 1.0
doubleからfloatにした場合は欠けてしまっていますね。
またそもそも有限なので、単純に以下の様な値で誤差が出ます。
10d / 3d; // 3.3333333333333335
1.00000001f; // 1.0
BigInteger, BigDecimal
お待たせしました、多倍長の奴らです。
こいつらは桁に応じて動的にメモリを確保するので、オーバーフローしないし誤差も出ません。なんかすごい。
さっそく試してみましょう。
BigDecimal
小数のBigDecimalから試してみます。初っ端から気前よく巨大な整数を扱ってみましょう。
BigDecimal bd = new BigDecimal(Long.MAX_VALUE);
bd; // 9223372036854775807
bd.add(new BigDecimal(1)); // 9223372036854775808
longの上限に加算してもオーバーフローしてません。
もっと思い切りよく足しても全然大丈夫。
bd.add(bd); // 18446744073709551614
小数も加算できる。
bd.add(new BigDecimal(0.5)); // 9223372036854775807.5
本命?の小数の誤差はどうでしょうか。
BigDecimal bd = BigDecimal.ZERO;
BigDecimal x = new BigDecimal(0.01);
for (int i = 0; i < 100; i++) {
bd = bd.add(x);
}
bd; // 1.00000000000000002081668171172168513294309377670288085937500
doubleの1.0000000000000007より精度が良いですね。(toString出来ているのはすげぇ頑張ってるからです。)
doubleで誤差が出た10d / 3dはどうでしょうか。
BigDecimal bd10 = new BigDecimal(10);
BigDecimal bd3 = new BigDecimal(3);
bd10.divide(bd3); // ArithmeticException: Non-terminating decimal expansion; no exact representable decimal result.
terminatingって単語は冒頭のベン図っぽいもので見ましたね、有限小数じゃあないって怒られてます。
誤差のでる値は誤差のあるまま持たせてくれないみたいですね。
切り捨てたり切り上げたりを明示しないとだめみたいです。
bd10.divide(bd3, RoundingMode.FLOOR) // 3
bd10.divide(bd3, RoundingMode.CEILING) // 4
BigInteger
こいつは簡単です。小数の扱えないBigDecimalです。
BigInteger bi = BigInteger.valueOf(Long.MAX_VALUE);
bi; // 9223372036854775807
bi.add(bi); // 18446744073709551614
BigIntegerには0.5みたいな小数を渡せる生成メソッドがないので、BigDecimalと比べると「これだけ」です。
もう大丈夫。怖くない。
余談 破壊/非破壊
ところでなんとなく java の感覚だとaddすると破壊する気がしませんか?
List#addとかそうじゃん。
けど、addするたびにメモリを確保し直す可能性があることを理解していると、非破壊で毎度違うインスタンスを作ってるって考えやすいよね。
(実装方法によるので immutable の場合もあるけど mutable の場合もあるらしい。)
まとめ
ながーい記事になったけど、やってみて感じた java における数値表現の要点は3つだけだ!
-
byte,short,int,longの違いは精度だけ、それぞれ限界があるぜ -
float,doubleも違いは精度だけ、小数は有限のメモリでは表現できないので誤差が前提なんだぜ -
BigIntegerとBigDecimalは(メモリがある限り)限界がない整数と小数だぜ
これだけだ!intとIntegerの違いは数値表現ってより java のお勉強としてがんばるんだ!
いやーそれにしても勉強になった。普段どれだけ適当にやってきたかを痛感した。
そしてこれを理解したらどうするかと言うと、やっぱドメインロジックとは切り離したいので value object を作って隠蔽するわけだ!
きっちり理解したので普段の業務(ドメイン実装)ではやっぱり使わないわけだ!なんというパラドクス!