先日プログラミングコンテストの過去問を haskell でやった時に、べき乗をなんやかんやするロジックを書いた時に最終結果が12340000で欲しかったのに12340000.0になってしまって通りませんでした。恥ずかしい。
恥ずかしいけど、聞くは一時の恥聞かぬは一生の恥の解説とも言うし、知らないことは素直に学んで修めればなかったことにできるんです。できんの?
よくわからんけど、要するに曖昧なまま使ってたIntみたいなものをきっちりまとめるぜって、そんな話。
かるーく背景
普段は java / DDD で契約管理のシステムを作ってるんだけど、扱う数字なんてたかだか数万の整数くらいなんだよね。ちょっとした円だとか契約の数を数えたりだとか、その程度。
なんと月の請求に日割りがないしね。驚きだね。
DDD の value object とかのおかげで、生のIntとかを触ることもあんまりないしね。
なのでこの記事を書く直前の例えば java の理解度はだいたいこんな感じ。
「byte? よくわからんけど怖い」
「long? 長そ〜」
「BigInteger? でかそ〜」
「float? ふわふわ〜」
「double? 何が倍なの〜?とうおるるるるるるるる」
ってくらいの理解度。これ大マジ。
(double のイタリア語が doppio ってことだけは知ってたんだよォォォ)
なのでそれくらいの人がまとめたんだよってことだけ了承してね!
java 版もよろしく
この記事の確認言語には haskell を使っています。
もともと haskell で確認してたのですが、いくつかの言語を確認した方がより理解が進むかと思って java でも試してみました。
python でも少し確認したりしたのですが、記事は本懐の haskell と仕事で使ってる java にしようかと思います。
というわけで、こっちもよろしく。→ java の int と Integer と BigInteger の違いや float や double を理解する
まずは概要
プログラミングに入る前に、数学の話です。
数学といっても代数とか圏論とかの怖いやつはでてこないです。僕も怖いので。
だいたいが中学校くらいまでの話。
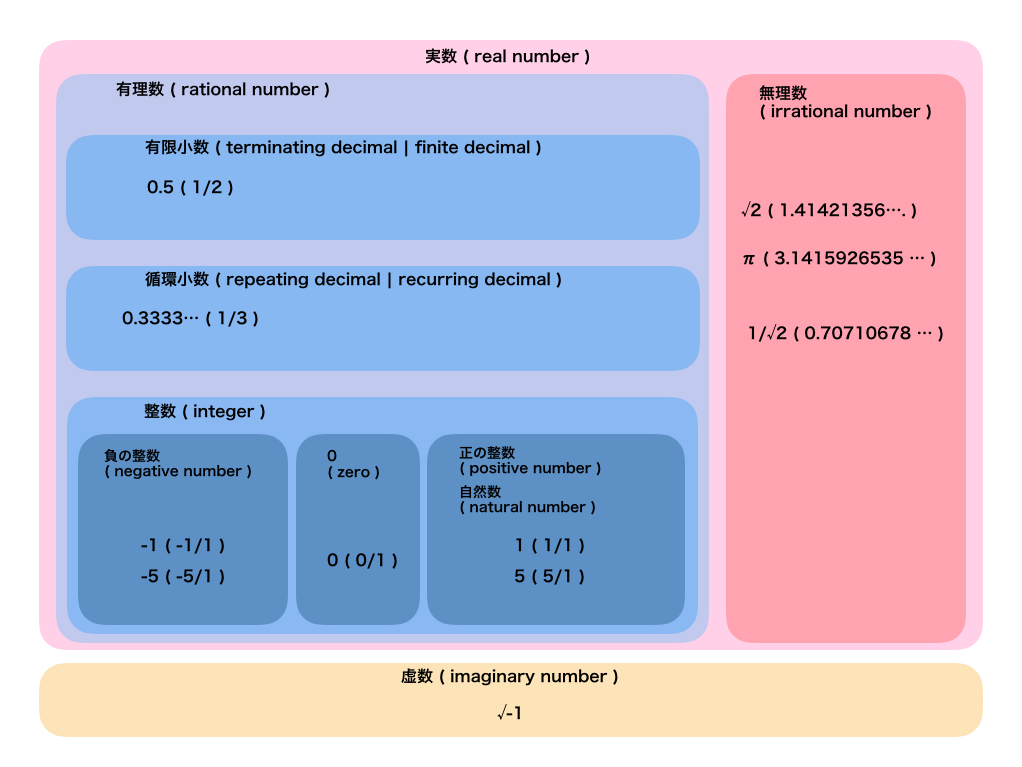
まずはこれを見てください。
ざっくり説明します。
実数と虚数
普段目にする数はだいたい実数です。
対して虚数は便利なので発明された数ですが、現実には存在しません。
代表的なのが√-1もしくはそれをiと表現したものですね。わかりやすいですね。僕はよくわかりません。
虚数は二乗して 0 未満の実数になる数で、実数はそれ以外と定義されます。
ここを細かく考える気はないので、「だいたい実数」くらいで大丈夫です。
有理数と無理数
実数の分類は真剣に考えます。
実数は有理数と無理数に大別されますが、有理数は整数の比で表現できる数です。
対してそれ以外の整数の比で表現できない数を無理数と言います。
整数と有限小数と循環小数
いずれも有理数です。
整数は説明するまでもありませんね。
3は3/1と表現できるので有理数です。
有限小数は0.5の様な終わりのある小数です。
1/2の様に整数の比で表現できます。
対して0.333...や0.142857142857142857...の様に同じ数字の繰り返しが無限に続く小数を循環小数と言います。
これも1/3や1/7の様に整数の比で表現できます。
負の整数と正の整数とゼロと自然数
整数は一番馴染みがあるのであまり問題ないと思いますが、一応。
負の整数は-1や-5のことで、-5/1の形で表現できます。
0は0/1ですね。
正の整数についても同様です。
また、正の整数を自然数とも言います。(0を含めるかは本記事では問いません)
小数と分数
少数と分数についての補足です。
分数は数の比で表現される数であり、一見有理数と同じな気がします。
が、有理数は整数の比なので、分数の方が広い概念です。
例えば1/√2なんてのもありです。これは整数の比ではないので無理数です。
(だいたい 0.7 なので二乗するとだいたい0.5で0より大きいので虚数ではないですね。)
また、例えば無限小数というものがありますが、先ほどの図で言うと、有理数の循環小数も無理数も無限小数です。
循環しているかしていないかの違いですね。
押さえておきたい英語
以上の要点を押さえつつ、我々プログラマは英単語も知らないと困るので、ざっくり整理しておきます。
(と言っても絵には英語も入ってますが。)
実数はreal numberで虚数はimaginary numberです、イメージつきやすいですね。
あまり馴染みはないですが、有理数はrational numberです。コピペで書いてると稀にぶち当たります。
ratioが比率という意味なので変数名で使ったことがある人もいるのではないでしょうか。
また、絵にはないですが小数はdecimalで分数はfractionです。
プログラミングの世界へ ( haskell )
さっそく haskell でサンプルコードを見たいところですが、人間の世界とコンピュータの世界では大きく違うことがあります。
それは「メモリが有限」ということです。
どこにそれが関係するかと言うと、例えば「すげーでけー数」と「無限小数」です。
固定長整数
例えば haskell のIntは僕の環境では 64bit 固定の整数です。
コンピュータのメモリには限界があるので、数値を 64 の0|1の範囲に限定して表現します。
多倍長整数
対して多倍長整数は扱う数に応じて動的にメモリを確保する数値の表現方法です。
理論上は無限の数を扱うことができます。(もちろんコンピュータのメモリの許す限りですが。)
固定長整数と多倍長整数
みんな大好きオーバーフローはこの固定長整数が引き起こします。
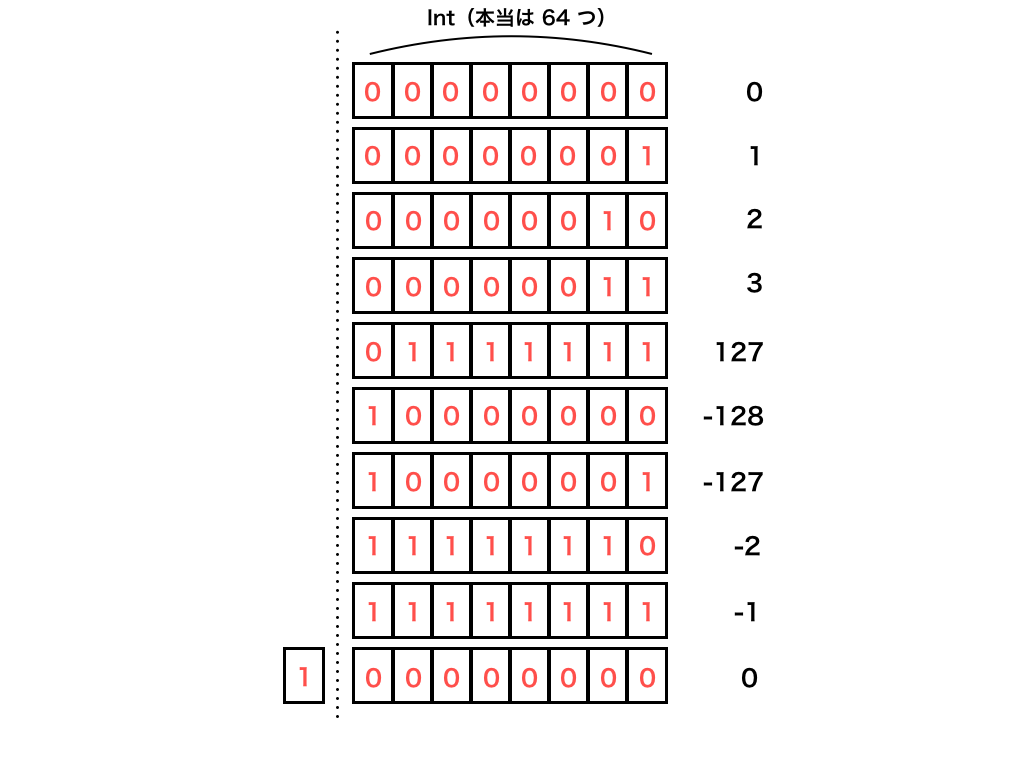
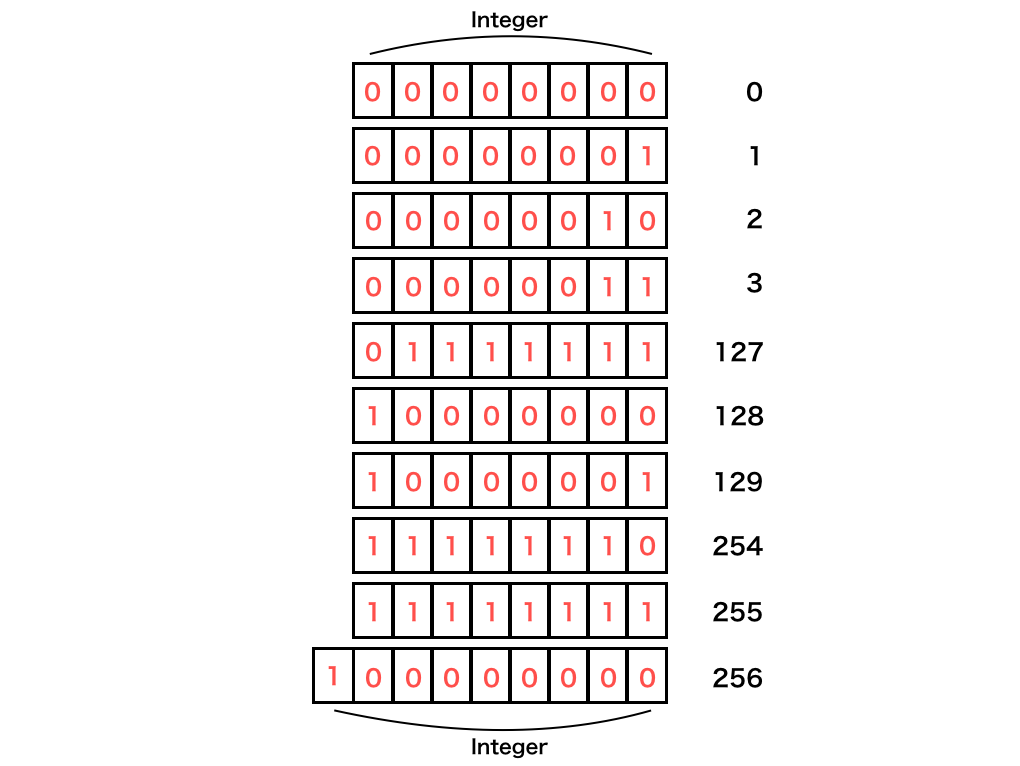
haskell のIntを 8bit 固定の整数だと仮定して考えます。
頭の 1bit を正負の符号に、残りを値の表現に使います。
0000|0000から1ずつ増加を始め、0111|1111から1000|0000になるところでオーバーフローし、
1111|1111から1|0000|0000になるところで 9bit 目が範囲外になり0000|0000として扱われます。
(見やすくするために 4 桁ごとに|を入れています。)
対してIntegerは多倍長整数です。
こいつは桁あふれが起きそうになると、動的にメモリを確保するのでオーバーフローしません。
(符号や値の保持については実装方法によるので、上図はイメージです。)
固定長整数はメモリ効率や性能に優れ、多倍長整数は精度に優れます。
これらは適材適所です。
浮動小数点
整数と同じく小数においても同様の考え方があります。
浮動小数点とは数値の表現方法の一つで、固定長の仮数部と指数部を持つ表現方法です。
ざっくり仮数部は値で指数部は桁を表していると考えれば大丈夫。
例えば二進数の0.00000101は101 * 2^-8の様に表されます。
ただこれだと10.1 * 2^-7とかでも表現できちゃうので、IEEE754と言う規格で仮数部は1.xにすると決まってます。なので1.01 * 2^-6です。
1.01e-6なんて書いたりもします。
コード書いていてたまに出るe入ってるやつはこれだね。怖かったけど克服したぞ。
仮数部と指数部によって小数点を打つ位置が変わってくるので浮動小数点と言うのかな。
一方で対になる単語は固定小数点で、例えば整数がこれに含まれます。
haskell で確認
前置きが長くなりました。ここからはガシガシ haskell で確認していきます。
| type | 説明 |
|---|---|
| Int | 64bit 固定長整数 |
| Integer | 多倍長整数 |
| Float | 単精度浮動小数点 ( 32bit ) |
| Double | 倍精度浮動小数点 ( 64bit ) |
以下のコードは repl の実行とその結果です。
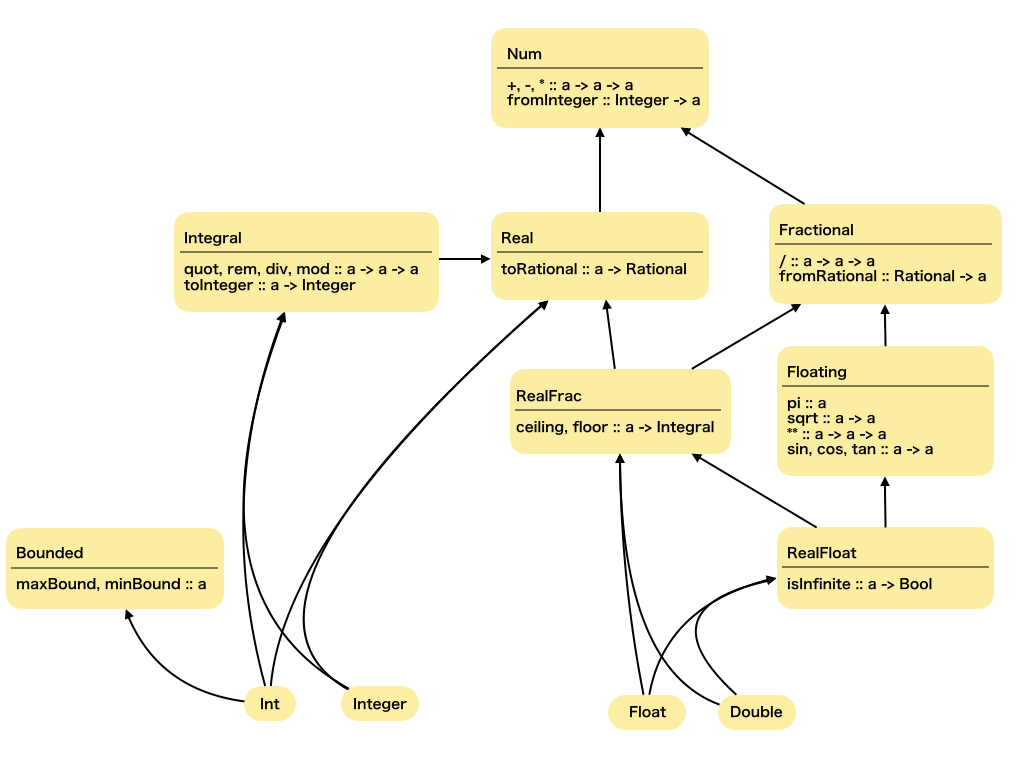
また、この絵は「なんとなく数値っぽい型とそこに定義されていた関数を整理した絵」です。
IntはIntegralクラスのインスタンスになっているのでInt -> Integralと線を入れています。
ghci> :info Int
data Int = GHC.Types.I# GHC.Prim.Int# -- Defined in ‘GHC.Types’
instance Eq Int -- Defined in ‘GHC.Classes’
instance Ord Int -- Defined in ‘GHC.Classes’
instance Show Int -- Defined in ‘GHC.Show’
instance Read Int -- Defined in ‘GHC.Read’
instance Enum Int -- Defined in ‘GHC.Enum’
instance Num Int -- Defined in ‘GHC.Num’
instance Real Int -- Defined in ‘GHC.Real’
instance Integral Int -- Defined in ‘GHC.Real’
instance Bounded Int -- Defined in ‘GHC.Enum’
Int
先述した通りIntは固定長整数です。
これを見る限り、java のLong.MAX_VALUEと同じなので 64bit ですね。
ghci> maxBound :: Int
9223372036854775807
例えばIntの上限値に+1すると、オーバーフローします。
ghci> ( maxBound :: Int ) + 1
-9223372036854775808
ところでmaxBoundはBoundedに定義されています。
他にBoundedのインスタンスになっているものは例えばBoolやOrderingがあります。
ghci> ( minBound, maxBound ) :: ( Bool, Bool )
(False,True)
ghci> ( minBound, maxBound ) :: ( Ordering, Ordering )
(LT,GT)
Integer
対してIntegerは多倍長整数です。気前よく巨大な整数を扱ってみましょう。
ghci> n = 9223372036854775807 :: Integer
ghci> n + 1
9223372036854775808
Intの上限に加算してもオーバーフローしてません。
もっと思い切りよく足しても全然大丈夫。
ghci> n + n
18446744073709551614
ところでIntegerがBoundedのインスタンスでないのは、多倍長整数なので上限がないからですね。ここまで理解していれば至極納得。
余談 型注釈
ところでサンプルコードで:: Intや:: Integerの様に型注釈をつけていますが、これをつけないとどうなるでしょうか。
ghci> n = 42
ghci> :t n
n :: Num p => p
まだ具体的には断定されていないみたいですね。
haskell は数値リテラルを必要になるまでは抽象的に扱っておいて、必要に応じて型を決めてくれます。
例えばこのnの定義後にtoInteger nなんてあれば haskell はIntegralだと思って扱おうとするわけです。
冒頭で触れた僕のわからなかったエラーの原因は完全にこれですね。
僕にはf 8 0 []って書いた時の値はIntに見えていたのですが、コンパイラはそう見てなかったということなのでしょう。悲しい 未熟ゆえのすれ違い。
ちょっと確認してみましょう、以下のコードはどちらも実行できます。
main = do
let n = 42
print $ toInteger n
-- print $ floor n
main = do
let n = 42
-- print $ toInteger n
print $ floor n
が、これは実行できません。
main = do
let n = 42
print $ toInteger n
print $ floor n
nはIntegralなのかRealFracなのかどっちだ、ってなってしまうからですね。
ですがこれは実行できます。
main = do
let n = 42
print $ toRational n
print $ floor n
これはRealFracの定義がこうなっているからです。
ghci> :info RealFrac
class (Real a, Fractional a) => RealFrac a where
絵を目で辿れば把握できそうですね。整理して良かった。
Int と Integer の変換
絵を見ると、NumにあるfromInteger :: Integer -> aを使ってNumにしてから:: Intで断定すればたどり着きそうです。
ghci> n = 5 :: Integer
ghci> :t fromInteger n
fromInteger n :: Num a => a
ghci> fromInteger n :: Int
5
で、想像の通り精度の低い方から高い方への変換はできますが、逆は正しくは行えません。
ghci> n = ( 9223372036854775807 :: Integer ) + 1
ghci> fromInteger n :: Int
-9223372036854775808
逆にIntからIntegerは絵にそのものずばりがあります。
ghci> n = 5 :: Int
ghci> toInteger n
5
余談 加算
絵を見ると、+はNumに定義されています。
実は普段の+はIntの足し算をしている気がするかもしれないけど、先ほどの余談で確認した通り明示しない限りIntとは断定されていません。
ghci> x = 1
ghci> y = 2
ghci> n = x + y
ghci> :t n
n :: Num a => a
ここからxとyがInt, Integer, Float, Doubleどれに断定されても大丈夫です。
ghci> x = 1 :: Int
ghci> y = 2 :: Int
ghci> n = x + y
ghci> :t n
n :: Int
ghci> x = 1 :: Float
ghci> y = 2 :: Float
ghci> n = x + y
ghci> :t n
n :: Float
ただし(+) :: a -> a -> aなので、xとyとnの型は全て同じである必要はあります。
ずれている場合は型を揃えてから計算します。
ghci> x = 1 :: Integer
ghci> y = 2 :: Int
ghci> n = x + ( toInteger y )
ghci> :t n
n :: Integer
ghci> n = ( fromInteger x ) + y
ghci> :t n
n :: Int
ex1 と ex2 の違いももう大丈夫です。ちゃんとわかります。
ex2 はせっかくfromIntegerでxをNumまで抽象化したけど、yがIntなのでxもIntに断定されている。なのでオーバーフローする。はず。
ghci> x = 9223372036854775807 :: Integer
ghci> y = 1 :: Int
ghci> x + ( toInteger y )
9223372036854775808
ghci> ( fromInteger x ) + y
-9223372036854775808
うん。ちゃんと理解できてる。
余談 除算
絵を見ると(+)はNumに定義されていますが(/)は違いますね。
なので普段行なっている4 / 2の演算は実はIntでもIntegerでも行われてないのです。
ghci> a = 4
ghci> b = 2
ghci> a / b
2.0
ghci> a = 4 :: Integer
ghci> b = 2 :: Integer
ghci> a / b
No instance for (Fractional Integer) arising from a use of '/'
Numに抽象化してから計算しましょう。
ghci> ( fromInteger a ) / ( fromInteger b )
2.0
Int と Integer の違いまとめ
-
Intは上限があるぞ -
Integerは上限が(メモリの許す限り)ないぞ -
IntからIntegerへの変換は値が壊れる可能性があるぞ - 型を明記しない限り、haskell は必要に応じて型を決めるぞ
ってことですね。
Float, Double
整数は押さえましたね。次は小数です。
Doubleの何が倍なんだって思ってましたが、勉強すれば明瞭ですね。
Floatは 32bit を使って、Doubleは 64bit を使って値を表現するということでした。だから倍精度。
コンピュータのメモリが有限である以上無限小数を完全に表現することは不可能なので、誤差が出る前提で扱わなければなりません。
例えば十進数の0.01は二進数だと有限で表現することができません。
有限で表現できない以上どこかで諦めなければいけず、それを繰り返せば誤差が大きくなるのはなんとなく感覚で理解できますね。
で、どんな誤差が出るか、です。試してみましょう。
ghci> f = 0.01 :: Float
ghci> sum $ replicate 100 f
0.99999934
ghci> d = 0.01 :: Double
ghci> sum $ replicate 100 d
1.0000000000000007
Doubleの方が1.0に近いですね。
相互変換
FloatとDoubleの変換も、IntとIntegerと同様に精度の高い方から低い方へ変換すると壊れます。
どうやって変換すれば良いのかな...
絵を見る限りではRationalを経由したら良いのかな...
ghci> f = 0.99999934 :: Float
ghci> d = 1.0000000000000007 :: Double
ghci> fromRational ( toRational f ) :: Double
0.9999993443489075
ghci> fromRational ( toRational d ) :: Float
1.0
絵には出せてなかったけど、調べたらこっちの方が良さそうかな。
ghci> realToFrac f :: Double
0.9999993443489075
ghci> realToFrac d :: Float
1.0
どちらにせよDoubleからFloatにした場合は欠けてしまっていますね。
またそもそも有限なので、単純に以下の様な値で誤差が出ます。
ghci> ( 10 :: Double ) / ( 3 :: Double )
3.3333333333333335
ghci> 1.00000001 :: Float
1.0
では誤差の出る小数の計算はどうすれば良いのでしょうか。
Rational
冒頭のベン図の様な絵で確認すると、有理数のことです。
さらっと冒頭で説明したこれのことですね。
実数は有理数と無理数に大別されますが、有理数は整数の比で表現できる数です。
haskell にはそのものずばりなRationalという型があって、そのまんま分数の様な形で扱っているみたいです。
ghci> 1 :: Rational
1 % 1
ghci> 0.01 :: Rational
1 % 100
RationalはRatio Integerのエイリアスになってるみたいです。
ghci> :info Rational
type Rational = GHC.Real.Ratio Integer -- Defined in ‘GHC.Real’
Ratioは単純に比という意味なので、Ratio Integerは ↓ を表現しているのかな、今ならわかる気がしますね。
分数は数の比で表現される数であり、一見有理数と同じな気がします。
が、有理数は整数の比なので、分数の方が広い概念です。
Rationalも普通に(+)が可能です。
ghci> r = 0.01 :: Rational
ghci> r
1 % 100
ghci> r + r
1 % 50
面白いですね、そのまんま分数の足し算みたいです。
これは 100 回加算しても誤差が出ない気がしますね。
ghci> r = 0.01 :: Rational
ghci> sum $ replicate 100 r
1 % 1
すごい。
小数にしたければ、こんな感じでしょうか。
ghci> fromRational ( sum $ replicate 100 r ) :: Float
1.0
もちろん、Rationalから小数にする時に誤差が出ることはありえます。
ghci> fromRational $ ( 10 :: Rational ) / ( 3 :: Rational )
3.3333333333333335
ここは気をつけなければいけませんね。
Real, RealFrac, Fractional, Floating, RealFloat
こいつらは一体何者なのでしょうか。
Real
Realはまぁシンプルに実数でしょう。
RealFrac
小数はdecimalで分数はfractionです。
有理数は整数の比で表現できる数です。
対してそれ以外の整数の比で表現できない数を無理数と言います。
これを思い出すと、RealFracは実数の分数なので**有理数も無理数も含むけど整数は含まない**と言ったところでしょうか...
整数を含むなら実数と変わらない気もするし、絵を見る限り整数は関係してません。
切り捨てや切り上げもここで定義されています。
Fractional
今の僕にとってはここは興味の対象外なので、かなり推測が入ってしまいます。お許しください。
Realとは関係してない分数なので、おそらくは虚数の分数を考慮しているのではないかと思います。
2/√-1とかですかね...
Floating, RealFloat
浮動小数点とは数値の表現方法の一つで、固定長の仮数部と指数部を持つ表現方法です。
これがそのもの floating point number だと思うのですが、Realを冠してないFloatingが何かは正直まだ理解できてません。
piとかはRealFloatだと思うんだけどな...
ちなみにこの記事まとめるまでは「FloatがRealFloatなのはわかるけどDoubleもRealFloatなのかよ。イミワカンネ。」
とか思ってたんですよね...
FloatとDoubleは仕組みは同じで精度の違いだけだからね...学んだよ...
余談 べき乗
実は冒頭で触れた僕のエラーの直接原因は(**)でした。
2 ** 3が8と出力されて欲しかったのに8.0と出力されてしまうので「よくわからんけど適当にそこかしこに:: Intって書いてみよ」とかやって変なことになったのです。
なぜ8.0になるのかは、もう学んだので大丈夫です。
Intで扱うと巨大な数でオーバーフローしますし、Integerにしたら小数が扱えないからですね。
浮動小数点にして先述のIEEE754の規格通り1.0e20みたいに大きい数を扱えば、オーバーフローしないし小数も大丈夫です。
ghci> 3000000000 ** 2
9.0e18
ghci> 4000000000 ** 2
1.6e19
ghci> 1.5 ** 2
2.25
仮に(**)の結果がIntだとすると、こんな感じになってしまうでしょう。
ghci> (***) a b = floor $ a ** b :: Int
ghci> 2 *** 3
8
ghci> 3000000000 *** 2
9000000000000000000
ghci> 4000000000 *** 2
-2446744073709551616
よく考えられてるんですねぇ。 不勉強でした、本当に恥ずかしい。
変換まとめ
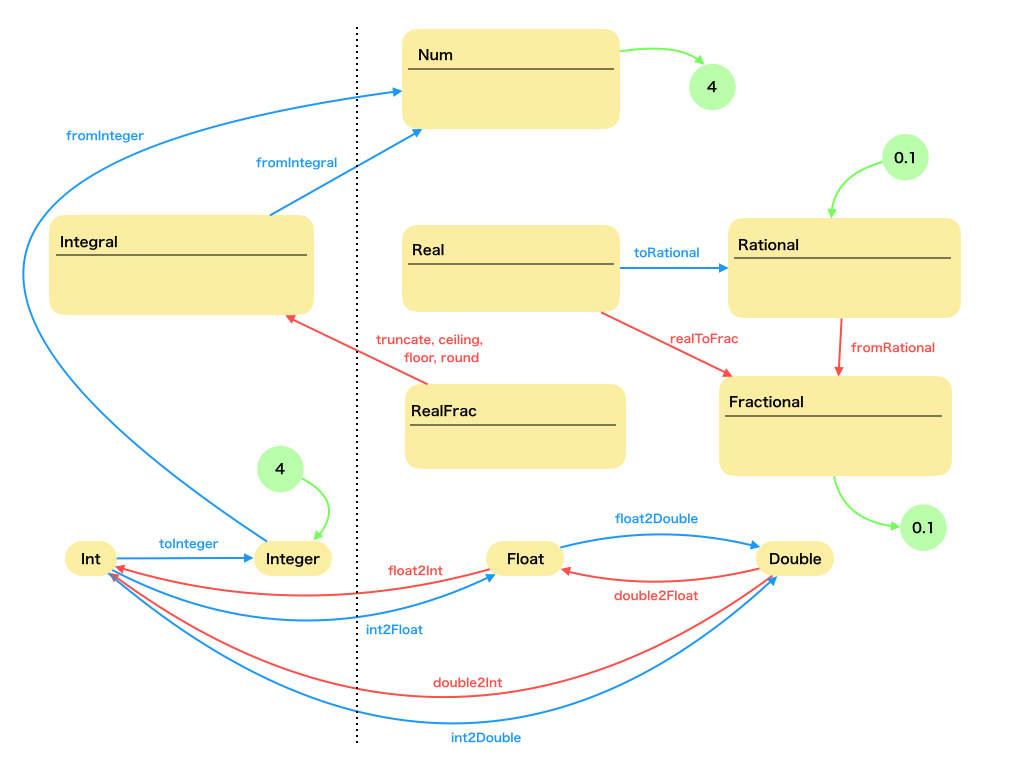
変換関数がたくさん出てきたので、絵を少し違う切り口で整理してみました。
青は安全な関数、赤は値が壊れる可能性がある関数です。
(int2FloatみたいなやつはGHC.Floatに定義してありました、要 import です。)
また、整数リテラルは最初にIntegerとして扱われてfromIntegerによってNumに、
小数リテラルは最初にRationalとして扱われてfromRationalによってFractionalに変換されるらしいです。
それぞれを緑で書き込んでみました。
整数になる点線を超える左向きの関数と、ベン図の外側に行く様な下向きの関数が危険なのがよくわかります。
まとめ
ながーい記事になったけど、やってみて感じた haskell における数値表現の要点は4つだけだ!
-
Intは扱える桁に限りがあるぜ -
Integerは動的にメモリを確保するので(メモリがある限り)上限はないぜ -
FloatとDoubleの違いは精度だけで、小数は有限のメモリでは表現できないので誤差が前提だぜ -
Rationalはすげーぜ、分数の形で値を扱うのでRational同士の計算においては誤差が出ないぜ
いやーそれにしても勉強になった。普段どれだけ適当にやってきたかを痛感した。
そしてこれを理解したらどうするかと言うと、やっぱドメインロジックとは切り離したいので value object を作って隠蔽するわけだ!
きっちり理解したので普段の業務(ドメイン実装)ではやっぱり使わないわけだ!なんというパラドクス!