こんにちはsurahotokeです。
今回は「Blender」でインボリュート平歯車の曲線を作成してみたので紹介します。
参考にしたサイトでは$(x, y)$で考えていましたが、歯車は点対象なので極形式$(r;\theta)$で作ってみました。
まず、関数描画の出来るアプリの「geogebra幾何」を使用し歯車を作ってから、BlenderのPythonで歯車を作成します。
歯幅$b$, モジュール$m$, 圧力角$\alpha$, 歯数$z$, 転移係数$x$を自由に設定できるものを作成します。(geogebra幾何では$z$, $x$は特殊な変数として扱われ、うまくいかないので代わりに$z_1$, $x_1$を使用します)
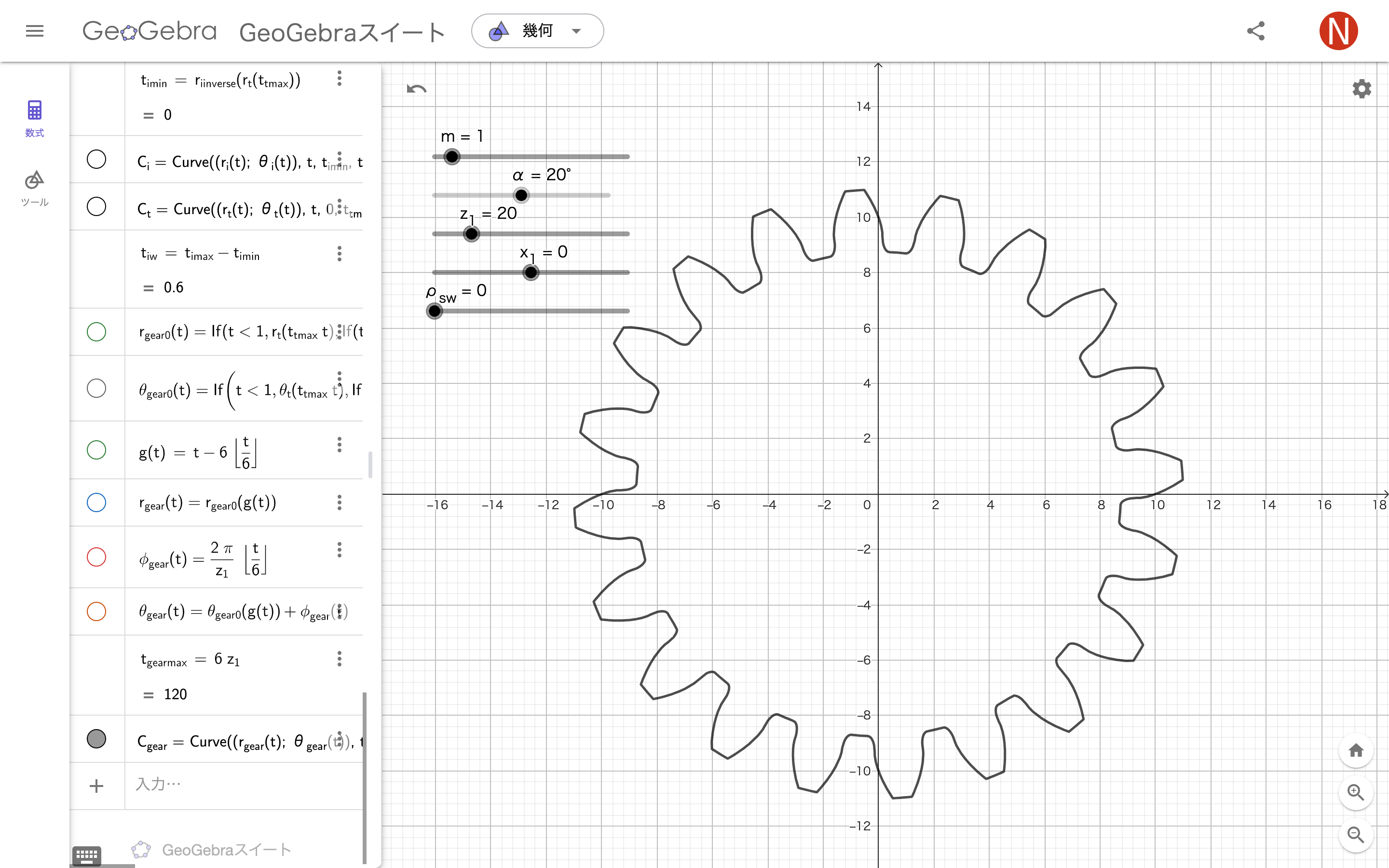
今回作成したもの
geogebra:https://www.geogebra.org/m/xbrh2wnu
github:https://github.com/surahotoke/create-involute-gear-in-Blender
目次:
各用語の解説
| 項目 | 記号 | 関係 | 単位 | 軽い説明 |
|---|---|---|---|---|
| 歯幅 | $b$ | 任意 | mm | 歯車の分厚さ |
| モジュール | $m$ | 任意 | mm | 歯車のサイズを表し、この値と圧力角が一致していれば歯車同士が噛み合う |
| 圧力角 | $\alpha$ | 任意 | $°, rad$ | 歯の形を表し、JISでは20°と定められている |
| 歯数 | $z$ | 任意 | - | 歯車の歯の数 |
| 転移係数 | $x$ | 任意 | - | 歯を内側や外側にずらす係数 |
| 切り下げ限界転移係数 | $x_c$ | $1-\frac z2\sin^2(\alpha)$ | - | 転移係数がこの値を下回ると切り下げが発生する(本当は丸みを考慮するとこれよりもう少しだけ小さい) |
| ラック歯先の丸み | $\rho$ | $0(m\leq0.4)$$0.38m(1\lt m)$$0or0.38m(else)$ | mm | JIS B 4350によるとこんな値です |
| 基準円直径 | $d$ | $zm$ | mm | 歯車の基準となる円の直径 |
| 基準円半径 | $r$ | $\frac d2$ | mm | …(省略)…半径 |
| 基礎円直径 | $d_b$ | $d\cos(\alpha)$ | mm | 基準円直径に圧力角を考慮した円の直径。トロコイド部分を考慮しない場合、基礎円からインボリュート曲線を生やす |
| 基礎円半径 | $r_b$ | $\frac{d_b}2$ | mm | …(省略)…半径 |
| 歯末のたけ | $h_a$ | $(1+x)m$ | mm | 歯の先端から基準円までの距離 |
| 歯先円直径 | $d_a$ | $d+2h_a$ | mm | 歯の先端の円の直径 |
| 歯先円半径 | $r_a$ | $\frac{d_a}2$ | mm | …(省略)…半径 |
| 歯元のたけ | $h_f$ | $(1.25-x)m$ | mm | 歯の根元から基準円までの距離 |
| 歯底円直径 | $d_f$ | $d-2h_f$ | mm | 歯の根元の円の直径 |
| 歯底円半径 | $r_f$ | $\frac{d_f}2$ | mm | …(省略)…半径 |
| 丸みまでのたけ | $h_r$ | $h_f-\rho$ | mm | ラック歯先の丸みの円の中心から歯底円までの距離 |
| $---$ | $---$ | $---$ | $---$ | $---$ |
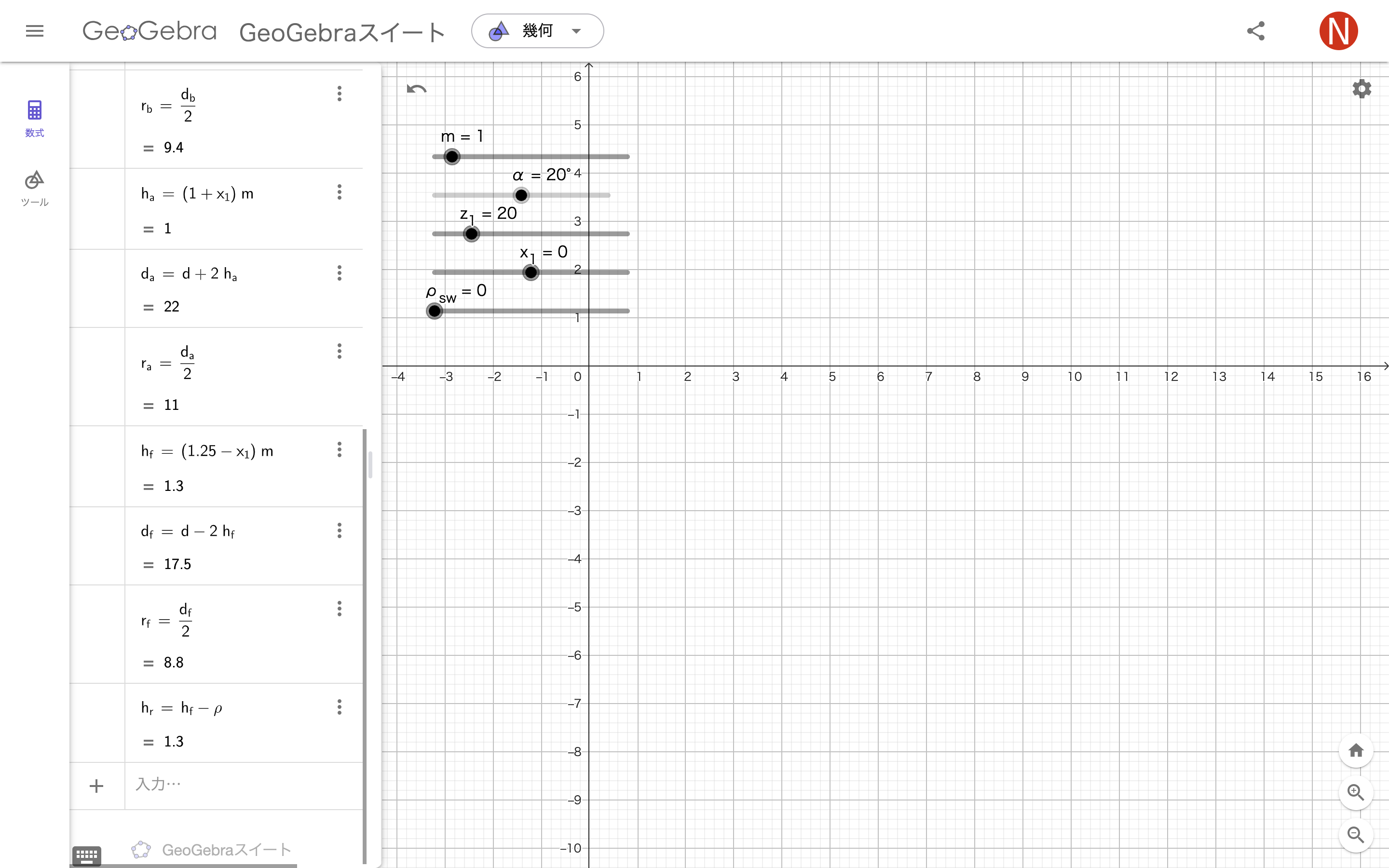
# 設定から軸やメモリの表示を変えられる
m=Slider(0.1,10)
α=Slider(0,40°)
# αを20°にしておく
z_{1}=Slider(1,100,1)
# z_{1}をいくらか上げておく
x_{1}=Slider(-2,2)
ρ_{sw}=Slider(0,1,1)
ρ=If(m≤0.4,0,If(1<m,0.38 m,0.38 m ρ_{sw}))
d=z_{1} m
r=((d)/(2))
d_{b}=d cos(α)
r_{b}=((d_{b})/(2))
h_{a}=(1+x_{1}) m
d_{a}=d+2 h_{a}
r_{a}=((d_{a})/(2))
h_{f}=(1.25-x_{1}) m
d_{f}=d-2 h_{f}
r_{f}=((d_{f})/(2))
h_{r}=h_{f}-ρ
各曲線の数式
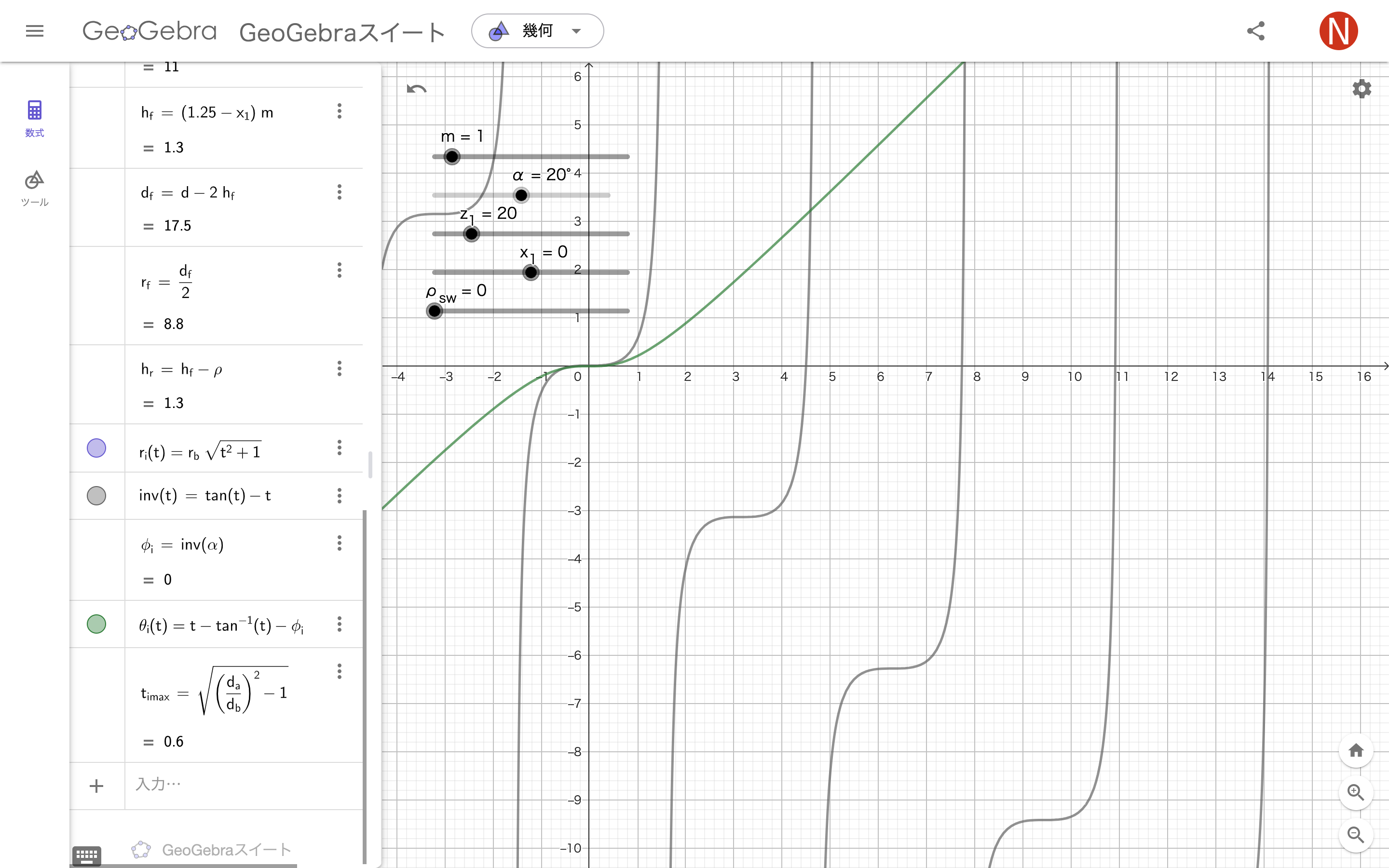
インボリュート部分
半径$r_i(t)=r_b\sqrt{t^2+1}$
インボリュート関数$inv(t)=\tan(t)-t$
ずれ$\phi_i=inv(\alpha)$
角度$\theta_i(t)=t-\arctan(t)-\phi_i$
tの最小値$t_{imin}=(後で求める)$
$r_i(t)=r_aを解き、$
tの最大値$t_{imax}=\sqrt{\left(\frac{d_a}{d_b}\right)^2-1}$
曲線$C_i(t)=Curve\Bigl(\bigl(r_i(t);\theta_i(t)\bigr),t,t_{imin},t_{imax}\Bigr)$
r_{i}(t)=r_{b} sqrt(t^(2)+1)
inv(t)=tan(t)-t
ϕ_{i}=inv(α)
θ_{i}(t)=t-tan^(-1)(t)-ϕ_{i}
t_{imax}=sqrt((((d_{a})/(d_{b})))^(2)-1)
歯先円部分
半径$r_a$
ずれ$\phi_a=\theta_i(t_{imax})$
角度$\theta_a(t)=t+\phi_a$
tの最小値$t_{amin}=0$
tの最大値$t_{amax}=\frac\pi z-2\phi_a$
曲線$C_a(t)=Curve\Bigl(\bigl(r_a;\theta_a(t)\bigr),t,0,t_{amax}\Bigr)$
ϕ_{a}=θ_{i}(t_{imax})
θ_{a}(t)=t+ϕ_{a}
t_{amax}=((π)/(z_{1}))-2 ϕ_{a}
C_{a}=Curve((r_{a}; θ_{a}(t)),t,0,t_{amax})
前の部分は隠した。(関数やスライダーなどの式の⚫︎の部分を押すと◯になり隠せる)
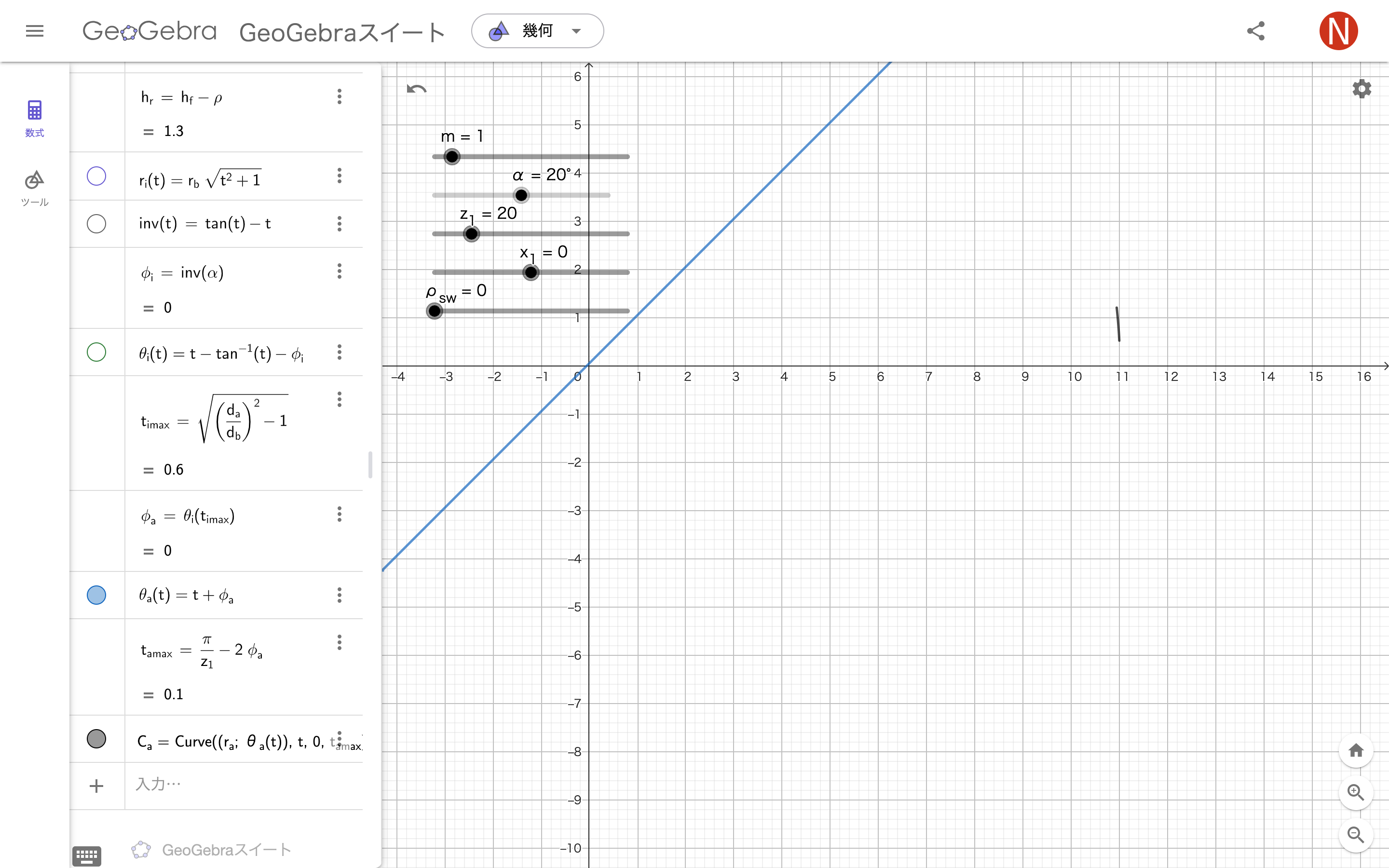
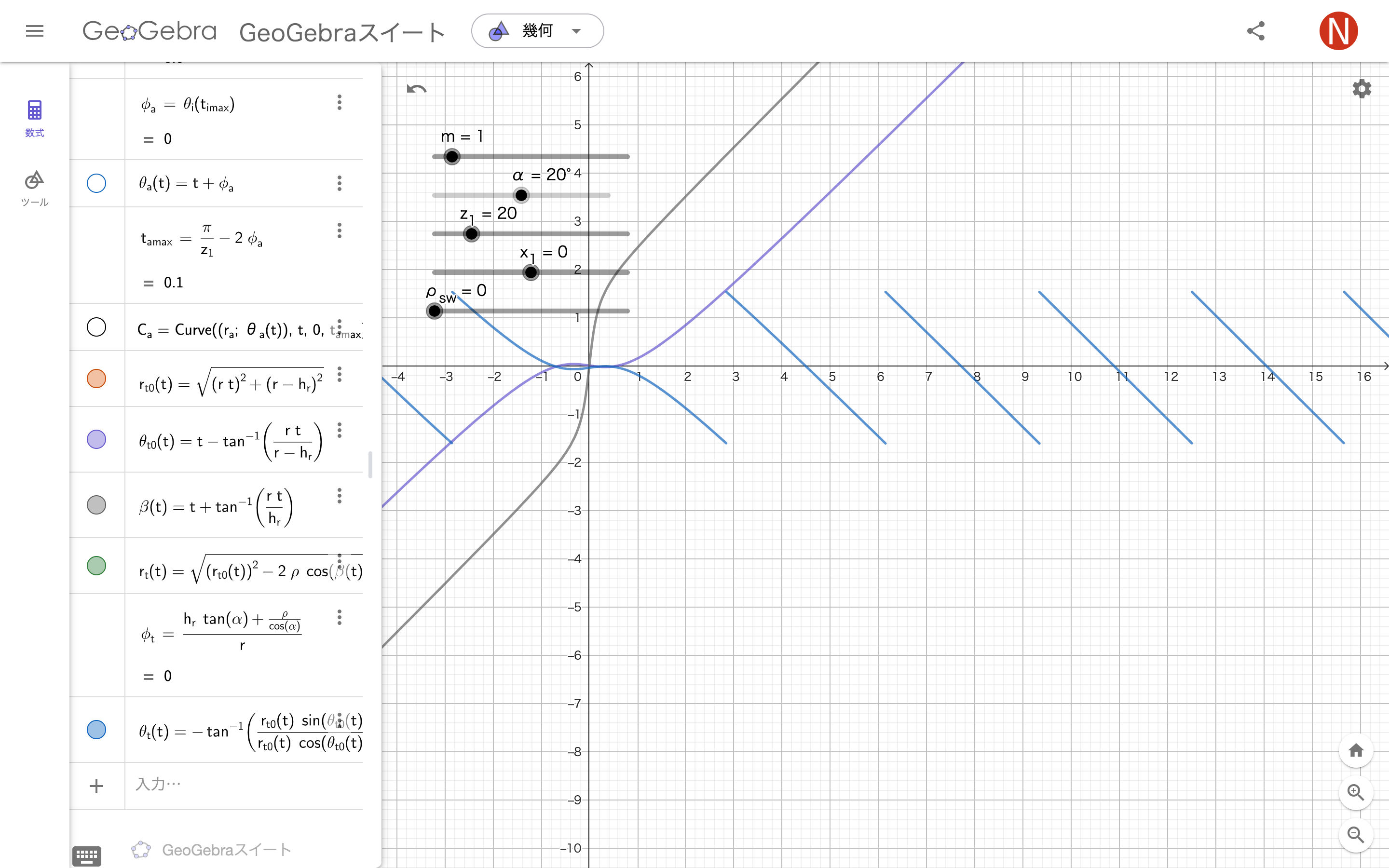
トロコイド部分
$r_{t0}(t)=\sqrt{(rt)^2+(r-h_r)^2}$
$\theta_{t0}(t)=t-\arctan\left(\frac{rt}{r-h_r}\right)$
$\beta(t)=t+\arctan\left(\frac{rt}{h_r}\right)$
半径$r_t(t)=\sqrt{r_{t0}(t)^2-2\rho\cos\bigl(\beta(t)-\theta_{t0}(t)\bigr)r_{t0}(t)+\rho^2}$
ずれ$\phi_t=\frac{h_r\tan(\alpha)+\frac\rho{\cos(\alpha)}}r$
角度$\theta_t(t)=-\arctan\left(\frac{r_{t0}(t)\sin\bigl(\theta_{t0}(t)\bigr)-\rho\sin\bigl(\beta(t)\bigr)}{r_{t0}(t)\cos\bigl(\theta_{t0}(t)\bigr)-\rho\cos\bigl(\beta(t)\bigr)}\right)-\phi_t$
tの最小値$t_{tmin}=0$
tの最大値$t_{tmax}=(後で求める)$
曲線$C_t(t)=Curve\Bigl(\bigl(r_t(t);\theta_t(t)\bigr),t,0,t_{tmax}\Bigr)$
r_{t0}(t)=sqrt((r t)^(2)+(r-h_{r})^(2))
θ_{t0}(t)=t-tan^(-1)(((r t)/(r-h_{r})))
β(t)=t+tan^(-1)(((r t)/(h_{r})))
r_{t}(t)=sqrt((r_{t0}(t))^(2)-2 ρ cos(β(t)-θ_{t0}(t)) r_{t0}(t)+ρ^(2))
ϕ_{t}=((h_{r} tan(α)+((ρ)/(cos(α))))/(r))
θ_{t}(t)=-tan^(-1)(((r_{t0}(t) sin(θ_{t0}(t))-ρ sin(β(t)))/(r_{t0}(t) cos(θ_{t0}(t))-ρ cos(β(t)))))-ϕ_{t}
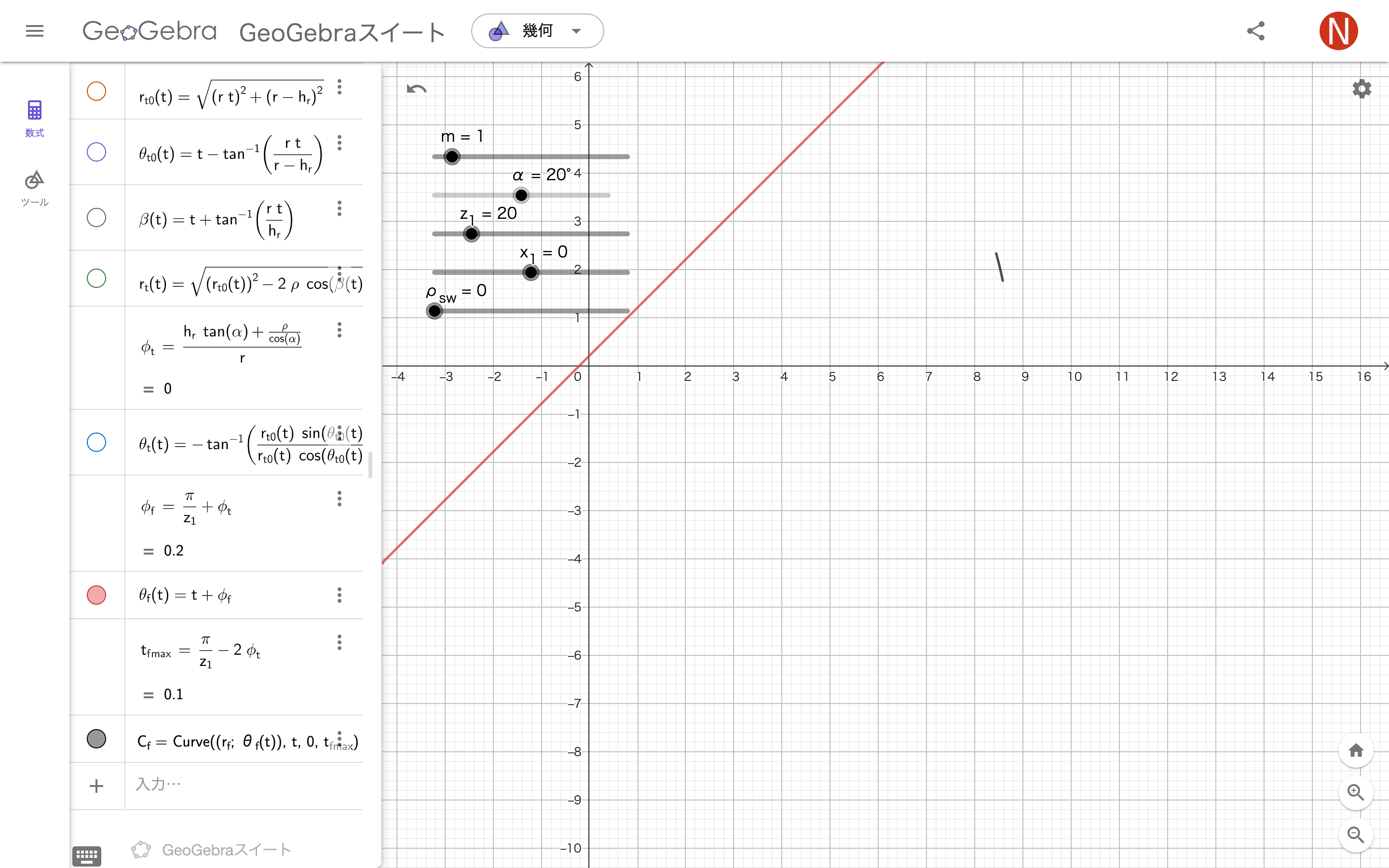
歯底円部分
半径$r_f$
ずれ$\phi_f=\frac\pi z+\phi_t$
角度$\theta_f(t)=t+\phi_f$
tの最小値$t_{fmin}=0$
tの最大値$t_{fmax}=\frac\pi z-2\phi_t$
曲線$C_f(t)=Curve\Bigl(\bigl(r_f;\theta_f(t)\bigr),t,0,t_{fmax}\Bigr)$
ϕ_{f}=((π)/(z_{1}))+ϕ_{t}
θ_{f}(t)=t+ϕ_{f}
t_{fmax}=((π)/(z_{1}))-2 ϕ_{t}
C_{f}=Curve((r_{f}; θ_{f}(t)),t,0,t_{fmax})
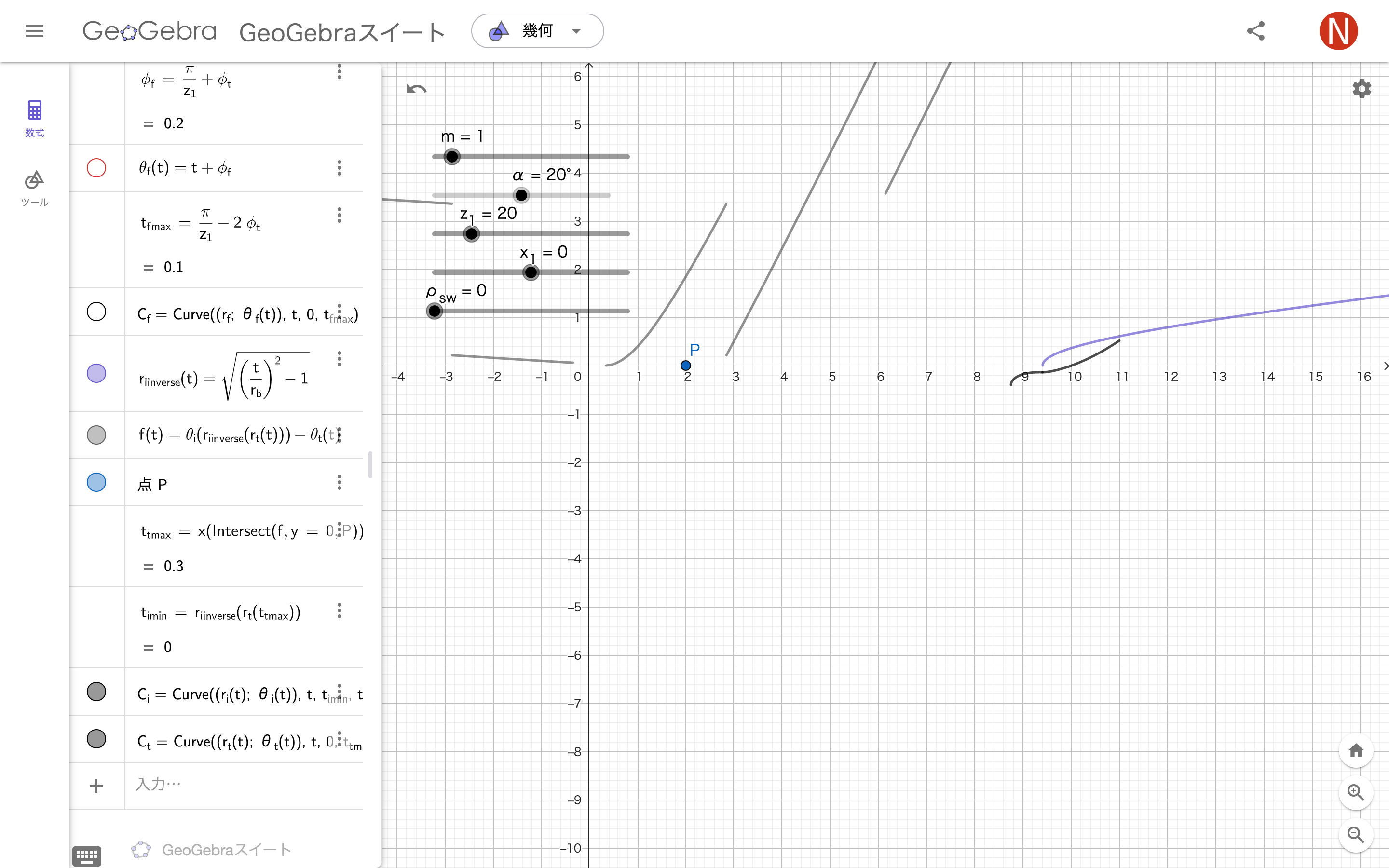
インボリュート-トロコイド交点を求める
曲線$C_i(t)=Curve\Bigl(\bigl(r_i(t);\theta_i(t)\bigr),t,t_{imin},t_{imax}\Bigr)$
曲線$C_t(t)=Curve\Bigl(\bigl(r_t(t);\theta_t(t)\bigr),t,0,t_{tmax}\Bigr)$
正確には交点を求めるのではなく、交点でのt(つまり$t_{imin}$と$t_{tmax}$)を求めます。
求め方
方程式$C_i(t_{imin})=C_t(t_{tmax})$を解けば良いです。
よって、
\begin{cases}
r_i(t_{imin})=r_t(t_{tmax})\\
\theta_i(t_{imin})=\theta_t(t_{tmax})
\end{cases}
$r_i(t)$と$\theta_i(t)$の逆関数を用いると、
$t_{imin}=r_i^{-1}\bigl(r_t(t_{tmax})\bigr)=\theta_i^{-1}\bigl(\theta_t(t_{tmax})\bigr)$
が得られる。ここで、$r_i(t)$の逆関数は計算でき、
$r_i^{-1}(t)=\sqrt{\left(\frac t{r_b}\right)^2-1}$
となる。よって、
$\theta_i\Bigl(r_i^{-1}\bigl(r_t(t_{tmax})\bigr)\Bigr)=\theta_t(t_{tmax})$
のように変形すると$t_{tmax}$のみの等式が得られ、
$f(t)=\theta_i\Bigl(r_i^{-1}\bigl(r_t(t)\bigr)\Bigr)-\theta_t(t)$
とすると、関数f(t)とt軸との交点を求めれば良くなり、t軸との交点はgeogebraでは簡単に出せるので、$t_{tmax}$が求まる。
更に、$t_{imin}=r_i^{-1}\bigl(r_t(t_{tmax})\bigr)$より、$t_{imin}$も求まる。
r_{iinverse}(t)=sqrt((((t)/(r_{b})))^(2)-1)
f(t)=θ_{i}(r_{iinverse}(r_{t}(t)))-θ_{t}(t)
P=(2,0)
t_{tmax}=x(Intersect(f,y=0,P))
# 点P付近のfとy=0との交点のx座標ということ
t_{imin}=r_{iinverse}(r_{t}(t_{tmax}))
C_{i}=Curve((r_{i}(t); θ_{i}(t)),t,t_{imin},t_{imax})
C_{t}=Curve((r_{t}(t); θ_{t}(t)),t,0,t_{tmax})
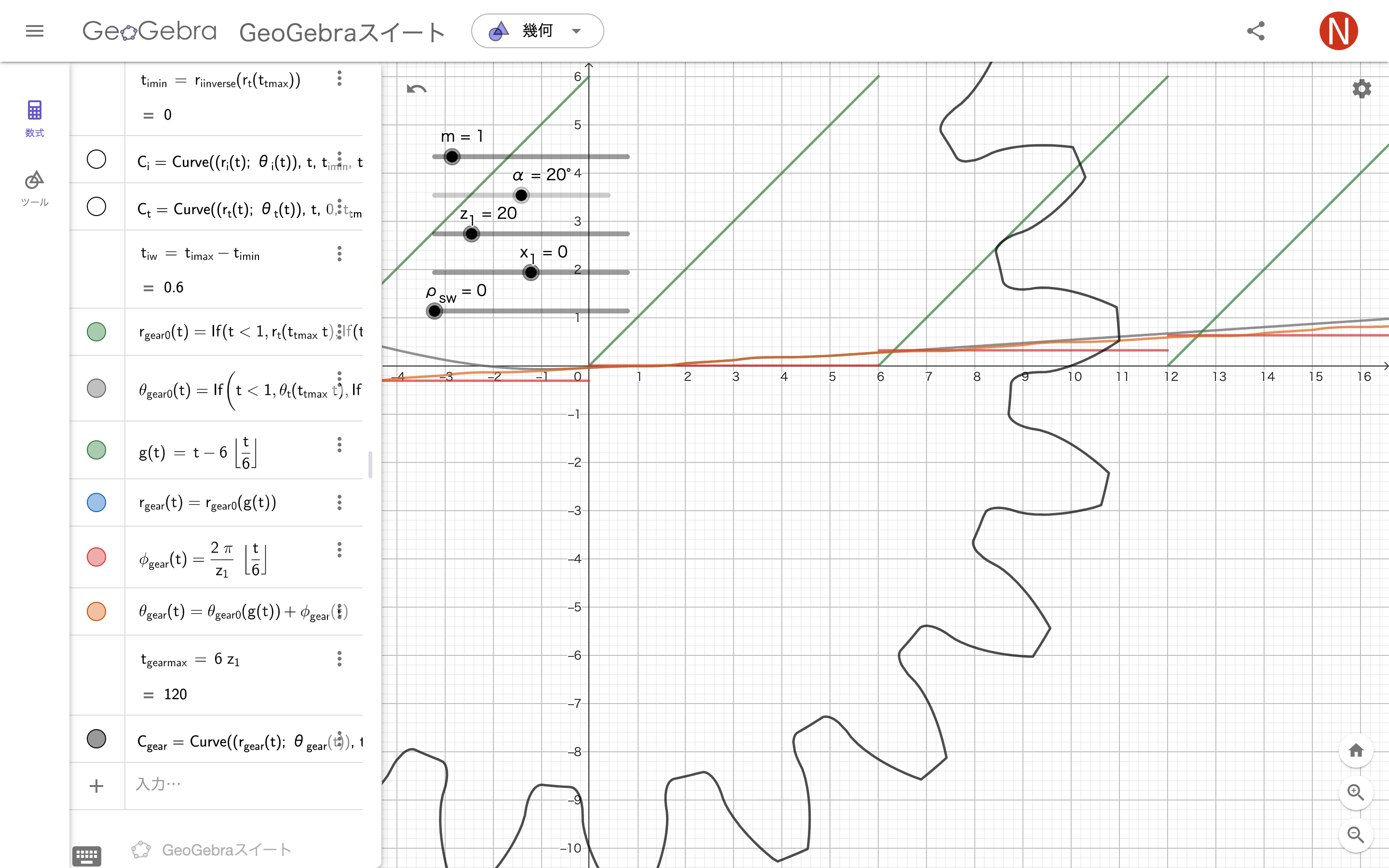
1つの曲線にまとめる
$t_{iw}=t_{imax}-t_{imin}$
として、
r_{gear0}(t)=\left\{
\begin{array}{ll}
r_t(t_{tmax}t) & (t \lt 1)\\
r_i\bigl(t_{imin}+t_{iw}(t-1)\bigr) & (t \lt 2)\\
r_a & (t \lt 3)\\
r_i\bigl(t_{imax}-t_{iw}(t-3)\bigr) & (t \lt 4)\\
r_t\bigl(t_{tmax}(5-t)\bigr) & (t \lt 5)\\
r_f & (else)
\end{array}
\right.
\theta_{gear0}(t)=\left\{
\begin{array}{ll}
\theta_t(t_{tmax}t) & (t \lt 1)\\
\theta_i\bigl(t_{imin}+t_{iw}(t-1)\bigr) & (t \lt 2)\\
\theta_a\bigl(t_{amax}(t-2)\bigr) & (t \lt 3)\\
\frac\pi z-\theta_i\bigl(t_{imax}-t_{iw}(t-3)\bigr) & (t \lt 4)\\
\frac\pi z-\theta_t\bigl(t_{tmax}(5-t)\bigr) & (t \lt 5)\\
\theta_f\bigl(t_{fmax}(t-5)\bigr) & (else)
\end{array}
\right.
$g(t)=t-6\lfloor\frac t6\rfloor$
半径$r_{gear}(t)=r_{gear0}\bigl(g(t)\bigr)$
ずれ$\phi_{gear}(t)=\frac{2\pi}z\lfloor\frac t6\rfloor$
角度$\theta_{gear}(t)=\theta_{gear0}\bigl(g(t)\bigr)+\phi_{gear}(t)$
tの最小値$t_{gearmin}=0$
tの最大値$t_{gearmax}=6z$
曲線$C_{gear}(t)=Curve\Bigl(\bigl(r_{gear}(t);\theta_{gear}(t)\bigr),t,0,t_{gearmax}\Bigr)$
t_{iw}=t_{imax}-t_{imin}
r_{gear0}(t)=If(t<1, r_{t}(t_{tmax} t), If(t<2, r_{i}(t_{imin}+t_{iw} (t-1)), If(t<3, r_{a}, If(t<4, r_{i}(t_{imax}-t_{iw} (t-3)), If(t<5, r_{t}(t_{tmax} (5-t)), r_{f})))))
θ_{gear0}(t)=If(t<1, θ_{t}(t_{tmax} t), If(t<2, θ_{i}(t_{imin}+t_{iw} (t-1)), If(t<3, θ_{a}(t_{amax} (t-2)), If(t<4, ((π)/(z_{1}))-θ_{i}(t_{imax}-t_{iw} (t-3)), If(t<5, ((π)/(z_{1}))-θ_{t}(t_{tmax} (5-t)), θ_{f}(t_{fmax} (t-5)))))))
g(t)=t-6 floor(((t)/(6)))
r_{gear}(t)=r_{gear0}(g(t))
ϕ_{gear}(t)=((2 π)/(z_{1})) floor(((t)/(6)))
θ_{gear}(t)=θ_{gear0}(g(t))+ϕ_{gear}(t)
t_{gearmax}=6 z_{1}
C_{gear}=Curve((r_{gear}(t); θ_{gear}(t)),t,0,t_{gearmax})
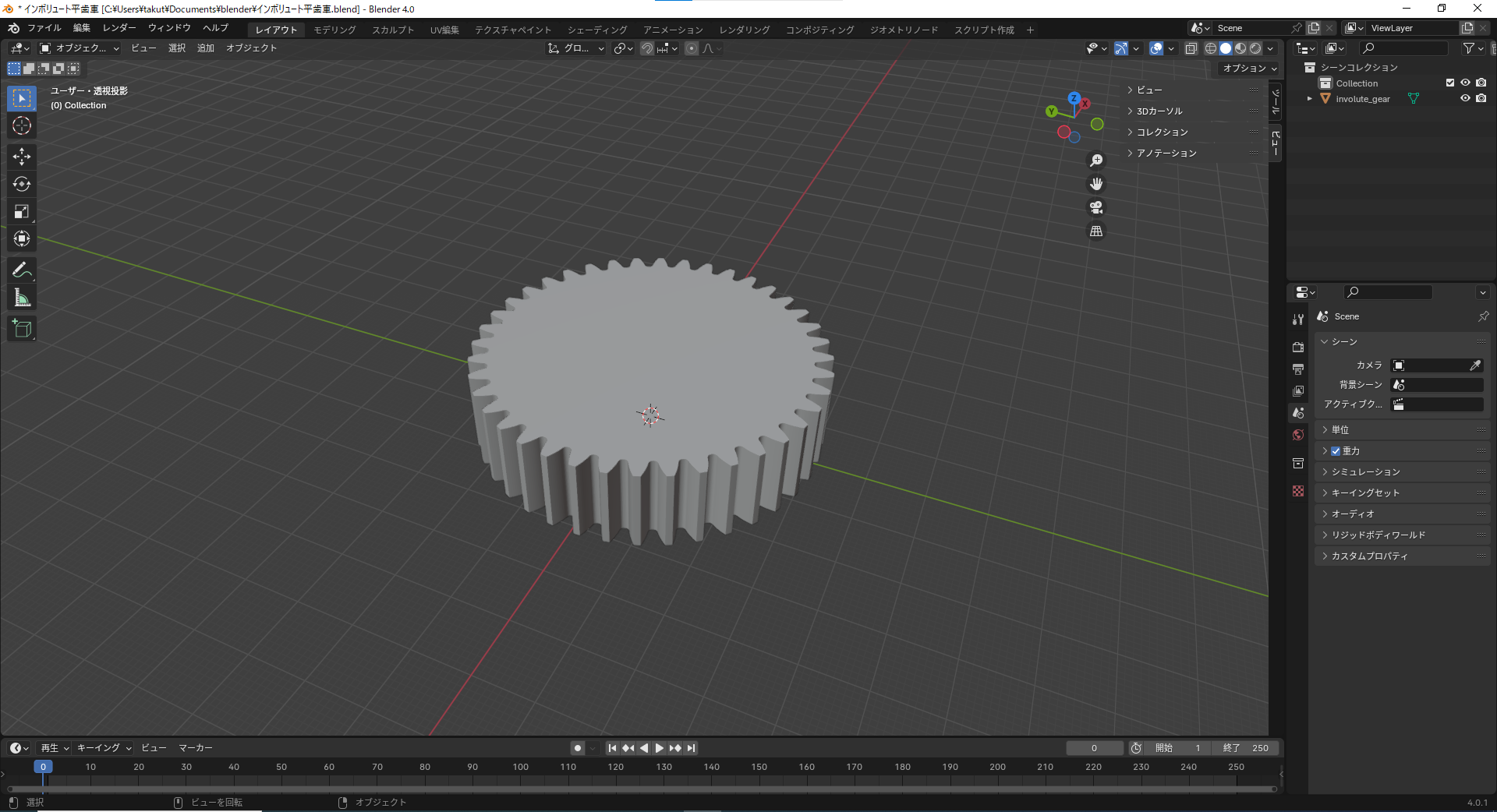
Blenderで歯車オブジェクトを作成する
pythonファイルの作り方・実行
まずBlenderを開きます。そして画面の右上にあるスクリプト作成という部分をクリックします。
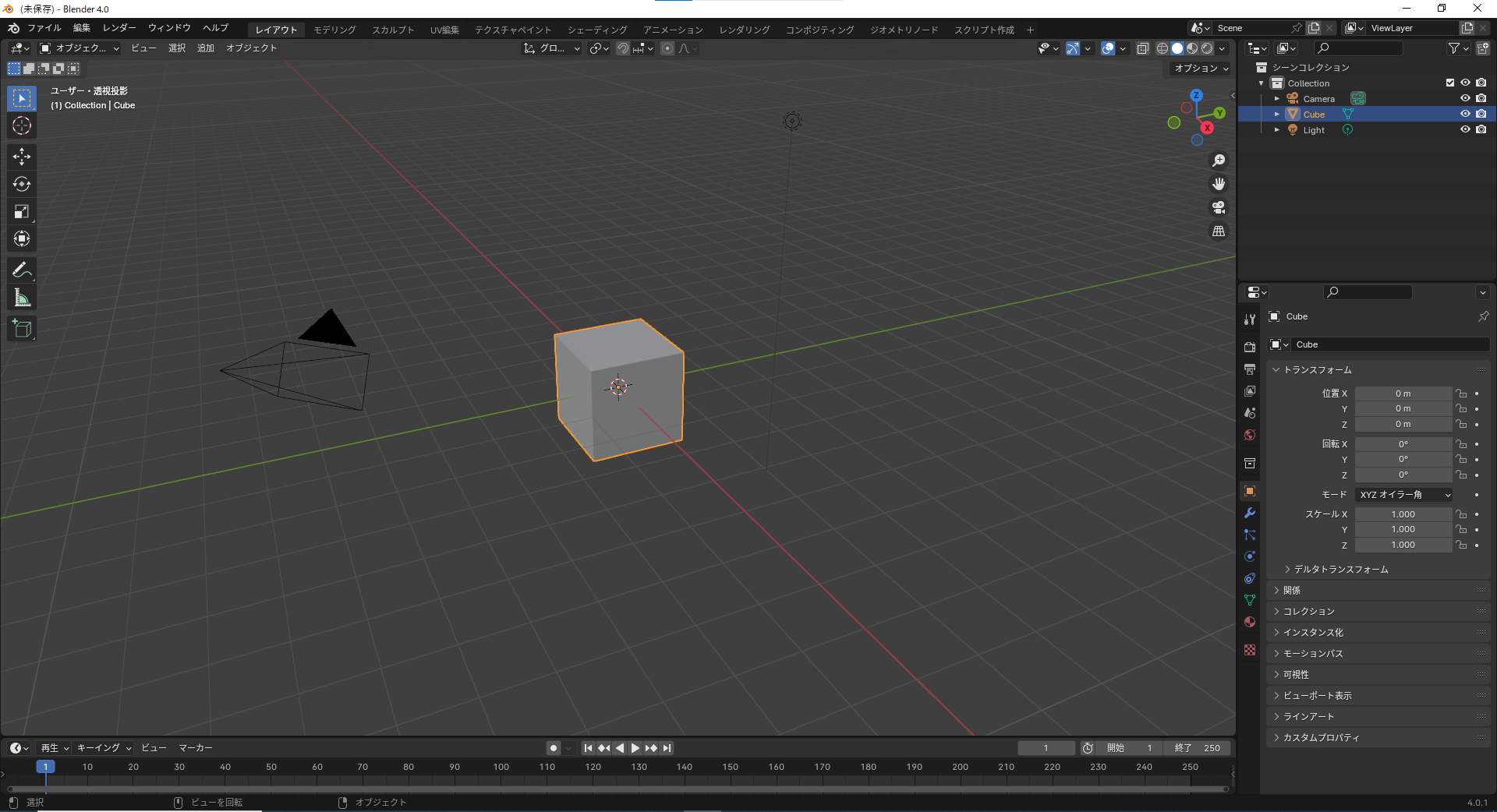
すると以下のようになります。
次に画面の上の中央にある+新規という部分をクリックします。
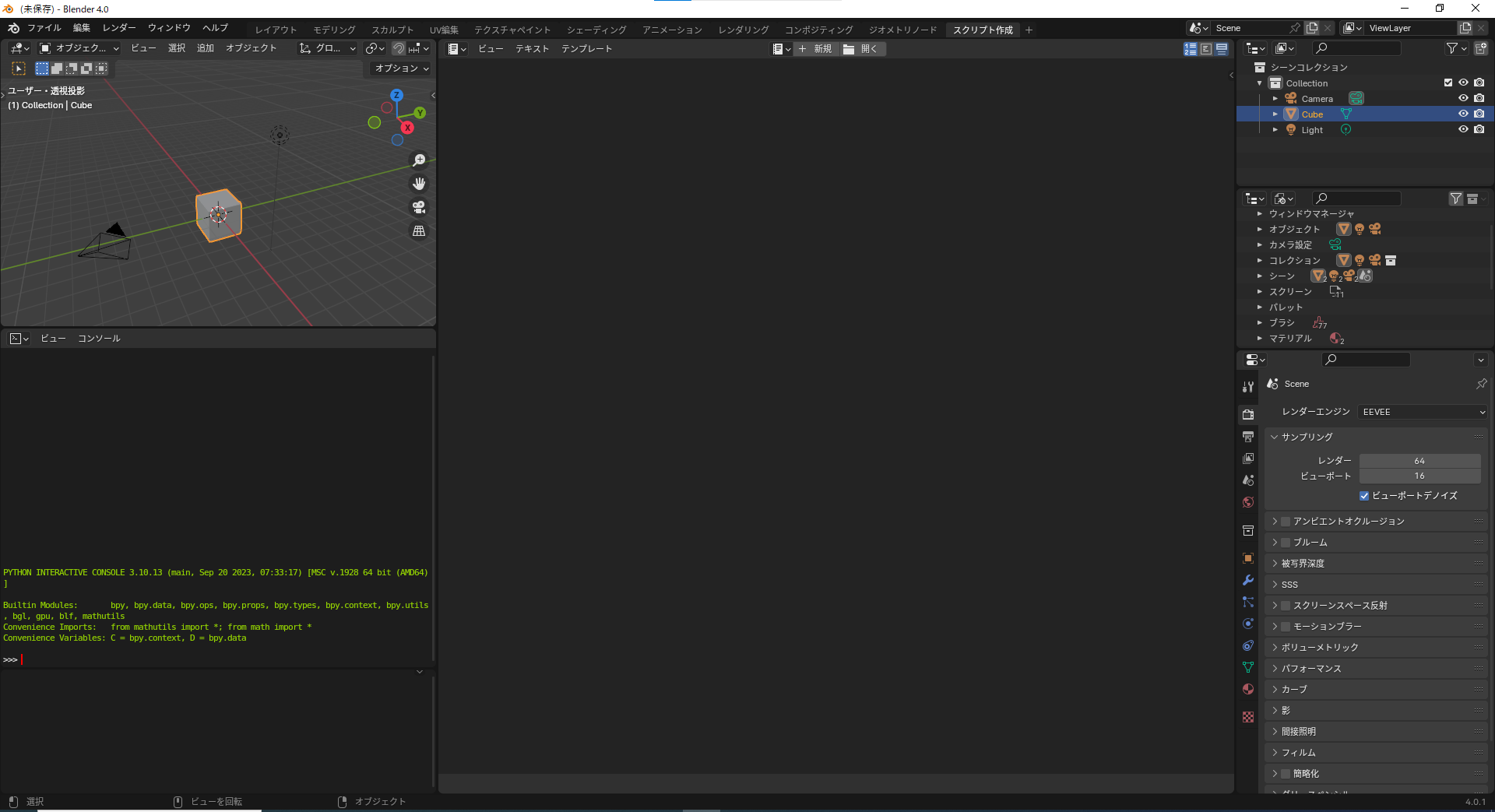
すると以下のようになります。
同じあたりにあるテキストと書かれた部分にpythonファイルの名前を入力します。(例:gear.py)
その下のエリアがコードの部分で、右にある▷が実行ボタンです。
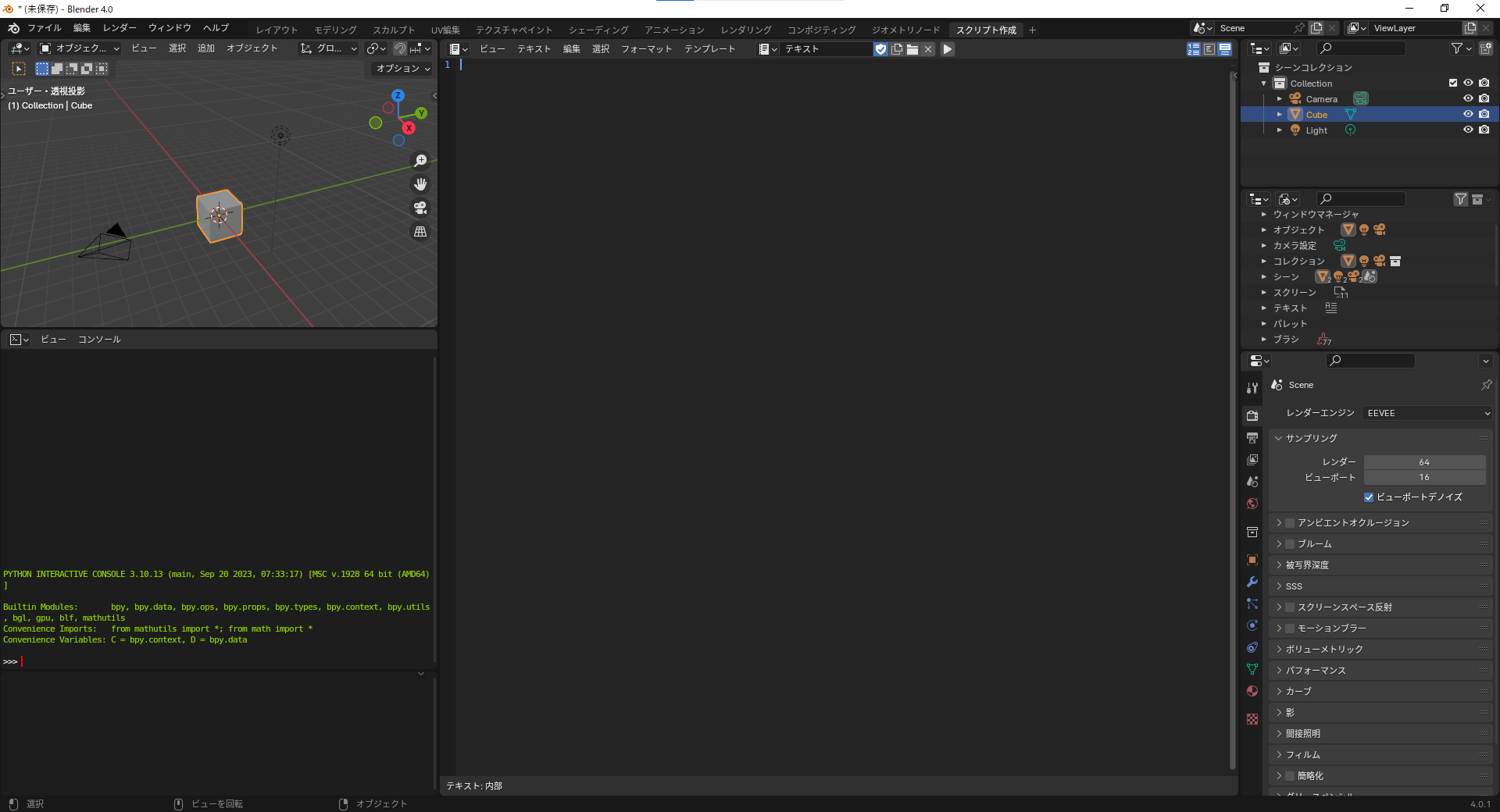
上のやや左側にあるレイアウトという部分をクリックすると元の画面に戻ります。
pythonでのインボリュート-トロコイド交点の求め方(ニュートン法)
ニュートン法を使用し、求めます。
初期値
geogebraでモジュール$m$, 圧力角$\alpha$, 歯数$z$, 転移係数$x$を色々な値に動かし、関数f(t)の動きを観察すると分かるのですがx軸との交点は大体tが1より小さいところにあります。また、tが小さい部分では値が出ず、大きい部分では正の方向に値が増えています。よってニュートン法の初期値を2に設定します。
geogebraで値を変える時に複雑な関数を表示しているととても重くなるので、関数を非表示にしておきましょう。
計算回数
64回の反復計算を行います。正直こんなにやる必要は無いですが、1回しか求めないので、別に重くなるわけじゃない為、とりあえず64回にしときました。
組み合わせる
今までに出してきた式を組み合わせます。
import math
import bpy
def clear():
for item in bpy.data.meshes:
bpy.data.meshes.remove(item)
def create(name="involute_gear", m=1, b=10, alpha_deg=20, z=40, x=0, t_len = 10, x_csw=False, rho_sw=False):
def r_i(t):
return r_b * math.sqrt(t**2 + 1)
def inv(t):
return math.tan(t) - t
def theta_i(t):
return t - math.atan(t) - phi_i
def theta_a(t):
return t + phi_a
def r_t0(t):
return math.sqrt((r * t)**2 + (r - h_r)**2)
def theta_t0(t):
return t - math.atan(r * t / (r - h_r))
def beta(t):
return t + math.atan(r * t / h_r)
def r_t(t):
return math.sqrt(r_t0(t)**2 - 2 * rho * math.cos(beta(t) - theta_t0(t)) * r_t0(t) + rho**2)
def theta_t(t):
return -math.atan((r_t0(t) * math.sin(theta_t0(t)) - rho * math.sin(beta(t))) / (r_t0(t) * math.cos(theta_t0(t)) - rho * math.cos(beta(t)))) - phi_t
def theta_f(t):
return t + phi_f
def r_iinverse(t):
return math.sqrt((t / r_b)**2 - 1)
def f(t):
return theta_i(r_iinverse(r_t(t))) - theta_t(t)
def find_an_approximate_f_inverse(t):
# 初期値
t_approx = 2
# ニュートン法による反復
for _ in range(64):
# f(t_approx)とその導関数の計算
f_t_approx = f(t_approx)
f_prime_t_approx = (f(t_approx + 1e-6) - f_t_approx) / 1e-6
# ニュートン法の反復式
t_approx -= f_t_approx / f_prime_t_approx
return t_approx
def r_gear0(t):
if t < 1:
return r_t(t_tmax * t)
elif t < 2:
return r_i(t_imin + t_iw * (t - 1))
elif t < 3:
return r_a
elif t < 4:
return r_i(t_imax - t_iw * (t - 3))
elif t < 5:
return r_t(t_tmax * (5 - t))
else:
return r_f
def theta_gear0(t):
if t < 1:
return theta_t(t_tmax * t)
elif t < 2:
return theta_i(t_imin + t_iw * (t - 1))
elif t < 3:
return theta_a(t_amax * (t - 2))
elif t < 4:
return math.pi/z - theta_i(t_imax - t_iw * (t - 3))
elif t < 5:
return math.pi/z - theta_t(t_tmax * (5 - t))
else:
return theta_f(t_fmax * (t - 5))
def g(t):
return t - 6 * math.floor(t / 6)
def r_gear(t):
return r_gear0(g(t))
def phi_gear(t):
return 2 * math.pi * math.floor(t / 6) / z
def theta_gear(t):
return theta_gear0(g(t)) + phi_gear(t)
def C_gear(t, b):
x = r_gear(t) * math.cos(theta_gear(t))
y = r_gear(t) * math.sin(theta_gear(t))
z = b
return [x, y, z]
def linspace(start, stop, num=50):
if num <= 1:
return [start]
step = (stop - start) / (num - 1)
return [start + step * i for i in range(num)]
# degreeをradに変換
alpha = math.radians(alpha_deg)
# x
x_c = 1 - z * math.sin(alpha)**2 / 2
if x_csw:
x = x_c
# rho
rho = 0
if rho_sw:
rho = 0.38 * m
if m <= 0.4:
rho = 0
elif 1 < m:
rho = 0.38 * m
# normal
d = z * m
r = d/2
d_b = d * math.cos(alpha)
r_b = d_b/2
h_a = (1 + x) * m
d_a = d + 2 * h_a
r_a = d_a/2
h_f = (1.25 - x) * m
d_f = d - 2 * h_f
r_f = d_f/2
h_r = h_f - rho
# C_i
phi_i = inv(alpha)
t_imax = math.sqrt((d_a/d_b)**2 - 1)
# C_a
phi_a = theta_i(t_imax)
t_amax = math.pi/z - 2 * phi_a
# C_t
phi_t = (h_r * math.tan(alpha) + rho/math.cos(alpha))/r
# C_f
phi_f = math.pi/z + phi_t
t_fmax = math.pi/z - 2 * phi_t
# t_tmax, t_imin
t_tmax = find_an_approximate_f_inverse(0)
t_imin = r_iinverse(r_t(t_tmax))
# simply
t_iw = t_imax - t_imin
# 分割数
t_len *= 6 * z
# tの範囲
t_max = 6 * z
lattice_t = linspace(0, t_max, t_len+1)[:-1]
if b == 0:
# 点を追加
verts = [C_gear(t, 0) for t in lattice_t]
# 面
faces = [[t for t in range(len(lattice_t))]]
else:
# 点を追加
verts = [C_gear(t, b) for b in [0, b] for t in lattice_t]
# 上下面
faces = [[t+b for t in range(len(lattice_t))] for b in [0, t_len]]
# 側面を追加
side_faces = []
for i in range(t_len):
side_faces.extend([[i, (i + 1)%t_len, (i + 1)%t_len + t_len, i + t_len]])
faces += side_faces
# 作成
msh = bpy.data.meshes.new(name + "_mesh") #Meshデータの宣言
msh.from_pydata(verts, [], faces) # 頂点座標と各面の頂点の情報でメッシュを作成
obj = bpy.data.objects.new(name, msh) # メッシュデータでオブジェクトを作成
bpy.context.scene.collection.objects.link(obj) # シーンにオブジェクトを配置
# ここから下で作成(初期値name="involute_gear", m=1, b=10, alpha_deg=20, z=40, x=0, t_len = 10, x_csw=False, rho_sw=False)
実行例
# 存在するオブジェクトを削除
clear()
# m=1.5,b=15の歯車を作成
create(m=1.5, b=15)
コメント
分からないことがあったら参考文献にあるリンクを見てみてください!大体のことは載っていると思います。コメントも気軽にどうぞ!!
参考サイト・資料
- 歯車 | ライブラリ | OPEO 折川技術士事務所 (及びそのサブセクションのほとんど)https://opeo.jp/library/onepoint/mech_elem/gear/
- JIS B 4350 https://kikakurui.com/b4/B4350-2002-01.html
- 歯車を描く https://qiita.com/chromia/items/629311346c80dfd0eac7
- 「機械系 教科書シリーズ 4 機械設計法」の歯車に関するページ