歯車ってカッコいいですよね。大小ざまざまな歯車が組み合わさって連動して動いている時計のムーブメントなんて、いくらでも眺めていられる気がします。
記事の目的
歯車をプログラミングで描いてみます。歯車の種類はいろいろありますが、平歯車に絞ってチャレンジします。上の画像にあるような、我々一般人が歯車と聞いて最初に思い浮かぶタイプの歯車です。上のような、それっぽい感じの歯車が、それっぽくかみ合っているアニメーションを生成するところがゴールです。
一応世界標準のISO規格を意識した上で進めますが、準拠と言うにはほど遠い、「なんちゃって歯車」です。
歯車を作る
まずは歯車を1つ描いてみることにします。
必須の3要素
さて、平歯車を作るにあたって、決めなければいけないところは多々ありますが、最も大事なのは以下の3点です。
- m: モジュール(歯のサイズ)
- z: 歯の数
- α: 圧力角
それぞれ順番に説明していきます。
モジュール
ISOで定められている、歯車の歯のサイズを決定する単位のことをモジュールと言います。記号としてはmを用いるようです。m=1やm=5のようにして、歯車の種類を表します。
mの値が大きくなるほど、歯が大きくなります。以下に、歯の数が20のとき、m=1,2,5,10の歯車を並べてみます。
このように、mの値と歯、そして歯車自体の大きさが連動します。
歯数
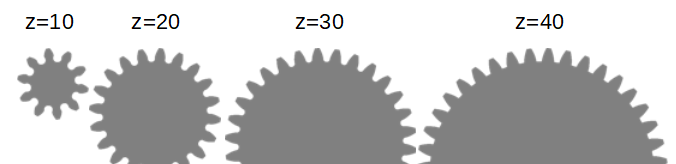
そのまんま、歯車についている歯の数を意味します。これは歯車のサイズに影響します。モジュールの値がm=5のとき、歯数z=10,20,30,40の歯車を並べてみます。
mの値は同じなので、歯の形は一緒です。数の分だけ歯を並べるため、zの値が大きいほど歯車のサイズは大きくなっていきます。歯が少ないと、歯の根元がえぐれた感じになって脆くなるので、あまり良くないようです。
歯車がかみ合うにはモジュールの値、つまりmが一致していなければならないので、歯車の大小は基本的に歯数で調節することになります。
圧力角
圧力角は歯の傾きを表す角度の値(degree)です。記号はα(アルファ)を用います。どう違うのかは説明しづらいので、次の図を見てください。m=20, z=40として、α=14.5, 17.5, 20.0の場合を並べます。
少しわかりにくいかと思いますが、歯の先っちょの太さ、歯の根元の形状、そして歯の傾斜の角度が少し変わっているのが見て取れると思います。現代の工業では圧力角20.0度の歯車が主流だそうですが、実用目的でなく、ビジュアル先行で歯車をデザインする場合は圧力角についても考慮した方がいいかもしれませんね。結構見た目の印象が変わると思います。
4つの円
m,z,αの3つのパラメータが決まると、歯車の形状をおおよそ表す4つの円を描くことができるようになります。
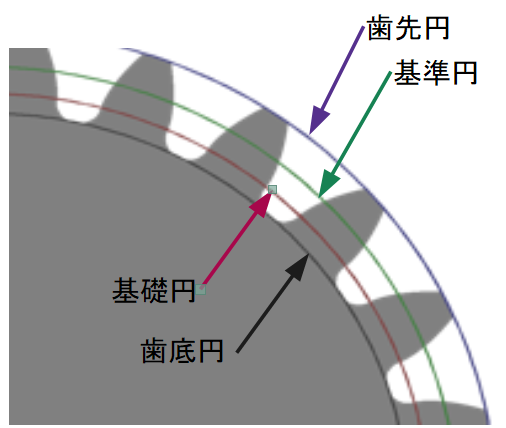
- 歯先円 : 歯の先端を囲む一番外側の円
- 基準円 : 他の3つの円の基準となる円。ピッチ円ともいう
- 基礎円 : インボリュート曲線(後述)の基礎となる円
- 歯底円 : 歯車の本体を除いて一番低い位置を表す円
この4つの円を使って歯の形を描いていくことになります。でもまあ、そこまで難しい話ではありません。
歯先円と歯底円は完全に見たまんまなので説明は省くとして、基準円と基礎円についてもう少し詳しく解説します。
基準円
基準円は他の3つの円を算出する際に用いられます。まず、基準円の直径dpについては以下のように決まっています。
d_p = zm
そして、歯先円の直径dk、歯底円の直径df、基礎円の直径dbについては以下のようになります。
\begin{align}
d_k &= d_p + 2m \\
d_f &= d_p - 2.5m \\
d_b &= d_p\ cos(\frac{2πα}{360})
\end{align}
実際に計算を行う際は直径ではなく、半径を使うので求めておきます。半分にするだけですけれども。
\begin{align}
r_p &= d_p / 2 = \frac{zm}{2} \\
r_k &= d_k / 2 = \frac{d_p}{2} + m \\
r_f &= d_f / 2 = \frac{d_p}{2} - 1.25m \\
r_b &= d_b / 2 = \frac{d_p\ cos(\frac{2πα}{360})}{2}
\end{align}
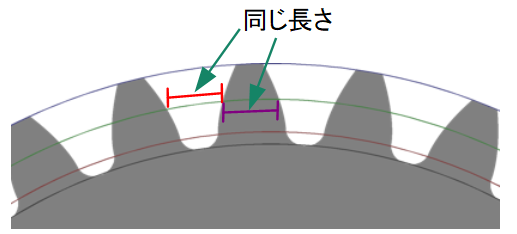
基準円の特徴はもう一つあり、次の図に示すように、円周のうち、半分が歯車の中で、半分が歯車の外にあることです。
この紫の部分の弧長を「歯厚」と呼びます。記号はsを用います。円周の長さは直径のπ倍に等しく、また上図の赤と紫の合算は円周の1/zに等しいので、
2s = \frac{d_{p}π}{z} = πm \\
s = \frac{πm}{2}
となりますね。この値は後で使います。
基礎円
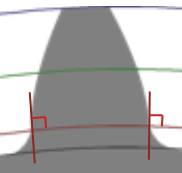
基礎円の特徴は、この円と歯が垂直に交わることにあります。
基礎円と歯が垂直に交わるポイントからそれぞれ外側と内側で、歯の曲線のつくりが切り替わります。つまりは、ここを基準にして、外と内、別々にパーツを作成するというわけです。
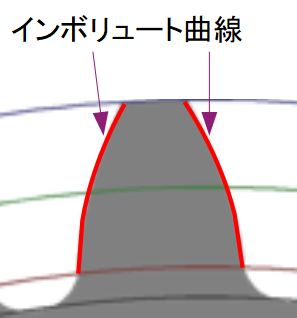
外側の歯を構成する曲線にはいろいろな種類がありますが、現在最も使用されているのはインボリュート曲線です。今回はこのインボリュート曲線を使用して歯を作成します。
歯の外側 - インボリュート曲線を描く
インボリュート曲線については検索すればいくらでも優れた資料が出てくるので、ここでは特に解説しません。
とりあえず、以下の式で必要な数値が計算できればOKです。
α = cos^{-1}\frac{r_b}{r} \\
inv\ α = tan\ α - α \\
x = r\ cos(inv\ α) \\
y = r\ sin(inv\ α)
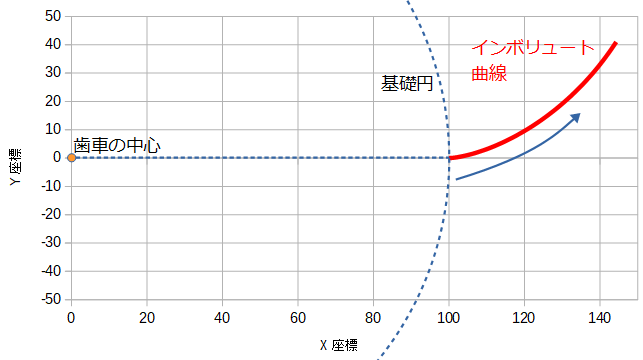
ここで、rというのは歯車の中心からの距離を表しています。インボリュート曲線を描くときは、基礎円から歯先円までを描くので、半径rbから半径rkまで少しずつrを増加させつつx,yを求めることになります。
inv αというのはインボリュート関数と呼ばれている関数です。
理解を深めるために、試しにrb=100として、グラフに表してみると以下のようになります。
| r | inv α(radian) | inv α(degree) | x | y |
|---|---|---|---|---|
| 100 | 0.000 | 0.000 | 100.000 | 0.000 |
| 105 | 0.010 | 0.591 | 104.994 | 1.083 |
| 110 | 0.029 | 1.636 | 109.955 | 3.141 |
| 115 | 0.051 | 2.946 | 114.848 | 5.910 |
| 120 | 0.078 | 4.448 | 119.639 | 9.307 |
| 125 | 0.106 | 6.102 | 124.292 | 13.287 |
| ... |
rの値をrbから始めて、少しずつ増やしながらx,yを計算します。上の表だと5刻みですが、これは流石に粗すぎるので、実際には0.5とか、0.1とか、もっと細かく刻みます。そうすると、少しずつ弧を描きながら傾きが大きくなるインボリュート曲線が出来上がります。あとはrがrk(歯先円)に達するところで計算を打ち切れば、それだけで歯の曲線が完成します。
片側の曲線を描く
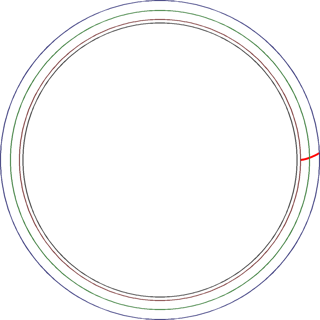
上の説明に合わせて、実際の歯車上に歯の片側の線を描いてみます。m=10,z=30として、rb=140.95の歯車とします。
4つの円と合わせて描いてみるとこんな感じになりました。なお、1単位あたり1ピクセル換算です。
……毛が生えたみたいで、しょっぼい感じですね。
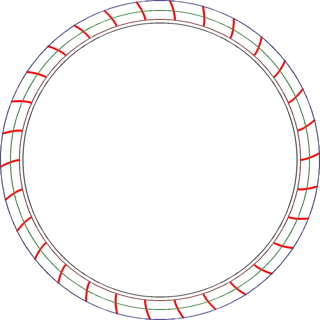
次はこれを歯数の分だけ回転したコピーを作成します。歯の数はzで、1周は2π(radian)なので、歯1つあたりの角度は2π/zですから、それぞれの曲線の座標(xi, yi)は次のように求められます。
\begin{align}
\begin{pmatrix}
x_i \\
y_i
\end{pmatrix}
&=
\begin{pmatrix}
cos\frac{2πi}{z} & -sin\frac{2πi}{z} \\
sin\frac{2πi}{z} & cos\frac{2πi}{z}
\end{pmatrix}
\times
\begin{pmatrix}
x \\
y
\end{pmatrix} \\
&=
\begin{pmatrix}
x\ cos\frac{2πi}{z} - y\ sin\frac{2πi}{z} \\
x\ sin\frac{2πi}{z} + y\ cos\frac{2πi}{z}
\end{pmatrix}
\quad (0 \leq i \lt z)
\end{align}
少し歯車っぽくなってきましたね。
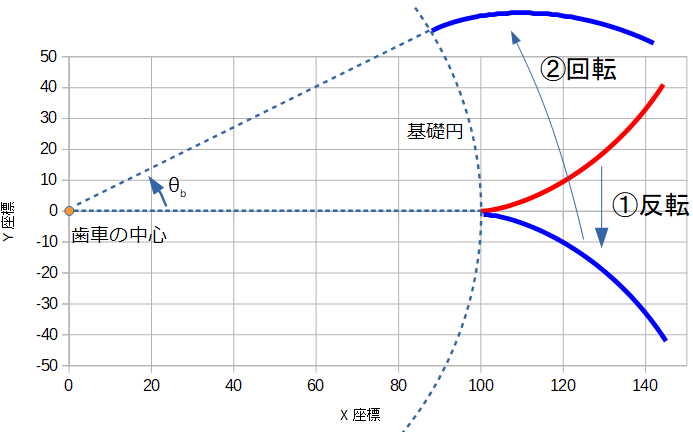
反対側の曲線を描く
片方が描けたので、次は反対側を描きたいです。作業手順のコンセプトは次のようになります。
- 元のインボリュート曲線をY軸反転したものを用意する
- それを
θb回転させて配置する
コンセプトは非常に簡単ですが、問題は「②のθbって、どれくらい?」という問題が生じます。いろいろググって調べたのですが、説明している資料が見当たらなかったので、やむなく自分で計算することにしました。
結論から言うと
θ_b = \frac{s}{r_p} + 2\ inv\ α
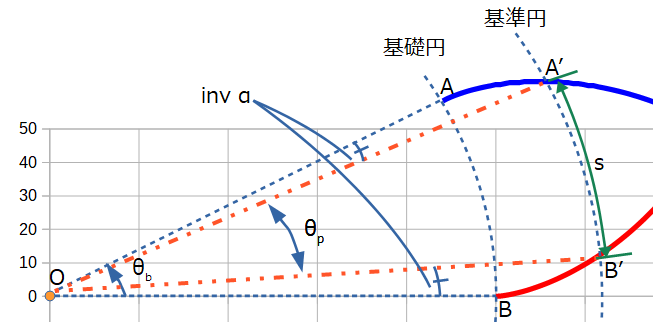
で求めることができます。sは前に求めた「基準円上の歯厚」、inv αはインボリュート関数、そしてαは圧力角の設計値(単位はradian)です。
円と歯が交差している部分の長さを歯厚と呼びます。緑色のラインで表される円弧A'B'の長さが歯厚sです。この円弧の両端と、歯車の中心を結んだとき、切り取られる扇形A'OB'について考えます。高校数学で登場する「円弧の長さ」の公式によれば、図中θpの角度は円弧の長さsと半径rpより求められます。
s = r_p\ θ_p \\
θ_p = \frac{s}{r_p}
再び図を確認し、θpとθbの差を考えると、パッと見て∠AOA'と∠BOB'がそれだとわかると思います。そして、この値は実のところ、インボリュート関数inv αで得ることができます。インボリュート関数というのは「インボリュート曲線が伸びていくと、中心からの偏角がどれだけ変化するか」というのを表す関数なので、
\begin{align}
θ_b - ∠AOA' - ∠BOB' &= θ_p \\
θ_b - 2\ inv\ α &= θ_p
\end{align}
よって
\begin{align}
θ_b &= θ_p + 2\ inv\ α \\
&= \frac{s}{r_p} + 2\ inv\ α \\
&= \frac{π}{z} + 2(tanα - α)
\end{align}
やっとθbが得られたので、反対側のインボリュート曲線を描画してみます。
大分歯車らしくなりましたね!あと一息です。
歯元部を描く
次は基礎円から内側の部分を作ります。この部分は相手の歯車と接触しない、むしろ接触してはいけない部分となっています。
ただし、ここからは「このように作るのだ」という資料が見当たらないため、私オリジナルの方法となります。何かいい情報をお持ちでしたらご教示くださいませ。
(案1)垂直に切り出す
特に何も考えず、インボリュート曲線の根元から、歯底円に向けて垂直に線を下ろします。そして、歯底円の2点を無理やりつないでしまいます。
計算式は省略します。赤と青の下端の点は計算済みなので、あとはrf/rbの比を使うなどして歯底円上の点は算出容易だと思います。
シュッとした感じの歯車になりますね。細かいことを言うと、歯底円の直線で結ぶよりは、歯底円の上を円弧で描く方がいいのかもしれませんが、よほど大きい歯車を描くのでなければ違いが分からないと思います。
(直角のところひび割れしそうですよね……)
(案2)スプライン曲線を使う
それっぽい感じの曲線を作るために、「この辺りを通ってほしい」という点をいくつか決めて、それらを通る曲線をスプライン補間で求めます。
例えばこんな感じにしてみます。
さっきと同じように歯底円上に垂線を下して2点を取った後、それらをつなぐ直線を3等分します。真ん中の2点と、基礎円上の2点、計4点を使ってスプライン補間します。
まあまあいい感じじゃないでしょうか。雑な計算だからちょっと底はみ出てますけど。
歯底円上の2点の距離をもっと離すようにすると、鍋底型に近づきますし、近づけると放物線に近づきます。
歯先部を作る
残りは歯先だけになりました。しかし、この部分は特にできることが少ないです。
とりあえずインボリュート曲線2つの先端を直線でつなげておけばいいと思います。
多少は歯先の形をいじってもいいかとは思いますが、歯先円から外にはみ出すと、歯車を組み合わせる時に干渉してしまう可能性が出てくるのでNGです。いくら見た目優先の「なんちゃって歯車」とは言ってもね。
完成
いままで作った部分を組み合わせて、色を塗ってみます。
左が歯元案1のタイプで、右が歯元案2のタイプです。どちらもアリじゃないですかね?いい感じにできたと思います。
あとは中心に穴を空けたり、軽量化のための肉抜きをしたり、装飾を施したり、3Dにしたり、好きなようにできると思います。
回す
歯車を作っておいて、回さないという選択肢はありませんよね?かみ合いながら回っている感じの動画が作れてようやくゴールです。
使用する歯車を決める
かみ合わせる歯車どうしは、同じモジュールmと同じ圧力角αで作った歯車でなくてはいけません。歯数zは好きに設定します。
2020/05/14追記
歯車zの数値は自由ですが、busyoumono99様にコメントいただいた通り、リアル歯車においては2つの歯車の歯数は互いに素(最大公約数が1)とするのが原則となっています。例えば両方の歯車が同じ歯数だと、かみ合うのはいつも同じ歯どうしになってしまい、片方の歯の1つが尖っていた場合、対の歯だけがどんどん削られて壊れてしまいます。互いに素にすることで、歯の組み合わせがずれていくため、壊れるのをなるべく遅らせることができます(ダメージ分散)。
CGとして動かすだけの場合、そういった配慮は不要ではありますが、この原則に従っておくとよりリアルな機構となるでしょう。
中心距離
歯車がかみ合うようにするには、それぞれ歯車をどのくらいの距離で配置する必要があるでしょうか。その数値は「中心距離」という数値で導き出せます。
a = \frac{d_{p1}+d_{p2}}{2} = r_{p1} + r_{p2}
単純に2つの歯車の基準円半径を足すだけですね。この距離だけ空けて2つの歯車を配置したら、歯車がかみ合って見えるように、歯車の角度を手作業で微調整します。この微調整量も計算で出せるはずですが、面倒なのでやめておきます。
回転速度
2つの歯車の速度比が適切に保たれていないと、かみ合ったまま回っているように見えてくれません。
\frac{z1}{z2} = \frac{ω2}{ω1}
歯車1と歯車2の角速度の比は、歯車1と歯車2の歯数の比の逆数に等しい。つまり、歯車1の歯数が歯車2の歯数の倍であれば、角速度は歯車2の半分でなければならない、ということです。
ω2 = \frac{z1ω1}{z2}
歯車1の角速度ω1を適当に決めて、上の式から歯車2の角速度ω2を求めればいいでしょう。
あと、回転方向は互いに逆になります。
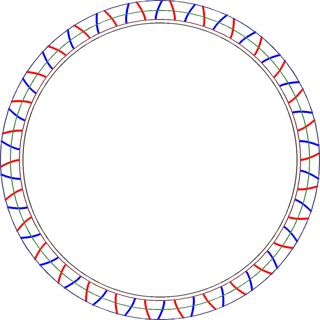
完成したアニメーション
作成した歯車をPNGで出力し、Pygameで画像を回転させるプログラムを書き、それを画面録画ソフト(OBS Studio)でMKV形式で録画し、GIFに変換(openAvitoGif)して編集(VirtualDub)しました。なんかチラついてますが気にしないでください。
少し隙間が大きいような気もしますが、まあ及第点じゃないでしょうか。
ソースコード
ソースコードはPythonで記述しました。整理したら随分長くなってしまったので、Githubに置きました。
https://github.com/chromia/figgear
| ファイル名 | 説明 |
|---|---|
| gear.py | 歯車の形状データを生成するmake_gear_figure関数と画像を生成するmake_gear_image関数を実装しています。また、コマンドラインからパラメータを指定するだけで歯車画像が簡単に作成できます |
| gear_anim.py | 5つの歯車が回転するサンプル(この記事の一番最初の画像のもの)です。Pygameを使っています |
必要なライブラリ
- Numpy
- SciPy
- Pillow
- Pygame
python -m pip install numpy scipy pillow pygame
使い方
# gear.py 出力画像ファイル名 モジュール番号m 歯数z [オプション]
python gear.py sample.png 8 20
# 色を変えたい場合は -r -g -b オプションを用いる
python gear.py sample.png 8 20 -r=255 -g=0 -b=0
# 輪郭のアンチエイリアス処理を行うには --ssaa オプションを用いる
python gear.py sample.png 8 20 -r=255 -g=0 -b=0 --ssaa=4
# 中央に穴を空ける
python gear.py sample.png 8 20 --draw-center-hole=true --center-hole-size=0.2
# その他のオプションについては -h または --helpで
python gear.py -h
自分でソースコードを書いて使う場合。
生データが欲しい場合はmake_gear_figure関数を使います。
from gear import make_gear_figure
# make_gear_figureの使い方
help(make_gear_figure) # 使い方に関する説明を表示する
m = 20 # モジュール
z = 30 # 歯数
alpha = 20.0 # 圧力角
bottom_type = "spline" # 歯底の形状 "spline"または"line"
points, blueprint = make_gear_figure(m, z, alpha, bottom_type)
for x, y in points: # pointsには歯車形状を表す点列が得られる
print(x, y) # この点を順番につなぐと、歯車の外周ができる
for k, v in blueprint.items(): # blueprintには各種寸法が入っている
print(k, v)
とりあえず画像が欲しい場合はmake_gear_image関数を使います。
from gear import make_gear_image
# make_gear_imageの使い方
help(make_gear_image) # 使い方に関する説明を表示する
m = 10
z = 30
alpha = 20.0
# 最初の3つの引数(出力ファイル, モジュール, 歯数)は固定で、あとはオプションとして指定する
# ただしハイフンは使えないので、アンダーバーに置き換えが必要
# 指定できるオプションについてはpython gear.py -hを参照のこと
make_gear_image("sample.png", m, z, alpha=alpha, ssaa=4,
draw_center_hole=True, image_margin=10)
make_gear_image("sample2.png", m, z) # オプションを指定しない場合は初期値が使われる
# 引数を羅列すると長くなりすぎるので可変長引数を使う方法がスマート
options = {"alpha": alpha,
"ssaa": 4,
"draw_center_hole": True,
"image_margin": 10}
make_gear_image("sample3.png", m, z, **options)
io.BytesIOなどを使えば実ファイルに書き出さず、インメモリで使用することもできます。gear_anim.pyを参考にしてください。
参考資料
今回説明した内容はおおむね小原歯車工業株式会社様の公開されている資料の受け売りでした。分かりやすくかつ膨大な情報の提供、深く御礼申し上げます。
特に上記URLの「歯車ABC 基礎編」と「歯車技術資料」は基礎の基礎から計算式まで記載してあって、ものすごいありがたい資料でした。
JISの歯車用語の定義も役に立ちました。作りたい部位の名前をこれで調べて、あとはWeb検索にかけるという手法に便利でした。
JISC - 日本産業標準調査会 ※「B0102-1」(歯車用語-第1部:幾何形状に関する定義)で検索
終わりに
もっと簡単に作れるのかな、と思っていましたが、めちゃくちゃ専門用語の数が多くて、情報の荒波を漂う感じで調査が大変でした。結局まだ分からないところも多いままで、奥の深い世界だと実感しました。
遊星歯車とか、かさ歯車とか、より複雑で面白そうな歯車もあるので、いずれは挑戦してみたいですね。