本シリーズでは、「FXの予測プログラム」を作りながら、機械学習・ディープラーニングを解説します。
(注)のび太くんは有名漫画のキャラとは一切関係ありません。
この物語は、大学生のび太くんが、家庭教師のすぐるさんから機械学習を学び、将来D-mind社を起業して、汎用人工知能搭載型ロボットを誕生させる記録です。
前回のお話
前回は「if文で翌日のFX(為替)を予測する作戦」を実行してみたものの、失敗に終わったのび太くんでした。
第1話:のび太、if文でFXを予想する
本日は、家庭教師のすぐるさんから、「線形モデルによる回帰」を学びます。
第2話:のび太、線形回帰を学ぶ
すぐるさん、最近「犬型ロボット」が予約発売されたんだって。
ぼくも欲しいな~
22世紀には「しゃべる猫型ロボット」も生まれるかもしれないね。
しゃべる猫・・・
ぼくは、かわいい犬の方がいいな。
さて、のび太くん、今日は線形モデルによる回帰をやってみようか。
最初に線形回帰モデルを説明をし、後半に練習問題で実装をしてみよう。
線形モデル?
「線形モデル」というのは、単純な掛け算と足し算だけで作られる「モデル」のことだよ。
う~ん、まず、その「モデル」っていうのが分かんないよ。
そうだね。すまない。
少し整理しようか。
今回予測したいものを、「翌日の終値 - 当日の終値」とするね。
この予測したい「翌日の終値 - 当日の終値」を
$y_p(t)$
と書くことにしよう。
$p$って何?
$p$はprediction(予測)のpだよ。
続いて、予測に使う材料を$x$で表すことにしよう。
予測の材料には何を使うの?
それはとても難しい質問だね。
はっきり言って、答えはない。
!!!教えてくれるって言ったじゃないか!!
完璧な答えはないけど、だいたいは分かるよ。
要は、翌日の終値に影響しそうなものを使えばいいんだよ。
う~ん、影響しそうなもの・・・
あんまり、FXや為替が分からないから、何が影響しそうか分からないよ。
そうだね。そのあたりは、社会人になるにつれ、経済を学べば分かるようになるよ。
とりあえず今回は、「ドル円の、当日から過去25日分の終値」、25個の値を予測に使う材料としよう。
どうして25個なの?
FXは平日のみ行われているから、25日分でだいたい1か月分のデータになるんだよ。
つまり、1ヶ月前までのデータ25個から、
「翌日の終値が、当日の終値に対していくら変化するのか」
を予測することになる。
今回の場合、その予測のための「式」や「手法」を、「モデル」と呼ぶんだよ。
う~ん、なんとなく分かったよ。
でも線形ってどういう意味?
よしまずは、今回作るモデルを見てみようか。
今回作り上げるモデルは次の式で表される。
y_p(t)=w_{1}x_{1}(t)+w_{2}x_{2}(t)+\cdots +w_{N}x_{N}(t)+b
この$y_p(t)$が、実際の結果
$y(t)=(t+1日の終値)-(t日の終値)$
と、同じになると、うまく予測できたことになる。
$x_1(t)~x_N(t)$は、予測に使う入力データだよ。
今回は$x_1(t)$は$t$日の終値、$x_2(t)$は$t-1$日の終値・・・
という感じで、$t$日を基準に、$N-1$日前までの終値を表しているよ。
そして、$w_{1}~w_{N}$が、今回求めたい線形モデルの係数だよ。
のび太くん、ここまでは大丈夫?
・
・
・
むにゃむにゃ・・・
のび太くん、起きて!!
まだ$y$と$w$と$x$が出てきただけだよ。
難しいよ。数式とか分からない・・・
大丈夫だよ。ゆっくり説明するから。
この式を見ても、$x$の○乗とか、expとか、難しそうなものがない。
y_p(t)=w_{0}x_{0}(t)+w_{1}x_{1}(t)+\cdots +w_{N}x_{N}(t)+b
ただの「かけ算と足し算」だろう。
こういうのを線形モデルっていうんだよ。
う~ん・・・
ベクトルで書くとすっきりして、分かりやすくなるよ。
\mathbf{x}(t)=(x_1(t), x_2(t)\cdots x_{N}(t))^T
\mathbf{w}=(w_1, w_2,\cdots w_{N})^T
と書くことにするね。
ベクトルか~。なんか勉強したような・・・
終わりにある$T$は?
終わりにある$T$は転置(Transpose)という意味だよ。
本当は縦方向のベクトルを書きたいんだけど、書きにくいから横方向に書いて、転置してねって意味だよ。
すると、元の線形モデルは、次のように書かれるよ。
y_p(t)=\mathbf{w}^T\mathbf{x}(t)+b
ベクトルだと、すっきりしただろ。
ベクトルで書いたときに、$\mathbf{y_p}$と$\mathbf{x}$が、この式の形で書き表されるモデルを、「線形モデル」と呼ぶんだ。
うん、分かった。そういうことにするよ。
・
・
・
でも、$\mathbf{w}=w_0~w_{N}$と、$b$はどうやって決めるの?
それが今回の問題だよ。
そこが決まれば、予測モデルの完成だからね。
そのために、「学習データ」を使用するんだ。
今回は2007年から2016年のデータを「学習データ」としよう。
この学習データを使用して、最もうまく予想できる$w_0~w_{N}$と$b$を決定するんだよ。
そして、求めた$w_0~w_{N}$と$b$で、2017年のデータを「テストデータ」として推定し、どれくらいうまく予測できるかを確かめるんだ。
とりあえず学習データを使って、$\mathbf{w}$と$b$を求めるってことは分かったよ。
・
・
・
う~ん、でも、どうやって2007年から2016年のデータから、$w_0~w_{N}$と$b$を決めるの?
それをこれから説明しよう。
$\mathbf{w}$と$b$を求めるために、次の式のように、「予測と実際の値の誤差の2乗和」を書き表すんだ。
E(\mathbf{w}, b)=\sum_{t=0}^{M}\left [ {y(t)-y_p(t)} \right ]^2=\sum_{t=0}^{M}\left [ {y(t)-\left \{\mathbf{w}^T\mathbf{x}(t)+b \right \}} \right ]^2
$t=0$が2007年の初日、$t=M$が2016年の最後の日を表しているよ。
$E$は誤差(Error)という意味だ。
損失(Loss)を使用して、$L$で書かれることもあるよ。
今回は掛けていないけど、$\frac{1}{2}$を掛けていることも多いよ。
この誤差関数$E$は$\mathbf{w}$と$b$の関数となっていて、$\mathbf{w}, b$を入力として、モデルの「予測誤差の2乗和」を出力することになる。
ここまでは分かったかい?
・
・
・
もう一回言って。
よし。$\mathbf{w}$と$b$を求めるために、予測の誤差の2乗和を求めるんだ。
E(\mathbf{w}, b)=\sum_{t=0}^{M}\left [ {y(t)-y_p(t)} \right ]^2=\sum_{t=0}^{M}\left [ {y(t)-\left \{\mathbf{w}^T\mathbf{x}(t)+b \right \}} \right ]^2
$t=0$が2007年の初日、$t=M$が2016年の最後の日を表している。
$E$は誤差(Error)という意味だ。
この誤差関数$E$は$\mathbf{w}, b$の関数となっていて、$\mathbf{w}, b$を入力として、モデルの予測誤差を出力することになる。
どうだい、分かったかい?
どうして、引き算の結果を2乗しないといけないの?
面倒だし、したくないな~
2乗しないと、誤差が0, 0の場合も、1, -1の場合も、足すと0になってしまうだろ。
だから2乗するんだ。
じゃあ、4乗でも6乗でも良いってこと?
それは良い質問だよ。そういう好奇心がとても大切だ。
実はそれを理解するのは、いまの、のび太くんでは難しい。
でも、あえて言っておくね。
この線形モデルの誤差は、様々な小さな誤差の集まりでできていると考えると、中心極限定理により、モデルの誤差が正規分布を描くと想定できる。
すると、データ$y$が生成される$\mathbf{w}, b$を最尤推定で求めると、正規分布の対数尤度を求めることになり、2乗和が出てくるから、今回は2乗和を使うんだよ。
うん、分かんないや。
まあ、最尤推定の話をしたときに、またこの話はしよう。
考えてみれば、4乗より2乗の方が簡単そうだし、ボクは2乗でいいや。
とりあえず、誤差の2乗和$E$が最小となる$(\mathbf{w}, b)$を求めるってことは分かったよ。
E(\mathbf{w}, b)=\sum_{t=0}^{M}\left [ {y(t)-y_p(t)} \right ]^2=\sum_{t=0}^{M}\left [ {y(t)-\left \{\mathbf{w}^T\mathbf{x}(t)+b \right \}} \right ]^2
・
・
・
でも、どうやって、$E$から$(\mathbf{w}, b)$を求めるの?
ここで、微分、正しくは偏微分が出てくる。
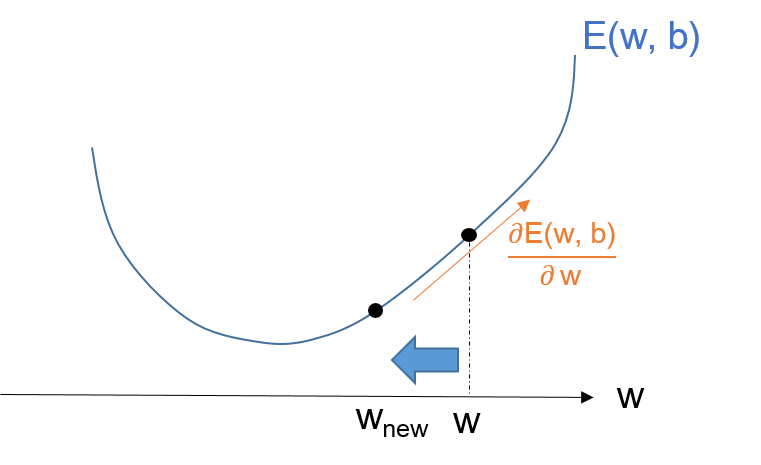
誤差が最小ということは、求めたい$(\mathbf{w}, b)$の値のときに、$E$が最小値、つまり谷の形の底の部分になる。
そして、適当な$(\mathbf{w}, b)$の値で、$E$の偏微分を求めると、そのベクトルは、その谷底の逆方向を示している。
なぜなら微分(偏微分)というのは、傾きが最も大きくなる方向と、その傾きの大きさを示すからね。
偏微分か・・・
う~ん、まあそういうものだと思うことにするよ。
最初はそれで良いよ。
まず適当に$(\mathbf{w}, b)$を決めてあげる。
そして、$(\mathbf{w}, b)$のそれぞれで$E$の偏微分を求めたベクトルの逆方向、すなわちマイナス方向に、$(\mathbf{w}, b)$を更新するんだ。
式で書くと次の通りだよ。
\mathbf{w}_{new} = \mathbf{w}-\eta \frac{\partial }{\partial \mathbf{w}}E(\mathbf{w}, b)
b_{new} = b-\eta \frac{\partial }{\partial b}E(\mathbf{w}, b)
ここで$\eta $は、学習率と呼ばれる小さな値だよ。
一気に$(\mathbf{w}, b)$を更新すると、谷底を行き過ぎてしまうかもしれないからね。
少しずつ更新してあげるんだ。
この更新を繰り返せば、いつか$(\mathbf{w}, b)$は、谷底の値になり、誤差関数の出力(誤差の2乗和)も最小になるんだ。
このように、偏微分を使って、少しずつ更新する方法を「勾配降下法」と呼ぶんだよ。
今回の式の場合は「最急降下法」とも呼ばれるよ。
なんとなくイメージはついたよ。
微分したら、谷底の方向が分かるから、少しずつ、そこに近づけるんだね。
・
・
・
でも、この偏微分を計算する部分が良く分からないや。
この偏微分の計算は、落ち着いてやれば手計算でできるよ。
ちなみに線形回帰の場合は、勾配降下法を使わなくても、一気に谷底の$(\mathbf{w}, b)$を計算することができる。
でも一気に谷底の値が分かるのは、今回くらいだ。
それに、実際にプログラムを書くときには、ライブラリの関数が行ってくれるから、偏微分のコードを自分で書くことはないよ。
なんだ、良かった♪
でも、きちんとプログラムが背後で何をやっているのかを理解しておくことは大事だからね。
じゃあ、今日は最後に練習問題として、自分で線形モデルを構築して、解いてみるコードを実装してみよう。
もう、疲れたよ。
最後の一息だよ。頑張ろう!
分かったよ。
これもiPhone Xへの一歩だ。
線形回帰モデルを機械学習で実装
今回のコードは全部僕のGitHubにおいて置くね。
本記事の掲載コードはこちら
最初はいつものおまじないゾーンだ。
って言っても、これから使うライブラリを宣言しているだけだよ。
# import関連
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pylab as plt
import seaborn as sns
import warnings
warnings.filterwarnings('ignore') # 実行上問題ない注意は非表示にする
%matplotlib inline
よし、それじゃあ、自分で問題を作ろう。
今回は$w_1=1.0$、$w_2=2.0$、$b=3.0$というモデルが先にあったとする。
このモデルから学習データと、テストデータを作成しよう。
# 練習問題: 問題を作成
from numpy.random import * #乱数のライブラリをimport
X_train = rand(100,2) # 0〜1の乱数で 100行2列の行列を生成
X_test = rand(100,2) # 0〜1の乱数で 100行2列の行列を生成
# 係数を設定
w1 = 1.0
w2 = 2.0
b = 3.0
# モデルからの誤差となるノイズを作成
noise_train = 0.1*randn(100)
noise_test = 0.1*randn(100)
Y_train = w1*X_train[:,0] + w2*X_train[:,1] + b + noise_train
Y_test = w1*X_test[:,0] + w2*X_test[:,1] + b + noise_test
うん、できたよ。
よし、じゃあ、これからしたいことを整理しよう。
分かっているのは、$Y_{train}$と$X_{train}$、そして、$Y_{test}$と$X_{test}$だよ。
つまり、$Y_{train}$と$X_{train}$の間にある線形モデルを求めて、その後、$X_{test}$から、$Y_{p}$を求めるってことだよね。
その通り!
そして$Y_{p}$が$Y_{test}$と、ほぼ一緒の値になると予測成功だ。
線形回帰モデルの係数を求めるライブラリはいろいろあるけど、
Pythonnの代表的な機械学習のライブラリであるscikit-learnを使用しよう。
# 練習問題: 問題を線形回帰モデルで解く
from sklearn import linear_model # scikit-learnライブラリの関数を使用します
linear_reg_model = linear_model.LinearRegression() # モデルの定義
linear_reg_model.fit(X_train, Y_train) # モデルに対して、学習データをフィットさせ係数を学習させます
print("回帰式モデルの係数")
print(linear_reg_model.coef_)
print(linear_reg_model.intercept_)
出力:
回帰式モデルの係数
[ 1.01672273 1.93190578]
3.02237850998
だいたい、出力が1、2、3になったよ!!
うん、これは学習データから、うまくモデルが推定できたことを表しているよ。
といっても、今回は、1、2、3から作ったという情報があるから分かるけど、
実際の問題では、この係数からだけではうまくいっているかは分からない。
テストデータから予測してみて、結果を比べてみよう。
# グラフで予測具合を見る
Y_pred = linear_reg_model.predict(X_test) # テストデータから予測してみる
result = pd.DataFrame(Y_pred) # 予測
result.columns = ['Y_pred']
result['Y_test'] = Y_test
sns.set_style('darkgrid')
sns.regplot(x='Y_pred', y='Y_test', data=result)
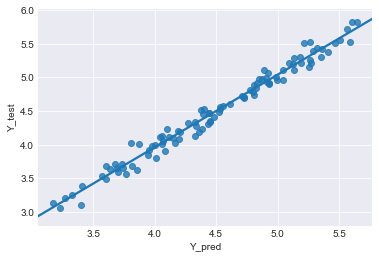
横軸がモデルから予測した値、縦軸が実際の値だよ。
この直線は点の近似直線だ。
横軸と縦軸の値がだいたい一緒になってるよ!
うん、近似直線も$y=x$の形になっていて、傾きがほぼ1になっているね。
この結果は、$Y_{p}$が$Y_{test}$と、ほぼ一緒の値になったことを示している。
つまり、学習データ$Y_{train}$と$X_{train}$を使用して、きちんと予測モデルを作れたことを示しているよ。
ちなみに、今回使用したlinear_model.LinearRegression() は、
勾配降下法でなく、一気に谷底の値を求めているよ。
ふ~、やっとできたのか。
これで練習問題は終了だ。
のび太くんも「線形回帰モデル」が使えるようになったね。
う~ん、分かったような・・・
もう疲れたよ。
僕も今日はもう疲れたから、次回、実際のFXデータで線形回帰をしてみよう。
ただ覚えておいて欲しいのは、線形回帰はFXだけでなく、ビジネスのいろいろな場面で使われるんだよ。
例えば、来期の生産量を決定するために、長期天気予報や過去のデータから、製品の需要を予測することもできる。
いろいろ便利なんだね。
次回は、いよいよFXデータで線形回帰をしてみよう。
うん!
・
・
・
次回:「線形モデル回帰分析で、FXを予測」に続く
以上、ご一読いただきありがとうございます。
「ここが分かりにくいよ~不明」など、気軽にコメントください。
可能な限り、加筆修正して、分かりやすくしたいです。
また、記事やコードの間違え、改善点、不明点、感想なども
気軽にコメントいただければ幸いです。
感謝