第1章 識別と生成
深層学習(ディープラーニング)は、識別と生成の2つにモデルを分けることができる。
機械学習のモデルは基本的に確率を使って判断する。
1.1 識別モデルと生成モデル
1.1.1 識別モデル
データを目的のクラスに分類する
基本的にデータ量の多いものから、データ量の少ないものを作るモデル
画像:3000px×2000pxのデータ ⇒ 膨大な数字のデータ
犬や猫のクラス:多くても数千種類 ⇒ 高々数千のデータ
例:画像(データ)を入力すると、犬や猫(クラス)と識別する
犬や猫の画像⇒データ、犬、猫⇒クラス
ある身長のひとは、どのくらいの体重?
”あるデータ $x$ が与えられた”という条件のもとでクラス$C_k$ である(条件付き)確率は($k$は種類)
$$P(C_k|x)$$
画像等の高次元なデータから、犬や猫という種類(クラス)の確率のように低次元のデータを出力するため、必要な学習データは生成モデルより少ない。
1.1.2 生成モデル
識別モデルの逆で特定のクラスのデータを生成する。
データ量の少ないものから、データ量の多いものを作るモデル
実際は、生成モデルを使って識別モデルを作ることができる。
犬という特定のクラス(1種類)から犬っぽい画像(データ)を出力。
その際、一番確率の高いものを出力する。
特定のクラスのデータを生成する。
例)犬の画像がどういったものかを学習し、犬の画像を生成(クラスを入力とし、画像を出力)
条件「あるクラス$C_k$ 」に属する」という条件のもとでのデータ$x$ の分布。
$$P(x|C_k)$$
犬、猫などのクラス(種類)のように低次元データから、犬っぽい、猫っぽい画像のように高次元なデータを出力するため、必要な学習データは識別モデルより多く必要となる。
学習データが多くなると、必要なコンピュータの計算量(使用量)や学習にかかる時間が多くなる。
| 識別モデル | 生成モデル |
|---|---|
| 決定木 | 隠れマルコフモデル |
| ロジスティック回帰 | ベイジアンネットワーク |
| サポートベクターマシン(SVM) | 変分オートエンコーダ(VAE) |
| ニューラルネットワーク | 敵対的生成ネットワーク(GAN) |
| ↓(応用) | ↓(応用) |
| 画像認識など | 画像の超解像、テキストの生成など |
変分オートエンコーダ(VAE)と敵対的生成ネットワーク(GAN)は深層学習のモデル。
特に最近、敵対的生成ネットワーク(GAN)は、研究が盛んで、
アイドルの顔を作ったり、CGモデリングを自動にしたりしている。
ズームをした時に画像が悪くなるので、生成モデルを使って画像をよくする(画質の向上)。
GoogleのBERTを使って言語生成をする。
1.1.3 万能近似定理
ニューラルネットワークのような活性化関数をネットワークを使うことで
どんな関数でもうまいこと近似できることを保証するための定理
それまでは、人間が何かしら関数を作っていた。
ノーフリーランチの定理
あらゆる問題で性能の良い汎用最適化戦略は理論上不可能
全て問題に対して高性能なアルゴリズムは存在しない
1.2 ニューラルネットワークの全体像
ニューラルネットワークは、入力層(何かしらのデータ)、中間層(いい感じで計算してくれる層)、出力層からなる。
ニューラルネットワークは、重み$w$とバイアス$b$を調整して、よい出力結果を出す変換器である。
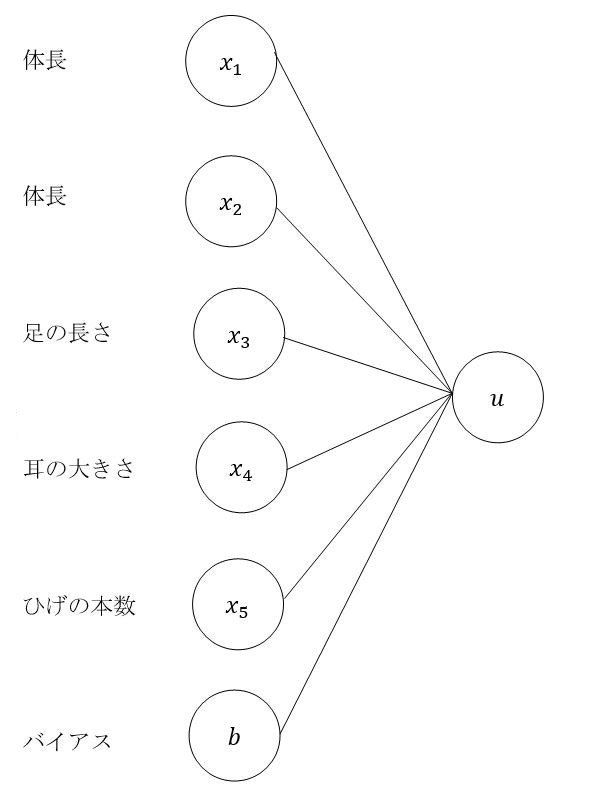
入力層:身長、体重、ひげの本数、毛の平均長、耳の大きさ、眉間、足の長さ
出力層:犬、猫、ネズミ
1.2.1 用語の説明
入力層:説明変数を入力する
中間層:入力層をもとに何かしらの重み$w$とバイアス$b$を学習する
出力層:最終的な結果(分類でいう、犬、猫、ネズミの確率など)を出力する
誤差関数:目的変数と予測値の比較を行う関数。
ノード:ニューラルネットワークの1つ1つ(よくあるニューラルネットワークの図における丸で表されるもの)こと。
確認テスト1
1.ディープラーニングは、結局何をやろうとしているか2行以内で述べよ。
回答:ふつうは何かの処理をするときは、プログラマーがプログラムを書く。
ディープラーニングはプログラムを書く代わりに、中間層を用いて入力値から出力値に変換する数学モデルを構築する。
2.次の中のどの値の最適化が最終目的か。
①入力値、②出力値、③重み、④バイアス、⑤総入力、⑥中間層入力、⑦学習率
回答:③重み[$W$]と④バイアス[$b$]
確認テスト2
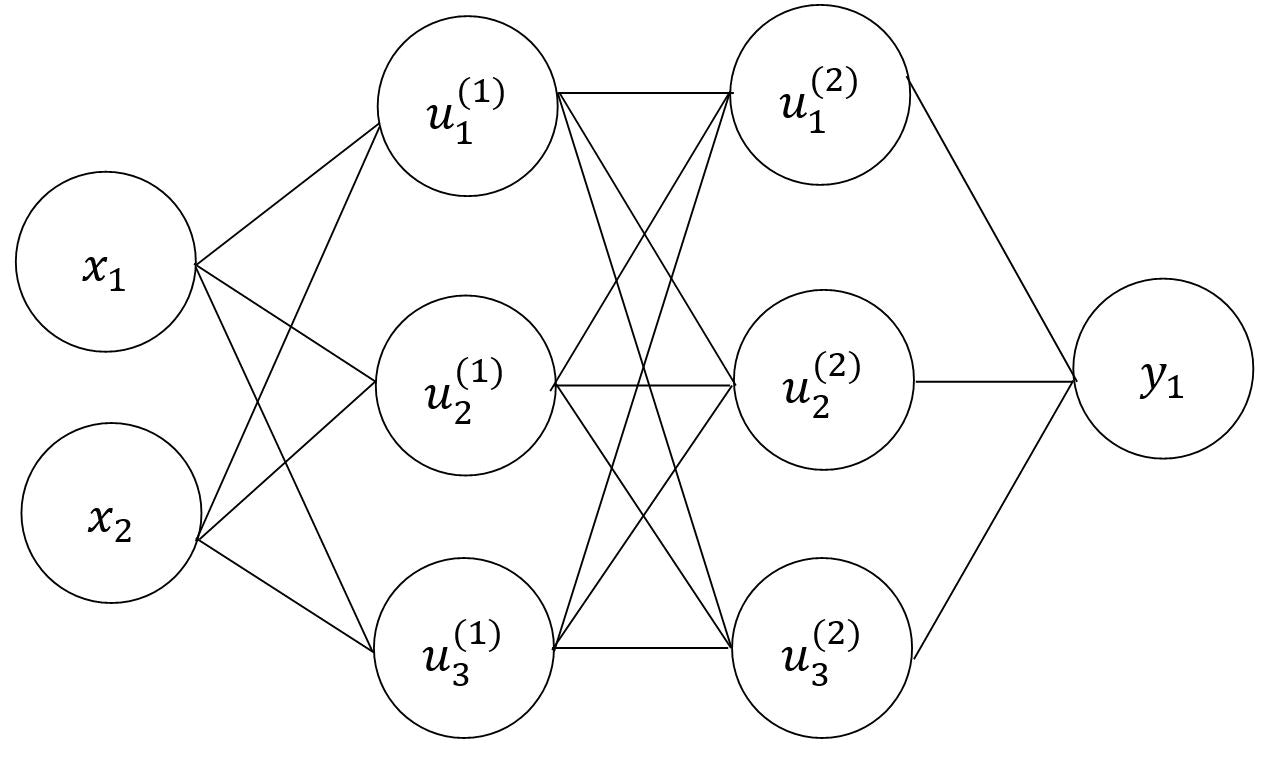
以下のニューラルネットワークを紙に書け。
入力層:2ノード1層
中間層:3ノード2層
出力層:1ノード1層
答
1.2.2 ニューラルネットワーク(NN)でできること
回帰(連続的なつながりがあるものの予測)
結果予想(例:身長の予想、体重の予想、売上予想、株価予想)
ランキング予想(例:競馬順位予想、人気順位予想)
分類(とびとびのデータを予測)
猫写真の判別
手書き文字認識(0,1,2…という数字の画像を読み取って、何の数字なのかを判定)
花の種類分類
1.2.3 ニューラルネットワーク:回帰
連続する実数値を取る関数の近似。
| 回帰分析 | 分類分析 |
|---|---|
| 連続する実数値を取る関数の近似 | 離散的な結果を予想する |
| (具体的な手法↓) | (具体的な手法↓) |
| 線形回帰 | ベイズ分類 |
| 回帰木 | ロジスティック回帰 |
| 決定木 | |
| ランダムフォレスト | ランダムフォレスト |
| ニューラルネットワーク | ニューラルネットワーク |
ニューラルネットワークは回帰の問題にも、分類に問題にも使える。
参照:万能近似定理
1.3 深層学習の実用例
一般に、ニューラルネットワークの中で、
4つ以上中間層があるものを深層ニューラルネットワークという。
中間層が増えることで、より複雑な問題に対処できる。
(数字から数字に変換がニューラルネットワーク)
自動売買(トレード)・・・時系列データ
⇒ある瞬間の全銘柄を入力にとり、ある1分後の1社の株価を予測する
チャットボット
頑張って数字を文章に置き換え、置き換えた数字をニューラルネットワークで処理し、答えとなる文章を出力する。
文章も1種の時系列データ
翻訳
チャットボットと同じ、
音声解釈(音声認識)
音声はある瞬間の空気の振動を計測することで、数値に変換できる。
音声データは数値として入力できる。
音声を数値として扱うことで、文字列を出力できる。
囲碁、将棋AI
がんばって数値の並びに置き換える。
ニューラルネットワークで学習できる。
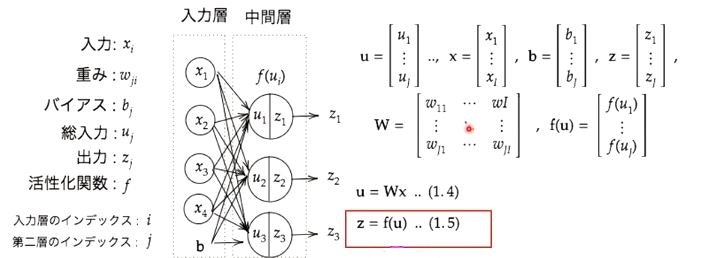
5.入力層~中間層
\begin{eqnarray}
u&=&Wx+b \\
z&=&f(u)
\end{eqnarray}
説明変数と重みの内積+バイアスの結果を活性化関数に入力して出力(ここでは中間層の出力なので次の層への入力となる)を得る。
$x_i$:入力(説明変数)
$w_i$:各説明変数に対する重み($x_i$が重要なら、$w_i$が大きい。傾き)
$b$:バイアス(1次関数で言う切片)
$u$:総入力
$z$:出力
$f$:活性化関数
学習によってパラメータ$w$と$b$を最適化していく。
6.3.確認テスト3
入力層~中間層の図式に動物分類の例を入れる。
確認テスト
以下の数式をPythonで書け。
$$u=w_1x_1+w_2x_2+w_3x_3+w_4x_4+b=Wx+b$$
答
import numpy as np
u = np.dot(x, W) + b
第2章 活性化関数
活性化関数はニューラルネットワークにおいて、次の層への出力の大きさを決める非線形の関数
次の層への値を伝えるか伝えないか、またはその強弱を定める
確認テスト
線形と非線形の違いを簡潔に説明せよ。
答:線形は直線、加法性と斉次性を満たす。
非線形は直線以外、加法性もしくは斉次性を満たさない。
加法性
$$f(x+y)=f(x)+f(y)$$
斉次性
$$f(kx)=kf(x)$$
2.1 中間層に用いられる活性化関数
2.1.1 ステップ関数
現在、活性化関数として用いられることは少ない
あるところまで何も反応しない、あるところで一気に反応する
(on/offしかない。)
線形分離可能なものしか学習できないため、今は使い道があまりない。
f(x)=\left\{
\begin{array}{l}
1 \qquad (x\geqq 0)\\
0 \qquad (x<0)
\end{array}
\right.
サンプルコード
def step_function(x):
if x > 0:
return 1
else:
return 0
2.1.2 シグモイド関数
0~1の間を滑らかに変化する関数。
滑らかに上昇する曲線のため微分ができるため学習がうまく進めることができる
大きな値では変化が微小のため、勾配消失問題が起きることがある。
シグモイド関数が使われたことにより、ニューラルネットワークがいろいろなことを学習できるようになった。
$$f(u)=\frac{1}{1+e^{-u}}=\frac{1}{1+\exp(-u)}$$
サンプルコード
def sigmoid(x):
return 1 / (1 + np.exp(-x))
2.1.3 ReLU関数(Reflected Linear Unit、正規化線形関数)
最も使われている活性化関数。
入力が0より小さければ0を出力し、0より大きければそのまま出力する。
勾配消失問題の回避やスパース化に貢献することで良い成果。
f(x)=\left\{
\begin{array}{l}
x \qquad (x> 0)\\
0 \qquad (x\leqq 0)
\end{array}
\right.
サンプルコード
def relu(x):
return np.maximum(0, x)
確認テスト:以下の赤枠に該当する箇所を抜き出せ(3層の部分から)
答
# 1層の総出力
z1 = functions.relu(u1)
# 2層の総出力
z2 = functions.relu(u2)
入力層、中間層、出力症の3層構造のニューラルネットワークにおける中間層の出力部分。
別のファイル(↓参照)に中身の処理が書いてある。
(commonのフォルダに入っているfunctions.pyに書いてある)
from common import functions
第3章 出力層
分類は人間が欲しい最終的な結果を出力する。
犬の確率、猫の確率、ネズミの確率のように各クラスに属する確率を出力
実際にニューラルネットワークの学習において、
入力データと訓練データ(正解値)を用意する
そして出力層の結果と目的変数の正解値を比較し、どのくらい合っているかを表現するのが誤差関数
3.1 誤差関数
例えば分類の場合、各クラスが属する確率とOne-hotベクトルで表現されている各クラスの正解値をもとにどれだけ合っているか、ズレているか算出する。
ズレているほど値は大きくなる。
課題:(平均二乗誤差で)なぜ、引き算でなく二乗するか述べよ。
答
誤差和は0になってしまうから。(ひき算して、全部足すと0になる)
各ラベルでの誤差は正負の両方の値が発生し全体の誤差を正しく表すのに都合が悪い。
2乗してすることで全てのラベルでの誤差が正の値になるようにしている。
課題:1/2はどういう意味を持つか述べよ。
答:
計算の便宜上(計算式が簡単になる。本質的な意味はない。)
次の章で学習する誤差逆伝播するときに、微分の計算が必要になる。
微分したときに、2乗の2が前に出るため1/2と相殺できる。
分類問題の場合:誤差関数 → クロスエントロピー誤差、
回帰問題の場合:誤差関数 → 平均二乗誤差(MSE)
を用いると学習がスムーズになる。
3.2 平均二乗誤差(MSE:Mean Squared Error)
回帰問題の誤差関数
def mean_squared_error(y, d):
return np.mean(np.square(y-d)) / 2
3.3 クロスエントロピー誤差(交差エントロピー誤差)
分類問題の誤差関数
def cross_entropy_error(d, y):
if y.ndim == 1:
d = d.reshape(1, d.size)
y = y.reshape(1, y.size)
#
if d.size == y.size:
d = d.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7) / batch_size
3.4 出力層の活性化関数
中間層の活性化関数は、入力された値をいい感じに情報を抽出するために変換するために用いられるが、出力層は、中間層で学習した内容を私たちが使いやすくするために用いられる。
情報を抽出するための中間層
抽出された情報を使いやすい形に過去するための出力層
回帰 → 恒等写像
ニ値分類 → シグモイド関数
多クラス分類(犬・猫・ネズミ) → ソフトマックス関数
3.4.1 シグモイド関数(ロジスティック関数)
$$f(u)=\frac{1}{1+e^{-u}}=\frac{1}{1+\exp(-u)}$$
ロジスティック回帰で用いる時と同じで2値分類で1のクラスに該当する確率を出力する。
1のクラスに該当する確率、1のクラスに該当しない確率(0のクラスに該当する確率)を合計すると1となる。
3.4.1 ソフトマックス関数
$$f(i,u)=\frac{e^{u_i}}{\displaystyle\sum_{k=1}^Ke^{u_k}}$$
3クラス以上で全部を足すと1(100%)になる。
クラス数($K$)ごとに全部足すというのがコードに含まれる。
# ソフトマックス関数
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) # オーバーフロー対策
return np.exp(x) / np.sum(np.exp(x))
確認テスト、ソフトマックス関数の
① $f(i,u)$、② $e^{u_i}$、③ $\sum_{k=1}^Ke^{u_k}$ に該当するコードを示し、説明せよ。
答:
①
# ①
return y.T
①
# ②
np.exp(x)
③
# ③
np.sum(np.exp(x),axis=0)
# ソフトマックス関数
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0) #プログラムの動きを安定させるため追加
y = np.exp(x) / np.sum(np.exp(x), axis=0) #総和(全体)np.exp(x)で割ることで、確率としている。
return y.T
x = x - np.max(x) # オーバーフロー対策(プログラムの動きを安定)
return np.exp(x) / np.sum(np.exp(x)) # この1行がソフトマックスでやりたいことのすべて
確認テスト、クロスエントロピー関数の
① $E_n(W)$、②右辺の説明
答
# クロスエントロピー
def cross_entropy_error(d, y):
if y.ndim == 1: # 1次元の場合。
d = d.reshape(1, d.size) # (1, 全要素数)のベクトルに変形する
y = y.reshape(1, y.size) # (1, 全要素数)のベクトルに変形する
# 教師データが one-hot-vector の場合、正解ラベルのインデックスに変換
if d.size == y.size:
d = d.argmax(axis=1) # argmaxで最大値のインデックスを取得
batch_size = y.shape[0] # この場合は行の形状なので1
return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7) / batch_size #分子まで(/ batch_size)が本質的な部分
# ごく小さい値を加えることで0に落ちない処理をしている
# np.arangeでバッチサイズ分取り出して対数関数に与えている。
第4章 勾配降下法の種類
4.1 勾配降下法の種類
勾配降下法は、ニューラルネットワークを学習させる手法で3種類ある。
・勾配降下法
・ミニバッチ勾配降下法
・確率的勾配降下法(SGD)
4.2 再掲 深層学習の目的
深層学習の目的は、誤差 $E(w)$ を最小化するパラメータ $w$ を発見すること。
重みやバイアスを見つけていく。
4.3 勾配降下法の数式
$$w^{(t+1)}=w^{(t)}-\varepsilon \nabla E$$
学習は何回も何回も行う。
前回の答えたところから間違えた部分を引く $-\varepsilon \nabla E$
調整して、次回に活かすのが学習のコンセプト。
全回間違えた部分を如何に生かすか?が、係数にある学習率$\varepsilon$
学習率がちょうどいい値だと、学習がスムーズ
$$\nabla E=\frac{\partial E}{\partial w}=\left[\frac{\partial E}{\partial w_1},\cdots ,\frac{\partial E}{\partial w_M}\right]$$
確認テスト:$w^{(t+1)}=w^{(t)}-\varepsilon \nabla E$に該当するコードを探す。
network[key] -= learning_rate * grad[key]
4.4 学習率
学習率が大きいと、最適解(最小値)を飛び越えて値が大きくなり、学習がうまく進まない。このことを「発散」という。
逆に、学習率が小さいと発散する確率が減るが、時間がかかる。
学習率が小さいときの一番の問題は、局所最適解(極小値)を求めてしまう可能性がある。
学習率を決定する手法は次のように様々あるがAdamが一番使われる。
・Momentum
・AdaGrad
・Adadelta
・Adam
4.5 エポック
誤差関数の値を小さくする方向に重み$W$及びバイアス$b$を更新し、次の週に反映することをエポックと言う。
データセット全てを一度与えることを1エポックと言う。
例えば、同じデータセットを2回与えるなら2エポックとなる。
自然言語のモデルを作る場合wikipediaの全データを使う場合
100エポックや200エポックくらい行うと、ある程度の学習ができる。
4.6 確率的勾配降下法
$$w^{(t+1)}=w^{(t)}-\varepsilon \nabla E_n$$
・データが冗長な場合は計算コストを軽減
・毎回毎回違いデータを使って学習するため、望まない局所最適解に収束するリスクを軽減
・オンライン学習できる。
4.7 オンライン学習
全データを使ってモデルに学習を一気にするバッチ学習の逆で
モデルに都度都度データを与えて学習させる学習手法。
最初に全部データを準備する必要がない。
リアルタイムで手に入るデータについて学習できる。
バッチ学習の場合、一度に大量データをメモリ上に展開しないといけないため、
都度データを与えるオンライン学習の方がよく使われている。
確認テスト:オンライン学習とはなにか。
答:モデルにその都度データ与えて学習させる学習手法。
全データを使ってモデルに学習を一気にするバッチ学習の逆
学習データが入ってくる都度パラメータを更新し、学習を進めていく手法。
4.8 ミニバッチ勾配降下法
\begin{eqnarray}
w^{(t+1)}=w^{(t)}-\varepsilon \nabla E_n
\end{eqnarray}
オンライン学習の派生版で、オンライン学習の特徴をうまくバッチ学習に取り入れたものが、ミニバッチ勾配降下法
小分けにする小分けのことをミニバッチと言う。
メリット:確率的勾配降下法のメリットを損なわず、計算機の計算資源を有効利用できる。
CPUを利用したスレッド並列化やGPUを利用したSIMD(single Instruction Multi Data)並列化
1人のコックが1つずつ処理に対して
何人もコックがいて同時並行で処理⇒SIMD並列化
1つの機械で処理するのはコンピュータでは限界に達している。
たくさん機械を使って同時並行で処理
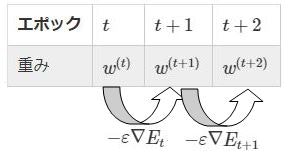
確認テスト:
$$w^{(t+1)}=w^{(t)}-\varepsilon \nabla E_n$$
を図に書く。
[](|エポック|$t$|$t+1$|$t+2$|
---|---|---|---|
|重み |$w^{(t)}$|$w^{(t+1)}$|$w^{(t+2)}$|
$-\varepsilon\nabla E_t$、$-\varepsilon\nabla E_{t+1}$)
第5章誤差逆伝播法
$$\nabla E=\frac{\partial E}{\partial w}=\left[\frac{\partial E}{\partial w_1},\cdots ,\frac{\partial E}{\partial w_M}\right]$$
どう計算する?
数値微分
$$\frac{\partial E}{\partial w_m}=\lim_{h \to 0}\frac{E(w_m+h)-E(w_m-h)}{2h}$$
このやり方では、計算量が非常に多くなってしまう。そこで、誤差逆伝播法を利用する。
数値微分の別バリエーション、数値微分ではない方法で更新量を求める。
算出した誤差を出力層側から順に微分し、前の層へとで伝播。
最小限の計算で各パラメータの微分値を解析的に計算する手法が誤差逆伝播法。
⇒ 順伝播によって算出された誤差を微分して前に戻すことで重みとバイアスを修正していく。
確認テスト:
誤差逆伝播法では不要な再帰的処理を避ける事が出来る。
既に行った計算結果を保持しているソースコードを抽出せよ。
答:
# 出力層でのデルタ
# functions.d_mean_squared_errorが誤差関数を微分したもの
delta2 = functions.d_mean_squared_error(d, y)
# b2の勾配
grad['b2'] = np.sum(delta2, axis=0)
# W2の勾配
grad['W2'] = np.dot(z1.T, delta2)
# 中間層でのデルタ
#delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1)
## 試してみよう
# 1回使った微分を使いまわしている。
delta1 = np.dot(delta2, W2.T) * functions.d_sigmoid(z1)
delta1 = delta1[np.newaxis, :]
# b1の勾配
grad['b1'] = np.sum(delta1, axis=0)
x = x[np.newaxis, :]
# W1の勾配
grad['W1'] = np.dot(x.T, delta1)
# print_vec("偏微分_重み1", grad["W1"])
# print_vec("偏微分_重み2", grad["W2"])
# print_vec("偏微分_バイアス1", grad["b1"])
# print_vec("偏微分_バイアス2", grad["b2"])
return grad
数式の流れ
\begin{eqnarray}
E(\mathbb{y})&=&\frac12\sum_{j=1}^{l}\left(y_j-d_j \right)^2=\frac12\|\mathbb{y}-\mathbb{d}\|^2\\
\mathbb{y}&=&\mathbb{u}^{(l)}\\
\mathbb{u}^{(l)}&=&\mathbb{w}^{(l)}\mathbb{z}^{(l-1)}+\mathbb{b}^{(l)}\\
\frac{\partial E}{\partial w_{ji}^{(2)}}&=&\frac{\partial E}{\partial \mathbb{y}}\times \frac{\partial \mathbb{y}}{\partial \mathbb{u}}\times \frac{\partial \mathbb{u}}{\partial w_{ji}}\\
\frac{\partial E(\mathbb{y})}{\partial \mathbb{y}}&=&\frac{\partial }{\partial \mathbb{y}}\frac12\|\mathbb{y}-\mathbb{d}\|^2=\mathbb{y}-\mathbb{d}\\
\frac{\partial \mathbb{y(\mathbb{u})}}{\partial \mathbb{u}}&=&\frac{\partial \mathbb{u}}{\partial \mathbb{u}}=1
\end{eqnarray}
入力層、中間層1つ、出力層の3層ニューラルネットワークの場合、中間層までの計算は以下のようになる(中間層から入力層へも同じ流れ)。
最終的に求めたいものは $\displaystyle\frac{\partial E}{\partial w_{ji}}$
活性化関数には恒等写像を使うことを仮定している。($\mathbb{y}=\mathbb{u}^{(l)}$)
確認テスト
$$\frac{\partial E}{\partial \mathbb{y}}\times \frac{\partial \mathbb{y}}{\partial \mathbb{u}}$$
に該当するソースコード
答:
delta2 = functions.d_mean_squared_error(d, y)
確認テスト
$$\frac{\partial E}{\partial \mathbb{y}}\times \frac{\partial \mathbb{y}}{\partial \mathbb{u}}\times \frac{\partial \mathbb{u}}{\partial w_{ji}^{(2)}}$$
に該当するソースコード
grad['W2'] = np.dot(z1.T, delta2)