本テキストは公開されている資料や開発者様から提供頂いたソースコードを基に@starfieldKtが作成しています。
そのため開発者様が意図していることと異なる部分がある可能性があることをご注意ください。
また、本テキストに関することを開発者様へお問い合わせ頂かないようお願い申し上げます。
その他格子生成ツールについてはこちら
簡易直線・蛇行水路生成ツール "Simple Straight and Meandering Channel Creator"
| 項目 | 内容 |
|---|---|
| 名称 |
Simple Straight and Meandering Channel Creator 簡易直線・蛇行水路生成ツール |
| 開発者 | 清水康行 |
| 説明 | 簡易蛇行水路格子生成ツール. 直線,サインジェネレーテッドカーブ,木下蛇行水路を簡単に作ることが出来ます. |
概要
延長、川幅、縦横断方向の格子数を指定した直線水路および、波長、波数、蛇行角、水路幅、縦横断方向の格子数を指定するサイン・ジェネレーテッド・カーブ蛇行水路を作成できるほか、蛇行水路に歪度と平坦度を設定した木下蛇行水路の作成ができる。
また、それぞれの水路形状において、上下流と中央部に直線水路を追加したり、河床形状や水路幅の変化を設定できる。
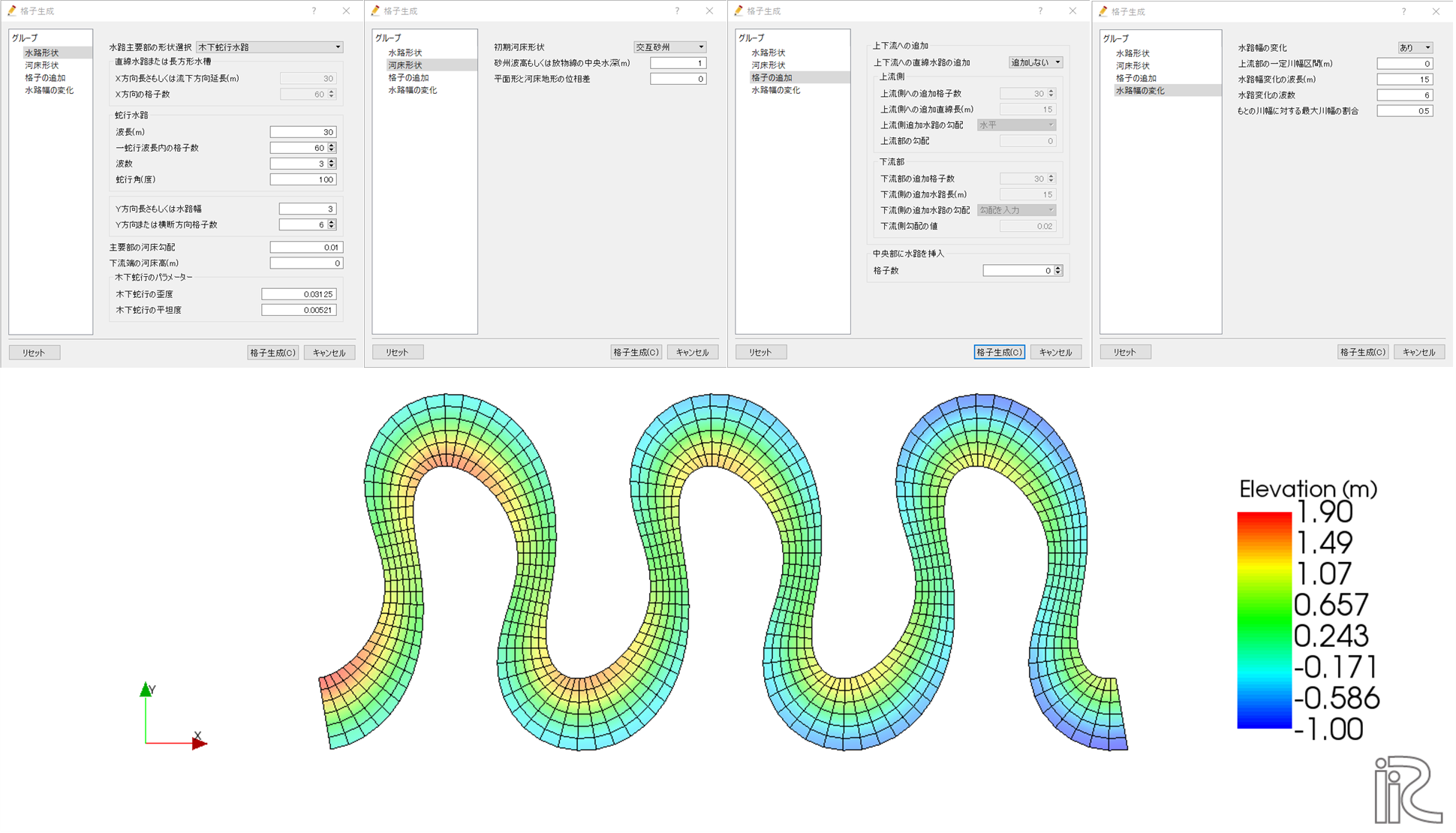
格子生成条件
水路形状
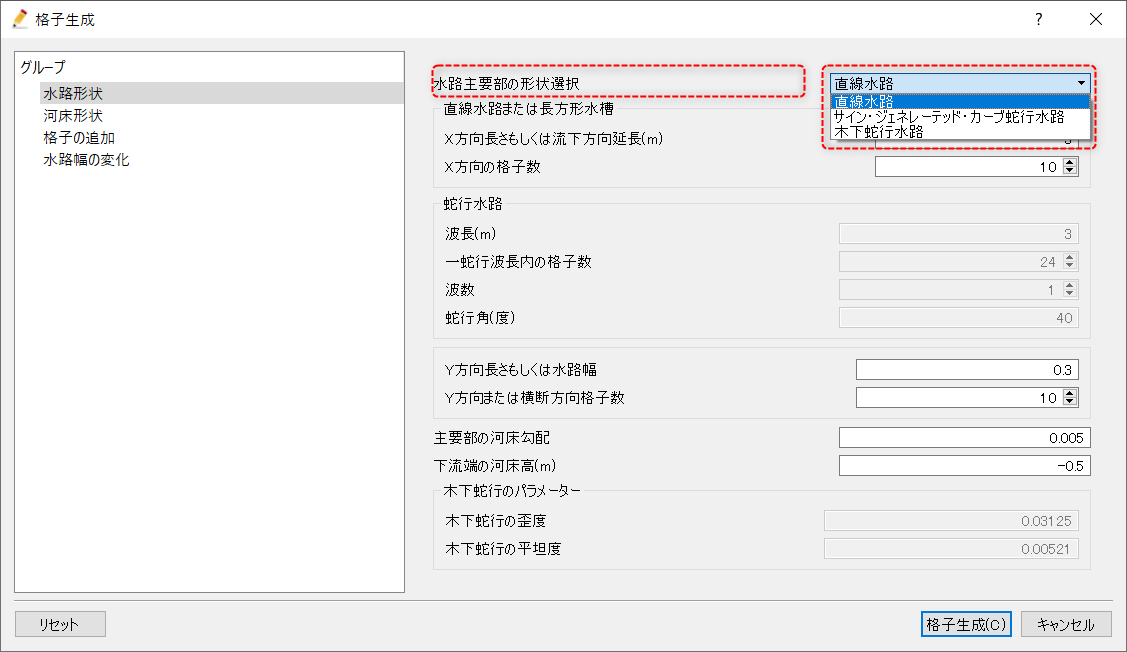
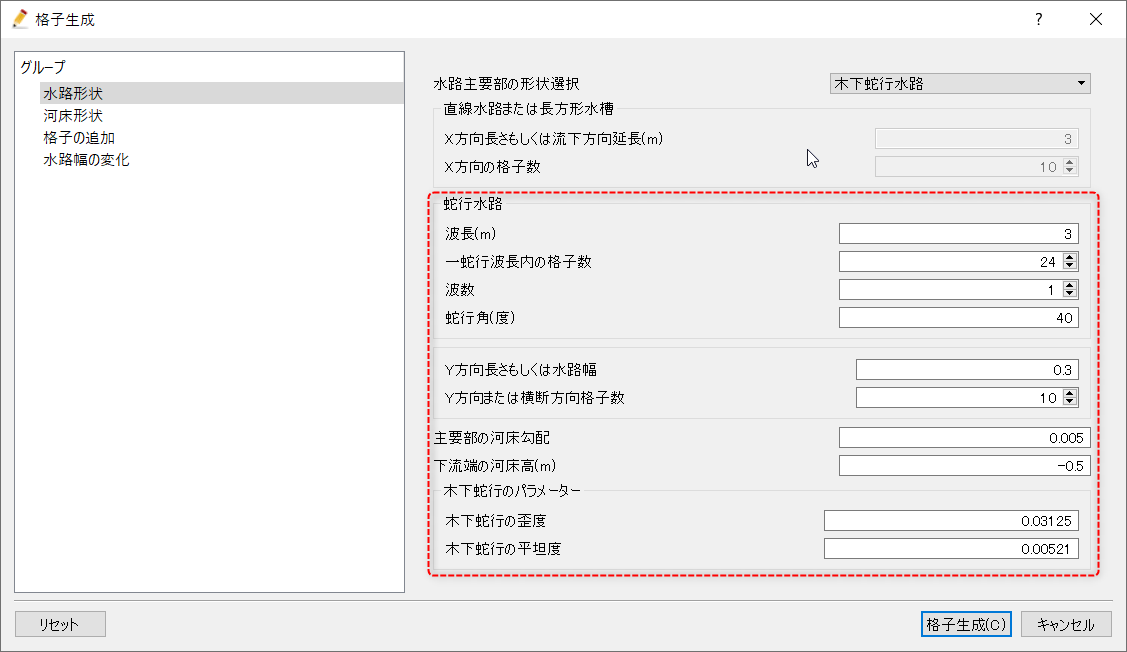
水路形状グループでは、水路主要部の形状選択の項目で何を選択するかによって入力するパラメータが異なる。
水路主要部の形状としては直線水路、サイン・ジェネレーテッド・カーブ蛇行水路、木下蛇行水路が選択できる。
なお、Y方向長さもしくは水路幅、Y方向または横断方向格子数、主要部の河床勾配、下流端の河床高(m)は水路主要部の形状にかかわらず共通の設定項目である。
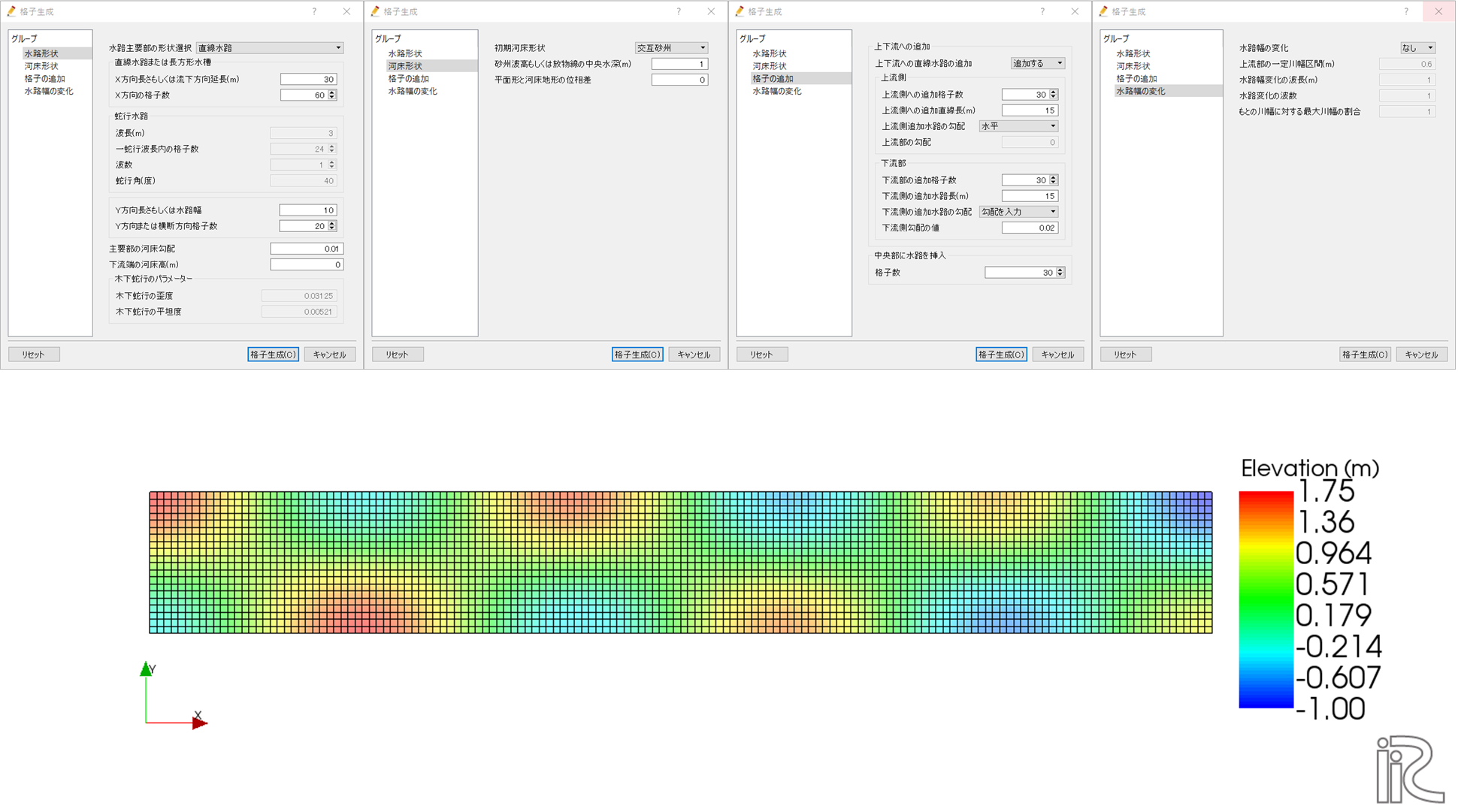
直線水路
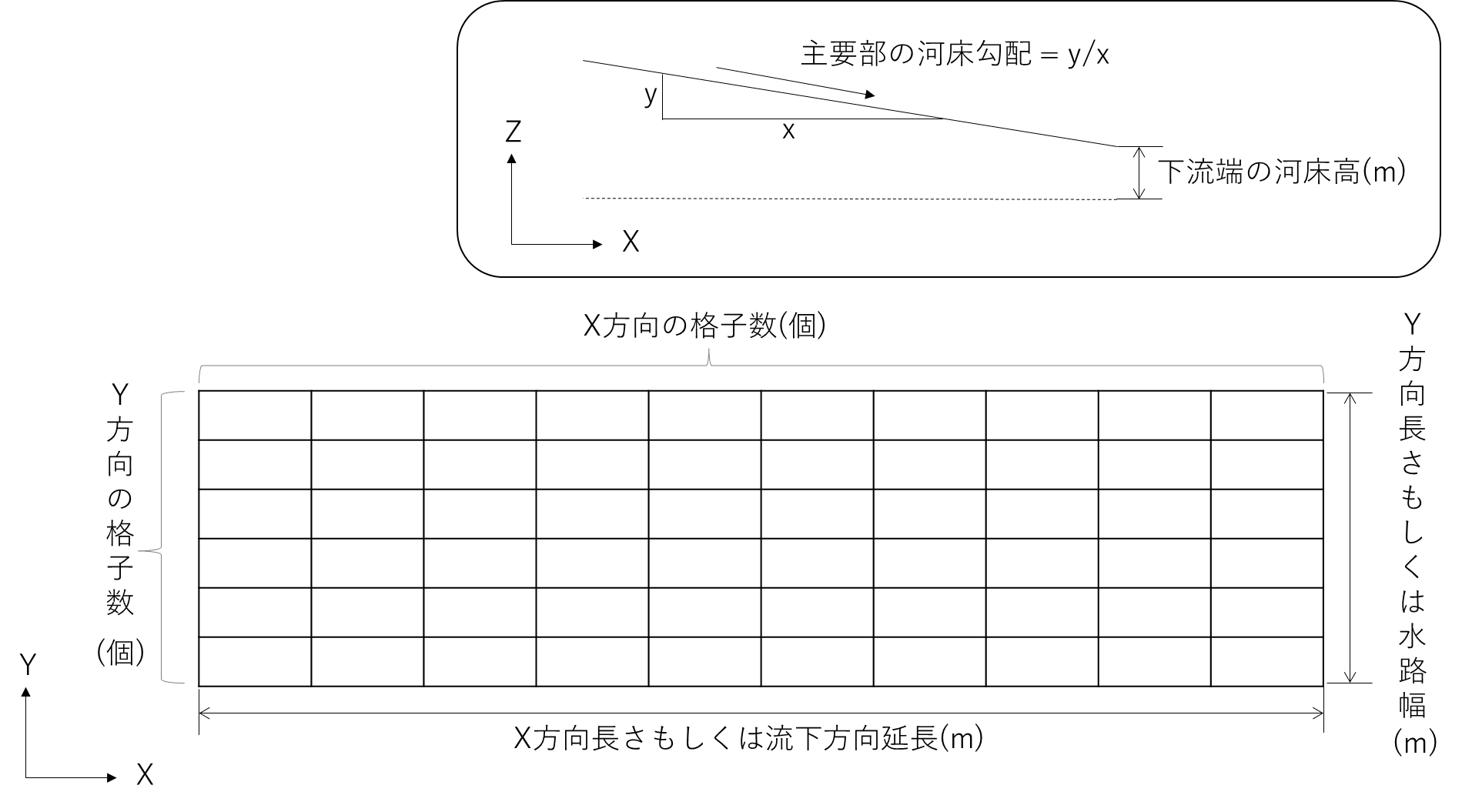
水路主要部の形状が直線水路の場合は共通項目の他に、水路のX方向長もしくは流下方向延長(m)、X方向の格子数が必要となる。
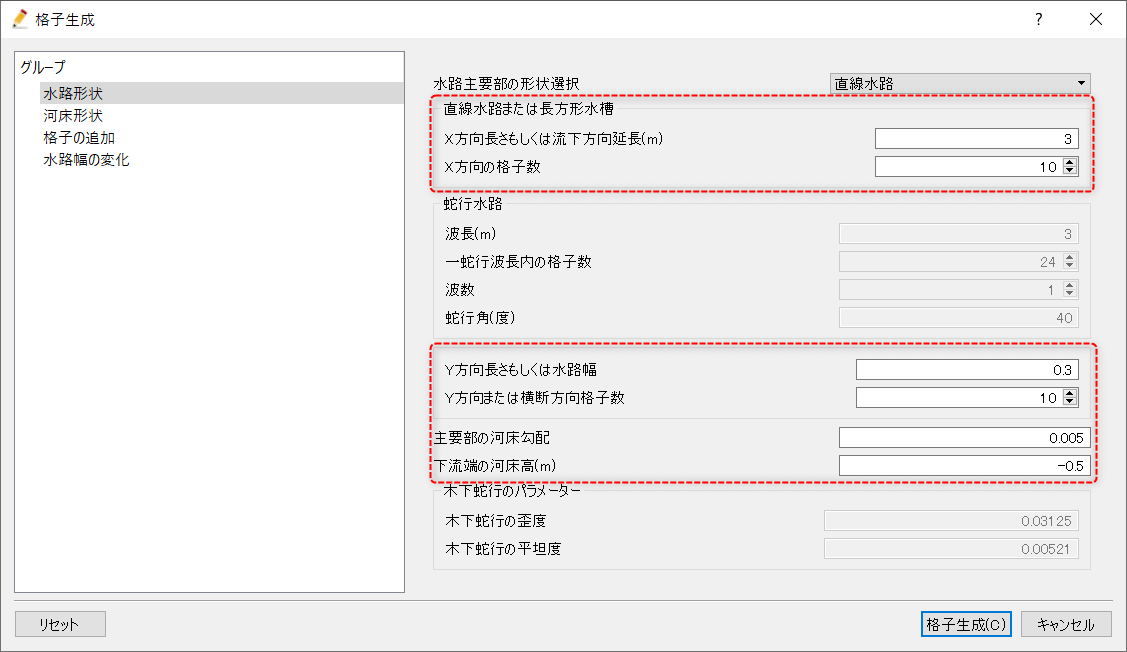
各条件のイメージはこのようになる。
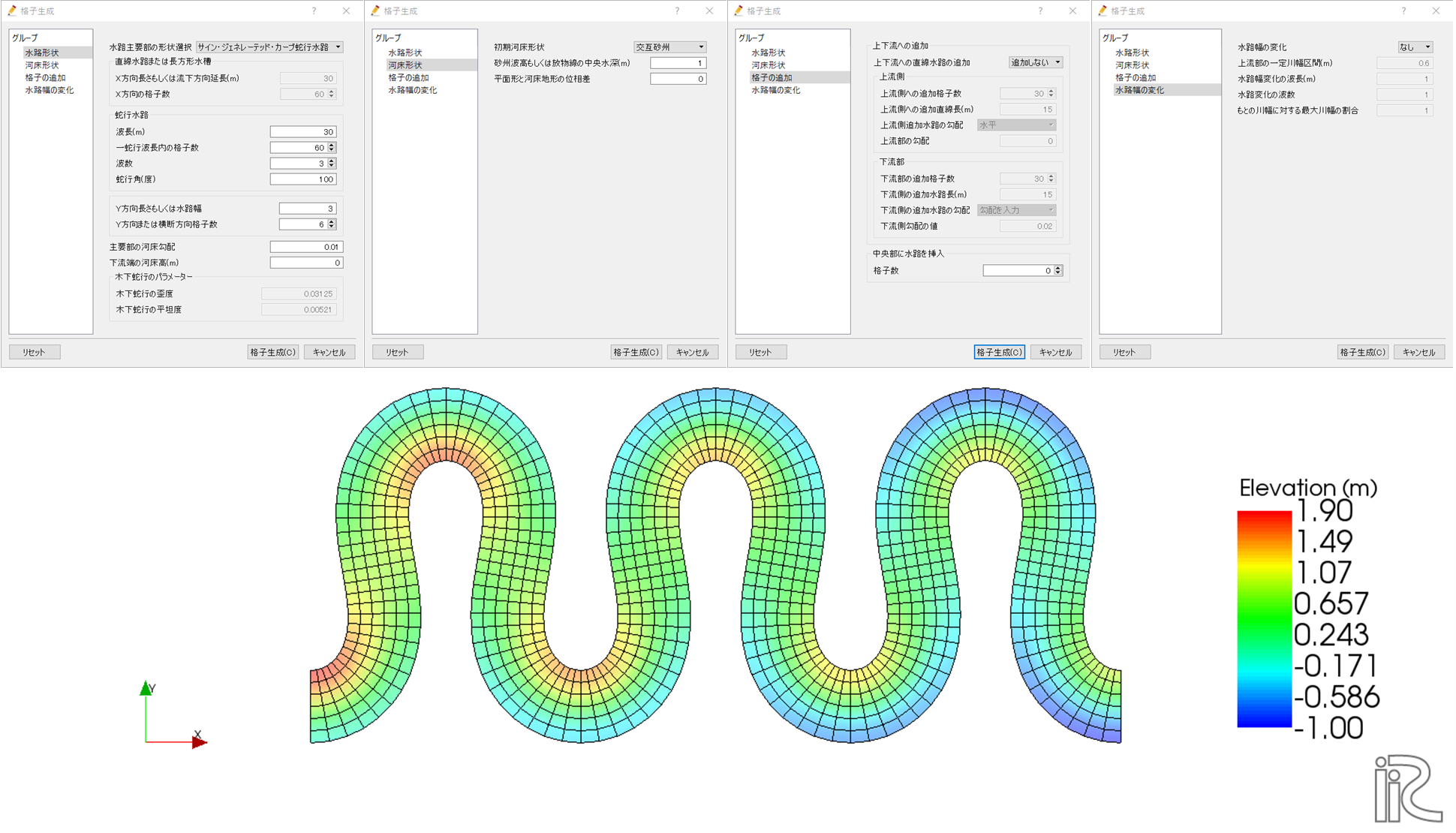
サイン・ジェネレーテッド・カーブ蛇行水路
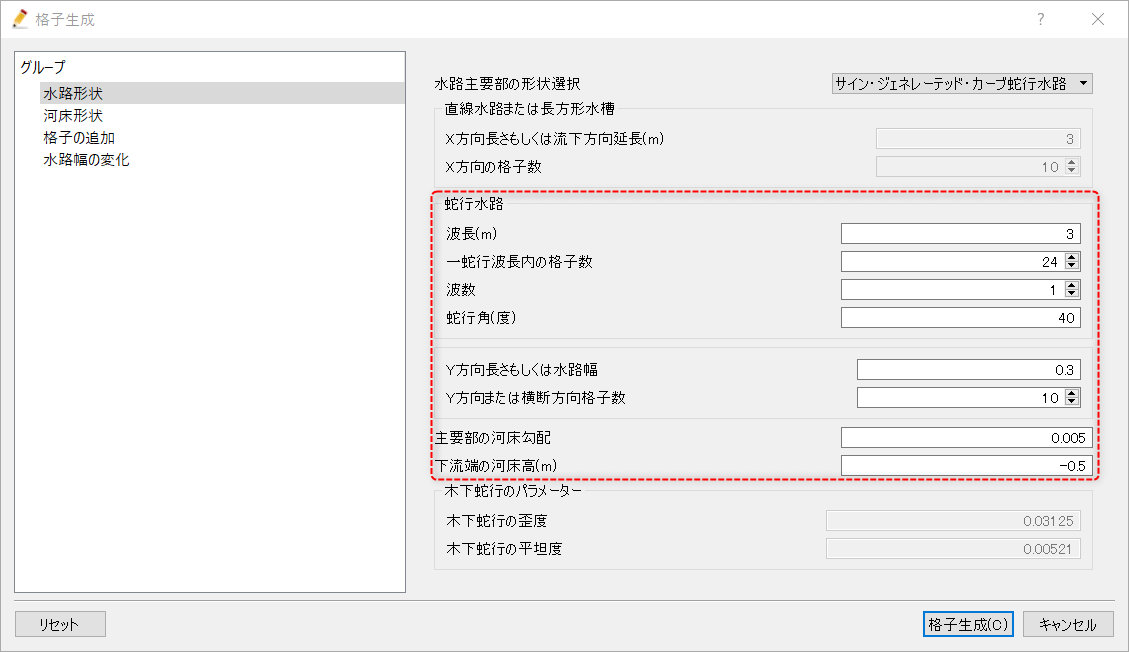
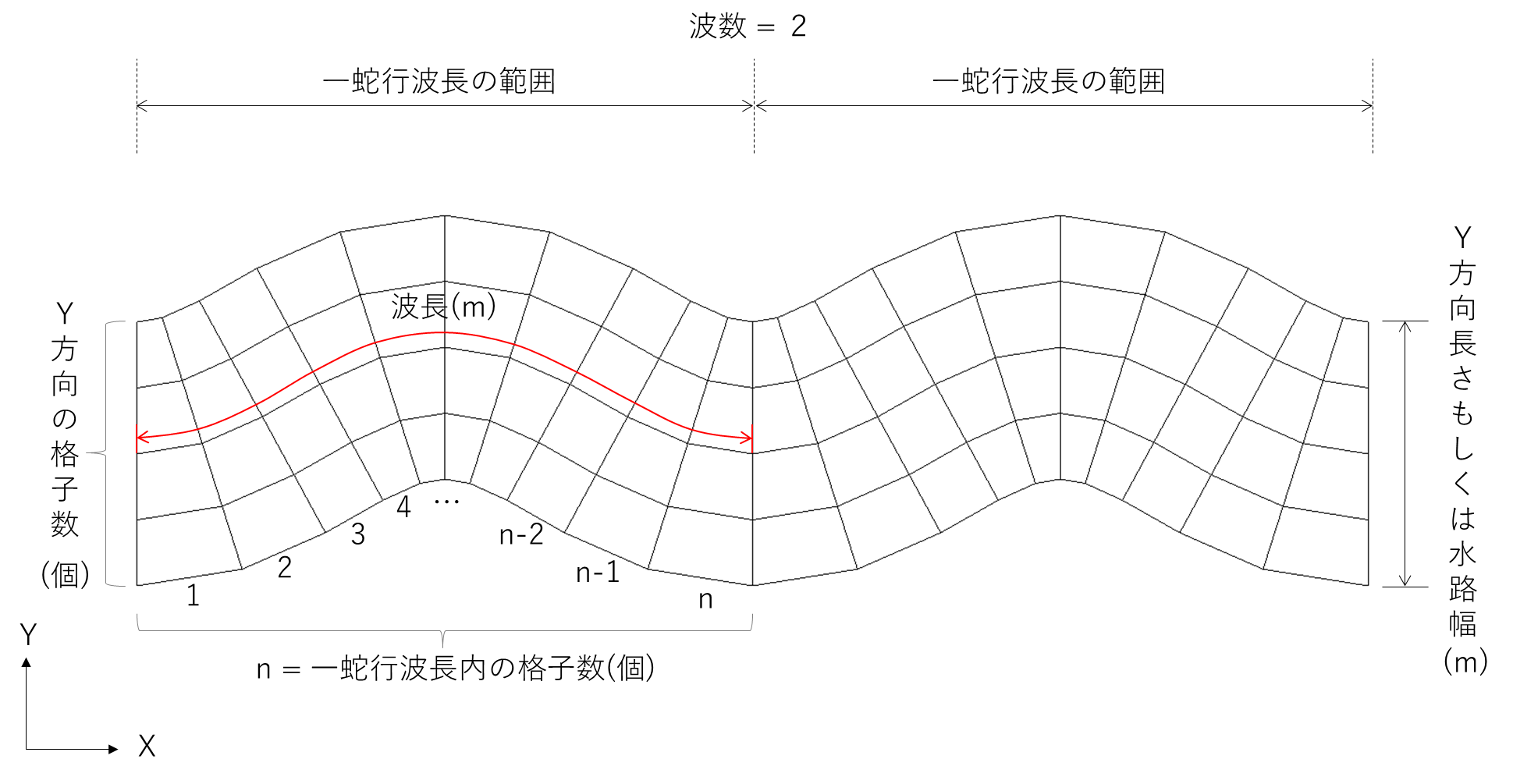
水路主要部の形状がサイン・ジェネレーテッド・カーブ蛇行水路の場合は共通項目の他に、水路の波長、一蛇行波長内の格子数、波数、蛇行角が必要となる。
各条件のイメージはこのようになる。
サインジェネレーテッド曲線については以下のページで解説が読めます。
こちらの記事を参考にして格子生成の流れを整理します。
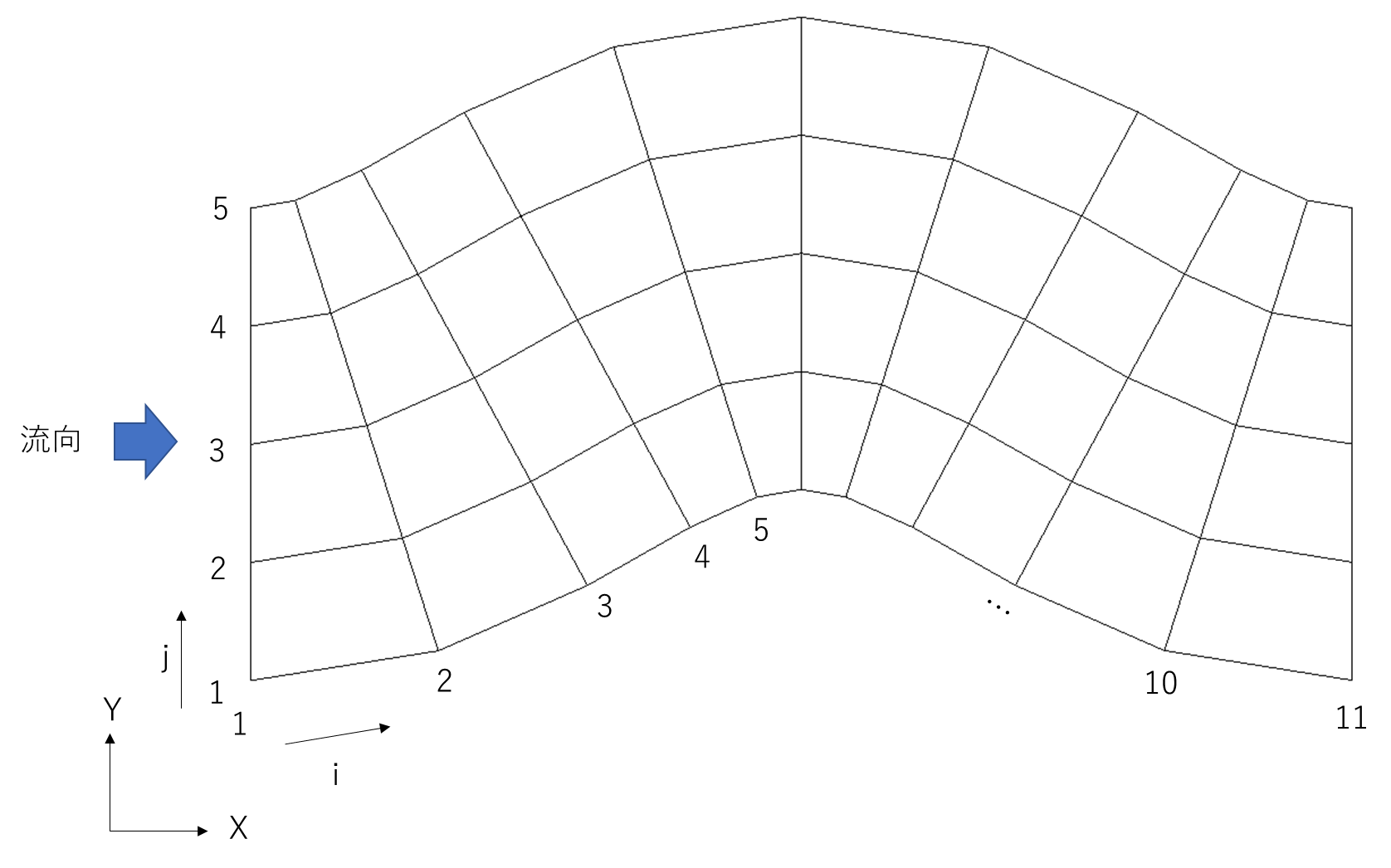
波長$L=$10m、一蛇行波長内の格子数$n=$10個、波数$N=$1波、蛇行角$\theta_0=$30°、水路幅$B=$4m、横断方向格子数$m=$4個の条件で作成した蛇行水路の格子を以下に示す。
この時、各格子点を上流端の右岸端からの流下方向の番号を$i$、右岸から左岸方向の番号を$j$として($i$,$j$)と表し、平面的な格子点の位置のプログラム上での計算方法を整理する。
格子作成の際にはまず、水路の中央線として入力した条件から一蛇行波長内の上流端から下流端にかけてサインジェネレーテッド曲線が計算される。
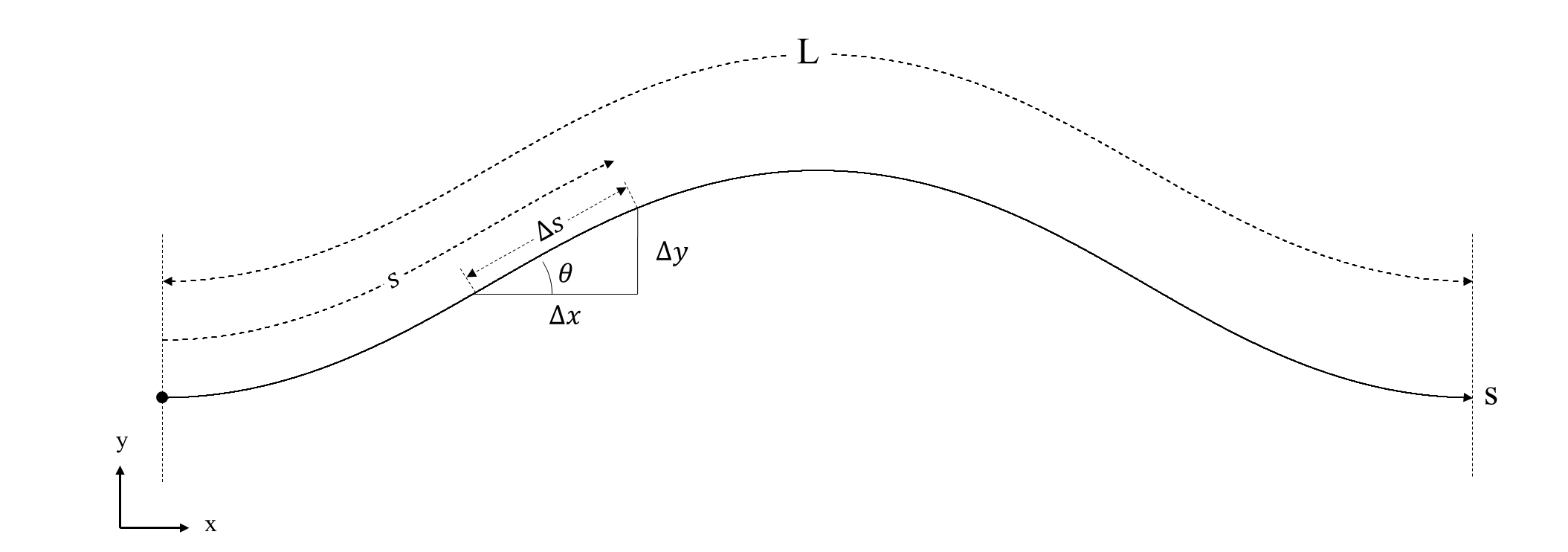
曲線の進行方向を$s$軸、蛇行角を$\theta_0$としたとき曲線の進行方向と水平方向の角度$\theta$は以下の式で表される。
\theta=\theta_0\sin(2\pi\frac{s}{L}) \tag{1}
この曲線を$x-y$座標に変換するには微小要素$\Delta s$を$s$軸に沿って逐次加算していき、その都度$\theta$を求め、$\Delta s$と$\theta$から$\Delta x$、$\Delta y$を求め、累加していきます。
微小要素$\Delta s$の$x,y$成分は以下の式で表せます。
\begin{align}
\Delta x=\Delta s \cos \theta\tag{2} \\
\Delta y=\Delta s \sin \theta\tag{3}
\end{align}
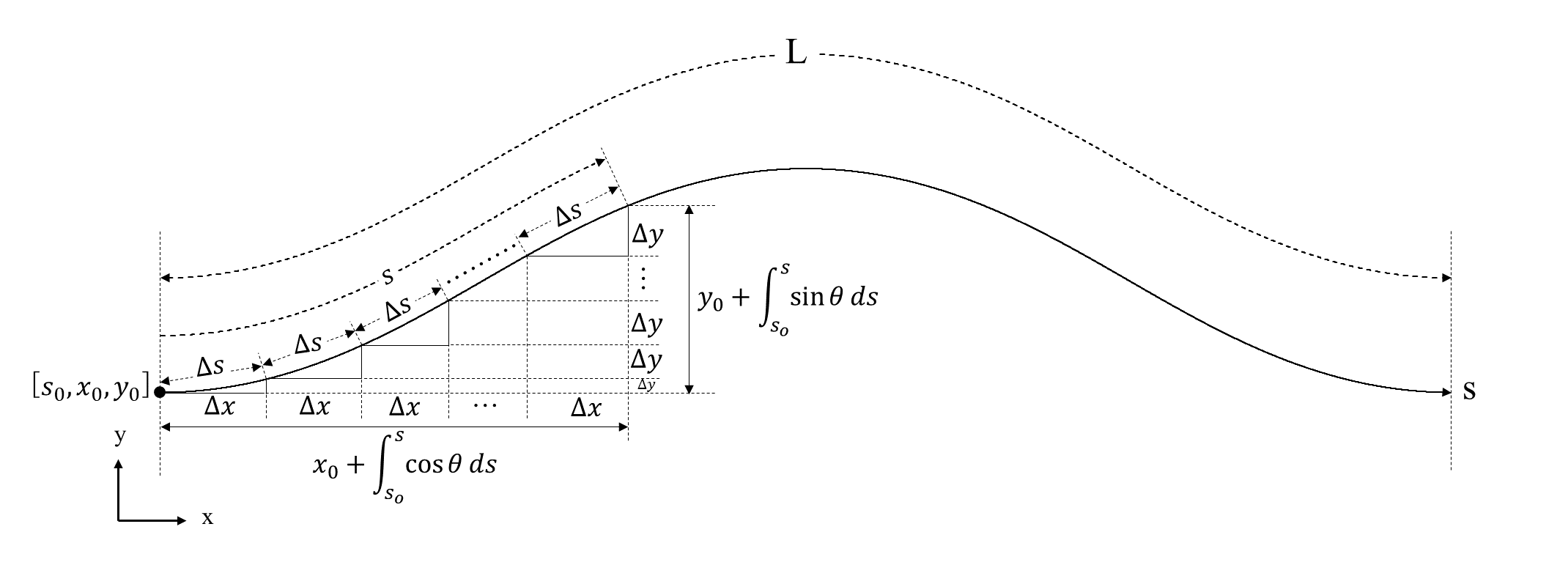
これらの式より、サインジェネレーテッド曲線の$s,x,y$は以下の式で表すことができました。
\begin{align}
s= s_0 + \int_{s_0}^{s}ds\tag{4}\\
x= x_0 + \int_{s_0}^{s}\cos\theta ds\tag{5}\\
y= y_0 + \int_{s_0}^{s}\sin\theta ds\tag{6}
\end{align}
ここで実際のプログラム上での動作を考えます。
本ツール上では$s$軸方向の微小要素$\Delta s$は波長$L$を$n$分割したものをさらに1000分割したものなので以下の式で表されます。
\Delta s=\frac{1}{1000}\frac{L}{n}\tag{7}
また、$s_0=0,x_0=0,y_0=0$であるため、式$(4)~(6)$はプログラム上では以下のような式で計算される。
\begin{align}
s= \sum_{k=1}^{1000n}\frac{1}{1000}\frac{L}{n}\tag{8}\\
x= \sum_{k=1}^{1000n}\frac{1}{1000}\frac{L}{n}\cos\theta\tag{9}\\
y= \sum_{k=1}^{1000n}\frac{1}{1000}\frac{L}{n}\sin\theta\tag{10}
\end{align}
ここで次に求めたいのは水路を縦断方向に$n$分割した時の断面$i$の水路中央の$x-y$座標だが、上流端から断面$i$までの$s$軸方向の微小区間数は$1000(i-1)$で表せるので断面$i$での値$s_i,\theta_i,x_{ci},y_{ci}$は以下のようにあらわせる。
\begin{align}
s_i= \frac{L}{n}(i-1)\tag{11}\\
\theta_i=\theta_0\sin(2\pi\frac{i-1}{n})\tag{12}\\
x_{ci}= \sum_{k=1}^{1000(i-1)}\frac{1}{1000}\frac{L}{n}\cos\theta\tag{13}\\
y_{ci}= \sum_{k=1}^{1000(i-1)}\frac{1}{1000}\frac{L}{n}\sin\theta\tag{14}
\end{align}
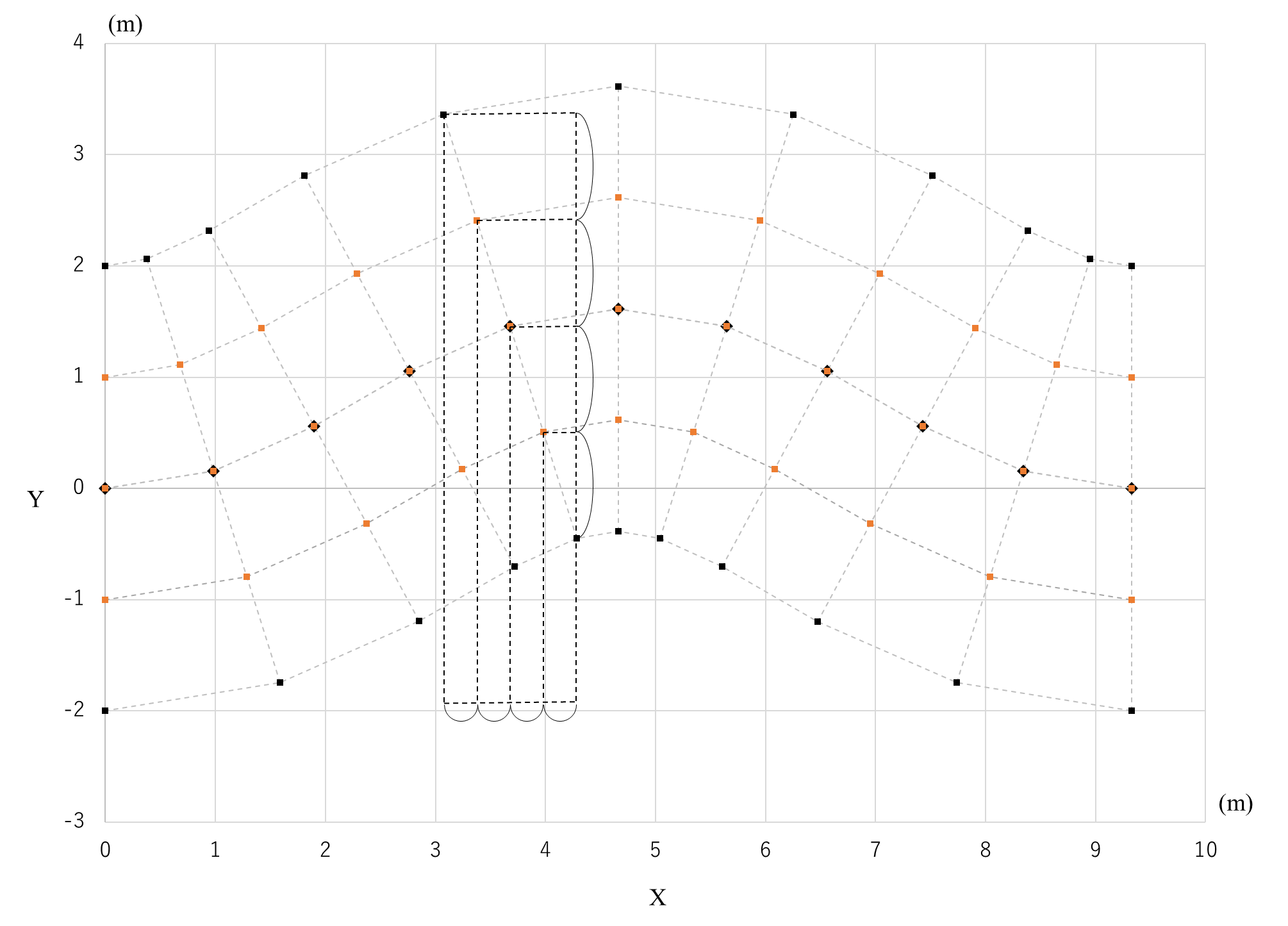
以下の図は上記の条件での水路中央線の座標を示したものである。
黒い線は各格子点間隔を1000分割し各分割点の座標をプロットしたものであり、上記の条件で作成したサインジェネレーテッド曲線を表している。橙色の◆が各格子点の座標を示し、橙の点線はそれらをつないだものである。
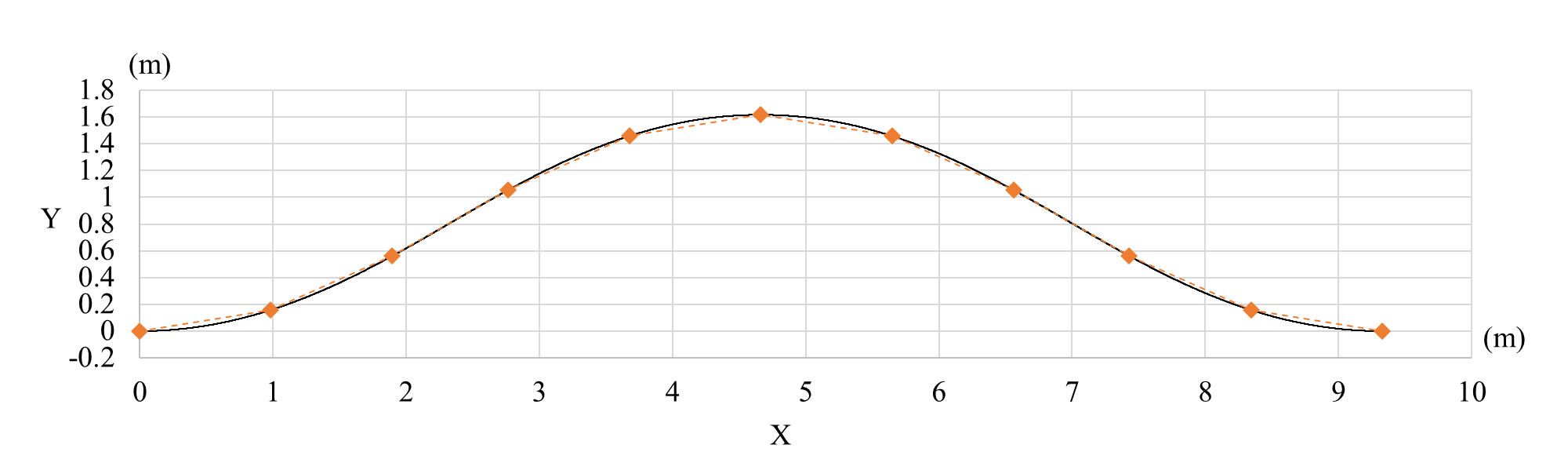
このようにして最初に水路中央の座標を求め、次に各断面で水路中央の座標から横断方向の格子点の座標が計算される。
各断面の横断方向の座標は、まずはじめに左右岸の一番端の座標を水路中央の座標と水路幅$B$と$y$軸方向に対する横断面の傾き$\theta$から求める。
断面$i$の右岸の座標[$x_{ri}$, $y_{ri}$]と左岸の座標[$x_{li}$, $y_{li}$]は以下の式で計算される。
\begin{align}
x_{ri}=x_{ci}+\frac{B}{2}\sin\theta\tag{15}\\
y_{ri}=y_{ci}-\frac{B}{2}\cos\theta\tag{16}\\
x_{li}=x_{ci}-\frac{B}{2}\sin\theta\tag{17}\\
y_{li}=y_{ci}+\frac{B}{2}\cos\theta\tag{18}
\end{align}
断面$i=5$での断面中央の座標と左右岸の座標の関係のイメージを以下に示す。
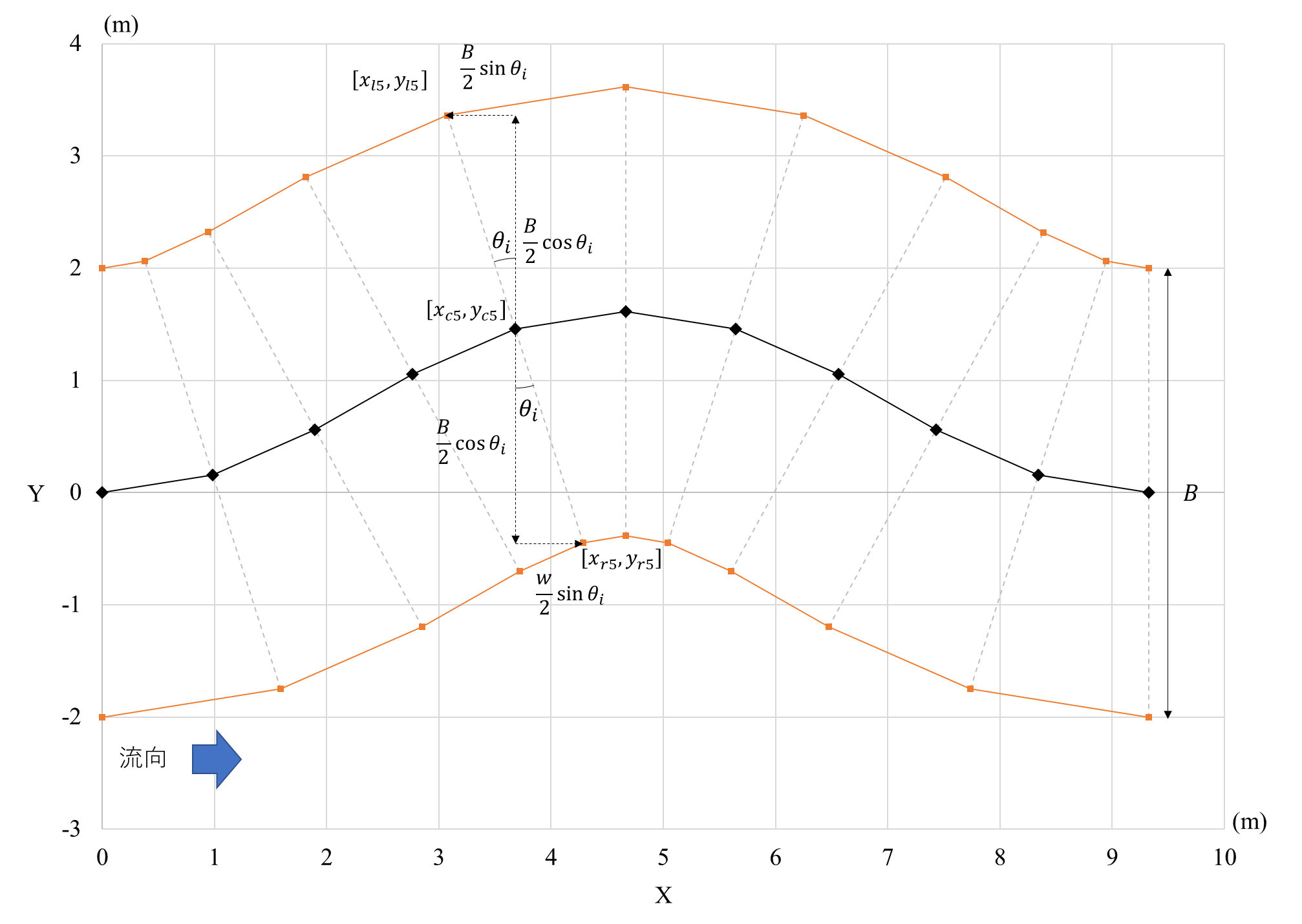
このように各断面の左右岸の座標が計算され、この2つの座標と横断方向の分割数から各断面横断方向の格子点の座標が計算される。
横断方向の分割数(格子数)を$m$とすると、格子点($i$, $j$)の座標は以下のようにして計算される。
\begin{align}
x_{ij}=x_{ri}+(x_{li}-x_{ri})\frac{j-1}{m}\tag{19}\\
y_{ij}=y_{ri}+(y_{li}-y_{ri})\frac{j-1}{m}\tag{20}
\end{align}
イメージとしては以下の図のようになる。
結局のところ各断面の左右岸をつないだ線分を横断方向格子数に分割するような位置が格子点の座標となる。
以上が入力した条件からサイン・ジェネレーテッド・カーブ蛇行水路の格子が生成される流れである。
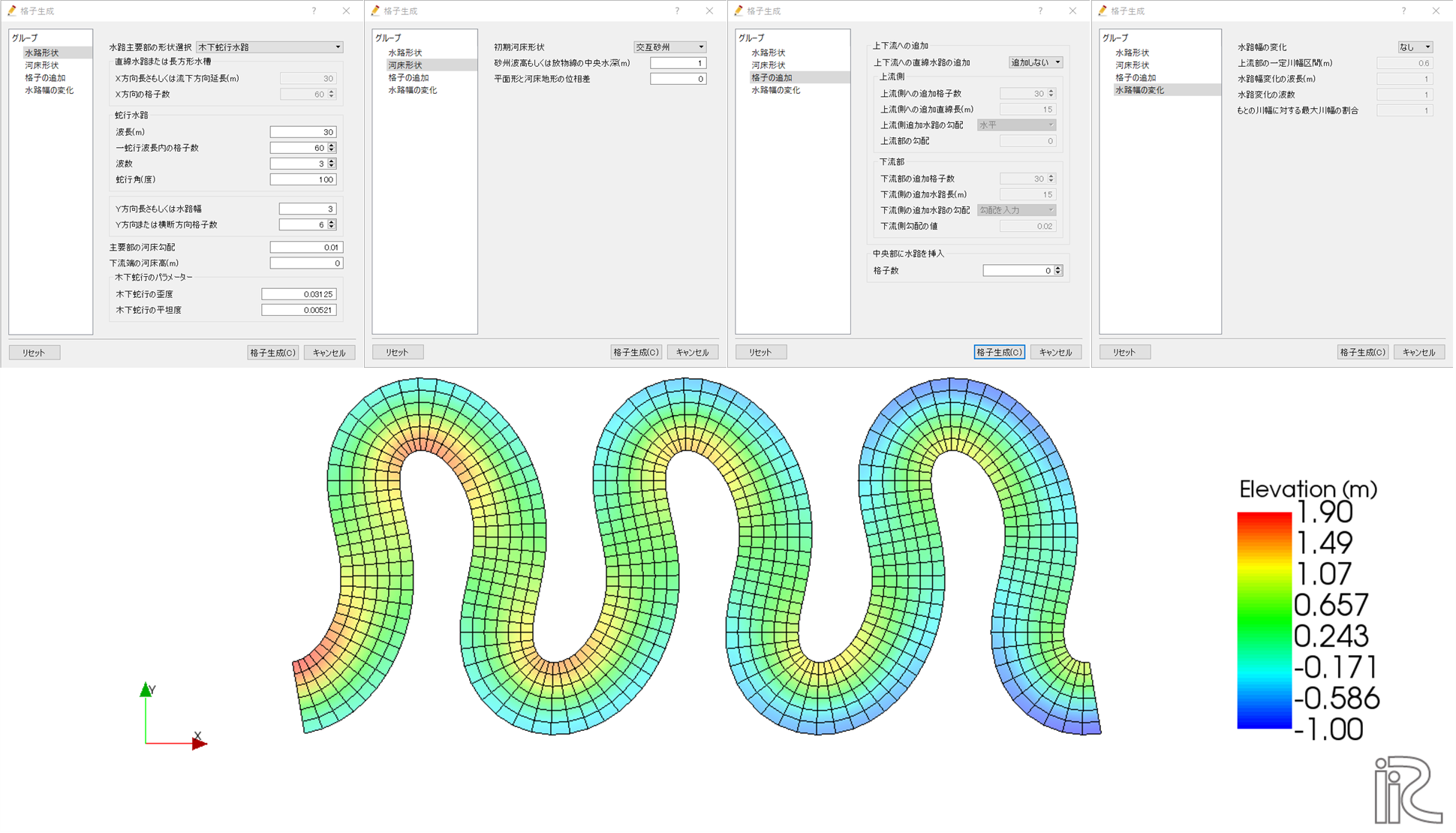
木下蛇行水路
木下蛇行水路では先ほどのサイン・ジェネレーテッド・カーブ蛇行水路に歪度と平坦度を設定することができる。
木下蛇行曲線についても以下を参考にした。
木下蛇行水路を選択した場合、格子作成の考え方はサイン・ジェネレーテッド・カーブ蛇行水路とほぼ変わらない。
ただし、蛇行曲線の進行方向と水平方向の角度$\theta$を表す式に歪度$J_s$と平坦度$J_f$が加わり以下のようになる。
\theta = \theta_0\sin\frac{2\pi s}{L}+\theta_0^3\Biggl(J_s\cos\biggl(3\frac{2\pi s}{L}\biggr)-J_f\sin\biggl(3\frac{2\pi s}{L}\biggr)\Biggr) \tag{21}
河床形状
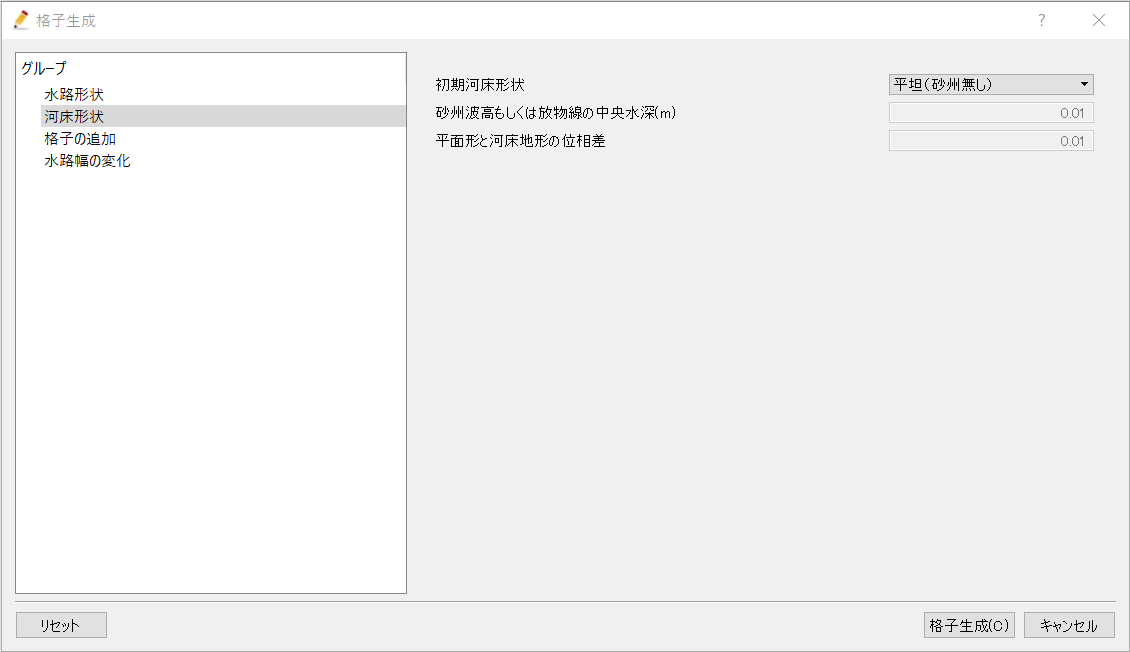
河床形状グループでは河床の形状の設定を行うことができる。
初期河床形状は平坦(砂州無し)、交互砂州、放物線から選択可能で断面形状のイメージとしては以下のようになる。
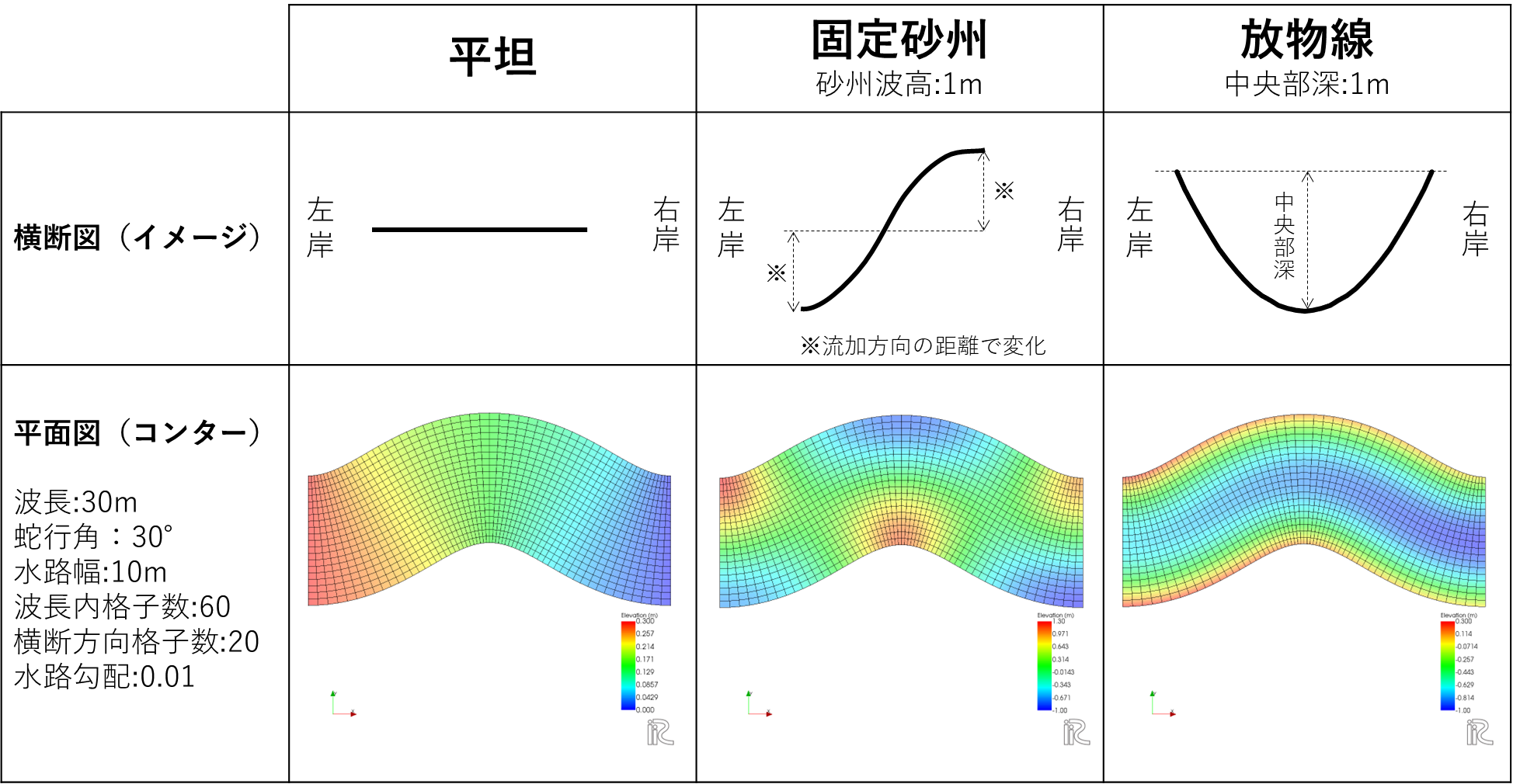
平坦(砂州無し)の場合は水路中央の地盤高が同じ断面内の格子点すべてに与えられる。
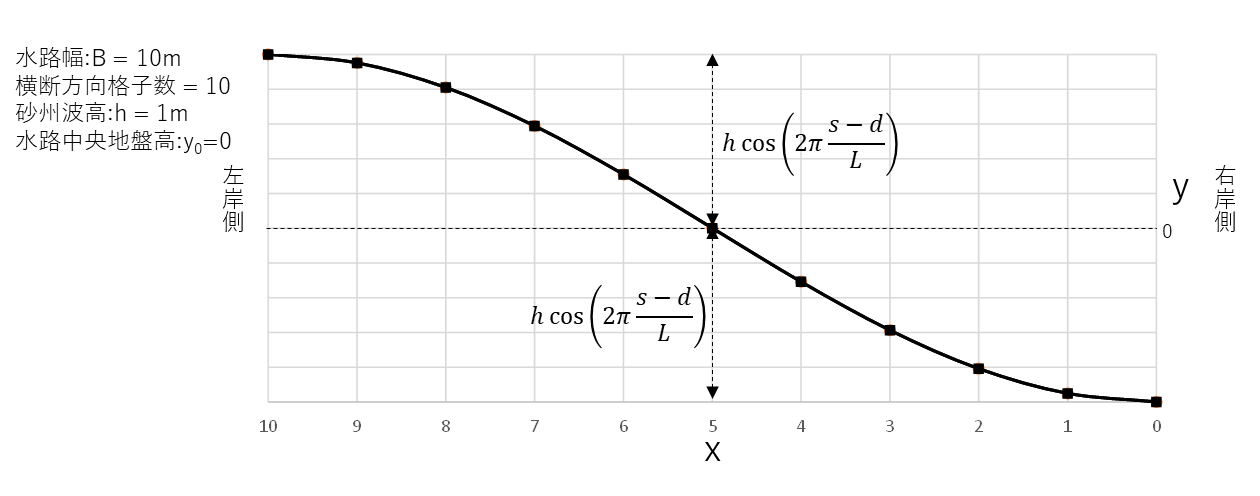
交互砂州の場合の断面$i$での地盤高$y$を考える。
上流端断面($i=1$)から断面$i$までの流下方向の距離を$s$、右岸端から左岸方向への距離を$x$、水路中央の地盤高を$y_0$、水路幅を$B$、砂州波高を$h$、平面形と河床地形の位相差を$d$、波長を$L$とすると$y$は以下の式で表すことができる。
y=y_0-h\cos\biggl(2\pi\frac{s-d}{L}\biggr)\cos\biggl(\pi\frac{x}{B}\biggr)
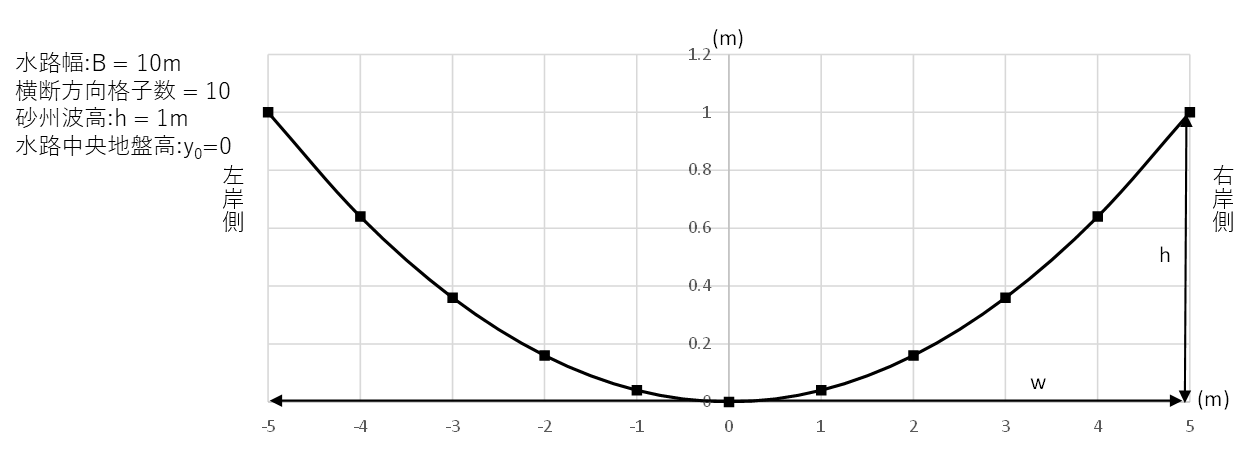
放物線の場合の断面$i$での地盤高$y$を考える。
水路中央からの距離を右岸側を正として$x$とし、水路中央の地盤高を$y_0$、水路幅を$B$、砂州波高を$h$とすると$y$は以下の式で表すことができる。
y=y_0+\frac{4h}{B^2}x^2
なお、水路中央の地盤高は水路形状グループで設定した、下流端の河床高をもとに下流端からの距離とメインの水路と追加した水路それぞれの勾配から求められる。
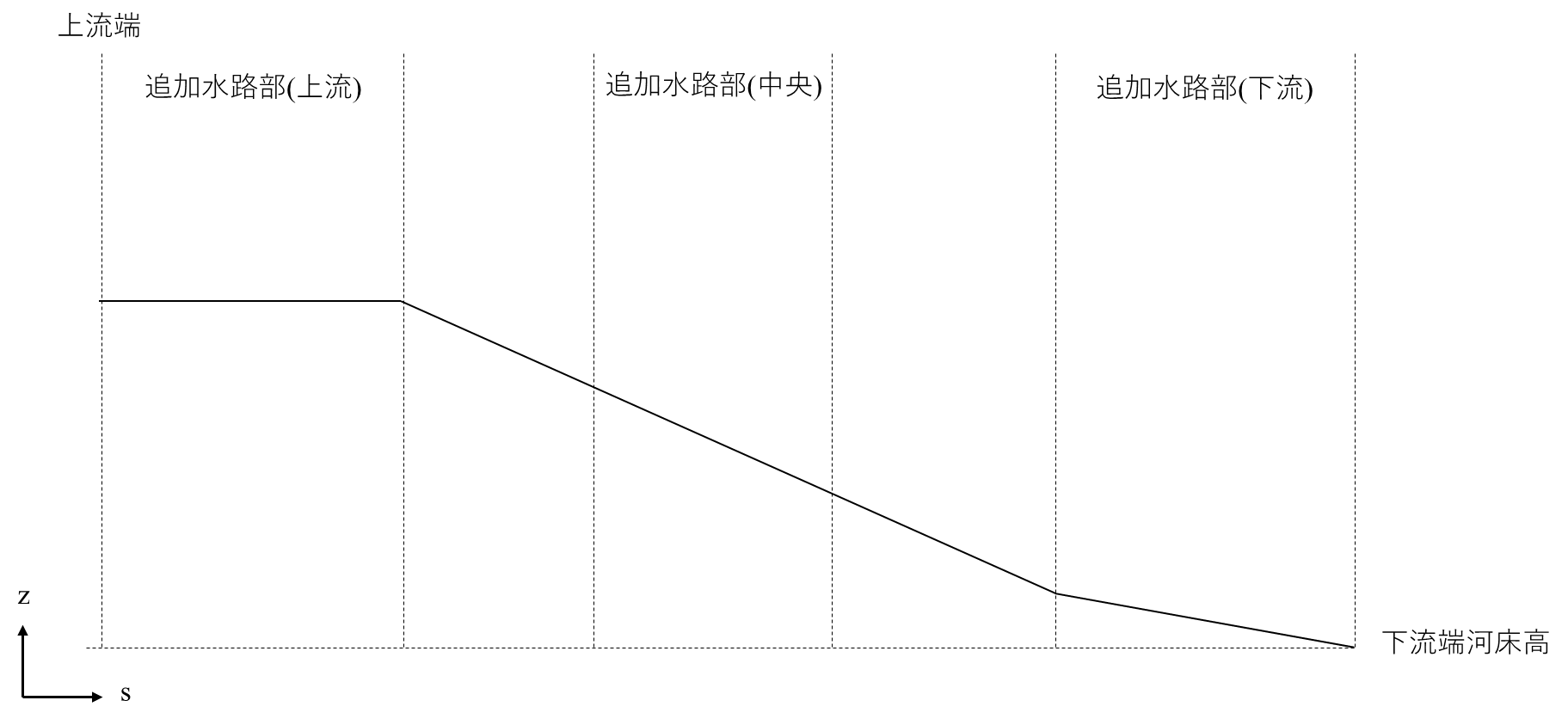
格子の追加
格子の追加グループで条件を入力すると水路形状グループで入力した条件で作成した格子の上流端、中央、下流端に直線の水路を追加することができる。
上下流端に直線水路を追加する場合には上下流への直線水路の追加で追加するを選択し追加格子数と追加直線長、勾配を上下流でそれぞれ入力する。なお勾配については水路形状グループで入力した勾配と同じ値を使用するか独自に勾配を設定するかを選択できる。
中央部に水路を追加する場合は格子数を設定する。
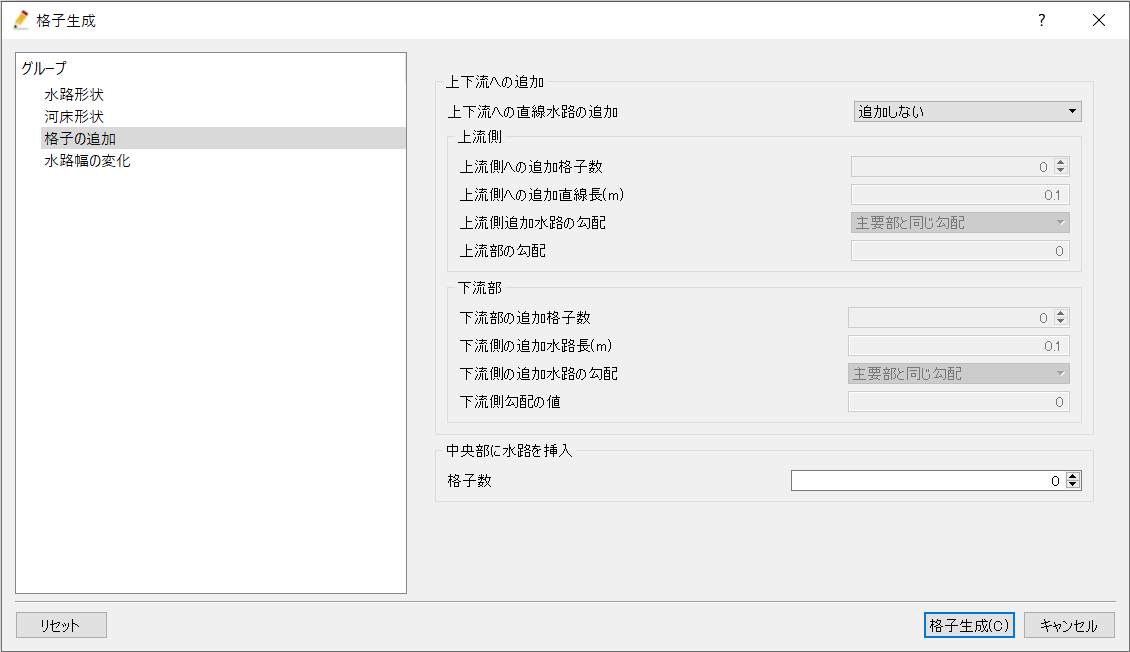
各種条件のイメージは以下のようになる。
水路中央に追加する直線水路のx軸方向の格子幅は水路形状グループの条件より作成した水路の流下方向中央の断面から上下流1断面までのx軸上の距離を半分にしたものとなる。
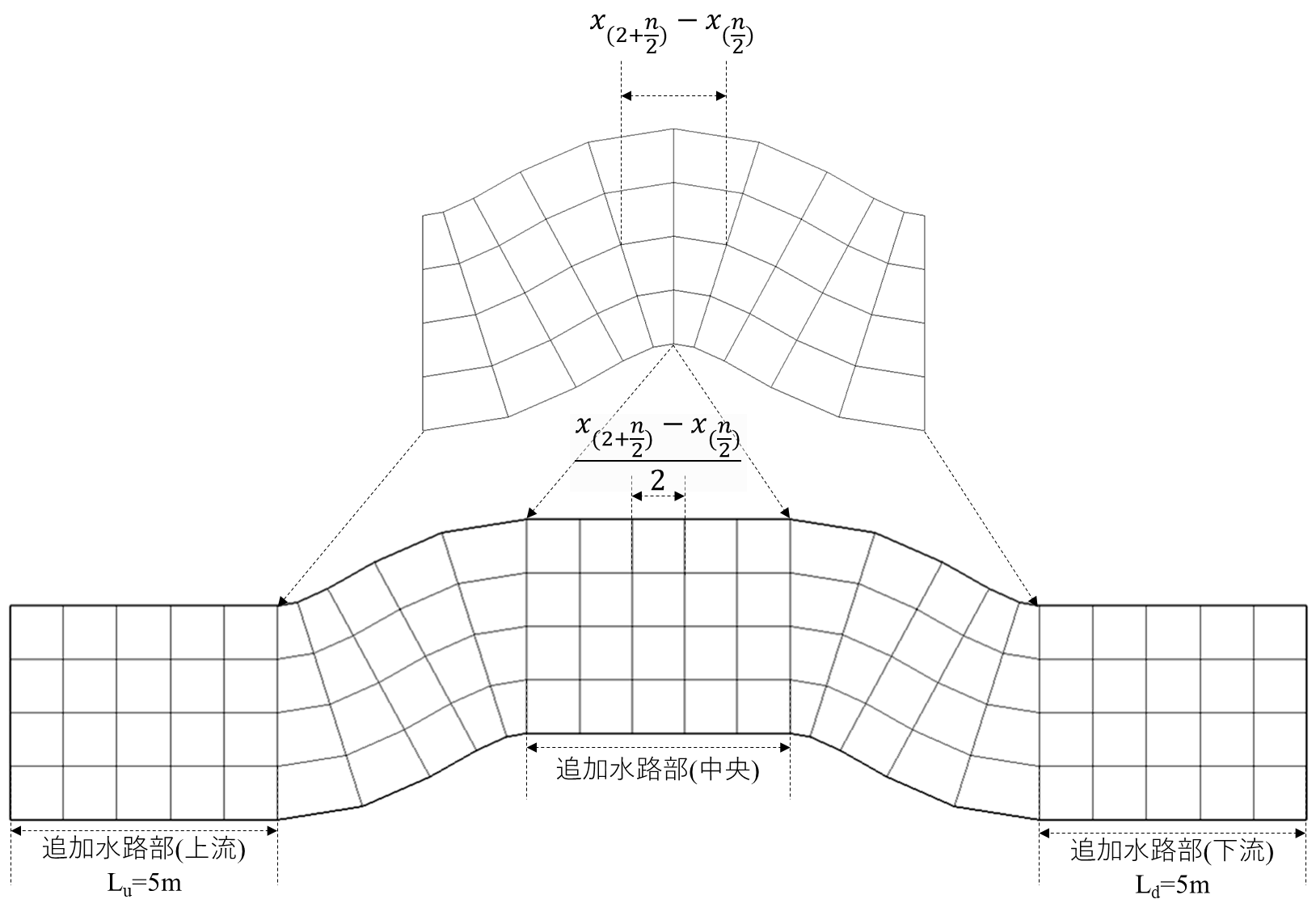
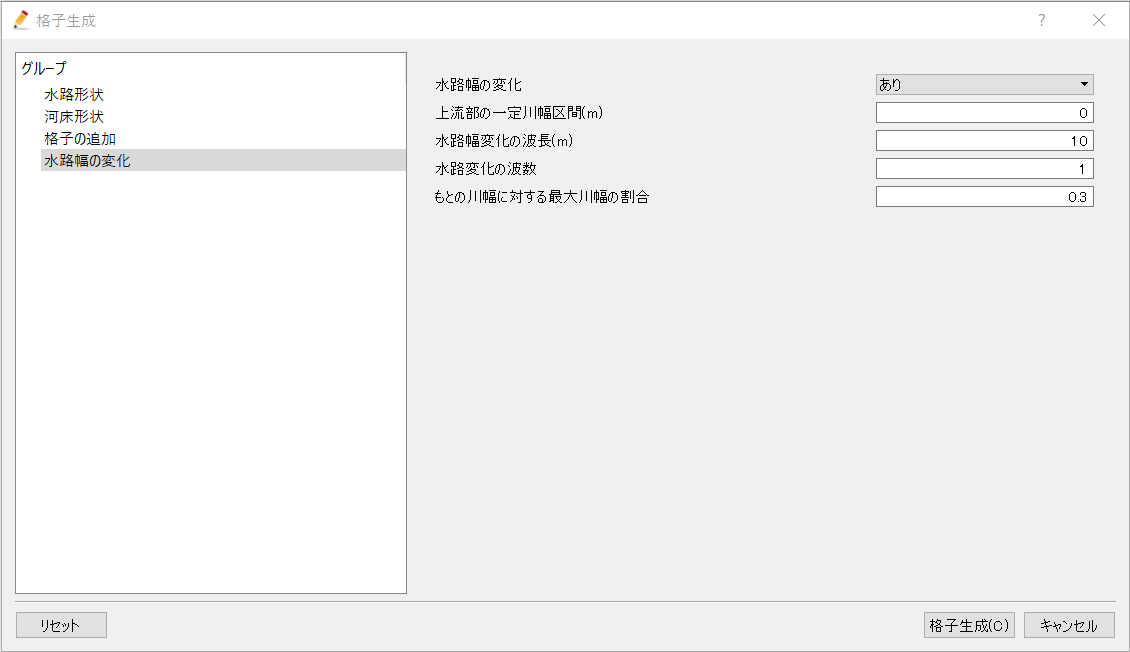
水路幅の変化
水路幅の変化グループでは水路の横断方向格子のサイズに変化を加えることが可能である。
この項目での入力条件から、水路形状グループと格子の追加グループの条件から作成された格子を変形させている。
このグループで水路幅の変化をありにすると変形が行われる。
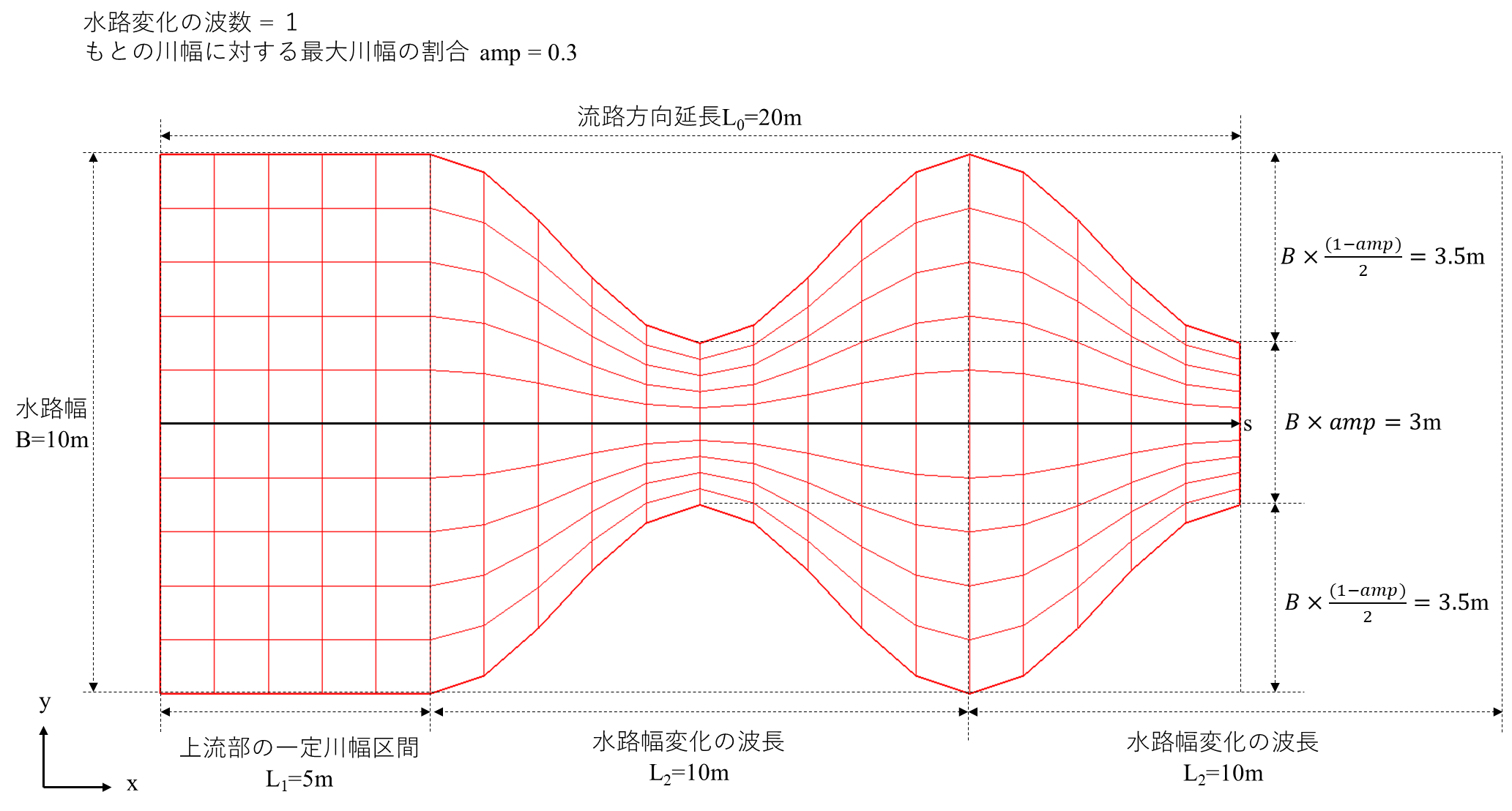
流下方向延長=20m、X方向の格子数=20、水路幅=10m、横断方向格子数=10の直線水路を、上流部の一定川幅区間=5、水路幅変化の波長=10m、水路変化の波数=1、元の川幅に対する最大川幅の割合=0.3の条件で水路幅を変化させた格子を例として以下に示す。
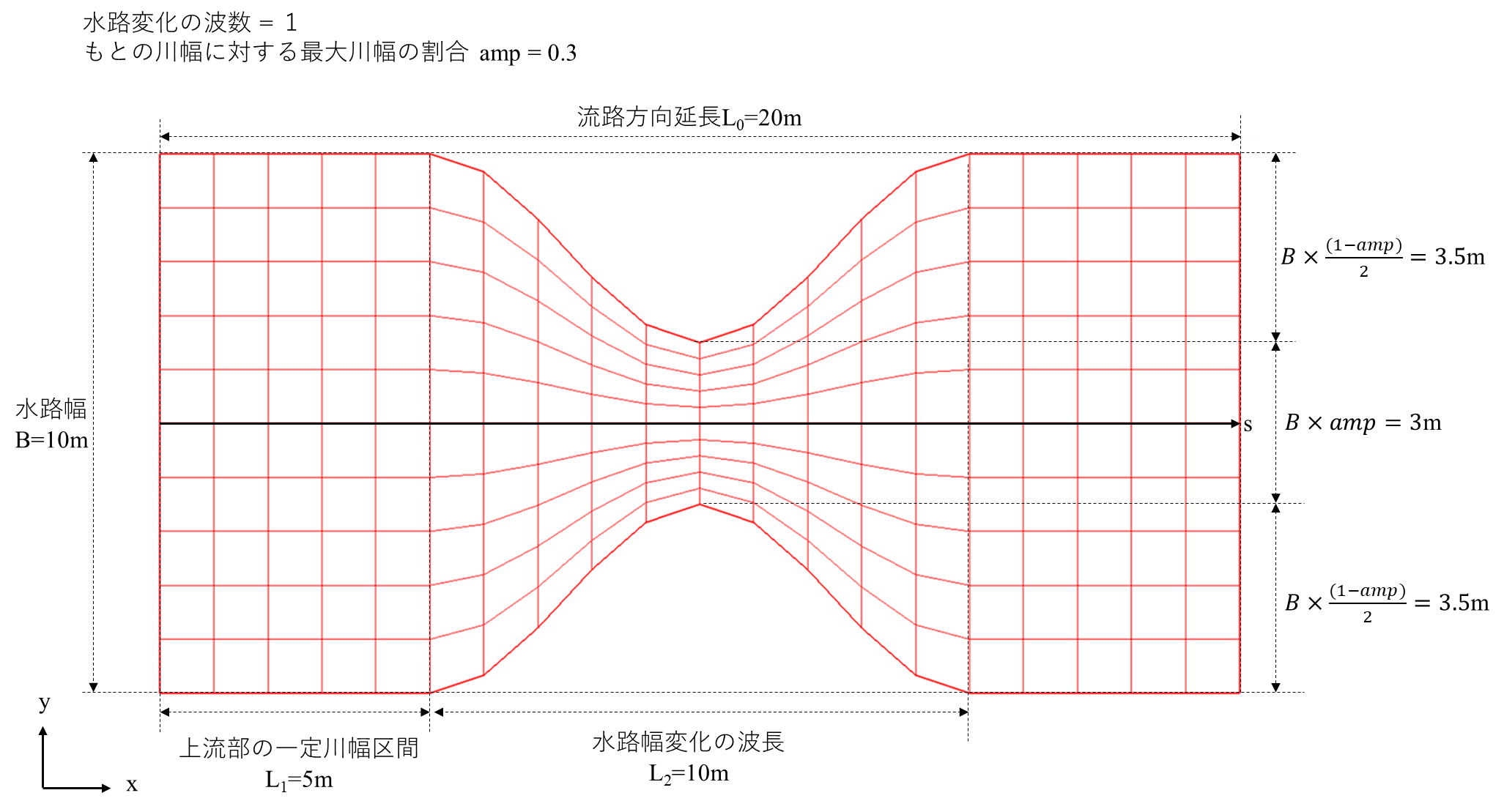
上記の図のように上流端から流下方向($s$軸方向)の延長$s$が$L_1\leqq s \leqq L_1+L_2$の区間で水路幅が変化する。
波数を増やした場合は以下のようになる。
上流からN個目の水路変化の波長内での格子点($i,j$)の座標[$x_{ij},y_{ij}$]の変化後の座標[$x_{ij}',y_{ij}'$]は以下の式で表すことができる。
h\_amp_i=\Biggl(\frac{amp-1}{2}(1-\cos\biggl(2\pi\frac{s_i-L_1-(N-1)L_2}{L_2}\biggr)+1\Biggr)\\
x_{ij}'=x_{ci}+(x_{ij}-x_{ci})h\_amp_i\\
y_{ij}'=y_{ci}+(y_{ij}-y_{ci})h\_amp_i
この式は断面$i$の水路幅が$s_i$によって変化する倍率$h\_amp$を乗じた値になることを示している。
格子生成条件まとめ
ここまでの格子生成条件について、実際に格子を生成する際には以下のような流れで作成される。
- 水路形状グループで入力した条件で直線水路、サイン・ジェネレーテッド・カーブ蛇行水路、木下蛇行水路のいずれかの格子が作成される。
- 格子の追加グループで入力した条件で1で作成された格子に追加の直線水路の格子が追加、挿入される。
- 水路幅の変化グループで入力した条件で2で作成された格子の横幅を変化させる。
- 水路形状グループ、格子の追加グループで入力した河床勾配と下流端の河床高(m)から各水路横断面中央部の河床高が計算される。
- 4で計算された各横断面中央河床高を基に河床形状グループで入力した条件で各断面の河床高が計算される。