「新しい相関係数」をわかった気になるためのコピュラ入門

「新しい相関係数」こと、Chatterjee correlationの紹介記事がXで話題を呼んでいると耳にしたので、流行に乗って補足の解説記事を書いてみます。

話題の記事

• 「新しい相関係数」について
• 新しい相関係数の理論的性質

関連論文

• A new coefficent of correlation
  • 当該相関係数は、2019年にChatterjee教授によって提案され, 論文は2021年に統計学四大誌の１つJASAに採録されました。
• A survey of recent developments in measures of association
  • 著者ご本人がChatterjee correlationとその周辺・拡張をまとめ直した論文です。
• The exact region and an inequality between Chatterjee's and Spearman's rank correlations
  • Chatterjee correlationとSpearmanのρの関係性を調べた最近の論文です。前者は後者より大幅に小さい値を取りがちで、その幅は最大で0.4だと主張されています。おもしろい。

「新しい相関係数」こと、Chatterjee correlationとは？

まず初めにデータは$X$の小さい順に並べ替えておきます。
データ${(X_i,Y_i)}_{i=1}^n$ がある時、XとYのChatterjee相関は以下のように計算されます。
ただし簡単のため、本記事では以下タイ（同じ値を取っているデータが複数存在する事）は存在しないものとします。

$$
\xi_n(X,Y) = 1 - \frac{3 \sum_{i=1}^{n-1} |r_{i+1} - r_i|}{n^2-1}
$$

ここで$r_i$は$Y_i$の順位（rank）を表します。

特徴

1. 順位のみから決まります。いわゆる順位相関係数というやつです。
   • 「スケーリングに影響されにくい」「外れ値にロバスト」等と巷で述べられているものの背景はこの点に集約されます。
   • スピアマンやケンドールもそうです。ピアソンは違います。
2. 非対称です。$\xi_n(X,Y) \neq \xi_n(Y,X)$
   • $(X,Y)$が同時に生じやすいという相関よりも, $X$で$Y$が説明できるかという回帰のイメージに近い
   • 上記の平均やmaxをとれば対称化することも一応可能。
3. 有限の$n$では$-\frac{1}{2}+O(\frac{1}{n})$ 〜 $\frac{n-2}{n+1}$の値を取る事が示されています。
4. i.i.d.仮定の下、データ数$n$が十分に大きい極限では以下の値 $\xi$ に収束します。こちらは定義から明らかに0から1の範囲の値を取ります。
   • 上限値は良いとして、下限値は$-\frac{1}{2}$ではないのかと気になるところですね。$\xi_n$が明らかな負の値を取ったときの解釈は「i.i.d.とはかけ離れてるデータだ」ということになると述べられています。[Chatterjee, JASA,2021]
     $$
     \xi(X,Y) = \frac{\int \mathrm{Var}(\mathbb{E}[1_{Y \geq t}\mid X]) d\mu(t)}{\int \mathrm{Var}(1_{Y \geq t}) d\mu(t)}
     $$

ここでいきなりコピュラを導入します

$\xi$の意味への理解を深めるため、ここでいきなりコピュラというものを導入したいと思います。

コピュラとは何か

今、XとYの相関を測ることを考えていますね。コピュラとは何かを簡単に述べると、"XとYの従属性に関する情報のみを残した"部分です。言い方を変えると、"XとYの（同時）分布から、相関構造に関係しない要素を排除した残り物"です。では、「相関構造に関係しない」とはどういう意味でしょうか？ここでは 「Xにしか依存しない要素」「Yにしか依存しない要素」は（片方の変数にしか左右されないのだから）相関じゃないよね 、という立場に立ちます。（★）

「（データの）相関を見たければ（その分布の）コピュラだけに注目すれば良い！」と言っても実は過言ではありません。

コピュラを得る手続き

お手元の二変数のデータ${(X_i,Y_i)}_{i=1}^n$ からコピュラを得る方法を天下り的に説明します。

1. まず $[0,1]^2$ という正方形領域を用意します。
2. そしたら、X側を、順位を変えないように均等に並べます。
3. その後、Y側を、順位を変えないように均等に並べます。これで完成です！

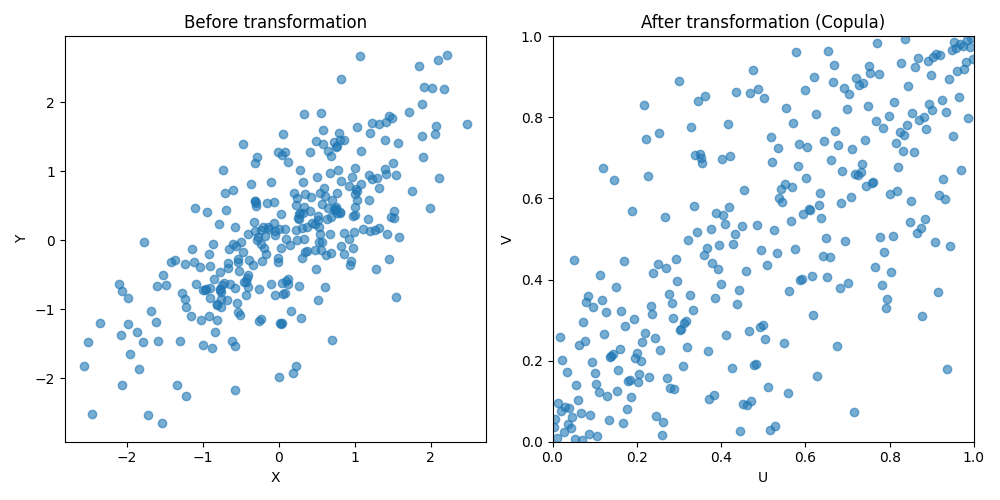
この操作の真意は「順位を保っている限りは相関構造は全く変化しないよね」「あらゆるデータを単位正方形上に移してやると統一的に議論（従属性の強さを測ったり）ができていいよね」の２点です。

右側の図を見ていただくと、コピュラ自身が $[0,1]^2$ 上の分布となっていることがわかります。この点も、数学的な扱いの上で都合が良いのです。

数式での理解

上記の変換は数式上は以下のように整理されます。（周辺分布が絶対連続の場合の説明です。）

$$f_{XY}(x,y) = f_X(x) f_Y(y) c(F_X(x), F_Y(y))$$

小文字が密度関数、大文字が累積分布関数です。
元の同時分布 $f_{XY}$ から周辺分布 $f_X / F_X$と$f_Y/F_Y$ が決まり、そこから右辺の$c$という関数形が決まるという流れが分かりやすいかと思います。この$c$が コピュラ（密度） と呼ばれています。¹

すなわち前節の順位を使って並べ替える操作でやりたかったのは、$x \to F_X(x)$, $y \to F_Y(y)$ という変数変換なのでした。²

$F_X$と$F_Y$はそれぞれ分布関数なので、$(x,y)$はちゃんと $[0,1]^2$上に移っていますね。そして右辺の$f_X$, $f_Y$はそれぞれのヤコビアンとして現れています。

前に述べた（★）の立場は、この定式化を使うと情報理論的な視点からも考えられます。
分布$f$のShannonエントロピーは $\int -f\log{f} d\mu$です。よって、$u=F_X(x), v=F_Y(y)$と置くと、以下の分解が成立します。
$$
-\int f_{XY} \log{f_{XY}} dxdy = -\int f_{X} \log{f_{X}} dx -\int f_{Y} \log{f_{Y}} dy -\int c \log{c}\ dudv
$$

すなわち$(X,Y)$が持つ"情報"から、右辺第１項「Xにしか依存しない要素」と右辺第２項「Yにしか依存しない要素」を除去した残り物である第３項が従属性に関する情報であり、それはコピュラ$c$にのみ依存しています。

Chatterjee correlationをコピュラで書き直します

いよいよ本題です。

1つめの表式

（$X$, $Y$の周辺分布が連続であるという仮定の下、）Chatterjee相関$(n\to\infty)$は以下のように書くこともできます。 [Ansari and Rockel, arXiv, 2025]

$$
\xi = 6\int_0^1 \int_0^1 \left( \frac{\partial C}{\partial t} (t,v)\right)^2 dtdv - 2
$$

順位相関係数はその名の通り順位を使って計算するのですが、その意味を少し考えると、コピュラのみから決まることもわかると思います。
特徴1で述べたようにChatterjee相関は順位相関係数の１つなので案の定コピュラ$C$のみから決まっていることが見て取れると思います。頭の６倍や最後の-2は[0,1]に収めるための調整項です。

その中でも特にChatterjee相関はコピュラ（分布関数）$C(u,v)$ の$u$での偏微分 $\frac{\partial C}{\partial u}$を測っているようですね。この値は理解しづらいですが、元の確率変数で言えば、$X$を既知としたときの$Y$の条件付き分布に相当します。

さてここからさらに直感的なイメージがつきやすい形に変形していきましょう。

2つ目の表式

この表式への変形は容易ですね。
$$
\xi = 6\int_0^1 \int_0^1 \left( \frac{\partial C}{\partial t} (t,v) ^2- v^2 \right) dtdv
$$

$X$と$Y$が独立な時、コピュラは$C(u,v)=uv$なので、$\frac{\partial C}{\partial u} (t,v) = v$となります。そのためこの表式にすると、$\frac{\partial C}{\partial t} (t,v)$と $v$ の乖離を測っている、すなわち独立の場合とどれ程離れているかを計算していることが見えやすくなりました。

このように$\frac{\partial C}{\partial u}$と$v$の乖離を測っていることが分かると、素朴な疑問が湧きます。何故それぞれの２乗を取った差分を計算しているのでしょうか？代わりに違う差分を使えば新たな相関指標が構築できるかもしれません！例えば愚直な差分
$\int_0^1 \int_0^1 \left( \frac{\partial C}{\partial t} (t,v) - v \right) dtdv$ としてみると、これは常に0になってしまいNGです。一方で差の絶対値を取り、$\int_0^1 \int_0^1 \left| \frac{\partial C}{\partial t} (t,v) - v \right| dtdv$ としてみるどうでしょうか？この要領でChatterjee相関の亜種が作れるかもしれません。 ³

３つ目の表式

最後に密度関数での表示を検討します。

$$
\xi = 6\int_0^1 \int_0^1 \left( \int_0^v c(t,s_1)ds_1\right) \left( \int_0^v c(t,s_2)ds_2\right) dtdv -2
$$

$$
= 6 \int_0^1 \int_0^1 \int_0^1 (1-\max{(s_1,s_2)}) c(t,s_1) c(t,s_2) dt ds_1 ds_2 - 2
$$

$$
=6({E_p[1-\max{(s_1,s_2)}] - E_{u}[1-\max{(s_1,s_2)}]})
$$

つまり$U=t$で"縦"に切られたコピュラ密度関数から、$s_1$と$s_2$という２つのサンプルを取ってみて、$1-\max{(s_1,s_2)}$が取る値の期待値を計算しています。この$1-\max{(s_1,s_2)}$の直感的意味は、

「同じ条件 $U=t$ のもとで2回引くと、どれだけ一緒に下側に寄るか」

です。$\xi$の表式に戻ると、

• 第１項が同じ$U=t$を共有するときに同じ条件付き分布から$s_1, s_2$を引いた場合（その同時密度は$p(s_1,s_2) = \int_0^1 c(t,s_1)c(t,s_2) dt$）
• 第２項は、$p$がもしも仮に一様だった場合（そのとき同時密度は一様$u(s_1,s_2) = 1$）

に相当しますので、やはり従属性が全くなかった場合との乖離を測る形になっています。

まとめ

• $(X,Y)$の相関（含む従属構造）を正方形領域$[0,1]^2$上の$(U,V)$に変換して、コピュラを通して見る方法を紹介しました。
• 話題のChatterjee相関の異なる表式をコピュラを通して３種類紹介しました。
  • コピュラの第一変数による一階偏微分（もしくはコピュラ密度の第二変数に関する積分）が鍵を握っており、この点が従来の$XY$間の対称性を有する順位相関（スピアマンやケンドール等）と決定的に違いました。
• Chatterjee相関の意味合いを数式を一切使わずに述べると、強いて言えば

「同じ$X/U$の値をとったという条件のもとで２回$Y/V$を引くと、それらがどれだけ一緒に下側/0側に寄るか」というある種の連動度が、仮に完全に独立（無相関）だった場合と比べて相対的にどれ程大きいのか？」を期待値の意味で測っている

となるでしょうか。

おわりに

• 分量としては少なめになりますが、Chatterjee correlationの直感的理解の一助になれば幸いです。
• 内容に誤り等ありましたらコメントにてご指摘ください。

参考文献

Sourav Chatterjee. A new coefficient of correlation. J. Am. Stat. Assoc., 116(536):2009–2022, 2021.

Sourav Chatterjee. A survey of some recent developments in measures of association. InProbability and Stochastic Processes. A volume in honour of Rajeeva L. Karandikar, pages
109–128. Singpore: Springer, 2024.

Jonathan Ansari, Marcus Rockel. The exact region and an inequality between Chatterjee’s and Spearman’s rank correlations. arXiv e-print., 2025.

また追加で、コピュラ統計学に興味を持った方向けにおすすめの文献を貼っておきます。

• Introduction to copulas (Nelsen, 2007)
  • 不動の教科書
• Everything You Always Wanted to Know about Copula Modeling but Were Afraid to Ask (Genest and Favre, 2007)
  • 読みやすいです
• コピュラの金融実務での活用 (吉羽要直, 2009)
  • 金融実務でのコピュラの活躍を垣間見れるスライドです。

1. 本当は定義の順番が違い、累積分布関数側から定義されます。本稿の説明はかなり天下り的ですが、ご了承ください。本来は、$[0,1]^2$上の関数$C$の端点での値と2-increasingという性質から定義がなされます。 ↩

2. ただ分布関数を使った変数変換なのですが、「確率積分変換」という格好いい名称がついています。 ↩

3. 私が調べた限りではこのような定義のものは見当たりませんでした。が、いかにもありそうな形です。 ↩