東京大学・株式会社Nospareの菅澤です.
前回の外れ値とロバスト推定(1)に引き続き,今回は線形回帰モデルにおける外れ値とロバスト推定について解説していきます.
外れ値と高レバレッジ点
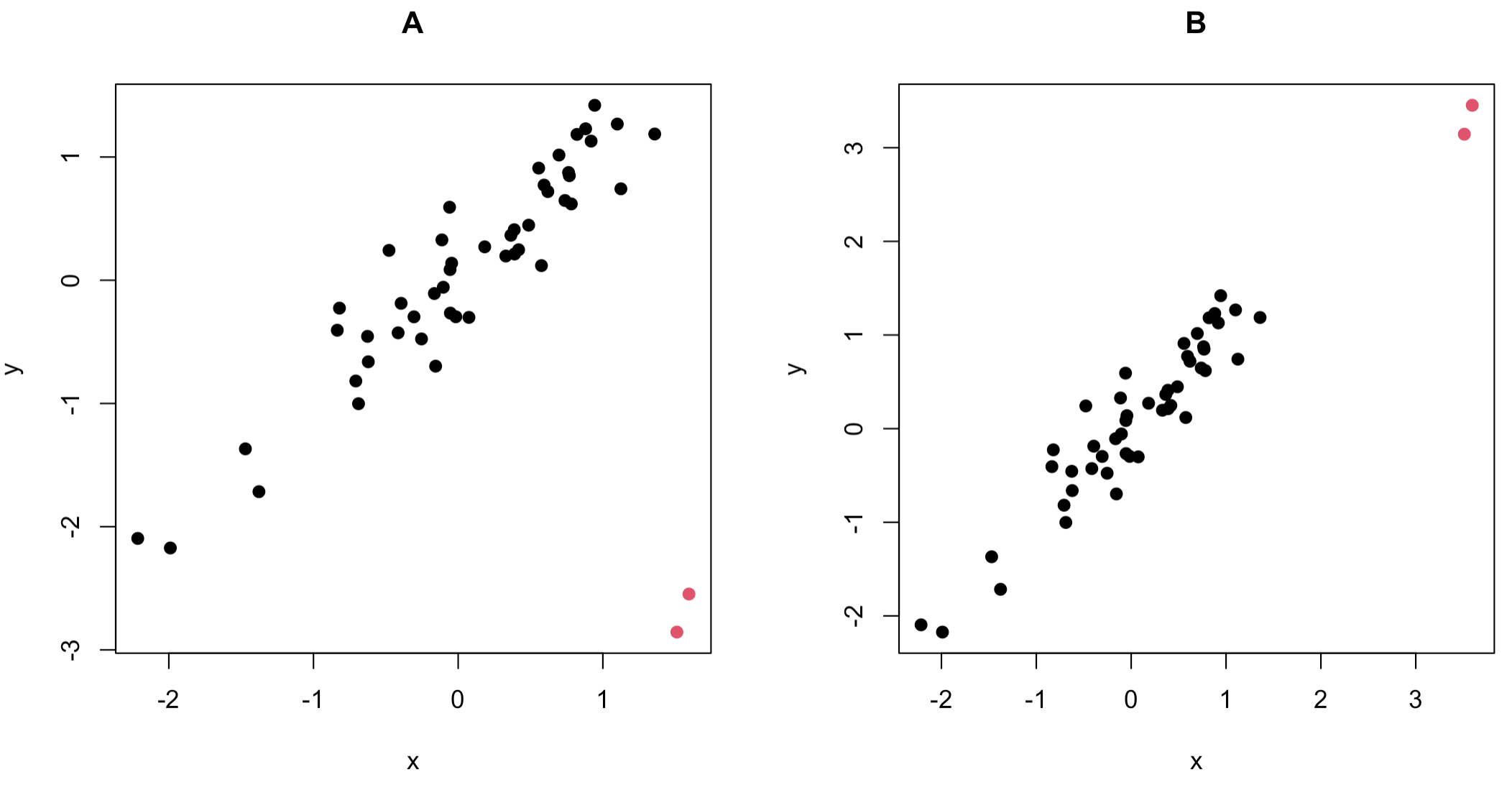
簡単な単回帰モデルの例を考えます.まずは以下の2つの散布図を見てみましょう.
どちらのケースでも,黒色で示されているデータ点の集合から離れた赤い点のデータの存在が確認できます.どちらの場合も2次元のデータとして捉えた際には赤い点は外れ値となります.ただし,$y$を$x$で説明する回帰モデルに興味がある場合は,赤い点が与える影響は異なってきます.
両ケースにおいて,単回帰モデル
y_i=\beta_0+\beta_1x_i + \varepsilon_i, \ \ \ i=1,\ldots,n
を考えます.ここで$E[\varepsilon_i]=0$かつ${\rm Var}(\varepsilon_i)=\sigma^2$です.
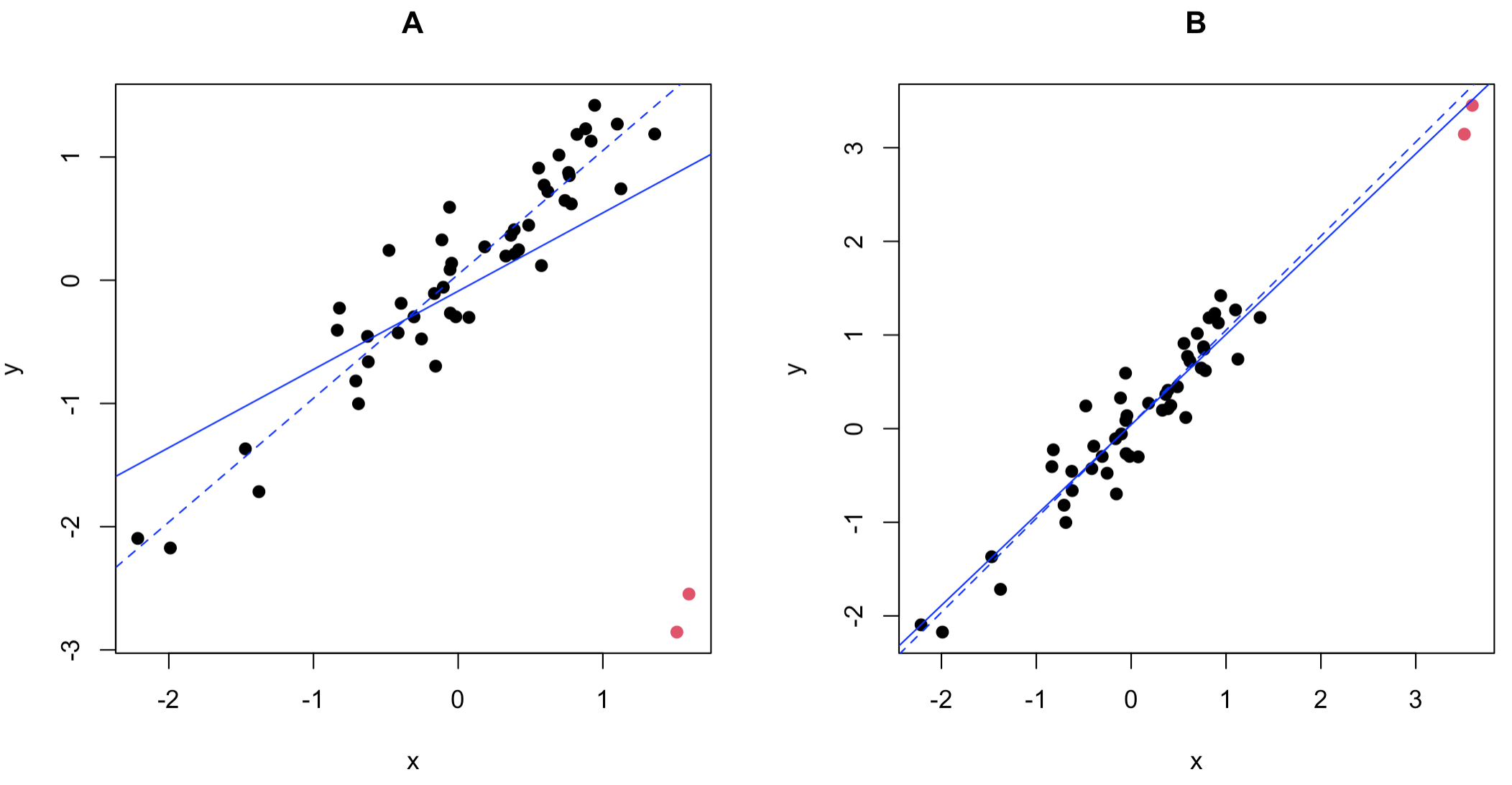
全てのデータ点で推定した回帰直線(青実線)と赤い点以外のデータ点で推定した回帰直線(青点線)を以下に示します.
この図からケースAでは赤い点の有無によって回帰直線が大きく変化するのに対して,ケースBでは回帰直線がほとんど変化しないことがわかります.両者の違いは赤い点と回帰直線の距離です.ケースBの赤い点は回帰直線に近い場所に位置しているのに対して,ケースAの赤い点は回帰直線から大きく離れた場所に位置していることが観察できます.
このように,多次元データとして外れ値だったとしても,回帰分析のように$y$と$x$の関係性について興味がある場合は,推定結果に影響を与えるケースと与えないケースがあります.回帰分析において外れ値といった場合は一般的にケースAのような状況を指します.
ちなみに,ケースBの赤い点のようなデータ点は**高レバレッジ点(high leverage point)**と呼ばれます.これは説明変数の外れ値として解釈することができます.
今回のような単回帰(説明変数が1つ)の場合は,視覚的に外れ値を見つけることが可能ですが,説明変数の数が増えるとデータを可視化することが困難になります.その場合,残差を調べる(残差分析を行う)ことで外れ値の存在について考察することが可能です.
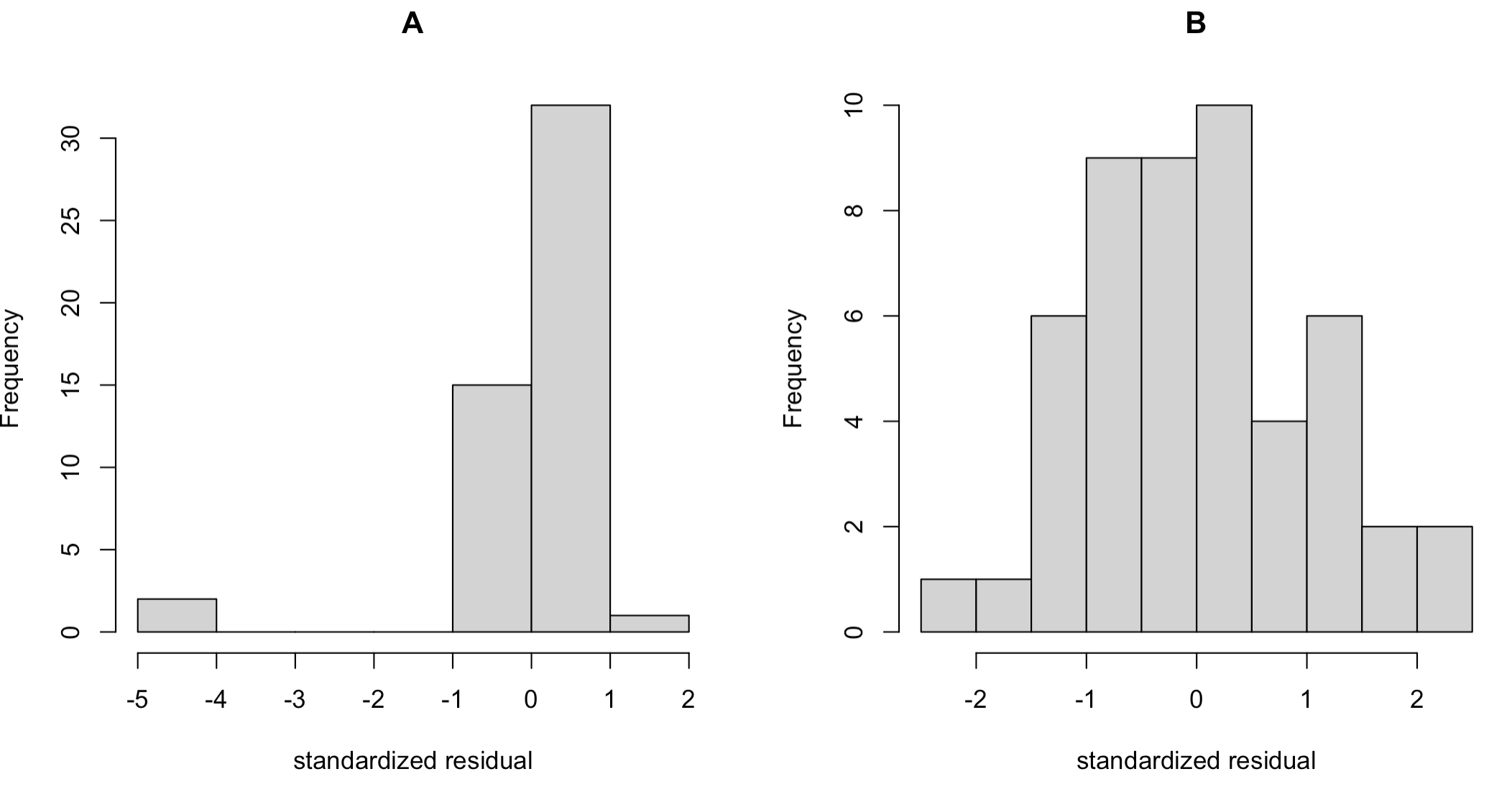
具体的に,標準化残差$\hat{\sigma}^{-1}(y_i-\hat{\beta}_0-\hat{\beta}_1x_i)$を計算し,そのヒストグラムを描くと以下のようになりました.
ケースAでは著しく小さい残差の値をもつデータ点があることがわかります.これが図中の赤点に対応する残差です.このように,残差を調べることで外れ値をわかりやすく可視化することができ,場合によっては外れ値を除去して再度回帰モデルを推定することもできます.また,残差は説明変数の数に関係なく一次元の量なので,重回帰でも同様の方法が使えるのもポイントです.
線形回帰モデルのロバスト推定
残差を可視化することで外れ値の存在をチェックすることができますが,「回帰直線を推定して外れ値を検出し(除外し)再び回帰直線を当てはめる」といったトライアンドエラーの方法では手間がかかります.したがって,外れ値の影響をコントロールしつつ回帰モデルを推定する(外れ値処理と回帰モデルの推定を同時に実行する)ことが可能なロバストな推定手法が有効になってきます.
以下のような一般的な線形回帰モデルを考えます.
y_i=x_i^\top \beta +\varepsilon_i, \ \ \ \ i=1,\dots,n
ここで$x_i$は説明変数のベクトル,$\beta$は回帰係数のベクトルで,$\varepsilon_i$は$E[\varepsilon_i]=0$かつ${\rm Var}(\varepsilon_i)=\sigma^2$を満たす誤差項とします.
最小二乗法(OLS; ordinary least squares)による$\beta$の推定量は
\sum_{i=1}^n (y_i-x_i^\top\beta)^2
を最小化することで与えられますが,外れ値に対しては$(y_i-x_i^\top\beta)^2$の値が大きくなってしまい,その値に推定値が引っ張られてしまいます.
このような性質を改善した推定手法としてHuberの方法とTukeyの方法を紹介します.
どちらの手法も以下のような形の損失関数を考えます.
\sum_{i=1}^n \psi\left(\frac{y_i-x_i^\top\beta}{\sigma}\right)
ここで$\psi(\cdot)$は損失関数の形状を決める関数で,最小二乗推定量は$\psi(x)=x^2$のケースに相当します.
$\psi(\cdot)$の引数には標準化残差が入っているのがポイントです.標準化残差が大きい場合 (データが外れ値である場合) に,$\psi(\cdot)$の値があまり大きくならないような$\psi(\cdot)$の関数形を選ぶことによってロバストな推定を実行するというのが基本的なアイデアです.
そのため,以下で紹介する方法を実行するには$\sigma$の推定も必要となります.その方法はいくつか考案されていますが,今回はあくまで適切な$\sigma$の値が推定できたもとで$\beta$をどのように推定するかに焦点を当てます.
Huberの方法
$\psi(\cdot)$として以下のような関数を考えます.
\psi_K(x)=\begin{cases}
x^2 & (|x|<K) \\
2K|x|-K^2 & (|x|\geq K)
\end{cases}
この関数は標準化残差の絶対値が小さい領域では最小二乗法と同様に$\psi(x)$は二次関数になっていますが,標準化残差が大きい領域では一次関数に変化しています.これにより,標準化残差$\sigma^{-1}(y_i-x_i^\top\beta)$が大きい外れ値に対して$\psi_K(\sigma^{-1}(y_i-x_i^\top\beta))$の値が大きくなりすぎず,外れ値が$\beta$の推定に与える影響を抑えることができます.
上の定義において$K$はロバストな度合いを調整するチューニングパラメータになっており,小さい$K$ほど推定結果がロバストになります.$K=1.345$が標準的な値としてよく使われています.
また,$K\to\infty$で$\psi_K(x)$は最小二乗法に対応する$\psi(x)=x^2$に一致します.
通常の最小二乗法と異なり,Huber型の関数$\psi_K$を用いた損失関数の最小解は解析的に得られません.そこで,**繰り返し重み付き最小二乗法(IRLS; iteratively re-weighted least squares)**と呼ばれる方法で推定します.
損失関数を$\beta$について微分すると以下のような推定方程式が得られます.
\sum_{i=1}^n w_i(y_i-x_i^\top \beta)x_i=0, \ \ \
w_i=\begin{cases}
1 & (\sigma^{-1}|y_i-x_i^\top \beta|<K) \\
\sigma K/|y_i-x_i^\top \beta| & (\sigma^{-1}|y_i-x_i^\top \beta|\geq K)
\end{cases}
この方程式は重み$w_i$にも$\beta$が依存しているため,$\beta$について直接的に解くことはできませんが,仮に$w_i$が所与のもとでは,上の方程式は$\beta$について簡単に解くことができ,以下のような解になります.
\tilde{\beta}(w_1,\ldots,w_n)=\left(\sum_{i=1}^n w_i x_ix_i^\top \right)^{-1}\sum_{i=1}^n w_i x_iy_i
$\beta$の推定値が得られると$w_i$を計算することができるので,適当な初期値$\beta^{(0)}$から以下を収束するまで繰り返すことで,$\beta$を推定することができます.
- $\beta^{(s)}$を用いて重み$w_1^{(s)},\ldots,w_n^{(s)}$を計算
- $\beta^{(s+1)}=\tilde{\beta}(w_1^{(s)},\ldots,w_n^{(s)})$で$\beta$を更新
Tukeyの方法
$\psi(\cdot)$として以下のような関数を考えます.
\psi_C(x)=\begin{cases}
\frac{C^2}{6}\left[1-\left\{1-\left(\frac{x}{C}\right)^2\right\}^3\right] & (|x|<C) \\
\frac{C^2}{6} & (|x|\geq C)
\end{cases}
この関数はHuberの関数とは異なり,$|x|$が大きくなるにつれて関数の値が定数に収束します.したがって,$\sigma^{-1}|y_i-x_i^\top\beta|\geq C$となるデータ点の情報は$\beta$の推定に全く影響を与えません.これは,Huber型の関数と比べて外れ値の影響をより強く取り除く性質があることを意味しています.
この関数形に対してもHuberの方法と同様なIRLS法を用いて$\beta$を推定することが可能です.(詳細は割愛します.)
損失関数の形状
通常のOLSの損失関数と今回紹介したHuberとTukeyの方法における損失関数の形状をグラフとして以下に示しておきます.この図からそれぞれの損失関数の形状の違いがよくわかります.

適用例
HuberとTukeyの方法はそれぞれMASSパッケージのrlm関数を用いて実行することができます.
その際に$K$や$C$のチューニングパラメータの値を指定することも可能ですが,今回はデフォルトの値で実行します.また,$\sigma$の推定方法もオプションとして選択できますが,こちらもデフォルトの方法を今回は使います.
冒頭のケースAの例で両者を適用すると以下のような結果が得られます.

OLSは赤い点である外れ値に敏感なのに対し,HuberとTukeyの方法はそれぞれロバストな推定結果を与えていることがわかります.
最後に,上記の図を作成するために使ったRコードを以下に示しておきます.
# 擬似データの生成
set.seed(1)
n <- 50
x <- sort(rnorm(n, 0, 1)) # 説明変数
y <- x + 0.3*rnorm(n) # 被説明変数
sub <- (n-1):n
y[sub] <- y[sub] - 4
col <- rep(1, n)
col[sub] <- 2
# ロバスト回帰
library(MASS)
fit.Huber <- rlm(y~x, psi=psi.huber) # Huberの方法
fit.Tukey <- rlm(y~x, method="MM") # Tukeyの方法
# 結果の図示
par(mfcol=c(1,1))
plot(x, y, xlab="x", ylab="y", pch=20, col=col, cex=1.5)
abline(lm(y~x), col=1, lty=1)
abline(coef(fit.Huber), col="blue")
abline(coef(fit.Tukey), col="blue", lty=2)
legend("topleft", legend=c("OLS", "Huber", "Tukey"), col=c("black", "blue", "blue"), lty=c(1,1,2), lwd=1.5)
おわりに
今回は線形回帰モデルにおける外れ値とそのロバスト推定について紹介しました.
株式会社Nospareでは統計学の様々な分野を専門とする研究者が所属しております.統計アドバイザリーやビジネスデータの分析につきましては株式会社Nospareまでお問い合わせください.