東京大学・株式会社Nospareの菅澤です.
今回から「外れ値とロバスト推定」のテーマでいくつか記事を書いていこうと思います.
具体的には以下の内容について解説していく予定です.
- 一次元データの外れ値処理
- 多次元データおよび回帰モデルにおける外れ値とロバスト推定
- 一般的な統計モデルのロバスト推定 (ダイバージェンスの利用)
- ベイズ的なロバスト推定の方法
今回は「一次元データの外れ値処理」について解説していきます.
外れ値の存在
現実のデータには様々な要因(特異なサンプルの存在,入力ミス等)で外れ値が混入します.このような外れ値を適切に処理しなかった場合,本来求めたい結果とは大きく異なった結果が得られてしまう危険性があります.そのため,データを解析する前には外れ値の存在可能性について検討し,実際に(意味のない)外れ値が含まれる場合は適切に除去するなどの対策が必要になります.
平均値と中央値
下図は外れ値のある一次元のデータの例です.大部分のサンプルは正規分布に従っているように見えますが,15付近に大きな外れ値が複数存在していることが確認できます.
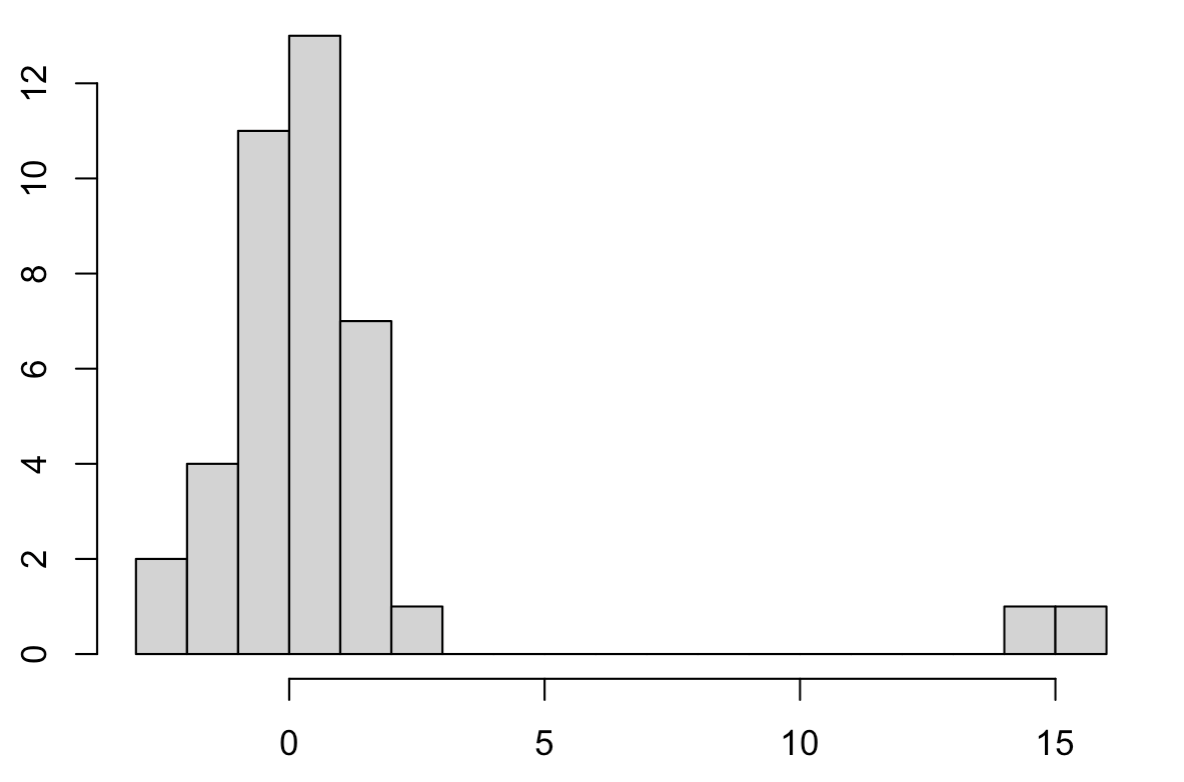
前提として,15付近にあるデータは意味のない(興味のない)サンプルで,解析から取り除きたい対象だとします.(外れ値をデータ解析から取り除くべきかはデータ解析の目的に依存することに注意してください.)
このような状況で単に標本平均を計算すると0.85になります.しかし,左側にまとまっているサンプルは原点付近を中心に分布しており,このデータの平均を表す要約統計量としては不適切な印象を受けます.これは標本平均が外れ値の影響を受けやすい統計量であることが原因です.
このような場合に外れ値に対してロバストに(頑健に)平均を推定する方法として,中央値を代わりに使うことができます.中央値はデータの中で順位が中央の値に相当します.中央値は順位の観点でデータを見ているので,外れ値の影響を受けにくい量になっています.実際に上の例で中央値を計算すると0.21となり,こちらの方が左の集団の平均を良く推定できていそうなことがわかります.
もちろん上のヒストグラムから容易に外れ値を特定することができるので,外れ値を除去したデータから標本平均を計算することもできます.その場合は0.12となり中央値と近い値になります.
外れ値の可視化
外れ値を手っ取り早く見つける方法はデータを可視化することです.先の例のようにヒストグラムを用いても良いですが,複数のデータを同時に可視化して外れ値をチェックするためには箱ひげ図が便利です.以下の図では,3つのデータに対して箱ひげ図を描いています.

箱ひげ図についている上下の「ヒゲ」はそれぞれ
- 下のヒゲ: (第一四分位数)-1.5×(四分位範囲) より大きいサンプルの最小値
- 上のヒゲ: (第三四分位数)+1.5×(四分位範囲) より小さいサンプルの最大値
を表します.ちなみに四分位範囲とは第三四分位数から第一四分位数を引いた値です.
Rで箱ひげ図を描くためのboxplot関数は,デフォルトの設定ではこのようなルールで「ヒゲ」が描かれ,上下のヒゲの間に含まれないデータは外れ値として表示されます.このように,箱ひげ図を用いることで外れ値が入っているか否かを複数の項目について同時に可視化することができます.
外れ値の自動検出
ヒストグラムや箱ひげ図によってデータを可視化することで簡単に外れ値を見つけられる場合がありますが,データの項目数(次元数)が多い場合にいちいち図を描いて確認して外れ値を除去する作業は面倒かもしれません.
もう少し機械的に外れ値を除去したい場合は,各サンプルが外れ値か否かを判定するルールを導入します.具体的な方法としては以下のような方法があります.
- (第一四分位数)-1.5×(四分位範囲)から(第三四分位数)+1.5×(四分位範囲)の範囲に入っていないサンプルは外れ値とする. (箱ひげ図で外れ値として表示する操作と同様.)
- (スミルノフ・グラブス検定) 「データから最も離れている値に対して以下のような統計量を計算 → ある閾値を超えたら外れ値とみなし取り除く」を繰り返し行う方法です.
\frac{X_o-\bar{X}}{\sqrt{S^2}}
($X_o$: 外れ値候補, $\bar{X}$: 標本平均, $S^2$: 標本分散)
一次元の外れ値検出だけでは不十分?
例として,以下の2つの箱ひげ図を見てみましょう.
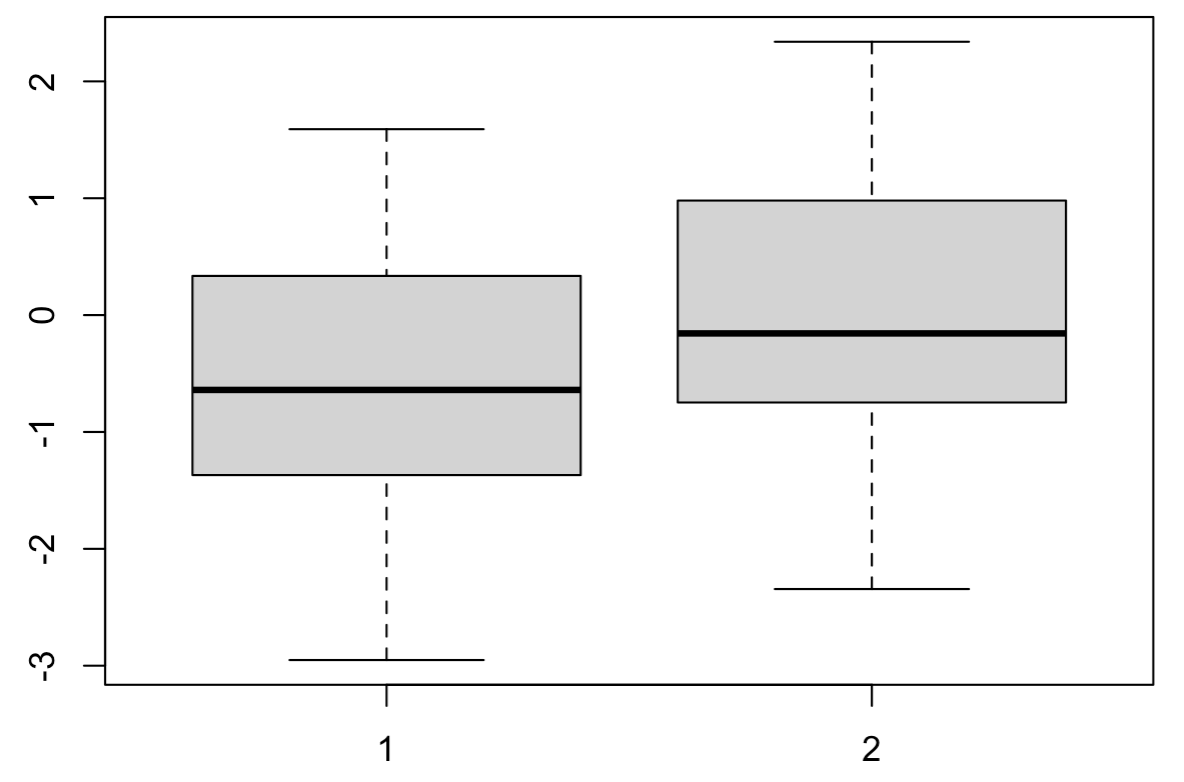
この図を見るとそれぞれの項目に外れ値は入っていない様に見えます.しかし,このデータを2次元のデータとしてプロットしてみたのが以下の図です.

**2次元のデータとして可視化してみると左上に2つ外れ値があることが確認できます.**各項目ごとの平均を推定する点では,この2つの外れ値はあまり影響を与えなさそうに思えますが,回帰モデルを適用する際には注視するべき外れ値になりそうです.このように,多次元のデータの場合は一次元でデータを眺めただけでは見えない外れ値が入っていることがあるので注意が必要です.
多次元のデータや回帰モデルにおける外れ値の処理については次回の記事で解説しようと思います.
おわりに
今回は一次元データの外れ値の処理方法について紹介しました.
株式会社Nospareでは統計学の様々な分野を専門とする研究者が所属しております.統計アドバイザリーやビジネスデータの分析につきましては株式会社Nospareまでお問い合わせください.
