最急降下法によるパラメータ最適化

はじめに

機械学習について学びたいと思い、CourseraのMachine Learningを始めたので復習を兼ねてアウトプットしていきたいと思います。

機械学習概要

最急降下法について説明する前に、機械学習の分類について触れておきます。
機械学習は大きく以下の3つに分類されます。

1. 教師あり学習(分類)

   • 説明変数を基に目的変数（カテゴリカル）を予測する
   • 例：花びらのサイズを基に花の種類を予測する

2. 教師あり学習(回帰)

   • 説明変数を基に目的変数（連続値を予測する）
   • 例：気温を基にアイスクリームの売り上げを予測する

3. 教師なし学習

   • 説明変数を基にデータを複数のグループに分類する
   • 例：動画の視聴履歴を基に利用者をグループ分けする

まだ教師なし学習の単元まで達していない(SVMで苦戦しています)ため、本投稿での話は全て教師あり学習の話だと捉えてください。

学習とは

いきなり核心に迫りますが機械学習（教師あり）における学習とは何でしょうか。答えを言ってしまうとこれはコスト関数の最小化であると思います。言い換えると、予測値と実測値の誤差を最小にするためにサンプルデータをよく説明できる直線を探すということになります。
数学的に言うと全てのデータは特定の式に従っているとみなし、全てのサンプルデータに対する誤差の合計が最小となる$\theta_0$～$\theta_m$を求めます。今回は線形回帰を例にとりました。ちなみに、$h_\theta(x)$の$h$はhypothesys(仮説）を表しています。
$$h_\theta(x) = \theta_0 + \theta_1x_1+...\theta_mx_m$$
あるサンプルに対する予測値と実測値の誤差は$h_\theta(x) - y$で表せるため、最小化したい関数は全てのサンプルに対する誤差の二乗平均の合計である以下の式となります。
$$J(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})^2$$
二乗されている理由は正負の値が混ざっていると誤差同士の打消しが発生してしまうためです。全体を割る数字が$\frac{1}{2}$ではなく$\frac{1}{2m}$となっている理由は後の微分に役立つからです。また、この関数のことをコスト関数といいます。
では、どのようにしてコスト関数の最小化を行えばよいでしょうか。方法はいろいろあるようですが、今回は最急降下法というのものを使用します。

最急降下法

最急降下法とはある関数の最小化を行う手法の一つで、関数をパラメータで偏微分することで関数の傾きを求め、少しずつ最小値に近づいていく手法です。実際にコスト関数をプロットしたものを見ていただけるとわかりやすいかと思いますが、その前に今回使用するデータを見てみます。なんとなく一次関数がフィットしそうです。

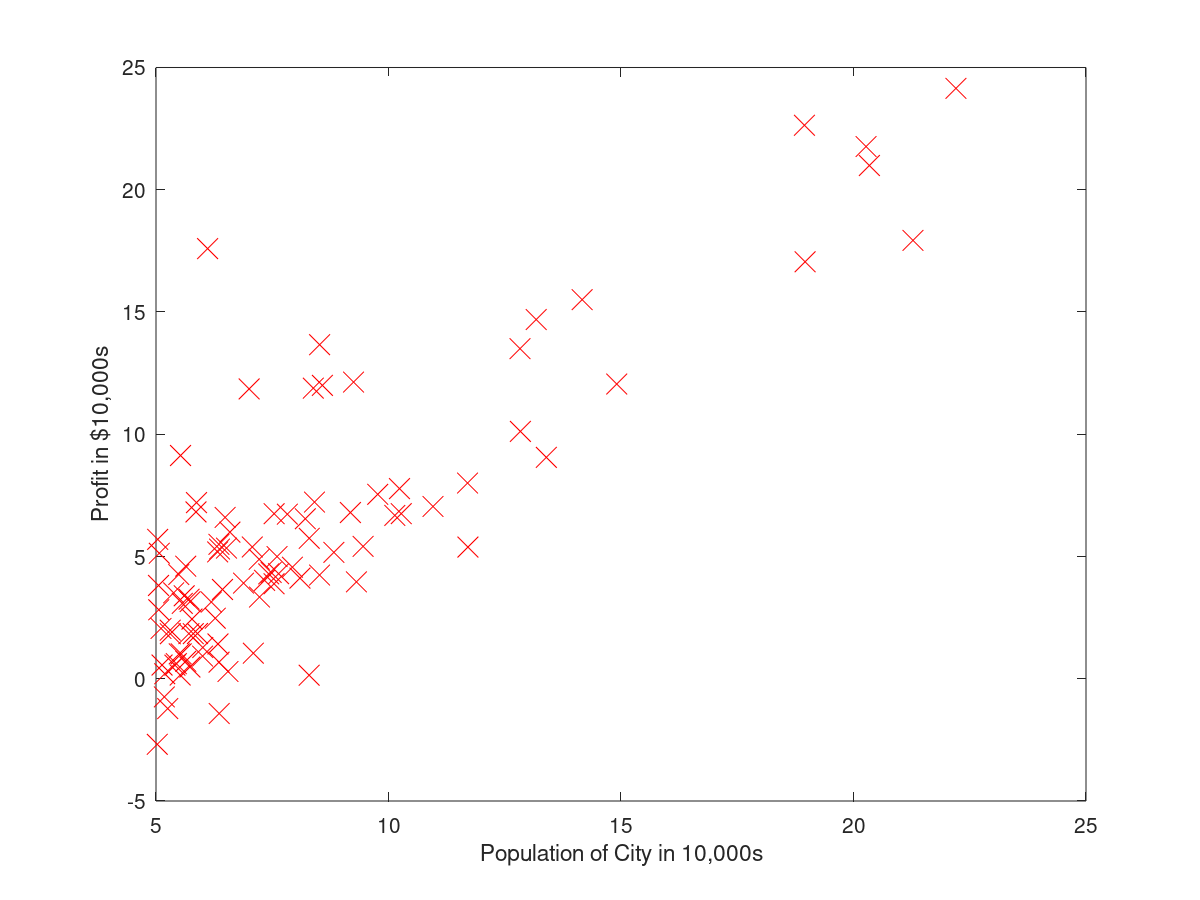
次にコスト関数をプロットしてみましょう。簡単化のため、$h_\theta(x)$は一次式とし、$\theta_0$は固定としました（$h_\theta(x) = 1 + \theta_1x_1$）。

1付近を最小値とする下向きの凸関数となっていることがわかります。現在の目的はコスト関数の最小化ですので、要はこの1付近の数字を見つけられればよいということになります。凸関数の最小値とは、言い換えれば傾きが0であるということですね。ということで、早速傾きが0になる地点を探してみましょう。傾きが0の地点は以下の方程式を解くことで見つけられます。
$$\frac{\partial}{\partial \theta_1}h_\theta(x) = 0$$
が、上の方法では式が複雑になったときや関数の形がわからない場合に最小値を見つけるのが難しくなるため、代わりに使うのが最急降下法です。
最急降下法では以下の作業を行うことで最小値に近づいていきます。

1. 適当な$\theta_1$を決める
2. $\theta_1$でコスト関数を偏微分し傾きを求める(傾き = $\frac{\partial}{\partial \theta_1}J(\theta)$)
3. 求めた傾きを使って$\theta_1$の更新を行う
4. 2にもどる

ではこれらの作業を行っていきましょう。

1. $\theta_1$の初期化
   これはなんでもいいので一先ず$\theta_1 = 0$としておきます。

2. コスト関数を$\theta_1$で偏微分し傾きを求める
   傾きは以下の式で求められます。
   $$h_\theta(x) = 1 + \theta_1x_1$$
   $$J(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})^2$$
   $$\frac{\partial}{\partial \theta_1}J(\theta) = \frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_1^{(i)}$$
   ここで再度コスト関数と$\theta_1$のプロットを見てみましょう。$\theta$は0で初期化されていますので、$\theta_1=0$の地点に注目します。

細かい数字も求められるのですが、ここでは正か負かだけに注目してください。$\theta_1=0$の地点では傾きが少しだけ負になっていることがわかります。この値を使用して$\theta_1$の更新を行います。 3. $\theta_1$の更新を行う 以下の式を使用して値の更新を行います。「:=」は代入するくらいに捉えてください。$\alpha$は学習率と呼ばれるもので任意の数字です。計算の簡単化のため、ここでは$\alpha = 1$とします。 $$\theta_1 := \theta_1 - \alpha\frac{\partial}{\partial \theta_1}J(\theta)$$ では更新式を読み取っていきましょう。現状を整理しておくと、以下のようになっています。 $$\theta_1 = 0$$ $$\alpha = 1$$ $$\frac{\partial}{\partial \theta_1}J(\theta) = 負の数$$ ここで先ほどの更新式を計算するとどうなるでしょうか。 $$\theta_1 := 0 - (1 * 負の数) = 正の数$$ となり、$\theta_1$が0から正の数に更新されました。図で言うと0から少し右側に移動したということになります。 4. 2にもどる 2、3の作業を何度も行うことで少しずつ最小値に近づいていきます。ここで、行き過ぎてしまった場合（最小値を超えて右側に行ってしまった場合）について考えてみます。仮に$\theta_1 = 2$の地点について考えると、$\frac{\partial}{\partial \theta_1}J(\theta)$は正の数となるので以下のようになります。 $$\theta_1 = 2$$ $$\alpha = 1$$ $$\frac{\partial}{\partial \theta_1}J(\theta) = 正の数$$ ここで先ほどの更新式を計算するとどうなるでしょうか。 $$\theta_1 := 2 - (1 * 正の数) = 2-正の数$$ ということで2よりもやや左側に移動することがわかります。このことから、$\theta_1$が最小値の右側にあろうが左側にあろうがいつかは収束することが期待できます。ちなみに、$\alpha$が大きすぎたり小さすぎたりすると収束しなかったり収束までのステップ数が多くなったりするのでこの辺りはデータによって変える必要があります。

このようにしてコスト関数を最小にするための$\theta_1$を求めることができました。先ほどは最適化を行う変数は$\theta_1$のみでしたが、$\theta_0$や$\theta_2$等の数が増えても行うことは変わりません。
$$J(\theta) = \theta_0 + \theta_1x_1 + \theta_2x_2$$
の場合は以下のようになります。
repeat until converge{
$$\theta_0 := \theta_0 - \alpha\frac{\partial}{\partial \theta_0}J(\theta)$$
$$\theta_1 := \theta_1 - \alpha\frac{\partial}{\partial \theta_1}J(\theta)$$
$$\theta_2 := \theta_2 - \alpha\frac{\partial}{\partial \theta_2}J(\theta)$$
}
本項の最初に貼ったデータに対し、$h_\theta(x) = \theta_0 + \theta_1x_1$をフィットさせたものが以下になります。それなりにフィットしてそうですね。コスト関数のグラフと照らし合わせてみると面白いかと思います。

まとめ

pythonやRを使えばこのような計算の中身を知らなくても実装することはできますし、学習率などのパラメータに関しても自動で見つけるパッケージはありますが中身を意識して実装することでより理解が深まるのかなと感じました。不定期にはなりますが、今後も復習を兼ねてアウトプットしていければと思います。

コード

octaveで実装した場合は以下のようになります。$X$も$\theta$も計算の効率化のためベクトル化されています。

for iter = 1:num_iters
    hx = X * theta;
    delta = 1 / m * X' * (hx - y);
    theta = theta - alpha * delta;
end