はじめに
2020年2月ごろ、金沢大学でとあるニュースが発表されました。
「世界最高精度・最高速度で点群位置合わせ問題の解を見つけるアルゴリズムを発見!」
https://www.kanazawa-u.ac.jp/rd/76252
https://github.com/ohirose/bcpd
Bayesian Coherent Point Drift、という革新的なアルゴリズムを発見したそうです。
このニューズをきっかけにCPDというアルゴリズムについて知りました。
知識のないド素人ですが、せっかくなので
CPD(coherent point drif)について勉強してみようと思います。
英語の翻訳が大変なので完全に個人的なメモ代わりに書いてます。
また、CPDの論文では剛体・非剛体の2つに対する手法が記載されているので
このシリーズではそれぞれに対する手法について勉強します。
このページでは、2つに共通する前提部分についての説明を行います。
点群の位置合わせ
https://arxiv.org/pdf/0905.2635.pdf
金沢大学のものを先に勉強したかったのですが、
まずはそれの基礎?になってると思われるCPDについて勉強します。
剛体の位置合わせについて。

ちょうどこの画像のようなイメージで位置合わせが行われます。
剛体の位置合わせは、基本的にはある点群に対して向きをあわせたあと、
平行移動、スケールの大きさが変更されることで、
2つの位置や大きさが異なる点群データを重なり合わせます。
実用例としては、例えば赤外線センサーで別々の場所から生成された点群を
1つの点群データに合体させたいときとかに使われます。
Open3DやPCLライブラリにあるICPはこれに該当します。
さて、本題のCoherent Point Drift。
CPDの場合は非剛体の点群を想定します。

図の赤い点と青い点の魚のように、形状が異なっている場合です。
このような形状の異なる点群の位置合わせを非剛体のレジストレーションと呼び、
CPDはこの非剛体のレジストレーションを想定します。
ただ、CPDの論文ではベースとして剛体のレジストレーションの手法について説明があったので、
このページでは勉強がてらまず剛体の手法について勉強します。
EMアルゴリズム
モデル
あるポイント$X$と、別のポイント$Y$があったとします。
それぞれの点群のポイント数が異なり、以下のようなポイントの集合をもっています。
X=(x_{1} \cdots x_{N}) \\
Y=(y_{1} \cdots y_{M}) \\
$Y$のポイントはGMMの重心、$X$のポイントはGMMによって生成されたデータとみなします。
さてこのとき、全確率の公式より以下の式が成立します。
p(x)=\sum_{m=1}^{M}P(m)p(x|m)
ここで、点群データがノイズや外れ値が存在する可能性を考慮して、
$p(x|M+1)=\frac{1}{N}$を混ぜ込むと以下の式となります。
p(x)=\sum_{m=1}^{M+1}P(m)p(x|m) \tag{1}
次に、尤度$p(x|m)$について考えます
ポイントxに対応する$Y$のポイントが$y_{m}$である確率。
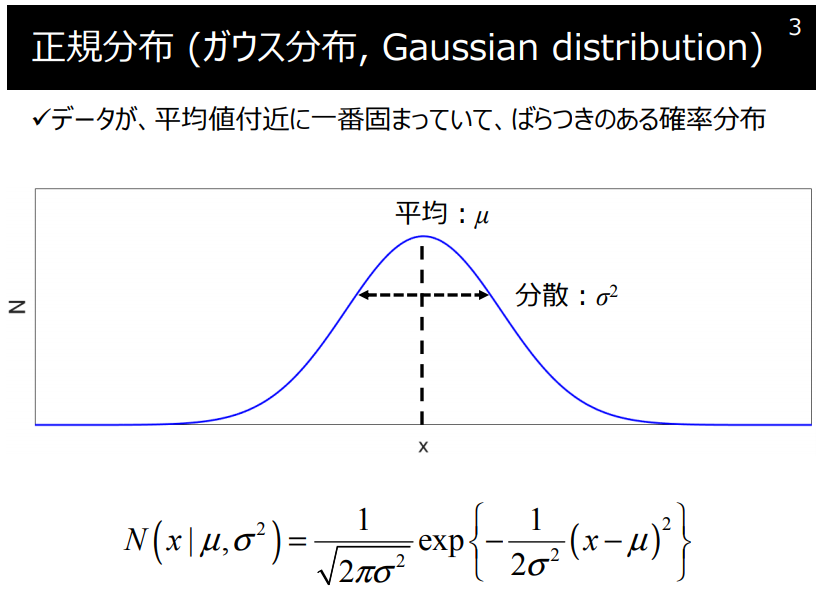
正規分布をもとに考えてみます。
https://datachemeng.com/wp-content/uploads/gaussianmixturemodel.pdf
ポイント$x$が$y_{m}$に対応するポイントであれば、
$p(x|m)$は$y_{m}$で確率が高くなるガウス分布になることが予想されます。
したがって、
p(x|m)=\frac{1}{(2\pi\sigma^{2})^\frac{D}{2}}exp^{-\frac{
\|x-y_{m}\|^{2}
}{2\sigma^{2}}} \tag{2}
事前確率$P(m)=\frac{1}{M}$について。
https://to-kei.net/bayes/noninformative_prior/
事前の情報がないので、無情報事前分布として一様分布とみなします。
P(m)=\frac{1}{M} \tag{3}
以上の情報より、(1)式を整理します。
p(x)=w\frac{1}{N} + (1-w)\sum_{m=1}^{M}\frac{1}{M}p(x|m)
さきほどノイズの存在を$p(x|M+1)=\frac{1}{N}$として定義しました。
これをΣから外に出したのが上式となります。
$w$はノイズ・外れ値を考慮した一様分布への重みです。
対数尤度関数
対数尤度関数$\log p(x|m)$を式で表します。
$x$は$x_{1}$...$x_{m}$の集合。それぞれのポイントは互いに影響を与えないので、
$P(A,B)=P(A)P(B)$のように積で表されます。したがって、$p(x|m)$は以下のようになります。
\log p(x|m)=\log \prod_{n=0}^Np(x_{n}|,m)\\
\log p(x|m)=\log (p(x_{1}|m)p(x_{2}|m)\cdots p(x_{n}|m)) \\
\log p(x|m)=\log p(x_{1}|m)+\log p(x_{2}|m)+\cdots +\log p(x_{n}|m)) \\
\log p(x|m)=\sum_{n=1}^{N}log\ p(x_{n}|m)\\
次に、条件付き確率の独立性について考えます。
事象AとBが互いに独立な事象なら、$P(A|B)=P(A)$となる性質があります。
すなわち、条件B下でのAの条件付き確率は、Aの「周辺確率」に等しくなります。
よって、$p(x|m)$は$p(x|m)=p(x)$とみなせます
したがって、(1)より先程の式は以下のように書き下されます。
\log p(x|m)=\sum_{n=1}^{N}log\ p(x_{n})\\
\log p(x|m)=\sum_{n=1}^{N}log\ \sum_{m=1}^{M}P(M+1)p(x|m)\\
logと総和、log-sumが式に含まれています。
log-sumは計算量が膨大で解析的に溶けないことで知られています。
この問題に対して有効なのがEMアルゴリズムです。
下界
まずは、EMアルゴリズムにおける下界を式にします。
条件付き確率と同時確率の関係式は以下の通りです。
p(x,m)=p(x|m)p(m)\\
この性質とイェンセンの方程式より、式を変形させて下界を求めます。
(参考:https://oimeg.blogspot.com/2015/07/em.html)
\log p(x|m)=\sum_{n=1}^{N}log\ \sum_{m=1}^{M+1}P(M)p(x|m)\\
\log p(x|m)=\sum_{n=1}^{N}log\ \sum_{m=1}^{M+1}p(x,m)\\
\log p(x|m)=\sum_{n=1}^{N}log\ \sum_{m=1}^{M+1}Q\frac{p(x,m)}{Q}\\
\log p(x|m)\ge\sum_{n=1}^{N} \sum_{m=1}^{M+1}Q\log \frac{p(x,m)}{Q}\\
このときの右辺が下界。これによりlog-sumはsum-logに解消されます。。
上式を見ると、上式の右辺と左辺は$\ge$で結ばれています。
sum-logの項を残して等式で表すには、
両辺の差「$\log p(x|m)-(下界)$」は何であるか求める必要があります。
結論から言えば、差分は$KL[Q|p(m|x)]$となります。
(参照:https://qiita.com/kenmatsu4/items/59ea3e5dfa3d4c161efb)
したがって、
\log p(x|m)=KL[Q|p(m|x)] + \sum_{n=1}^{N} \sum_{m=1}^{M+1}Q\log \frac{p(x,m)}{Q}\\
この式がEMアルゴリズムの基本となる式です。
この式をベースにEステップ、Mステップと実行します。
ここでのEMアルゴリズムは、パラメータ$θ$,$σ^{2}$を推定することです。
基本的な考え方としては、
・Eステップにて「古い」パラメータを推定し、
・Mステップでは「新しい」パラメータを発見する。
これを繰り替えすことで、真なるパラメータを求めます。
Eステップ
まずはEステップ。
パラメータを固定して$\log p(x|m)$を最大値化するQを考えます。
$\log p(x|m)$はQに依存しないので、Qをいくら変えてもそもそも変わりません。
そして、下界とは$\log p(x|m)$が取りうる最小値、下限です。
$\log p(x|m)$を最大値化しようと思えば、$\log p(x|m)$の下限は大きい必要があります。
したがって、mを固定して$\log p(x|m)$を最大値化するQを考えた場合に
$\log p(x|m)$が常に固定している状況で、下界を大きくしようと思えば、KLを最小化すればよいです。
KL divergenceとは、2つの確率の差異を図る尺度であり、
2つの確率が同じ場合には0となります。
したがって、$KL[Q|p(m|x)]$が0になるということは以下の式が成立します。
Q=p(m|x)\tag{4}
ここでのEステップの目的は、この事後確率を求めることに該当します。
事後確率の中身を詳しく式にしてみます。条件付き確率の性質より、以下の式を立てます。
p(m|x)=\frac{P(m)p(x|m)}{p(x)}
分母を整理します
(1)より、
p(x)=\sum_{m=1}^{M+1}P(m)p(x|m) \\
p(x)=\sum_{m=1}^{M}P(m)p(x|m)+P(M+1)p(x|M+1)
(2),(3)より
p(x)=\frac{1}{M}\sum_{m=1}^{M}
\left(
\frac{1}{(2\pi\sigma^{2})^\frac{D}{2}}exp^{-\frac{
\|x-y_{m}\|^{2}
}{2\sigma^{2}}}
\right)
+c
$c$は、$P(M+1)p(x|M+1)$は仮定した一様分布の掛け算なので定数です。
これにより分母を指揮にすることができたので、分子について(2)を代入すると
以下のように整理されます。
p^{old}(m|x)=\frac
{exp^{-\frac{
\|x-y_{m}\|^{2}
}{2\sigma^{2}}}}
{\sum_{m=1}^{M}
\left(
exp^{-\frac{
\|x-y_{m}\|^{2}
}{2\sigma^{2}}}
\right)
+c} \tag{5}
Eステップ、Mステップを実際に実行する際には、
パラメータを更新しながら繰り替えし処理が行われます。
Eステップでは、新しく求められたパラメータをもとに事後確率を計算します。
Mステップ
MステップではQを固定して、パラメータを最大化させます。
下界の式をもう一度みてます。下界は下記式の第二項にあたります。
\log p(x|m)=KL[Q|p(m|x)] + \sum_{n=1}^{N} \sum_{m=1}^{M+1}Q\log \frac{p(x,m)}{Q}\\
(4)より、下界にQを代入します。
\sum_{n=1}^{N} \sum_{m=1}^{M+1}Q\log \frac{p(x,m)}{Q}=\sum_{n=1}^{N} \sum_{m=1}^{M+1}p(m|x)\log \frac{p(x,m)}{p(m|x)}\\
=\sum_{n=1}^{N} \sum_{m=1}^{M+1}p(m|x)\log p(x,m) - \sum_{n=1}^{N} \sum_{m=1}^{M+1}p(m|x)\log p(m|x)\\
第一項をQ関数と呼びます。
また、第二項についてはパラメータに依存しないので定数とみなされます。
これにより、Q関数は以下のようになります。
Q(θ,σ^{2}) = \sum_{n=1}^{N} \sum_{m=1}^{M+1}p(m|x)\log p(x,m)\\
ここで、区別のために、$p(m|x)$をEステップに記載した$p^{old}(m|x)$で表記し直します。
Q(θ,σ^{2}) = \sum_{n=1}^{N} \sum_{m=1}^{M+1}p^{old}(m|x)\log p(x,m)\\
$p(x,m)$を条件付き確率で表します。
その前に・・・Mステップでの目的はパラメータの更新です。
新しいパラメータを条件付き確率をもちいて以下のように表します。
Q(θ,σ^{2}) = \sum_{n=1}^{N} \sum_{m=1}^{M+1}p^{old}(m|x)\log (p^{new}(x|m)p^{new}(m))
新しいパラメータは、このQ関数を最大化させることで計算されます。
M+1の項について。この項はノイズや外れ値を考慮して追加された項であり、
その分布は一様分布で定義されています。
Q関数においては定数として現れますが、Q関数を最大化する上では
定数は無視して良いので、以下のように再定義されます。
Q(θ,σ^{2}) = \sum_{n=1}^{N} \sum_{m=1}^{M}p^{old}(m|x)\log (p^{new}(x|m)p^{new}(m))\\
次に、$\log p_{new}(x|m)p_{new}(m)$について見てみます。
$\log p_{new}(x|m)p_{new}(m)$を以下のように展開します。
\log
\left(
p(x|m)p(m)
\right)=
\log
\frac{1}{M}
\left(
\frac{1}{(2\pi\sigma^{2})^\frac{D}{2}}exp^{-\frac{
\|x-y_{m}\|^{2}
}{2\sigma^{2}}}
\right)\\
\log (p(x|m)p(m))=const +
\log
\left(
M(2\pi\sigma^{2})^\frac{D}{2}
\right)
+
\log
\left(
exp^{-\frac{
\|x-y_{m}\|^{2}
}{2\sigma^{2}}}
\right)\\
\log (p(x|m)p(m))=const +
\frac{D}{2}
\log
\left(\sigma^{2}
\right)
+
{-\frac{
\|x-y_{m}\|^{2}
}{2\sigma^{2}}}
\\
これをQ関数に適用させます。
定数項を無視すると、以下のようになります。
Q(θ,σ^{2}) = \sum_{n=1}^{N} \sum_{m=1}^{M}p^{old}(m|x)\log (p^{new}(x|m)p^{new}(m))\\
Q(θ,σ^{2}) =
\sum_{n=1}^{N} \sum_{m=1}^{M}p^{old}(m|x)
\left(
\frac{D}{2}
\log
\left(\sigma^{2}
\right)
+
{-\frac{
\|x-y_{m}\|^{2}
}{2\sigma^{2}}}
\right)\\
Q(θ,σ^{2}) =
\sum_{n=1}^{N} \sum_{m=1}^{M}p^{old}(m|x)
\left(
\frac{D}{2}
\log
\left(\sigma^{2}
\right)
\right)
+
\sum_{n=1}^{N} \sum_{m=1}^{M}p^{old}(m|x)
\left(
{-\frac{
\|x-y_{m}\|^{2}
}{2\sigma^{2}}}
\right)\\
Q(θ,σ^{2}) =
\frac{N_{p}D}{2}
\log
\sigma^{2}
+
\frac{1}{2\sigma^{2}}
\sum_{n=1}^{N} \sum_{m=1}^{M}p^{old}(m|x)
\|x-y_{m}\|^{2}\\
したがって、Q関数は以下のように定義されます。
Q(θ,σ^{2}) =
\frac{N_{p}D}{2}
\log
\sigma^{2}
+
\frac{1}{2\sigma^{2}}
\sum_{n=1}^{N} \sum_{m=1}^{M}p^{old}(m|x)
\|x-y_{m}\|^{2}\\
\tag{6}
整理
求められた式を整理します。
Eステップでは(5)式が手に入りました。
p^{old}(m|x)=\frac
{exp^{-\frac{
\|x-y_{m}\|^{2}
}{2\sigma^{2}}}}
{\sum_{m=1}^{M}
\left(
exp^{-\frac{
\|x-y_{m}\|^{2}
}{2\sigma^{2}}}
\right)
+c} \tag{5}
Mステップでは(6)式が手に入りました。
Q(θ,σ^{2}) =
\frac{N_{p}D}{2}
\log
\sigma^{2}
+
\frac{1}{2\sigma^{2}}
\sum_{n=1}^{N} \sum_{m=1}^{M}p^{old}(m|x)
\|x-y_{m}\|^{2}\\
\tag{6}
これらの式を基本として、CPDの論文では
剛体、非剛体にたいするレジストレーションの手法を記載しています。
次回以降はここからどうするかを説明します。