環境
この記事は以下の環境で動いています。
| 項目 | 値 |
|---|---|
| CPU | Core i5-8250U |
| Ubuntu | 20.04 |
| ROS | Noetic |
インストールについてはROS講座02 インストールを参照してください。
またこの記事のプログラムはgithubにアップロードされています。ROS講座11 gitリポジトリを参照してください。
概要
2次元平面上の回転は1変数の角度$\theta$で表せますが、3次元空間上の回転は最低でも3要素が必要で表示形式も用途に合わせて何個かあり扱いが難しくなります。またROSで位置と姿勢を合わせたPoseの型がgeometry_msgの物とTFの物の2通りがあり使い分けが必要です。このページでは以下の4つのことについて説明します。
- 3次元の角度の表現方法とその例
- 3次元の角度の表現の変換方法とROSでの書き方
- ROSで位置姿勢を表す型
- ROSで位置姿勢を表す型の変換方法
3次元の角度の表現方式
オイラー(RPY)
表現
Yaw: Z方向の回転、Pitch: Y方向の回転、roll: X方向の3つのパラメーターで回転で表す形式です。例えば(10,20,30)とあったらZ軸で30度回した後に、新しくできたY軸で20度回して、新しくできたX軸で10度回します。このようにZ-Y-Xの順番で回します。注意ですが回る順番を変えると結果が変わってしまいます。特定の分野では順番が違ったりしますが、ロボットの世界ではこの順番がメジャーです。
その回転が何を表しているのかが人間が見て直感的にわかる反面、ジンバルロックという特異点や、軸の向きに強く影響されるのでコンピューター上の演算としては計算しにくいというデメリットがあります。
演算
RPY形式でそのまま計算することはできませんなので、通常は回転行列の形で計算することが多いです。
回転させる前の点を
v=
\left(
\begin{array}{ccc}
v_x\\
v_y\\
v_z
\end{array}
\right)\\
としたときにX、Y、Zのそれぞれの軸による回転は回転行列で
R_X(\theta)=
\left(
\begin{array}{ccc}
cos(\theta) & -sin(\theta) & 0 \\
sin(\theta) & cos(\theta) & 0 \\
0 & 0 & 1
\end{array}
\right)\\
R_Y(\theta)=
\left(
\begin{array}{ccc}
cos(\theta) & 0 & sin(\theta) \\
0 & 1 & 0 \\
-sin(\theta) & 0 & cos(\theta)
\end{array}
\right)\\
R_X(\theta)=
\left(
\begin{array}{ccc}
1 & 0 & 0\\
0 & cos(\theta) & -sin(\theta) \\
0 & sin(\theta) & cos(\theta)
\end{array}
\right)
と表せます。$RPY=(\theta_{yaw},\theta_{pitch},\theta_{roll})$で回転させた回転後のベクトルは
R_z(\theta_{yaw})R_y(\theta_{pitch})R_x(\theta_{roll})v
で表されます。各軸で回す順番が可換でないのと同じように、かける行列の順番も可換ではありません。
回転行列
表現
ベクトル$v=(vx, vy, vz)^T$があった時に目的の回転n回転を$Av$という結果になる回転です。
A=
\left(
\begin{array}{ccc}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}
\right)
のような9パラメーターで表現されますが以下の3つの条件(対象行列になる)
a_{12}=a_{21} \\
a_{13}=a_{31} \\
a_{23}=a_{32}
と以下の3つの条件(各列が直交する)
A1:=(a_{11},a_{12},a_{13})^T \\
A2:=(a_{21},a_{22},a_{23})^T \\
A3:=(a_{31},a_{32},a_{33})^T \\
\\
A1 \times A2=0 \\
A2 \times A3=0 \\
A3 \times A1=0
の6つの拘束条件が付くので実質は3自由度になります。複数の回転を1つにまとめる(下記)が簡単にできる反面、演算を長く行うと誤差が蓄積して上の拘束条件が緩くなり回転行列がゆがみ始めうることがデメリットとして挙げられます。
演算
上記で書いた通りです。例えばある2種類の回転を表す回転行列$A,B$があった場合にこの2つの回転を一気に行う回転行列は$AB$で求まります。
回転ベクトル(軸と回転角度)
表現
物理で出てくる形式です。$\omega=(1,0,0)$とあったらx軸周りに1[rad]回します。またこれの派生としてOpenGLで用いられる形式として$\omega=(1,0,0),\theta=90$のように単位ベクトルで表す回転軸と回転角度の組で表す方法もあります。微分が簡単にできることがメリットとして挙げられます。
演算
回転ベクトル表記で回転の計算をすることはできないので、回転行列か、四元数に変換して演算をします。また1回微分して速度になった時には回転速度ベクトルaとbの合成をa+bとして求められます。
四元数(クオータニオン)
表現
q=(w,x,y,z)と4つの数字で表す形式です。$|q|=\sqrt{w^2+x^2+y^2+z^2}=1$という拘束がありますので実質は3パラメーターです。q=(w,x,y,z)があった時にこれを虚数形式で$q=w+ix+jy+kz$と表します。四元数はこのようにベクトル表記と虚数表記の両方で表記することがあります。数学の世界では(w,x,y,z)の順に並べますが、コンピューターの世界やROSでは(x,y,z,w)の順番で表記します。
回転の計算がとてもしやすく4要素と少ない一方、人間から見ると直感的でないという問題があります。
回転軸を表す単位ベクトル$a=(a_x, a_y, a_z)$で、回転角度が$\theta$の場合は4元数は$(w,x,y,z)=(cos(\theta/2), a_x sin(\theta/2), a_y sin(\theta/2), a_z sin(\theta/2))$となります。
演算
虚数の計算は$ij=-ji=k, jk=-kj=i, ki=-ik=j, i^2=j^2=k^2=-1$となります。また$q=w+ix+jy+jz$に対してqの共役を$q'=w-ix-jy-jz$と定義します。回転する対象のベクトル$a=(0,a_x,a_y,a_z)=ia_x+ja_y+ka_z$とあった時に回転は$qaq'$と表します。
2種類の回転p,qがあった時にはその2つの回転の合成は$qpap'q'=qpa(qp)'$となります。
回転の補完
四元数のメリットとして以下のような簡単な式で2つの角度を滑らかに補完することができます。球上の弧を等速で進むような補完が出来ます。
\theta= \arccos(\frac{q1 \cdot q2}{|q1| \cdot |q2|}) \\
q=q1 \frac{\sin(1-t)\theta}{\sin \theta }+q2 \frac{\sin t \theta}{\sin \theta } (0<t<1)
まとめ
4つの方式をまとめます。
| 項目 | オイラー(RPY) | 回転行列 | 回転ベクトル | 四元数 |
|---|---|---|---|---|
| 計算のしやすさ | △ | 〇 | × | 〇 |
| 回転の合成 | × | 〇 | 〇 | △ |
| 直観的 | 〇 | × | 〇 | △ |
| おすすめ度 | △ | × | × | 〇 |
3次元の角度の表現方式の例
各々の方法で(1)0度回転(=回転なし)、(2)x軸90度回転、(3)y軸180度回転を例示します。
オイラー
(roll, pitch, yaw)でdegreeで表記
(1) $(0, 0, 0)$
(2) $(90, 0, 0)$
(3) $(0, 180, 0)$
回転行列
(1)
\left(
\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}
\right)
(2)
\left(
\begin{array}{ccc}
1 & 0 & 0 \\
0 & 0 & -1 \\
0 & 1 & 0
\end{array}
\right)
(3)
\left(
\begin{array}{ccc}
0 & 0 & 1 \\
0 & 1 & 0 \\
1 & 0 & 0
\end{array}
\right)
回転ベクトル
radianで表記
(1) $(0,0,0)$
(2) $(\pi/2,0,0)$
(3) $(0,\pi,0)$
4元数
(x,y,z,w)で表記
(1) $(0, 0, 0, 1)$
(2) $(\sqrt{1/2}, 0, 0, \sqrt{1/2})$
(3) $(0, 1, 0, 0)$
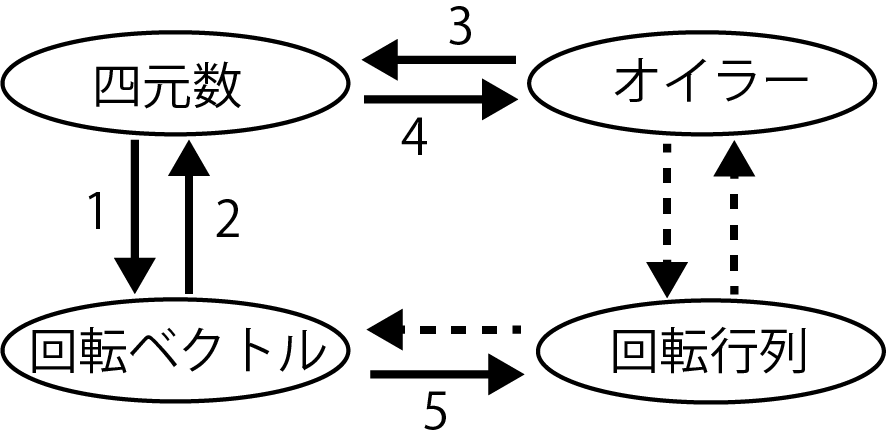
3次元の角度の表現方式の相互変換
相互変換の図を以下に載せます。$4 \times 3=12$通りの変換がありますが、変換が困難だったりほかの物を介して行うことが普通なものを除いて以下の5つを数式やソースコードを以下に解説していきます。
1.四元数->回転ベクトル
\left(
\begin{array}{ccc}
a_x \\
a_y \\
a_z
\end{array}
\right)
=
\left(
\begin{array}{ccc}
x/ \sqrt{1-w^2}\\
y/ \sqrt{1-w^2}\\
z/ \sqrt{1-w^2}\\
\end{array}
\right)
\\
\theta=2arctan(\frac{\sqrt{x^2+y^2+z^2}}{w})
2.回転ベクトル->4元数
これは簡単です。
\left(
\begin{array}{ccc}
w \\
x \\
y \\
z
\end{array}
\right)
=
\left(
\begin{array}{ccc}
cos(\theta/2) \\
a_x sin(\theta/2)\\
a_y sin(\theta/2)\\
a_z sin(\theta/2)\\
\end{array}
\right)
3.オイラー->四元数
式は四元数とオイラーの変換公式で記述されています。
ROSでは以下の関数を使います。
#include <geometry_msgs/Pose.h>
#include <tf/transform_broadcaster.h>
tf::Quaternion rpy_to_tf_quat(double roll, double pitch, double yaw){
return tf::createQuaternionFromRPY(roll, pitch, yaw);
}
geometry_msgs::Quaternion rpy_to_geometry_quat(double roll, double pitch, double yaw){
tf::Quaternion quat=tf::createQuaternionFromRPY(roll,pitch,yaw);
geometry_msgs::Quaternion geometry_quat;
quaternionTFToMsg(quat, geometry_quat);
return geometry_quat;
}
計算式を直接書くと以下のようになります。
void calc_quat_to_rpy(geometry_msgs::Quaternion geometry_quat, double& roll, double& pitch, double& yaw){
float q0q0 = geometry_quat.w * geometry_quat.w;
float q1q1 = geometry_quat.x * geometry_quat.x;
float q2q2 = geometry_quat.y * geometry_quat.y;
float q3q3 = geometry_quat.z * geometry_quat.z;
float q0q1 = geometry_quat.w * geometry_quat.x;
float q0q2 = geometry_quat.w * geometry_quat.y;
float q0q3 = geometry_quat.w * geometry_quat.z;
float q1q2 = geometry_quat.x * geometry_quat.y;
float q1q3 = geometry_quat.x * geometry_quat.z;
float q2q3 = geometry_quat.y * geometry_quat.z;
roll = atan2f((2.f * (q2q3 + q0q1)), (q0q0 - q1q1 - q2q2 + q3q3));
pitch = -asinf((2.f * (q1q3 - q0q2)));
yaw = atan2f((2.f * (q1q2 + q0q3)), (q0q0 + q1q1 - q2q2 - q3q3));
}
4.四元数->オイラー
式は四元数とオイラーの変換公式で記述されています。
ROSでは以下の関数を使います。
#include <geometry_msgs/Pose.h>
#include <tf/transform_broadcaster.h>
void tf_quat_to_rpy(double& roll, double& pitch, double& yaw, tf::Quaternion quat){
tf::Matrix3x3(quat).getRPY(roll, pitch, yaw); //rpy are Pass by Reference
}
void geometry_quat_to_rpy(double& roll, double& pitch, double& yaw, geometry_msgs::Quaternion geometry_quat){
tf::Quaternion quat;
quaternionMsgToTF(geometry_quat, quat);
tf::Matrix3x3(quat).getRPY(roll, pitch, yaw); //rpy are Pass by Reference
}
また計算式を直接書くと以下のようになります。
geometry_msgs::Quaternion calc_rpy_to_quat(double roll, double pitch, double yaw){
double cy = cos(yaw * 0.5);
double sy = sin(yaw * 0.5);
double cp = cos(pitch * 0.5);
double sp = sin(pitch * 0.5);
double cr = cos(roll * 0.5);
double sr = sin(roll * 0.5);
geometry_msgs::Quaternion q;
q.w = cr * cp * cy + sr * sp * sy;
q.x = sr * cp * cy - cr * sp * sy;
q.y = cr * sp * cy + sr * cp * sy;
q.z = cr * cp * sy - sr * sp * cy;
return q;
}
5.回転ベクトル->回転行列
ロドリゲスの公式といわれています。詳しくはロドリゲスの回転公式を見てください。
ROSで位置姿勢を表す型
3種類の型があります。
| 位置姿勢の型 | tf2:Transform | geometry_msgs::Pose | geometry_msgs::Transform |
|---|---|---|---|
| タイプ | c++の型 | ROSmsg | ROSmsg |
| 位置の型 | tf2::Vector3 | geometry_msgs/Point | geometry_msgs/Vector3 |
| 姿勢の型 | tf2::Quaternion | geometry_msgs/Quaternion | geometry_msgs/Quaternion |
tf2:Transformはtfの入出力で使われる型です。またtransform型では位置の連鎖や逆転などの操作が出来ます。
geometry_msgs/Transformはほとんど使われていません。
tf2:Transform型のアクセス
tf2::Transform setTF(float x, float y, float yaw){
tf2::Transform output;
tf2::Vector3 position(x, y, 0);
tf2::Quaternion orientation;
//tf2::Quaternion orientation(qx, qy, qz, qw);
orientation.setRPY(0, 0, yaw);
output.setOrigin(position);
output.setRotation(orientation);
return output;
}
void showTF(tf2::Transform tf){
double lx=tf.getOrigin().x();
double ly=tf.getOrigin().y();
double lz=tf.getOrigin().z();
double scale = sqrt(1 - tf.getRotation().getW() * tf.getRotation().getW());
double rx=tf.getRotation().getAxis().x() * scale;
double ry=tf.getRotation().getAxis().y() * scale;
double rz=tf.getRotation().getAxis().z() * scale;
double rw=tf.getRotation().getW();
printf("pos(x,y,z): %f, %f, %f\n", lx, ly, lz);
printf("ori(x,y,z,w): %f, %f, %f %f\n", rx, ry, rz, rw);
}
geometry_msgs/Pose型のアクセス
geometry_msgs::Pose setPose(float x, float y, float yaw){
geometry_msgs::Pose output;
output.position.x = x;
output.position.y = y;
output.position.z = 0;
output.orientation.x = 0;
output.orientation.y = 0;
output.orientation.z = sin(yaw / 2);
output.orientation.w = cos(yaw / 2);
return output;
}
void showPose(geometry_msgs::Pose msg){
printf("pos(x,y,z): %f, %f, %f\n", msg.position.x, msg.position.y, msg.position.z);
printf("ori(x,y,z,w): %f, %f, %f %f\n", msg.orientation.x, msg.orientation.y, msg.orientation.z, msg.orientation.w);
}
TF->Poseの変換
geometry_msgs::Pose convertTFToPose(tf2::Transform tf_data){
geometry_msgs::Pose pose;
tf2::convert(tf_data.getRotation(), pose.orientation);
pose.position.x = tf_data.getOrigin().getX();
pose.position.y = tf_data.getOrigin().getY();
pose.position.z = tf_data.getOrigin().getZ();
return pose;
}
Pose->TFの変換
tf2::Transform convertPoseToTF(geometry_msgs::Pose msg){
tf2::Transform tf_data;
tf2::convert(msg, tf_data);
return tf_data;
}
コメント
色々書いてきましたが、ROSは内部ではすべて4元数で扱っているので、わざわざ別表現を使うことはあまりないでしょう。4元数だと人間がわかりずらい時にオイラー角の表現に変換して人がデバッグをするぐらいです。
ROSの型としては基本的にgeometry_msgs::Poseを使い、適宜tf::transformを演算のために使うとよいでしょう。
参考
wikipedia: 回転行列
四元数と回転行列の変換
ロドリゲスの回転公式
四元数とオイラーの変換公式
四元数とオイラーの変換プログラム
四元数で球面線形補間
tf::transform
tf::transformの変換
Converting Datatypes