LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@spssfun2017(spss fun)inIBM

CPLEXサンプル OutSource（アウトソーシング、サプライヤー選択問題）を読み解く

Last updated at Posted at 2025-02-13

CPLEXのサンプルの Outsource（アウトソーシング ）を読み解いていきます。

オリジナルのサンプルは<サンプル導入ディレクトリ>examples/opl/models/Outsource
/outsource.mod
にあります。

  • 実行環境

    • CPLEX 22.1.1
    • Windows 11 64bit

  • サンプル
    この記事でのサンプルは、一部決定変数を集約してわかりやすくしています

□コード

□サンプルデータ

問題

３つの製品を３つのサプライヤーへ何個ずつ発注すればいいかを決定します。

  • サプライヤーごとに異なる割引タイプ(全ユニット割引または増分割引) で提供されます

    • 例えば、0-100個は単価100円、100－200個は単価90円で、150個発注する場合、割引タイプによって以下のように変わります
      • 全ユニット割引のサプライヤーは150個×90円＝13,500円
        image.png
      • 増分割引のサプライヤーは100個×100円+50個×90円=14,500円
        image.png

  • 各サプライヤーには、品目の総数に関する供給キャパシティーがあります

  • 目的は、最小コストで需要を満たすための、各サプライヤーへの各品目の発注数量を見つけることです。コストには、購入コストとセットアップ・コストが含まれます。セットアップ・コストは、そのサプライヤーに発注があれば発生します

{98CD0826-440E-4CCB-AB96-1890D797135E}.png

利用データ

1.各アイテム、各サプライヤーの数量レンジ毎の単価

image.png

2.サプライヤーの種類

サプライヤーの種類 サプライヤー
全ユニット割引のサプライヤー Supplier1,Supplier2
増分割引のサプライヤー Supplier3

3.アイテム毎の需要数

Items 値
Item1 150
Item2 150
Item3 120

4.各サプライヤーのセットアップコスト

Suppliers 値
Supplier1 20
Supplier2 30
Supplier3 10

5.各サプライヤーの全品目の供給能力

Suppliers 値
Supplier1 180
Supplier2 220
Supplier3 240

決定変数

  1. 各アイテム、各サプライヤーへの数量レンジ毎の発注量

目的関数

最小化：①購入と②セットアップコストの合計。一度でも発注をすればセットアップコストが発生する。

制約

  1. 各サプライヤーの供給能力以内
  2. 各アイテム需要量を満たす
  3. 全ユニット割引サプライヤーは、各品目に対して1つの価格レンジのみ
  4. 全ユニット割引サプライヤーは、数量に応じた正しい価格レンジの単価を適用する
  5. 増分割引サプライヤーは発注量に応じた数量レンジ内の数量の増分ごとに単価を適用する
  6. サプライヤーにいずれかのアイテムを発注すると、セットアップコストが発生します

問題の種類

整数計画

解

先に解を紹介します。

目的関数

①総発注コスト: 339.7
②総セットアップコスト: 60
=399.7

決定変数

1.各アイテム、各サプライヤーへの数量レンジ毎の発注量
{5A9FC81A-5C5F-4B52-B7DF-4D74FA392DE4}.png

OPLコード解説

OPLコードの解説を行っていきます。

利用データ

まず基本データの定義を行っています。

基本データ
{string} Items = ...;
{string} Suppliers = ...;
{string} AUDsuppliers = ...; // AUD（全単位割引）サプライヤー
{string} CQDsuppliers = ...; // CQD（増分割引）サプライヤー 

assert card(CQDsuppliers union AUDsuppliers) == card(Suppliers);

定義はoutsource_custom.datファイルの中で行っています。

基本データdat
Items = { Item1, Item2, Item3 };
Suppliers = { Supplier1, Supplier2, Supplier3 };
AUDsuppliers={ Supplier1, Supplier2  }; // AUD（全単位割引）サプライヤー
CQDsuppliers={ Supplier3}; // CQD（増分割引）サプライヤー

assertでSuppliersはAUDsuppliersとCQDsuppliersのUnion集合であることを検査しています。
違反している場合は以下のようなエラーになります。
image.png

次に人需要、供給能力、セットアップコストのデータ定義を行っています。

需要、供給能力、セットアップコスト
int ItemDemand[Items] = ...; // 品目ごとの需要数
int TotalSupplierCap[Suppliers] = ...; // 各サプライヤーの全品目の供給能力
int MaxN = sum(i in Suppliers) TotalSupplierCap[i];// 全供給能力

int SetupCost[Suppliers] = ...; // サプライヤー毎のセットアップコスト
需要、供給能力、セットアップコストdat
ItemDemand = [ 150, 150, 120 ]; // 品目ごとの需要数
TotalSupplierCap = [ 180, 220, 240 ]; // 各サプライヤーの全品目の供給能力

SetupCost=[20,30,10]; // サプライヤー毎のセットアップコスト

問題ブラウザで見ると以下のようになっています。
{9E1E7F6C-67B7-4A0C-A174-801888F499FD}.png

{BCEA04CB-D62D-411C-8458-87763F73FC4A}.png

{8B180F05-EC64-42FD-832F-4D4027A27E87}.png

次に数量レンジ毎の単価の定義を行っています。

数量レンジ毎の単価
int NumAmts = ...; // 数量レンジの数
range Amts = 1..NumAmts; // 数量レンジのインデックス
int BreakAmts[1..NumAmts+1] = ...; // 数量レンジ
float CostInRanges[Items][Suppliers][Amts] = ...; //数量レンジ毎の単価
数量レンジ毎の単価dat
NumAmts = 4; // 数量レンジの数
BreakAmts = [ 0, 100, 200, 500, 1000 ] ; // 数量レンジ

//数量レンジ毎の単価
CostInRanges = [ 
            //LT100, LT150, LT200, GT200
          [ [ .14, .13, .12 999.0]
            [ .04, .02, .02 .01 ]
            [ .14, .13, .12 999.0 ]
          ]
          [  
            [ 2.0, 1.5, 1.0 0.5]
            [ 2.2, 1.8, 0.9 0.4]
            [ 1.8, 1.7, 1.6 1.5]
          ]
          [       
            [ 3.0, 3.0, 1.0 0.5]
            [ 3.0, 2.0, 1.0 0.5]
            [ 1.2, 1.1, 0.9 0.5]
          ]  
         ];

問題ブラウザで見ると以下のようになっています。
数量レンジはループで使いたいため、インデックスで扱っています。
{DE592C0D-043E-4E9C-86A9-7CA85679E7FE}.png
数量レンジ毎の単価は縦持ちのデータになっています。数量レンジはインデックス(Amts)で表現されています。
{27B80A3A-2D07-4BE5-90B1-1C813926A374}.png

データは縦持ちですが、アイテムとサプライヤーのクロス表で表現すると以下のようになります。
image.png

決定変数

次に決定変数の定義を行っています。
dvarが決定変数を意味します。

決定変数１：各アイテム、各サプライヤーへの数量レンジ毎の発注量

各アイテム、各サプライヤーへの数量レンジ毎の発注量です。

各アイテム、各サプライヤーへの数量レンジ毎の発注量
dvar int Quantity[Items][Suppliers][Amts] in 0..MaxN;

これらの決定変数は、求められた解では以下のようになりました。

image.png

例えば、Item3のSupplier3の数量レンジ1(0-100個)で100個、と2(100-200)で20個を発注します。
データは縦持ちですが、アイテムとサプライヤーのクロス表で表現すると以下のようになります。

image.png

決定変数２：発注ありなしフラグ

テクニカルに定義した「各アイテム、各サプライヤーへの価格レンジ毎の発注のありなしフラグ」と「各サプライヤーへの発注のありなしフラグ」があります。決定変数Quantityから派生して、制約を表現するために使っています。

決定変数２-1：各アイテム、各サプライヤーへの価格レンジ毎の発注のありなしフラグ

発注ありなしフラグ
// 各アイテム、各サプライヤーへの価格レンジ毎の発注のありなしフラグ
dvar int SupAmt[Items][Suppliers][Amts] in 0..1;

求められた解では以下のようになりました。

image.png
例えば、Item3のSupplier3の数量レンジ1(0-100個)で100個、と2(100-200)で20個の発注があるのでフラグが立っています。

決定変数2-2：各サプライヤーへの発注のありなしフラグ

発注ありなしフラグ
// 各サプライヤーへの発注のありなしフラグ
dvar int Setup[Suppliers] in 0..1;

求められた解では以下のようになりました。
{188F7EE8-62BB-4FB8-BB6D-43CD8FC639F3}.png

全てのサプライヤーへの発注があったので、全てのサプライヤーにSetupのフラグが立っています。

目的関数

次に目的関数の定義を行っています。
「①総発注コスト」、「②総セットアップコスト」の合計です。それぞれを決定式で計算します。

①総発注コスト
dexpr float TotalVariableCost =
  sum(i in Items, s in Suppliers, a in Amts) CostInRanges[i][s][a] 
                                                 * Quantity[i][s][a];

図で表すと以下のようなイメージです。①総発注コストは合計で339.7です。
image.png

②総セットアップコスト
// ②総セットアップコスト
dexpr float TotalSetupCost =
  sum(s in Suppliers) SetupCost[s]*Setup[s];

図で表すと以下のようなイメージです。②総セットアップコストは合計で60です。
image.png

①と②を合わせた値を最小化します。

目的関数：①総発注コスト+②総セットアップコストの合計を最小化
minimize TotalVariableCost + TotalSetupCost;

制約

次に制約の定義を行っています。
subject toの中カッコで囲みます。

制約.mod
subject to{

---略----
}

制約1: 各サプライヤーの供給能力以内

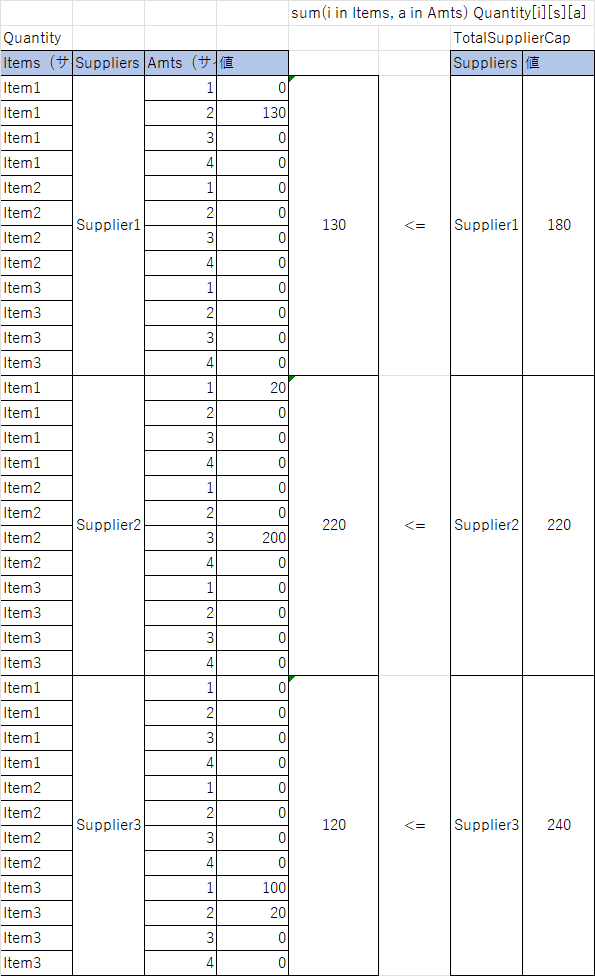
サプライヤー毎に発注数の合計をだして、 各サプライヤーの供給能以下であることを制約しています。

制約1:各サプライヤーの供給能力以内
  forall(s in Suppliers)
    ct01Caps: sum(i in Items, a in Amts) Quantity[i][s][a] <= TotalSupplierCap[s];

以下のような制約が定義されました（一部）。
{800C5E65-01BE-4E7C-8CEF-42956388C439}.png

図で表すと以下のようなイメージです。
image.png

制約２．各アイテム需要量を満たす

アイテム毎に発注数の合計をだして、 各アイテムの需要数以上であることを制約しています。

制約2:各アイテム需要量を満たす
  forall(i in Items)
    ct02Dem: sum(s in Suppliers, a in Amts) Quantity[i][s][a] >= ItemDemand[i];

以下のような制約が定義されました。
{A21382AF-F75F-4105-90B9-6E07193915CA}.png

図で表すと以下のようなイメージです。Item2の需要は150個ですが、200個発注しています。
これは150個の単価1.8と200個の単価0.9に大きな差があり、200個発注した方が安い((1.8*150個=270) > (0.9*200個=180))ためです。

image.png

制約３:全ユニット割引サプライヤーは、各品目に対して1つの価格レンジのみ

全ユニット割引サプライヤーは全量に同じ単価が適用されますので、アイテム×サプライヤーで1つの価格レンジであることが制約されます。0-100個のレンジと100－200個のレンジの両方への発注はできないという制約になっています。AUDsuppliersのみが対象なのでSupplier3は対象外です。

制約３:全ユニット割引サプライヤーは、各品目に対して1つの価格レンジのみ
  forall(i in Items, s in AUDsuppliers)
    ct03:
    sum(a in Amts) SupAmt[i][s][a] == 1;

以下のような制約が定義されました。
{C51AEE3B-B98F-4C80-A1EA-14B5EBA03290}.png

図で表すと以下のようになります。
image.png

制約４:全ユニット割引サプライヤーは、発注量に応じた正しい価格レンジの単価を適用する

二つの制約からなります。
全ユニット割引サプライヤーだけの制約なので、AUDsuppliersが対象になっています。

制約4_1:ある数量レンジの発注量は、その次数量レンジの数量-1以下になる

例えば、100－200個のレンジ内の数量の発注は199個以下に制約する必要があります。
BreakAmts[a+1]で次のレンジの数量を取り出しています。そしてこれにそのレンジへの発注があるかのフラグSupAmt[i][s][a]をかけて<=の比較を可能にしています。発注がなければSupAmt[i][s][a]が0になり、0<=0で比較をキャンセルしています。

制約4_1:ある数量レンジの発注量は、その次数量レンジの数量-1以下になる
  forall(i in Items, s in AUDsuppliers, a in Amts) {
    ct04_1:
    Quantity[i][s][a] <= (BreakAmts[a+1]-1) * SupAmt[i][s][a];
  }

以下のような制約が定義されました。
{18452229-CF8F-40AD-8B87-F1F47D323BB0}.png

図で表すと以下のようになります。
例えば、Supplier１に対するItem1の発注は130個です。これは100－200個のレンジ内の数量の発注なので、199個以下に制約されています。
image.png

制約4_2:ある数量レンジの発注量は、数量レンジの数量以上になる

例えば、100－200個のレンジ内の数量の発注は100個以上に制約する必要があります。
BreakAmts[a]でそのレンジの数量を取り出しています。そしてこれにそのレンジへの発注があるかのフラグSupAmt[i][s][a]をかけて>=の比較を可能にしています。発注がなければSupAmt[i][s][a]が0になり、0>=0で比較をキャンセルしています。

制約4_2:ある数量レンジの発注量は、数量レンジの数量以上になる
  forall(i in Items, s in AUDsuppliers, a in Amts) {
    ct04_2:
    Quantity[i][s][a] >= (BreakAmts[a]) * SupAmt[i][s][a];
  }

以下のような制約が定義されました。
{9A4D9AE1-27E9-4721-89D6-4ADA8653A618}.png

図で表すと以下のようになります。
例えば、Supplier１に対するItem1の発注は130個です。これは100－200個のレンジ内の数量の発注なので、100個以上に制約しています。
image.png

制約５:増分割引サプライヤーは発注量に応じた数量レンジ内の数量の増分ごとの単価を適用する

増分割引サプライヤーに、例えば120個の発注する場合、0-100個のレンジに対する100個の発注と、100－200個レンジに対する20個の発注とに分ける必要があります。これを制約で表現します。この制約がこの問題で最も難しいところです。

二つの制約からなります。
増分割引サプライヤーだけの制約なので、CQDsuppliersが対象になっています。

制約5_1:ある数量レンジを超える発注量がある場合は、それ以下の数量レンジへの発注数は、各数量レンジ区間の数量になる

forall(i in Items, s in CQDsuppliers, a in Amts)のループの中にforall(k in 1..a-1)があります。
なので
a=1: kはなし
a=2: k=1
a=3: K=1,2
a=4: K=1,2,3
でループします。
aはSupAmt[i][s][a]で使われています。SupAmt[i][s][a]はその価格レンジに発注があったかを示すフラグです。これを用いて、例えば、a=3:「200-500個」のレンジに発注があった場合は、k=1:「0-100個」のレンジとk=2:「100-200個」のレンジに発注があるかをこのループでチェックしています。

(BreakAmts[k+1]-BreakAmts[k])は上位レンジと下位レンジの個数差、つまりそのレンジの最大個数を示しています。例えばk=2の場合、200(BreakAmts[2+1])-100(BreakAmts[2])=100、つまり100－200個のレンジには100個発注が可能ということになります。

制約5_1:ある数量レンジを超える発注量がある場合は、それ以下の数量レンジへの発注数は、各数量レンジ区間の数量になる
  forall(i in Items, s in CQDsuppliers, a in Amts) {
    ct05_1:
    forall(k in 1..a-1) {
      Quantity[i][s][k] >= (BreakAmts[k+1]-BreakAmts[k])*SupAmt[i][s][a];
    }
  }

以下のような制約が定義されました（この表示には誤りがあり、Item3が表示されていません）。
image.png

図で表すと以下のようになります。
例えば、Supplier3に対するItem3の発注は120個です。これはa=2:「100－200個」のレンジ内の数量の発注が存在するので、一つ前のk=1:「0－100個」の発注量が100個以上（制約5_2で「0－100個の発注量が100個以下」を定義しているので、実質は==100）に制約されています。
そして、120個の発注は、a=3:「200－500個」のレンジ内の数量には存在ありませんので、一つ前のk=2:「100－200個」の発注量はすべて満たす必要がないため、20>=0の式で評価されています。
image.png

制約5_2:各数量範囲の発注量は、数量レンジ区間の数量以下である

SupAmt[i][s][a]で発注のあるレンジかどうかをチェックして、発注のあるレンジについてはそのレンジ範囲の数量以下の数量であることを制約しています。

(BreakAmts[a+1]-BreakAmts[a])は上位レンジと下位レンジの個数差、つまりそのレンジの最大個数を示しています。例えばa=2の場合、200(BreakAmts[2+1])-100(BreakAmts[2])=100、つまり100－200個のレンジには100個発注が可能ということになります。

制約5_2:各数量範囲の発注量は、数量レンジ区間の数量以下である
  forall(i in Items, s in CQDsuppliers, a in Amts) {
    ct05_2:
    Quantity[i][s][a] <= (BreakAmts[a+1]-BreakAmts[a])*SupAmt[i][s][a]; 
  }

以下のような制約が定義されました。
{24845983-FA32-4DD7-A741-A6ECFD9EB0DA}.png

図で表すと以下のようになります。
例えば、Supplier3に対するItem3の発注は120個です。0－100個の発注量が100個以下で100<=100、100－200個の発注量が100個以下で20<=100が制約されています。
一方で、Item1とItem2の0－100個のQuantityは0で発注がないのに、SupAmtに1が立っています。SupAmtは発注があることを示すフラグなので、本来は0であるべきです。ただ、0<=100は成り立ち、決定変数Quantityとしては正しい解が得られていますので無視します。
image.png

制約６:サプライヤーにいずれかのアイテムを発注すると、セットアップコストが発生する

sum(i in Items, a in Amts) Quantity[i][s][a]で各サプライヤーへの総発注量を算出しています。
MaxNは全サプライヤーの供給能力の合計なので、各サプライヤーへの発注はこれを超えることはありません。
仮に、あるサプライヤーの発注がある場合、Setup[s]を1にしないとこの不等式が成り立ちません。逆に言うとサプライヤーの発注が0の場合は、Setup[s]が0になります。

制約６:サプライヤーにいずれかのアイテムを発注すると、セットアップコストが発生する
  forall(s in Suppliers) 
    ct06Setup: Setup[s]*MaxN >= sum(i in Items, a in Amts) Quantity[i][s][a];

以下のような制約が定義されました。
{68749BB3-80E9-4258-B6A1-BE8ADB3E78B5}.png

図で表すと以下のようになります。
全てのサプライヤーで発注があったので、Setupも1になっています。
image.png

結果サマリー表示

最後にアイテムとサプライヤーの発注量をサマリーして表示します。
sum(a in Amts)(Quantity[i][s][a])で価格レンジに分かれていた発注を合計しています。

発注サマリー表示
int TotalQuantity[i in Items][s in Suppliers] = sum(a in Amts)(Quantity[i][s][a]);

execute DISPLAY {
   writeln("TotalQuantity = ", TotalQuantity);
}

以下のように算出されました。
{BF8CE50F-97BE-493E-8E95-6DC0BE7E84F1}.png
スクリプト・ログには以下のように出力されます。
{117FE132-3A75-40FF-945F-04ADBAC5FE3A}.png

完成OPL

製品サンプルとほぼ同じ内容ですが、日本語コメントを入れたり順序を入れ替えたり、添え字を入れ替えたりして読みやすくしています。

outsource_custom2.mod
{string} Items = ...;
{string} Suppliers = ...;
{string} AUDsuppliers = ...; // AUD（全単位割引）サプライヤー
{string} CQDsuppliers = ...; // CQD（増分割引）サプライヤー 

assert card(CQDsuppliers union AUDsuppliers) == card(Suppliers);

int ItemDemand[Items] = ...; // 各アイテムの需要数
int TotalSupplierCap[Suppliers] = ...; // 各サプライヤーの全品目の供給能力
int MaxN = sum(i in Suppliers) TotalSupplierCap[i];// 全供給能力

int SetupCost[Suppliers] = ...; // サプライヤー毎のセットアップコスト

int NumAmts = ...; // 数量レンジの数
range Amts = 1..NumAmts; // 数量レンジのインデックス
int BreakAmts[1..NumAmts+1] = ...; // 数量レンジ
float CostInRanges[Items][Suppliers][Amts] = ...; //数量レンジ毎の単価



// 決定変数
// 各アイテム、各サプライヤーへの数量レンジ毎の発注量
dvar int Quantity[Items][Suppliers][Amts] in 0..MaxN;
// 各アイテム、各サプライヤーへの価格レンジ毎の発注のありなしフラグ
dvar int SupAmt[Items][Suppliers][Amts] in 0..1;
// 各サプライヤーへの発注のありなしフラグ
dvar int Setup[Suppliers] in 0..1;

// 決定式
// ①総発注コスト
dexpr float TotalVariableCost =
  sum(i in Items, s in Suppliers, a in Amts) CostInRanges[i][s][a] 
                                                 * Quantity[i][s][a];
// ②総セットアップコスト
dexpr float TotalSetupCost =
  sum(s in Suppliers) SetupCost[s]*Setup[s];                                            


// 目的関数：①総発注コスト+②総セットアップコストの合計を最小化
minimize TotalVariableCost + TotalSetupCost;

// 制約                                              
subject to {
  // 各サプライヤーの供給能力以内
  forall(s in Suppliers)
    ct01Caps: sum(i in Items, a in Amts) Quantity[i][s][a] <= TotalSupplierCap[s];
       
  // 各アイテム需要量を満たす
  forall(i in Items)
    ct02Dem: sum(s in Suppliers, a in Amts) Quantity[i][s][a] >= ItemDemand[i];
      
  // 全ユニット割引サプライヤーは、各品目に対して1つの価格レンジのみ
  forall(i in Items, s in AUDsuppliers)
    ct03:
    sum(a in Amts) SupAmt[i][s][a] == 1;
        
  // 全ユニット割引サプライヤーは、発注量に応じた正しい価格レンジの単価を適用する
  forall(i in Items, s in AUDsuppliers, a in Amts) {
    // ある数量レンジの発注量は、その次数量レンジの数量-1以下になる
    // 例えば、100－200個のレンジ内の数量の発注は199個以下。
    ct04_1:
    Quantity[i][s][a] <= (BreakAmts[a+1]-1) * SupAmt[i][s][a];
    // ある数量レンジの発注量は、数量レンジの数量以上になる
   // 例えば、100－200個のレンジ内の数量の発注は100個以上。
    ct04_2:
    Quantity[i][s][a] >= (BreakAmts[a]) * SupAmt[i][s][a];
  }
   
  //増分割引サプライヤーは発注量に応じた数量レンジ内の数量の増分ごとの単価を適用する
  forall(i in Items, s in CQDsuppliers, a in Amts) {
    ct05_1:
    forall(k in 1..a-1) {
      // ある数量レンジを超える発注量がある場合は、それ以下の数量レンジへの発注数は、各数量レンジ区間の数量になる
      // 例えば、0-100個は単価100円、100－200個は単価90円で、150個発注する場合、0-100個のレンジに対する発注は100個になる。
      // Because the "quantity" for CQDs is incremental, if CQD order quantity lies 
      // in discount interval a, namely, sup[i,s,a]=1, then
      // the quantities in interval 1 to a-1, should be the length of those ranges.  
      Quantity[i][s][k] >= (BreakAmts[k+1]-BreakAmts[k])*SupAmt[i][s][a];      
    }
    // 各数量範囲の発注量は、数量レンジ区間の数量以下である      
    ct05_2:
    Quantity[i][s][a] <= (BreakAmts[a+1]-BreakAmts[a])*SupAmt[i][s][a];            
  }


  //サプライヤーにいずれかのアイテムを発注すると、セットアップコストが発生する
  forall(s in Suppliers) 
    ct06Setup: Setup[s]*MaxN >= sum(i in Items, a in Amts) Quantity[i][s][a];

}

//発注サマリー表示
int TotalQuantity[i in Items][s in Suppliers] = sum(a in Amts)(Quantity[i][s][a]);

execute DISPLAY {
   writeln("TotalQuantity = ", TotalQuantity);
}

データは以下です。

outsource_custom.dat
Items = { Item1, Item2, Item3 };
Suppliers = { Supplier1, Supplier2, Supplier3 };
AUDsuppliers={ Supplier1, Supplier2  }; // AUD（全単位割引）サプライヤー
CQDsuppliers={ Supplier3}; // CQD（増分割引）サプライヤー 

ItemDemand = [ 150, 150, 120 ]; // 品目ごとの需要数
//ItemDemand = [ 200, 150, 250 ];
TotalSupplierCap = [ 180, 220, 240 ]; // 各サプライヤーの全品目の供給能力
//TotalSupplierCap = [ 180, 220, 300 ];

SetupCost=[20,30,10]; // サプライヤー毎のセットアップコスト

NumAmts = 4; // 数量レンジの数
BreakAmts = [ 0, 100, 200, 500, 1000 ] ; // 数量レンジ

//数量レンジ毎の単価
CostInRanges = [ 
            //LT100, LT150, LT200, GT200
          [ [ .14, .13, .12 999.0]
            [ .04, .02, .02 .01 ]
            [ .14, .13, .12 999.0 ]
          ]
          [  
            [ 2.0, 1.5, 1.0 0.5]
            [ 2.2, 1.8, 0.9 0.4]
            [ 1.8, 1.7, 1.6 1.5]
          ]
          [       
            [ 3.0, 3.0, 1.0 0.5]
            [ 3.0, 2.0, 1.0 0.5]
            [ 1.2, 1.1, 0.9 0.5]
          ]  
         ];

参考

アウトソーシング - IBM Documentation

CPLEXサンプルを読み解く記事一覧

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?